黄冈市近四年中考二次函数压轴题的解题研究
杨媛媛,吴卫兵
(黄冈师范学院 数理学院,湖北 黄州 438000)
黄冈市近四年中考二次函数压轴题的解题研究
杨媛媛,吴卫兵
(黄冈师范学院 数理学院,湖北 黄州 438000)
本文分析了黄冈市近四年中考数学二次函数压轴题,在分析总结二次函数压轴题的特点上,以函数上的动点为核心,对这类题型进行了分类讨论,并针对不同类型给出了相应的解题思路和方法,最后对二次函数压轴题的解题思路进行归纳总结。
中考题;二次函数;抛物线;解题研究
每年中考的二次函数压轴题都体现着中考的命题趋势和特点,纵观黄冈市近几年的中考试题,不难发现最后的二次函数压轴题都趋向于动态问题的研究,黄冈市中考数学试题历年来在压轴题上都注重对学生基础及能力的考查,同时也很好的把握了试题的区分度,在基础和能力上做到并重,让不同的学生得到不同的发展,总之,压轴题的内容与结构充分体现了综合性、可选择性与均衡性,完全符合新课标的要求[1]。在新课标中,考试内容改革要求各科命题要注重考查学生运用知识分析问题、解决问题的能力,这样更有利于发挥学生的创造性。数学考试应在考查学生基本运算能力、思维能力和空间观念的同时,着重考查学生运用数学知识分析和解决简单实际问题的能力。
1 二次函数压轴题的特点
二次函数作为初中数学教学的重点内容,成为备受师生关注的热点问题。初中数学的二次函数教学的目的主要是培养学生数形结合、化归、方程及函数等重要数学思想,对于二次函数压轴题,应该从多角度、多层次去看待题目,要深入挖掘题目中的内在联系、辨别条件、结论之间的关联,确定该题目的类型,从而更好地确定解题思路。针对黄冈市近四年中考二次函数的压轴题的研究,发现了以下特点。
首先,尽管二次函数压轴题型多种多样,但是其重点仍然是考察二次函数的基础知识与内涵。因此,需要熟练掌握二次函数的数形特点、平移、变换等法则。
其次,二次函数压轴题越来越注重与几何图形的结合,更强调数形结合的思想,综合性越来越强。
再者,二次函数压轴题加强了对学生思维能力的考察。二次函数压轴题要求学生具备问题探究、信息获取、空间想象、综合分析等多种能力,充分体现了新课改下数学的特点。
最后,中考二次函数压轴题加强了数学问题与工程应用、生活实际问题相结合,具体化抽象,将实际问题数学化,让学生充分感受到数学与生活的联系[2]。
2 二次函数压轴题类型的归纳与分析
在初中数学中与“运动、变化”有关问题一般都是教学中的难点,新课程实施以来,降低了平面几何论证的要求,以纯几何为背景的压轴题,是近几年来中考压轴题的一种重要题型。这类试题能将代数与几何的众多知识有效整合,能有效考察学生分析问题和解决问题的能力,较好的渗透分类讨论、数形结合、化归等数学思想[3]。本文以黄冈市近四年的中考二次函数压轴题为例进行分析。
2.1 动点与直线相结合

(1)求经过A、B、C三点的抛物线的解析式;
(2)当点Q在CO边上运动时,求ΔOPQ的面积S与时间t的函数关系式;
(3)以O、P、Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值,若不能,请说明理由;
(4)经过A、B、C三点的抛物线的对称轴、直线OB和PQ能够交于一点吗?若能,请求出此时t的值(或范围),若不能,请说明理由。
分析:2013年第(4)问中,证明三线是否交于一点,以及在2015年中考卷第(3)问中求t值使得OP=PQ均为动点与直线相结合的问题。针对此类问题,可按以下思路来解决:
首先,化动为静,分析动点的轨迹,确定其坐标,以及变量的范围;
其次,再根据题目要求的结果进行逆推思想,像2013年第(4)问根据三线交于一点的性质先将其中两条线的表达式求解出来,然后联立方程求出交点;
后代入另一个方程中,看是否能求出满足条件的变量。
第(4)问要说明三线是否交于一点,在此题所给的条件下,本文首先要求出抛物线的对称轴,然后易于求出直线OB解析式,先假设三线交于一点,则可以利用抛物线的对称轴和直线OB的解析式求出它们的交点坐标,设为M,由于点Q和点P都是动点,为了确定它们的解析式,则利用假设三线交于点M的条件,用顶点M和动点P列出PM的解析式,最后根据点Q运动的两种情况分别将其坐标代入解析式,若能解出与条件相符合的t,则说明三线能交于一点,若这样的不存在则说明三线不能交于一点。
例题2:在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将ΔBCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系。(2015黄冈市,24题,如图2所示。)
(1)求OE的长。
(2)求经过O,D,C三点的抛物线的解析式;
(3)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动。设运动时间为t秒,当t为何值时,DP=DQ;
(4)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标,若不存在,请说明理由。
分析:2015年第(3)问涉及到抛物线的动点问题需要用以动化静的方法来解决。则要用变量分别表示出两条线段,然后联立方程求出变量。具体思路如下:

方法二:这种方法计算上比较简单,在思维上要求高一点,根据题目给出的折叠条件,可以结合DP=DQ证出RtΔDBP≅RtDEQ(HL)(这里要求学生掌握三角形全等的运用),由此我们可以得出BP=EQ,然后根据二者有关t的表达式解出t的值。
评析:上述2例题主要考查抛物线的综合应用,涉及待定系数法、全等三角形的判定和性质、折叠的性质、平行四边形的性质等知识点。考查动点与直线相结合为主,考查知识点较多,综合性较强,难度适中。
2.2 动点与几何图形相结合
2.2.1 动点与三角形相结合
(1)求点A,点B,点C的坐标;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;
(4)在点P的运动过程中,是否存在点Q,使ΔBDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由。
2013年第(3)问和2016年第(4)问均涉及到了动点与三角形相结合的问题,针对此类问题,解题思路如下:首先根据动点的运动轨迹,确定动点的运动范围以及动点的坐标,然后再根据题目所给的直角三角形的性质利用方程思想求解。如2013年和2016年中给出的都是直角三角形,那么利用变量将三边表示出来利用勾股定理即可求解,在此类问题中需要注意的是动点运动的轨迹以及变量的范围问题。
评析:上述2例题主要考查二次函数与三角形结合,该题型主要考查学生的基本功,三角形是几何证明和解析的基础,通过将一次函数、二次函数、一元二次方程灵活地同相似三角形、直角三角形、等腰三角形等特殊的三角形相结合,解题时需要借助作图进行分类讨论,考查学生数形结合的数学思维能力。
2.2.2 动点与平行四边形相结合
2015年第(4)问和2016年第(3)问中均给出的是平行四边形,相比较而言,2015年第(4)问较为复杂,因为它没有给出平行四边形的顶点顺序。而2016年第(3)问则详细的给出了平行四边形的顶点的顺序,那么在这种情况下,则只需要将动点所表示的边用变量表示出来,然后根据平行四边形的性质即可求解。那么在没有明确给出四个顶点的位置的时候,就需要进行分类讨论,这里就强调了分类讨论的思想。具体解体情况如下:
以2015年第(4)问为例,要求出能使M,N,C,E为顶点的四边形的M和N,由于N在抛物线上,则可设出N的坐标为(-2,n),可设N点坐标,由于M点在抛物线上,故设点M的坐标为(m,y)。然后根据M,N,C,E为平行四边形的可能性,利用对角线将其分为三种情况:(1)EN为对角线,(2)EM为对角线,(3)EC为对角线。根据平行四边形对角线平分可求得对角线的交点横坐标,从而可求得M点的横坐标,再代入抛物线解析式可求得M点的坐标。
此题难度系数较高,主要突破口是如何表示这个平行四边形四个点的组合方式,根据点N和点M所处的位置,利用对角线的不同来进行分类。考察了平行四边形的性质以及分类思想。
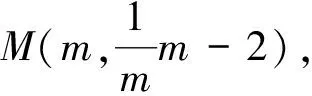
评析:二次函数与四边形结合,该题型主要是将四边形与抛物线结合,四边形顶点或者中点是抛物线上的一动点,既考查特殊四边形的判定定理,也考查抛物线的特征性质。如果给出的是菱形、正方形、圆等其他几何图形,一定要注意每一类几何图形的特点和性质,根据这些性质和题目已知的条件进行分析,做到层层递进,在这个过程中要注意逆向思维以及数形结合的思想方法,做到有理有据,条理清晰,从而达到解题的目标。
2.3 动点与分类讨论相结合
例题4:在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动。过P作PQ⊥OA于Q。设P点运动的时间为t秒(0 (1)求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标; (2)用含t的代数式表示P、Q两点的坐标; (3)将ΔOPQ绕P点逆时针旋转90°,是否存在t,使得ΔOPQ的顶点O或Q落在抛物线上?若存在,直接写出的值;若不存在,请说明理由; (4)求S与t的函数解析式。 此例题中的第(3)问和第(4)问,均涉及到了动点与分类相结合的问题。分类讨论都是由于动点的运动所引起的,在第(3)问中由于有两个动点都可以满足题设条件,故需要分两类情况讨论,而在第(4)问中则是因为动点运动引起变量范围的变化使得我们解题时需要分类讨论。在运动中会出现满足条件的一个临界值,找到这个值就可以确定分类讨论的突破口,从而复杂问题简单化。针对此类问题,要分析题目所给的条件以及题目所要求的目标之间的联系,在这两者之间搭起桥梁就使得我们解题更加方便,学生要重点掌握分类讨论问题,分类问题不仅单独的出现,而且也会出现在动点与几何图形中相结合的问题中,实质上都是由于动点变化引起变量的变化造成的,具体解题如下: 以第(3)问为例:首先要分类讨论,即O点或者Q点在抛物线上,接下来就是分析旋转后这两点的坐标能否用含t的式子表示出来,有了求解(2)的经验,就容易分析,当ΔPOQ绕点P逆时针旋转90°后,点O的坐标为(2t,-2t),点Q的坐标为(3t,-t),再分两种情况讨论。 情况一:0 评析:此问难度系数较大,涉及到分类思想,主要突破口在于分几类,如何进行分类,这也就需要找到分类的临界值,那么这几类的临界值是怎么找出来的,则需要根据题目所要求的结果和已知条件进行分析,在一定范围内满足所求结果,超过这个范围就会发生变化,这也就是要寻找的临界值的特点。分类之后能否画出相应的草图来分析,数形结合解数学应用题的关键和突破口,根据图像可以更加直观具体的看出变量之间的关系,有利于学生更加清楚、深刻的理解题目,从而更好的解题。做题的时候一定要多思考,多问几个为什么,以及多角度,多层次的去分析不同基础条件之间的关联,学会挖掘潜藏的条件,这才是解题的关键进而使看似复杂的问题简单化[4]。 图1 例题1图示 图2 例题2图示 图3 例题3图示 图4 例题4图示 动点与函数相结合,以函数图形为背景,以动点为元素,构造动态型几何图形。上述题目均为动点问题,以动点为问题的研究对象,把函数、方程、直线、三角形、四边形等众多知识点整合在一起。压轴题考察的不是单一的知识点,而是将所有的知识点综合归纳在一起,但是万变不离其宗,几何图形经过翻折、旋转、平移等以及运动的点是否能满足构成三角形的条件或面积是否成比例等问题,但是要意识到图形中依然存在着不变的因素,这些不变的因素就是解决问题的关键,所以我们要学会在动态问题中找到不变的因素,从而达到将动点问题用定量来分析,这就要求学生具备分析问题的能力以及敏锐的视角,将综合的知识点进行分散分析再综合,对知识点进行提炼和整合,以达到解题的最佳效果[5]。 中考压轴题最终考查的还是各个知识点的基础,而目前中学生应用题的解题基础相对薄弱,初中应用题的教学方法不科学,大部分学校提倡题海战术,希望通过反复做题将短期记忆变成长期记忆,然而这种方法只是满足了考试的需求,并没有达到培养学生数学思维以及用数学方法来思考问题的能力,而且学生缺少实际操作培训和分析问题的能力,只是一味的反复加强做题方法的记忆,会导致学生对这种方法没有一个全面而深刻的理解。因此,提高初中数学应用题的解题能力,就要改变传统的应试教学模式,提高教学的灵活度。 首先,要培养初中生对应用题的学习兴趣,这样可以极大程度的调动学生的自主能动性。 其次,要进行应用题分类教学,让学生在实际生活中感受到数学的存在,并对其进行深刻的理解,帮助学生寻找应用题解题规律,让学生成为学习的主体,真正的做到学生学,老师辅助,而不能进行满堂灌式教学,这样时间久了会极大的打击学生自主学习的动力,学习数学最主要的目的是要提高学生的逻辑思维能力以及分析能力,真正达到数学使人周密的效果。新课改下倡导人人都接受良好的数学教育,人人都能在数学中得到不同的发展。 再者在应用题教学中充分利用辅助工具或者进行实验模拟,让学生能更加深刻直观的感受到数学的乐趣,将枯燥抽象的数学知识生活化,让学生能够感受到数学的生活之美,从而更好的去迎合新课标下学习数学的要求。 最后在应用题教学中要变学数学为用数学,要让学生能够感受到数学在实际生活中的应用,正确理解学习数学的理念,最终达到提高思考问题的思维能力以及解决问题分析问题的能力。 在新课改背景下,数学教学目的更加倾向于学生应用能力与解决实际问题能力的培养,比如在讲解函数运用问题的时候,教师要充分利用多媒体等教具,制作出动态的函数图像,培养学生在运动问题上的感知能力,或者可以利用相关生活实例将其抽象成数学问题,让学生在实际生活中去找例子,并对不同的问题进行分析和思考,分组进行讨论,让思维达到沟通和交流,从而更好的达到获取解决问题的能力。数学不仅在科学,生活,工程等各个领域各个方面都有应用,而且还在逻辑思维方面发挥了极其重大的作用。所以学生学好数学,掌握好数学的学习能力,以及解决和分析问题的能力就成了广大教师工作任务的重中之重。 [1] 骆传枢.对数学课程标准(2011年版)“二次函数”的解读与思考[J].中学生数理化:中考版,2012,(11):4. [2] 潘月燕.中考压轴题(二次函数)解题思路探讨[J].课程教育研究,2014,(34):111. [3] 张小林.在运动中分析在变化中求解——2008年中考数学动点型压轴题归类评析[J].中学数学,2009,(5):14-18. [4] 沈莺莺.确定标准好分类,思辨命题来改编[J].中学数学,2014,(10):38. [5] 樊玲.分析数学中考几种压轴题的解题思想[J].数理化解题研究,2014,(5):3. 责任编辑 王菊平 2016-12-22 doi 10.3969/j.issn.1003-8078.2017.03.20 杨媛媛,女,湖北宜昌人,数学与应用数学201301班学生。 吴卫兵,男,湖北蕲春人,讲师,主要研究方向为数学教育。 黄冈师范学院实验教学示范中心实验教学研究项目(zj201606)。 O182.1 A 1003-8078(2017)03-0084-06
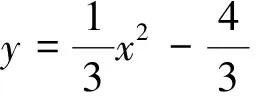




3 二次函数压轴题的解题思路

