一道教材等腰三角形尺规作图题的变式探究

顾建锋，吴志刚

（浙江省嘉兴市南湖区教育研究培训中心；浙江省嘉兴市南湖区大桥镇中学）

一道教材等腰三角形尺规作图题的变式探究

顾建锋，吴志刚

（浙江省嘉兴市南湖区教育研究培训中心；浙江省嘉兴市南湖区大桥镇中学）

变式探究是激发学生学习兴趣、培养学生数学思维品质、渗透数学思想方法的重要途径.文章通过对一道教材尺规作图变式题的作法探究，旨在引导学生多角度、多层次地思考作图思路，在探索问题解决的过程中加深对数学基本事实的理解，巩固所学的知识与技能，渗透重要的思想方法，积累基本的活动经验，进而使学生所学的数学知识能够融会贯通．

尺规作图；变式探究；数学教学

教材是学生学习的蓝本，是中考试题的源泉，是最重要的教学资源.因此，抓住教材中的典型习题，深入思考、适度变式探究，对调动学生的学习积极性、培养学生的思维品质、提高学生的数学素养具有重要的作用，同时教师的专业素养也能得到发展.本文拟就对浙教版《义务教育教科书·数学》八年级上册第58页作业题A组第3题做变式探究，与同行分享.

一、原题呈现

题目如图1，已知∠α和线段a，用直尺和圆规作△ABC，使AB=AC=a，∠B=∠α.

图1

作法：如图2所示.

（1）作∠B=∠α；

（2）以点B为圆心，线段a的长为半径作弧交∠B的一边于点A；

图2

（3）以点A为圆心，线段a的长为半径作弧交∠B的另一边于点C.

△ABC即为所要求作的三角形.

二、变式引申

数学解题教学重在解法指导和思维训练.为此，变式训练必不可少.

变式：如图1，已知∠α和线段a，用直尺和圆规作等腰△ABC，使顶角∠A=∠α，底边BC=a.

分析：变式题在保持原题的结构和结论不变的情况下，将条件进行微调（将原题中的底角∠α和腰长a分别调整成顶角和底边长，其他条件不变），解题要求相比原题有了较大的提高，涉及的知识面变宽，思维深度陡增.

三、作法探究

变式题中，由于所要求作的等腰三角形的顶角和底边确定，故根据全等三角形的判定知识可知这样的等腰三角形唯一确定.即能用尺规作图作出符合条件要求的等腰三角形.

1.利用“圆周角的性质”作图

对于条件复杂的尺规作图题，先作出条件相对弱化的图形，再寻找该图形与所要求作图形之间的联系，是解决问题的一种常用方法.此题所要求作的图形既要满足三角形是等腰三角形，又要使得等腰三角形的顶角为∠α、底边为a，条件多，难度大，直接求作不易，这时考虑将所求作图形的条件弱化，先作出一个边长为a且该边所对的角为∠α的三角形（图3中的△BCD），再思考△BCD的顶点D在怎样的路径上运动能始终保持∠D=∠α，由此想到“同弧所对的圆周角相等”这一性质，于是解决问题的思路柳暗花明.

作法1：如图3所示.

（1）作∠D=∠α；

（2）在∠D的一边上取一点B，以点B为圆心，线段a的长为半径画圆弧，交∠D的另一边于点C；

（3）作△BCD的外接圆；

（4）作线段BC的中垂线交△BCD的外接圆于点A，E；

（5）连接AB，AC.

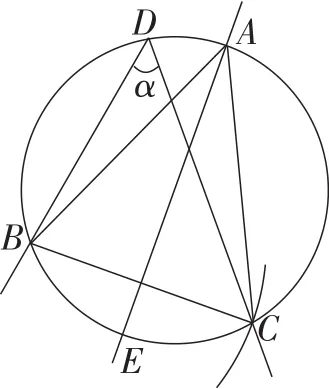
图3

△ABC即为所要求作的等腰三角形.

2.利用“等腰三角形顶角与底角之间的关系”作图

当某一问题直接从条件难以或无法入手时，将条件转化必然成为问题探究的基本途径.此题若能将条件转化到已知底角和底边求作等腰三角形，则问题将迎刃而解.于是想到探究等腰三角形顶角与底角之间的关系，通过计算不难得到：当等腰三角形的顶角为∠α时，它的底角为90°-∠α.于是只要想办法作出一个角等于90°-∠α，则解决问题的思路应运而生.

作法2：如图4所示.

（1）作∠α的平分线；

（2）作线段BC=a，并作出直径为BC的⊙O；

（4）连接BD，CE，并延长交于点A.

则△ABC即为所要求作的等腰三角形.

图4

作法3：如图5所示.

（1）作∠GDH=∠α；

（2）在∠GDH的两边上取点E，F，分别作∠GEF和∠HFE的平分线交于点B；

（3）在射线FB上截取线段BC=a；

（4）过点C作∠BCA=∠CBA交射线EB于点A.

图5

则△ABC即为所要求作的等腰三角形.

3.利用“平行线的性质”作图

要作出满足条件的等腰三角形，若先作出底边BC=a，则顶点A显然在底边BC的中垂线上，这样问题便集中到探究∠DAC=∠α的点A的位置上（如图6）.由于无法直接作出∠DAC=∠α，故而考虑先作出∠DEF=∠α，再利用“两直线平行，同位角相等”的性质进行转化，于是解决问题的思路破茧而出.

作法4：如图6所示.

（1）作∠α的平分线；

（2）作线段BC=a，并作出线段BC的中垂线DE；

（4）过点C作∠BCA=∠DFE，交DE于点A；

（5）连接AB，AC.

△ABC即为所要求作的等腰三角形.

图6

4.利用“相似三角形的相关知识”作图

将难题分解是解决问题的基本策略，依据这一基本策略，将此题分解成两个步骤进行探究的想法油然而生.于是“先作一个顶角为∠α的等腰三角形，再作一个底边长为a的等腰三角形与它相似”或“先作一个顶角为∠α且腰长为a的等腰三角形，然后在此基础上构造与该等腰三角形相似的三角形”的作图思路刀过竹解.

作法5：如图7所示.

（1）作等腰△DEF，使顶角∠D=∠α；

（2）作线段BC=a；

（3）过点B，C分别作∠GBC=∠DEF，∠HCB= ∠DFE，BG，CH交于点A.

则△ABC即为所要求作的等腰三角形.

图7

作法6：如图8所示.

（1）作线段BC=a；

（2）以B为顶点作∠CBD=∠α，并截取BD=a，连接BD，CD；

（3）以点B为顶点作∠CBA= ∠DCB，交CD的延长线于点A.

图8

则△ABC即为所要求作的等腰三角形.

5.利用“邻补角知识”作图

此题的作图难点在于已知等腰三角形的顶角如何作出它的底角，将思维重心聚集于此，就会发现已知角α的邻补角恰好等于所要求作等腰三角形的两底角和，于是问题解决的思路水到渠成.

作法7：如图9所示.

（1）作∠DBE=∠α，并作出它的一个外角∠EBF；（2）作∠EBF的平分线BM；

（3）以点B为圆心，线段a的长为半径画弧交BM于点C；

（4）过点C作∠NCB=∠EBC，交BE于点A.

则△ABC即为所要求作的等腰三角形.

图9

四、思考

用直尺和圆规作出符合一定条件的几何图形，不仅仅是一种需要学生动手实践的操作过程，更是一种需要学生数学思维参与的探究过程，它可以很好地锻炼学生的分析、判断、操作和思维能力.而变式探究则是激发学生学习兴趣、培养学生数学思维品质、渗透数学思想方法的重要途径.因此，在中考复习阶段，对上述教材中的等腰三角形尺规作图题进行变式探究，不仅能激发学生学习数学的兴趣和求知欲，而且还能拓展学生思维的深度和广度，这对学生的学习无疑有着积极的意义.

一道教材尺规作图题经过简单的条件变换，延伸出多种不同的作图方法，且各种作法相互关联，异中有同，能很好地引发学生多角度、多层次、有个性地思考作图思路.同时在具体的作法探究过程中，又需要数学基本活动经验、基本思想、基本技能和分析法的共同参与，协同合作.其中，基本活动经验能让学生联想到曾经习得的基本图形（如作法1中“同弧所对的圆周角相等”基本图形；作法4中“等腰三角形三线合一”基本图形）；基本思想——转化思想能让学生想到将问题转化成“已知底角和底边作等腰三角形”的问题（如作法2～作法7都是将已知顶角转化成底角后作图）；基本技能让学生知道已知顶角如何转化为底角（如作法2、作法3和作法7中通过计算发现了顶角和底角之间的数量关系）；分析法能使学生建立起已知条件与相关知识的联系，让学生明确已具备什么条件，还需要什么条件，是作法探究的起点.这样的作图探究，内涵丰富，思路多元，探究过程中涉及众多的初中数学核心内容，若在中考复习时使用此变式题，引导学生多角度、多层次地探究此题的作图方法，则能让学生在探究问题解决的过程中加深对数学基本事实的理解，同时巩固所学的知识与技能，重温重要的数学思想方法，积累基本的数学活动经验，进而使学生所学的数学知识能够融会贯通，达到“以点带面、以一抵十”的复习效果，这也是此题探究的意义和价值所在.

［1］戴向阳.一道课后习题的“动感”探究［J］.中学数学教学参考（中旬），2013（3）：41-43.

2017—03—10

顾建锋（1975—），男，中学高级教师，主要从事中学数学教学与命题研究.