论“零除零等于零”的数学命题是正确的

倪维多

【摘要】“0÷0=0”的算式符合数学逻辑，是对的.反之，“0除以任何不是零的数都得0”的命题是错的.设想“0不可做除数”的命题是荒诞的.

一、“0÷0=0”的算式符合数学逻辑

1.“0÷0=0”的算式符合数学逻辑.现在就简单论证如下：

① 由四则运算的“零乘任何数都是零”的定律，可知：

“0×0=0”的式子成立，是对的.

因为零于事实上就列在自然数之中.任何数自应包括零.

“零乘任何数都是零”“零乘零等于零”，二者屬全称肯定判断与特称肯定判断的同真关系，乃普通逻辑学或称形式逻辑学之常识，也毋庸置疑.

② 因为，四则运算中乘的逆运算是除，即用乘的相反的运算方法除，从已知得数求出原式中所故有的相应之数.

那么“0×0=0”算式的逆运算式子，必然且只能是“0÷0=0”.

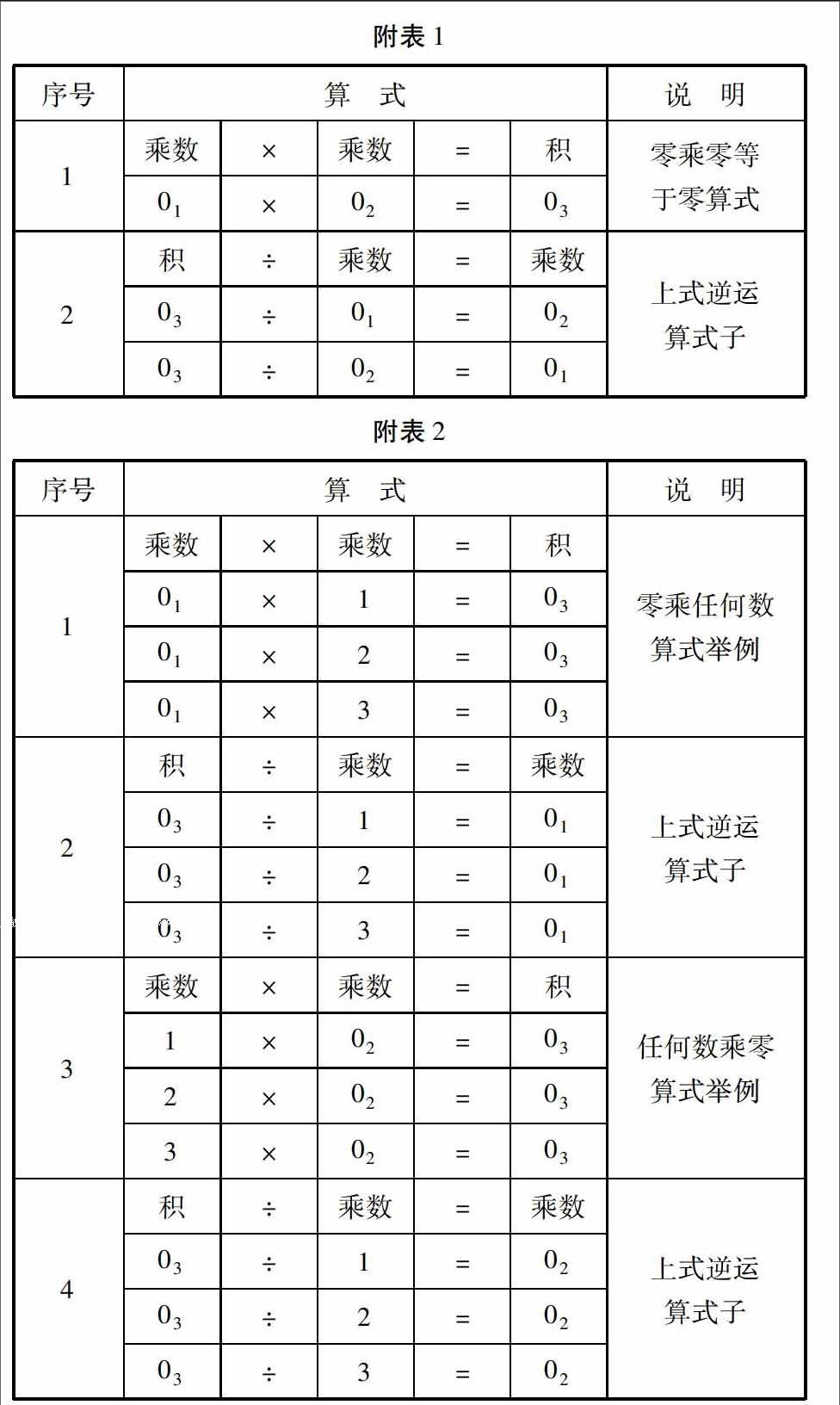
在这里，“0÷0=0”的式子成立.是对的.而“0除以任何不是零的数都得0”的命题是错的.见附表1.

2.由现实社会诸如球类比赛中的0∶0转化而来的0〖〗0记数形式，正与“0÷0=0”的算式之义相通，故也可将此例的数值比关系写成除法的完整等式.即0∶0=0÷0=0.

但是，在同一的社会场所，诸如1∶0，2∶0，3∶0，4∶0，5∶0，或者0∶1，0∶2，0∶3，0∶4，0∶5之类的记数形式，却不能转化为除法的等式去运算.

这又恰好证明，“零除零得零”的命题是对的.而“零除以任何不是零的数都得零”的命题是错的.

二、设想“0不可做除数”的命题是荒诞的

3.在“0÷0=0”的算式之外，设想“0不可做除数”的命题是荒诞的，在数学逻辑领域没有任何意义.

① 首先，在零乘任何数都是零的算式中，处于积位置的只能是0，0之外的自然数，如1，2，3，4，5等，皆非处于积的位置，也就不存在被0除的问题.故曰“0除不是零的数”之概念，于零乘任何数都是零的逆运算中是不会出现的.见附表2.

② 其次，在现实生活及人们关于数学运算题的设置中，于“0÷0=0”的算式之外，由0做除数去除0之外的自然数而求商的问题，也无从发生.

说明：两表中01，02，03的标示法，仅在指明特定的零于“零乘任何数及其逆运算式子”中的固有位置而已.

从以上的简单论证可知，“0÷0=0”算式的真实性和正确性来自两个方面，一是四则运算中“0×0=0”的逆运算式子，二是由现实社会数值比关系转化成了除法的完整等式.在“零乘任何数都是零”的逆运算式子中，因为零之外的自然数只能是乘数，故不可做被除数.在这里，无论用乘数位置的零或积位的零除其余的自然数，都是不合理的.

据此推论出“0不可做除数”命题的荒诞性，还在于它推翻了“0÷0=0”算式的真实性和正确性.

近年来，网络上流传着“零除零可以等于任何数”“零除零的等式不能成立”“零不能做除数”等言论，乃至在学校的讲坛上也堂而皇之地广为传布，故写此文以正之.