巧用多样化算法，构建减法算理

陆佩琴

一、缘起

一名学生的想法：

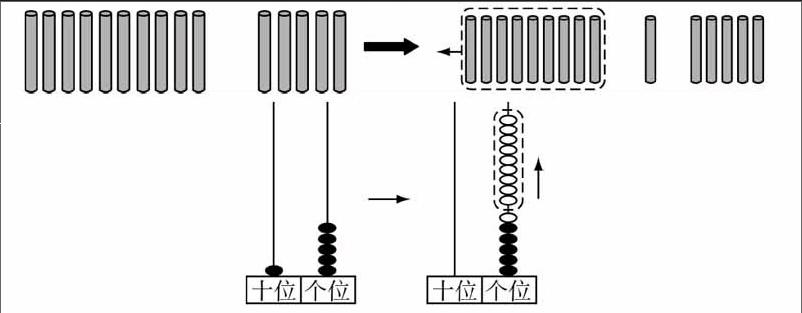
在去年我教学一年级下册“买铅笔（十几减9）”一课之后，一名学生紧跟着我跑出教室问道：老师，我觉得用计数器拨出的15-9=6和用小棒摆出的10-9=1再用1+5=6的方法是一样的（如下图），您觉得是吗？

学生有这样的想法，是不是我的教学中缺少了什么呢？我不禁反思自己的教学：我都是按照教材设计的问题串从小棒操作——计数器操作——脱离模型的计算，一步步进行的，会缺少什么呢？本学期，我尝试从运算能力这一数学核心素养的角度去思考这节课.

二、怎样发展学生的运算能力

计算教学中应该怎样才能更好地发展学生的运算能力？为了弄清楚这个问题，先要弄清楚运算能力的概念.

《课标（2011版）》指出：运算能力主要是指能根据法则和运算律正确地进行运算的能力.培养运算能力有助于学生理解运算的算理，寻找合理简洁的运算途径来解决问题.运算不等同于计算，运算能力也并非一种单纯的、孤立的数学能力.而培养运算能力的核心是让学生理解算理，那15-9=6的算理在哪里呢？在理解算理时要追溯到数的意义，这样来说退位减法的算理就是在不够减时，十位上的一个十可以换成个位上的十个一，然后，经历破十的过程.那怎样才算理解算理了呢？巩子坤、刘萍等人认为，理解算理可以分为四个层次：1.程序理解，2.直观理解，3.抽象理解，4.形式理解.四个层次体现了不同的思维水平，其中形式理解是以前三个层次为基础的，是思维的高水平体现.

回想过去的教学：很多学生在上新课之前，就已经知道了怎么去算15-9，但为什么这样算，却是知之甚少，这就是对减法运算的程序理解；学生能够利用各种形式的小棒操作得出15-9=6，这种利用直观的图像、模型来说明运算的结果就是一种直观理解.（用PPT呈现学生摆出的图示，图略）

用计数器操作拨出15-9=6，也是一种直观理解，但相对于小棒的操作来说，计数器呈现了数的结构，它的操作显得更为抽象，学生理解起来难度要稍大一些.

学生能够用算式15-5=10，10-4=5或语言描述来解释运算的结果，这是一种抽象的理解；少数学生能够用“我知道15-10=5，9比10小1，因此，15-9的结果应该比5大1，就是6”来推理出15-9=6，这种运用已知的规律、定律、定义、并通过逻辑推理来说明运算结果的合理性就是一种形式理解.

怎样在15-9=6的教学中，促进学生对算理的理解由低层次的水平向高层次跃进，同时，促进思维水平的提升呢？联想到“缘起”中学生的想法，我尝试在“计数器拨出15-9”这一环节之后设计一个沟通联系的环节.具体如下：

教学片段：

师：同学们，你觉得用计数器画15-9=6和前面小棒摆15-9=6之间有联系吗？

生：有联系.

师：和哪种摆法有联系？

生1：在计数器上个位先去掉5颗珠子，然后，把十位的1颗珠子换成个位的10颗珠子再去掉4颗和小棒的第（2）种方法实际上是一样的.

师：你是怎么看出来的？

生1：去掉计数器上个位的5颗珠子，就和拿走右边5根小棒一样；把计数器十位上的一颗珠子换成个位的10颗珠子，再去掉4颗，就和从左边10根小棒再拿走4根小棒一样.所以，我觉得它们是一样的方法.

师：你计数器上是拿1颗珠子来换的呀，小棒哪里来的1啊？

生1学生没有回答，同桌补充道：小棒里有1啊，10根小棒不就是1捆吗？

师：哦，计数器上从十位退1当十，相当于小棒操作中把1捆拆成10根.

生2：我觉得先将计数器十位的1颗珠子换成个位的10颗珠子，去掉9颗，剩下1颗和个位的5颗合起来与小棒的第（3）方法是一樣的.

师：你又是怎样看的呢？

生2：计数器上十位的一颗珠子换成个位的10颗珠子，就和小棒的1捆拆成10根一样，从换的10颗珠子里去掉9颗，和从拆开的小棒里拿走9根一样，剩下的1颗和个位的5颗合起来与小棒剩下的1根和5根合起来也是一样的，所以，我觉得这两种方法是一样的.

师：看来小棒操作和计数器操作其实就是15-9=6的两种不同操作形式.你们觉得这两种操作形式最大的相同点在哪里？

生：都要把1个十，换成10个一，才能计算出结果.

把一个十换成十个一，也就是说十位上的1相当于10个，这不正是退位竖式减法算理根基之所在吗？原来算理就蕴含在多样化的算法中.通过学生的观察、对比和交流，学生通过想象、对比，沟通了算法之间的联系，在交流、辨析等思维活动中，学生概括总结出了小棒操作和计数器操作的相同点，为今后理解多位数退位减法的算理奠定了基础.在这种沟通中，学生的抽象概括能力得到了提升，理解水平也上升了层次，运算能力得到发展.

总之，小学低年级的运算教学注重沟通多样化算法之间的联系，在操作、观察、想象、语言交流等思辨活动中，促进对运算算理的理解，在理解中发展学生的抽象思维能力，提升运算能力.