浅谈对数列通项公式求法的认识

辽宁省盖州市第二高级中学 杨 军

高中数学是一个整体结构很强的学科，但是各个模块又显得有独立的特色，数列就是这样的和其他模块有很多纵横联系又有其自身独特知识体系的一个理论板块，数列在理论上和实践中均有较高的价值，是培养学生观察能力、理解能力、逻辑思维能力的绝好载体，高考对数列知识的考察在八十年代末发展到了极致，以后逐渐冷落，但最近几年又逐渐升温，随着与大学知识的接轨，竞赛题的释放，很多省市的高考数学卷都把数列题作为压轴题，而数列通项公式的求法又成为一个热点。本文想总结一下在高中阶段，求数列的通项公式的常用方法和策略。

一、观察法

观察法就是观察数列特征，找出各项共同的构成规律，横向看各项之间的关系结构，纵向看各项与项数n的内在联系，从而归纳出数列的通项公式，然后利用数学归纳法加以证明即可。

例1：在数列{an}，{bn}中a1=2,b1=4且an,bn,an+1成等差数列，bn,an+1,bn+1成等比数列(n∈N*)。求a2,a3,a4及b2,b3,b4，由此猜测{an}，{bn}的通项公式，并证明你的结论。

解：有题设条件得2bn=an+an+1，

a2n+1=bnbn+1

由此得a2=6,a3=12,a4=20,b2=9,b3=16,b4=25

猜测an=n(n+1),bn=(n+1)2

用数学归纳法证明：

(1)当n=1时，有以上知结论成立；

所以当n=k+1时，结论也成立，

由(1)(2)，可知an=n(n+1),bn=(n+1)2对一切正整数都成立。

点评：采用数学归纳法证明多是理科教学内容，较为容易，好掌握。

二、定义法

直接利用等差数列或等比数列的定义求通项的方法叫定义法，这种方法适应于已知数列类型的题目。

例2：等差数列{an}是递增数列，前n项和为Sn，且a1，a3，a9成等比数列，求数列{an}的通项公式。

解：设数列{an}公差为d(d＞0)

∵a1，a3，a9成等比数列，

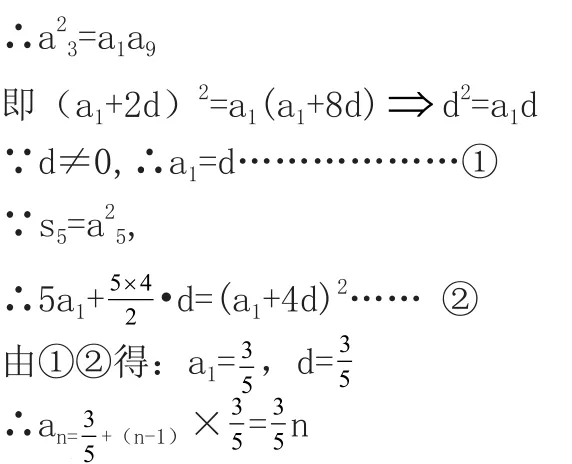
点评：利用定义法求数列通项时要注意不用错定义，设法求出首项与公差（公比）后再写出通项。

三、公式法

若已知数列的前n项和Sn与an的关系，求数列{an}的通项an可用公式

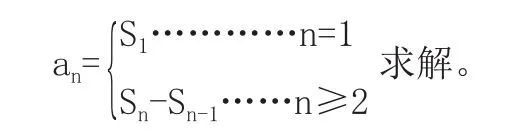
例3：已知数列{an}的前n项和Sn满足Sn=2an+(-1)n.（n≥1）.求数列{an}的通项公式。

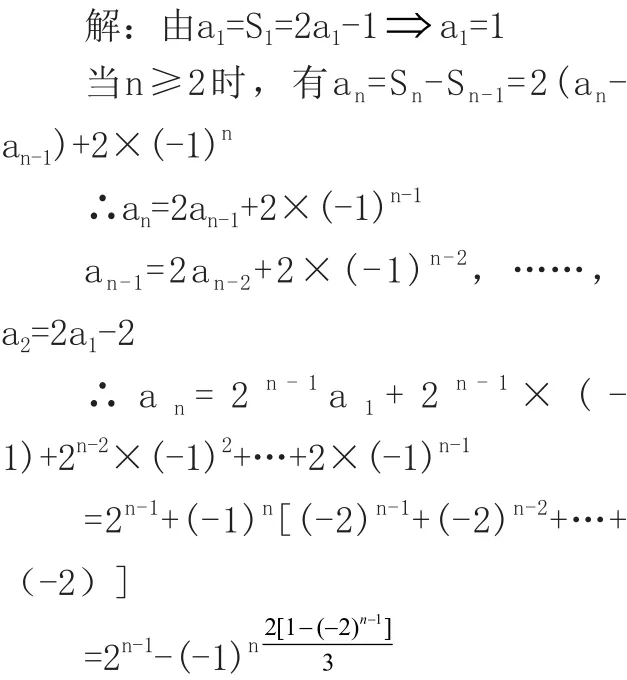
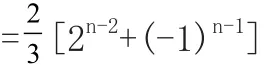
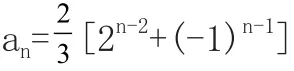
四、由递推公式求数列通项法

对于递推公式确定的数列的求解，通常可以通过递推公式的变换，转化为等差数列或等比数列问题，有时也用到一些特殊的转化方法与特殊数列。

递推公式为an+1=an+f(n)，其中f(1)+f(2)+…+f(n)的和比较易求，通常解法是把原递推公式转化为an+1-an=f(n)，利用累加法(逐差相加法)求解。

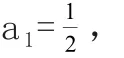
解：由已知得，

令n=1，2,…,(n-1),代入(n-1)个等式累和，即

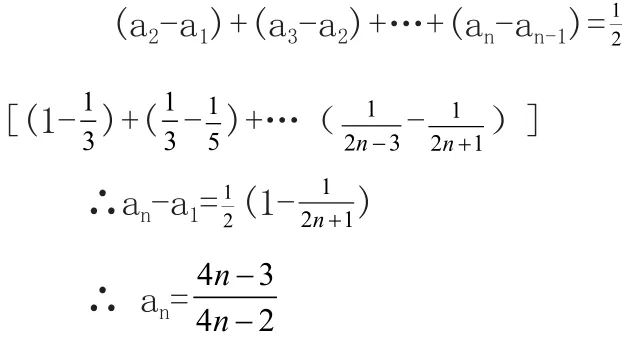
总之，求数列通项公式的方法并不满足以上所述，对于同一问题的求解也不仅是一种方法，只有在平时学习与探究过程中不断地体会与总结，将知识与方法学活，才可以做到游刃有余。