双星问题小议
黑龙江省柴河林业局第一中学 温慧妍
两颗质量可以相比的星体相互围绕着旋转的现象,叫双星。双星问题是万有引力定律在天文学上应用的重要内容之一,亦是高中物理的难点问题之一,由于高中研究的天体运动基本都是一个天体围绕另一个天体做匀速圆周运动的情况,而双星则是两个天体依靠彼此之间的万有引力围绕一个共同的圆心各自做匀速圆周运动,与其它天体问题属于不同模型,两者分析、解决问题的思路不一样,而很多学生已习惯于前者的思维模式,局限于前者的思维定势很难跳出来,故而不能正确地处理双星问题。下面我针对这种情况对双星问题进行详细论述。
一、要明确双星中的两个关系
1.双星中两颗子星做匀速圆周运动的向心力相等
双星中两颗子星相互绕着旋转可看作匀速圆周运动,其向心力由两恒星间的万有引力提供。由于力的作用是相互的,所以两子星做圆周运动的向心力大小是相等的。
2.双星中两颗子星做匀速圆周运动的运动参量T、ω、v的关系
两子星绕着连线上的一点做圆周运动,所以它们的运动周期T是相等的,角速度ω也是相等的,所以线速度与两子星的轨道半径成正比。
【例1】两颗靠得很近的天体称为双星,它们都绕两者连线上某点做匀速圆周运动,因而不至于由于万有引力而吸引到一起,以下说法中正确的是:
A、它们做圆周运动的角速度之比与其质量成反比。
B、它们做圆周运动的线速度之比与其质量成反比。
C、它们做圆周运动的半径与其质量成正比。
D、它们做圆周运动的半径与其质量成反比。
解析:两子星绕连线上的某点做圆周运动的周期相等,角速度也相等。由v=ωr得线速度与两子星圆周运动的半径是成正比的。因为两子星圆周运动的向心力由两子星间的万有引力提供,向心力大小相等,由可知:所以它们的轨道半径与它们的质量是成反比的。而线速度又与轨道半径成正比,所以线速度与它们的质量也是成反比的。正确答案为:BD。
二、要明确双星问题中的两种解法
设双星的两子星的质量分别为M1和M2,相距L ,M1和M2的线速度分别为v1和v2,角速度为ω,由万有引力定律和牛顿第二定律得:


分析思路:
2.①②两式相加(先约掉M1、M2),再与L=r1+r2联立可求得两天体的总质量M、角速度ω、周期T、总质量M与ω2的比值,两天体的总质量M与T2的乘积MT2等。具体如下:

故而可得两天体的总质量M、角速度ω、周期T、总质量M与ω2的比值等。
这样,学生头脑中只需记住这两个关系式,根据题目的实际情况代入求解。这样,学生记忆起来简单、清晰,便于学生理解、掌握此类模型,从而轻松处理相应问题。
【例2】(2008·宁夏)天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为L,试推算这个双星系统的总质量.(引力常量为G)
解:设两颗恒星的质量分别为M1、M2,做圆周运动的半径分别为r1、r2,角速度为ω, 根据题意有


【例3】(2010·全国Ⅰ卷)如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2.已知地球和月球的质量分别为5.98×1024 kg和7.35×1022 kg.求T2与T1两者平方之比.(结果保留3位小数)

解:(1)设两个星球A和B做匀速圆周运动的轨道半径分别为r1、r2,运行周期为T.则有
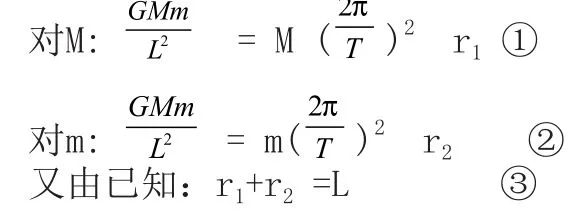
①②两式相加(先约掉M1、M2)与③联立解得

(2)在地月系统中,由于地月系统旋转所围绕的中心O不在地心,月球做圆周运动的周期可由④式得出

式中,M’ 和m’ 分别是地球与月球的质量,L′是地心与月心之间的距离.若认为月球在地球的引力作用下绕地心做匀速圆周运动,月球绕地心运动的周期为T2则


