基于Fiedler矢量的分布式自适应分簇算法

黄庆东，闫乔乔，孙 晴

(西安邮电大学 通信与信息工程学院，西安 710121)

基于Fiedler矢量的分布式自适应分簇算法

黄庆东，闫乔乔，孙 晴

(西安邮电大学 通信与信息工程学院，西安 710121)

针对无线传感器网络分簇(clustering)问题，提出一种基于Fiedler矢量的分布式分簇改进算法。该算法利用Fiedler矢量的元素符号特性对网络进行递归分簇处理，引入网络拓扑信息，根据网络自身的内部连接自适应决定分簇数目,通过Fiedler矢量的元素数值选出簇头，并且算法给簇头子集筛选合适的网关节点以确保簇头子集的连通性。仿真实验表明，在共识频谱感知的基础上，该算法生成的簇头子集与全网络共识所收敛的结果相同，簇头子集共识收敛速度相对更快，耗时短，能够以更好的时效性、更高的能效达到与全网络共识收敛相同的效果。

移动Ad hoc网络；Fiedler矢量；分簇算法；代数连通度

0 引 言

移动Ad hoc网络通过各个节点的相互协作实现信息和服务的共享。但随着网络规模变大，控制开销增大，可扩展性不佳，网络划分成簇以后，簇头和网关节点构成虚拟骨干网，网络可扩充性好，容易实现网络的管理。因此，通过分簇算法将网络划分成簇来提高网络的性能，引起了广大学者的普遍关注[1-2]。

文献[3]提出一种链路分簇方法(link cluster algorithm, LCA)，随机分配节点ID并选择最高ID的节点为簇头，若次高ID的邻居节点有不被最高ID节点所覆盖的节点，次高ID的节点也为簇头。该方法成簇过程简单易行，但会产生过多簇头节点。文献[4]在此基础上适当改进，提出最小ID分簇方法(lowest-ID, LID)，节点随机分配ID，选举相邻各节点中ID值最小的节点作为簇头，距离簇头节点1跳距离的邻居节点作为该簇的成员节点，已成簇的成员节点将不再被选为簇头，避免了簇头冗余。之后，Bednarczyk和Dolowski[5]又提出改进的LID方法，对成簇过程进行了更加严格的限定，但该类算法都倾向于选择ID值偏小的节点成为簇头节点，分簇过程太过理想化。文献[6]提出最高节点度分簇算法(high connectivity degree algorithm, HCDA) ，选取节点度最高的节点成为簇头，减少了分簇数目，并提高了网络的控制性能。但随着节点个数的增多，分簇数目减少，信道的空间复用率降低，网络的整体性能下降。文献[7]在整个网络拓扑的基础上，研究了Fiedler矢量的分布式计算方法，以及应用于Ad hoc 网络中的拓扑推断。文献[8]研究网络图的相关理论以及递归二分谱(recursive spectral bisection, RSB) 分簇算法，该算法限定分簇个数，实用性不佳。

在文献 [7-8]基础上，对分簇算法进行改进，提出基于Fiedler矢量的分布式递归自适应分簇算法，将Fiedler矢量聚类特性和递归二分谱理论相结合，并且引入网络拓扑结构的相关信息改进算法，使网络自适应决定分簇数目。另外，为确保得到的簇头子集是连通的，分簇完成后，进行簇头选择，并通过判断和增加适当的网关节点，保证簇头子集的连通性，从而可以仅在此簇头子集上开展路由功能，以便减少网络信息的冗余传递，提升网络性能，节约带宽和节点能耗，且可以仅由簇头子集中节点维护路由信息表，以提升网络信息传递效率和提升网络的抗毁性。改进分簇算法得到的簇头子集具备连通性，这样不仅可以承载路由功能，同时，可以在此连通子集基础上实施各种分布式应用，进而提升分布式应用算法的综合性能，在提高收敛速度的同时能够降低节点能耗和网络信息传递量，并且能够达到全网络计算时的性能。此算法能够分布式实现，并给出了在簇头子集中进行分布式协作共识频谱感知应用的方法。通过仿真实验证明，在簇头子集中开展分布式共识算法，新算法能够以优于全网络分布式共识算法的收敛速度进行收敛。

1 网络模型及相关概念

1.1 网络模型

假设任意Ad hoc网络节点的连通是对等的，即拓扑结构可以抽象为给定的节点和链路构成的简单无向连通图[7]G=(V,E)，其中，V表示网络的节点集合(包含|V|=K个元素)；E表示网络的节点之间的边集合，即网络中的链路集合。则该图对应的拉普拉斯矩阵L=(lkq)K×K。

(1)

(1)式中：|Nk|表示节点k的度，即节点k的邻居节点数；L=D-A，D=diag(|N1|,…,|NK|)是度矩阵；A=(akq)K×K是网络图对应的邻接矩阵。如果节点k和q相互连接，则akq=1,否则akq=0。拉普拉斯矩阵L是图论中的一个重要矩阵，它是一个对称半正定矩阵。其特征值为

λK≥…≥λ2>λ1=0

(2)

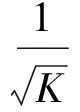
1.2Fiedler矢量的分布式计算

拉普拉斯矩阵隐含了网络的自身编码，网络允许以分布式的方式执行与拉普拉斯矩L的乘法。要计算矩阵矢量乘积Y=LX，假定节点k存储矢量X的第k项元素(用Xk表示)，并且获得了其邻居节点q的存储值，则Y的第k项元素可以表示为

(3)

因此，网内执行幂迭代(power iteration，PI)为

X(i+1)=L·X(i)

(4)

(4)式中，i为迭代指数。设X(0)为随机非零矢量初始化的值，由矩阵理论可知，幂迭代结果收敛到矩阵L的最大特征值λK对应的特征矢量。计算Fiedler矢量需要矩阵L的次小特征值λ2对应的特征矢量XF，故引入矩阵M为

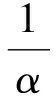
(5)

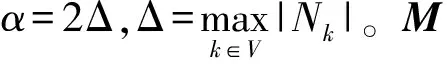
X(i+1)=M·X(i)

(6)

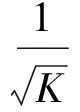
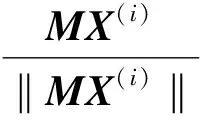
(7)

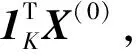
(8)

确保

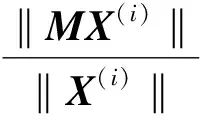
(9)

r(i)的估计可以采用归一化最小均方(normalized least mean square，NLMS)算法，并且

r(i)=μK-1

(10)

因此，(8)-(9)式则为Fiedler矢量及λ2的分布式计算方法。

1.3 比例切

在无向连通图G=(V,E)中，为了对网络进行分簇，需要识别网络中的稠密簇和连接各个簇的边，通过将连接簇的边切割形成簇的划分。假设，簇划分的目标是将网络中的所有节点分成2个非重叠簇集，图论中称为二分图[9]。比例切ρ为二分图中最常用的参数，即

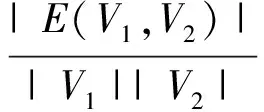
(11)

(11)式中：|V1|,|V2|分别表示节点集合V1,V2的节点数，同时V1∩V2=∅,V1∪V2=V；E(V1,V2)表示图G中连接V1和V2中节点的边集合，即为该图中被切的所有边。图的比例切下界[8]为

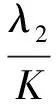
(12)

当图的比例切等于(12)式下界的时，则表示稠密簇的识别和划分已经完成。

2 基于Fiedler矢量的分簇算法

在Fiedler矢量元素符号特性和比例切的基础上，提出改进的递归二分谱节点自适应分簇算法。该算法利用Fiedler矢量元素的正负不同将网络划分为2个子图，然后再计算每个子图的边缘密度，边缘密度值最小的子图即为下一个被划分的对象，再计算其对应的Fiedler矢量，继续划分为2个子图，如此继续递归直到最后被划分的子图比例切等于(12)式下界。改进的RSB节点自适应分簇算法步骤如下。

步骤1 初始化：网络图G记作ω1，即G→ω1；

步骤2 当前网络中的簇个数记作Q，其初始值设为1。∀ωj∈G,j=1,…,Q,表示第j个子集。计算每个簇的Fiedler矢量XF(ωj)，代数连通度λ2(ωj)以及节点个数K(ωj)；

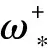
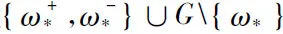
该算法不需要预定义分簇个数，而是根据节点之间的连接关系自适应确定是否能够再继续分簇，如此，使得该算法有更强的实用性和适应性。

3 连通簇头子集的生成

网络中，每个簇由一个簇头和多个成员节点组成，成员节点负责数据的收集，簇头负责各个簇之间的网络通信，通过多跳把组内消息传递到中心节点，达到与外网交换和更新信息[10]的目的。

3．1 簇头子集

Fiedler矢量展现网络各节点的连接关系，其元素值绝对值越小，则该节点连通其他节点的可能性越大[7]。因此，选择每个簇中Fiedler矢量元素绝对值最小的节点作为该簇簇头，则该簇头不仅可以管理簇内所有节点，并且最有可能与其他簇直接通信。该方法虽然不是选择簇头的最优方法，但其有效性却不可忽视。

簇内节点将第一次分布式计算得出的Fiedler矢量元素值提取出来，邻居之间两两相互比较自己的元素值，绝对值较小的节点当选为临时簇头并在簇内广播其当选消息，若在其广播范围内存在其他临时簇头，则元素绝对值较小的临时簇头当选为最终簇头，绝对值相对较大的则变为该簇内的成员节点。

基于以上方法，可以得出分簇结果，如图1所示。图1中，各节点对应的Fiedler矢量元素值如表1所示。虚线将网络节点划分成3个簇，每个簇中Fiedler矢量元素最小的节点1，5和3选举为簇头，组成簇头子集。

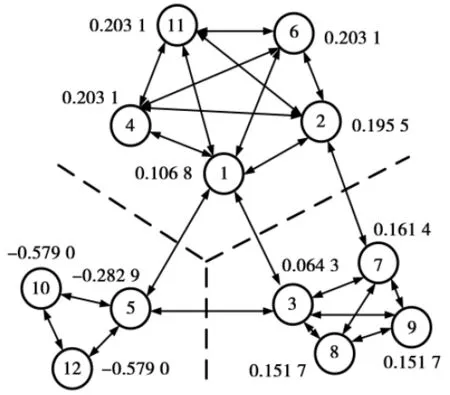
图1 12 个节点分簇效果图
Fig． 1 Cluster rendering of 12 nodes

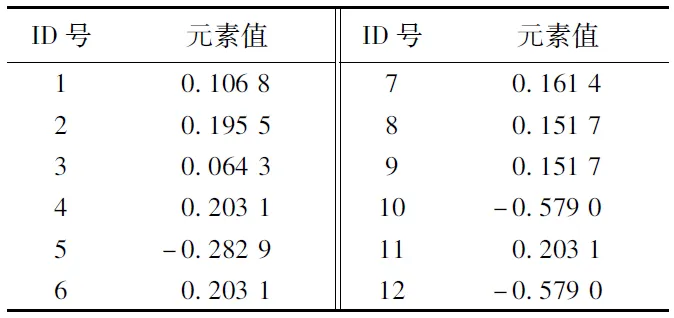
表1 图1 中网络图每个节点对应的Fiedler 矢量元素值
Tab． 1 Entries of the fiedler vector of the network in Fig． 1

3．2 簇头子集连通若节点分布分散，连通情况不佳，可能会出现簇头之间通信隔断的问题，不利于簇头之间的信息传递以及网络的分级结构控制。因此，选择并添加适当的网关节点来确保簇头子集的连通性就相当重要。引入可达矩阵[11]来判断簇头子集的连通性。可达矩阵表示任意2个节点之间是否存在通路。假设Q个簇头组成的无向图，G′=(V′，E′)，{a1，a2，…，aQ}为图G′中的簇头子集，令

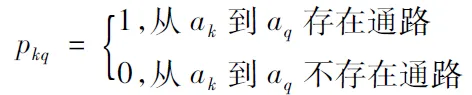
(13)

则矩阵P(G′)=(pkq)Q×Q为无向图G′的可达性矩阵。由无向图G′的邻接矩阵A(G′)，计算出

BQ(G′)=A(G′)+(A(G′))2+…+(A(G′))Q

(14)

(14)式中，A(G′))n是A(G′)的n次幂矩阵。然后，把BQ(G′)中的非零元素换为1，而为零的元素不变，就得出G′的可达性矩阵P(G′)。若可达矩阵中不存在零元素，则表示该簇头子集连通；否则，需要筛选出恰当的网关节点来确保簇头子集的连通性。网关节点选择步骤如下。

步骤1 使用文中的算法步骤，选出Q个簇头，组成簇头子集；

步骤2 用可达矩阵判定簇头子集是否连通。若连通，保存簇头子集节点，结束；若不连通，执行以下步骤；

步骤3 选出所有非簇头子集节点中Fiedler矢量元素绝对值最小的节点作为临时网关节点，加入簇头子集，验证新的簇头子集是否连通，若连通，确定临时网关节点为网关节点，结束；若不连通，重新选择绝对值次小的节点作为临时网关节点，以此类推；

步骤4 若一个网关节点无法使得簇头子集连通，则确定Fiedler矢量元素绝对值最小的节点为第一个网关节点，重复步骤3选择下一个网关节点，直至簇头子集连通。

网关节点的添加确保了簇头子集的连通性，为在缩减的簇头子集上开展各种分布式算法以及路由算法的实现提供了便利。

4 仿真结果及分析

分簇之后，在簇头子集中开展分布式协作共识频谱感知算法[12-13]。协作共识频谱感知分为2个步骤：①次级用户在每一个时隙的开始测量主用户数据；②各个次级用户与邻居用户建立通信链路并交互它们各自检测输出结果信息，直到频谱感知达到共识。在分簇的基础上，普通节点探测并收集信息，簇头子集单步即可与簇内的成员节点相互通信，并在簇头子集上形成快速而稳定的共识，再将共识结果传输给网络中的其他普通节点来提高共识状态的收敛速度，并且最终一致收敛的结果保持稳定。

构建一个随机网络拓扑图，在1×1二维空间随机分布K=24个网络节点，预定义欧氏距离r=0.5。如果任意2个节点之间的距离小于半径r，那么这2个节点之间存在链路，形成网络拓扑结构图。

单次实验结果如图2所示，K=24，r=0.5。图2a为采用文献[13]方法的全网络节点收敛情况；图2b为改进算法簇头子集节点收敛情况，簇头子集节点包含簇头节点和必要的网关节点，共5个节点。由图2可知，分布式结果最终收敛，且簇头子集节点收敛更快，全网络收敛需要迭代15次左右，而簇头子集节点5次左右达到收敛，并且收敛结果一致。

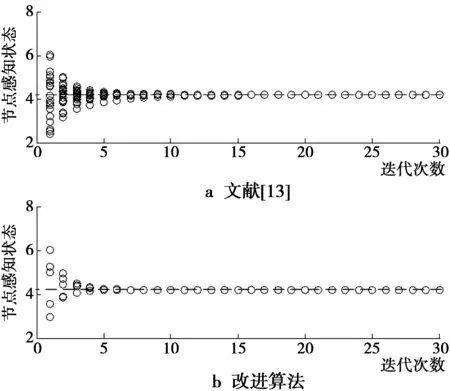
图2 24节点网络(r=0.5)Fig.2 Network of 24 nodes(r=0.5)

网络拓扑图随机生成，具有一定的偶然性，为此，基于蒙特卡罗(Monte Carlo，MC)思想，重复100次上述实验，筛选出单次实验中每次迭代的节点能量最大/小值作为边界考察收敛情况，然后对100次实验取节点感知结果的最大/小平均值来验证该算法的有效性，如图3所示。图3中每次MC实验，参数和方法与图2相同，重复100次。统计结果显示，图3中全网络节点执行分布式协作共识平均需要迭代27次左右收敛；而在簇头子集上执行分布式协作共识平均只需迭代16次左右收敛。由图3可见，全网络节点和改进簇头子集节点最终收敛结果一致，并且，改进簇头子集节点达到共识的收敛速度更快。

另外，对于100次MC实验的簇头进行统计平均，平均簇头数为7.95。由此可知，如果在簇头连通子集中建立路由功能，则仅由约8个节点来维护和管理路由信息表，而不是此Ad hoc网络中的24个节点共同维护路由信息表，而且信息的传递主要由此8个节点完成，进而降低了路由节点维护的开销和网络带宽的占用。同时，在改进算法所得的簇头子集中开展分布式共识算法时相比较文献[13]，信息可以更快速地整合，收敛速度会更快，而且可以减少冗余数据传输、节约带宽同时降低节点能耗。

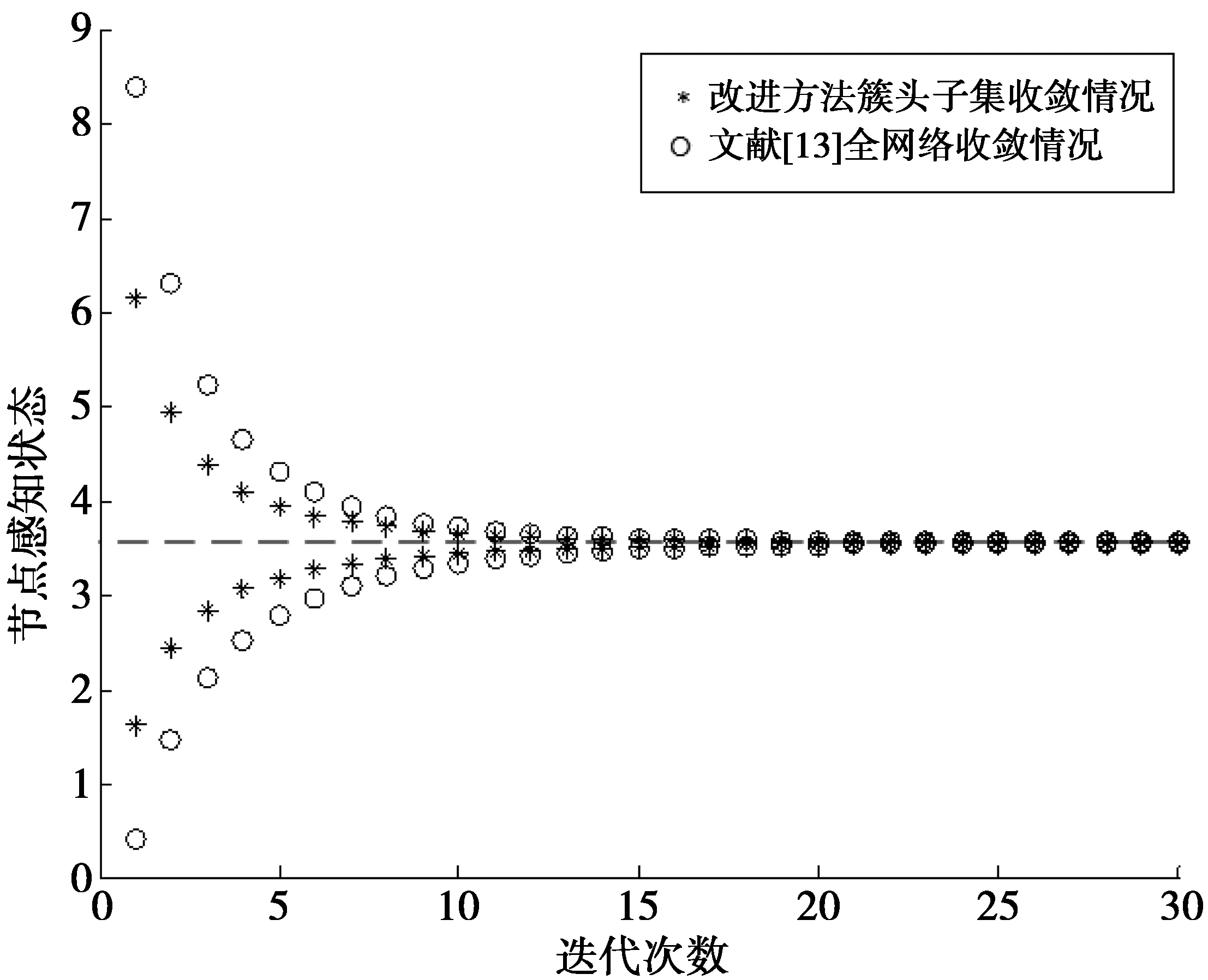
图3 平均收敛图Fig.3 An everage convergence graph

5 结束语

文章提出的基于Fiedler矢量的分布式递归自适应分簇改进算法，将Fiedler矢量聚类特性和递归二分谱算法相结合，并引入网络拓扑结构的相关信息改进算法，使网络自适应决定分簇数目，再选出簇头，为确保簇头子集的连通性，必要时需要增加适当的网关节点。改进算法可以完全分布式实现，并在此连通簇头子集上开展分布式共识算法进行分布式应用拓展实验。实验结果表明，改进方法相比原算法，提高了网络节点的收敛速度，利用簇头子集节点收敛结果能够更快地获得稳定共识。

改进算法完全分布式实现，并自适应确定网络分簇个数，为确保簇头子集的连通性根据需要适当选择和添加网关节点，以便于将来在簇头子集中实现路由功能，进行路由信息表维护，提高路由效率，同时降低路由维护成本，节约通信带宽，减少信息冗余。改进算法所得簇头子集能够进行信息的快速汇集。仿真实验验证了簇头子集在分布式共识应用中的优良性能。

[1] JS W, RH S. Cluster Monte Carlo algorithms [J].Physics A-Statistical Mechanics and Its Application, 2015, 167(3):565-579.

[2] TZORTZIS G, LIKAS A,TZORTZIS G. The min-max k-Means clustering algorithm[J].Pattern Recognition, 2014, 47(7):2505-2516.

[3] BEIN D, DATTA AK, JAGGANAGARI CR, et al. A self-stabilizing link-cluster algorithm in mobile ad hoc networks[C]//Proceedings of the 8th International Symposium on Parallel Architectures, Algorithms and Networks. Las Vegas: Springer, 2005: 436-441.

[4] NGUYEN VD, KIM OTT, DANG DN ，et al. Application of the lowest-ID algorithm in cluster-based TDMA system for VANETs [J]. International Conference on Information Networking, 2015,15(3):25-30.

[5] VASUDEVA A, SOOD M. Sybil Attack on lowest ID clustering algorithm in the mobile ad hoc network[J]. International Journal of Network Security & Its Applications, 2012, 4(5):135-147.

[6] HUANG C, NING Y. Study on cluster-based dynamic routing algorithm in power line communication network[J]. IEEE International Conference on Automation & Logistics, 2012, 17(4):461-465.

[7] BERTRAND A, MOONEN M. Distributed computation of the Fiedler vector with application to topology inference in ad hoc networks [J]. Signal Processing, 2013, 93(5):1106-1117.

[8] BERTRAND A, MOONEN M. Seeing the bigger picture: How nodes can learn their place within a complex ad hoc network topology [J]. IEEE, Signal Processing Magazine, 2013, 30(3):71-82.

[9] CHAN T F, CIARLET T C, SZETO W K. On the optimality of the median cut spectral bisection graph partitioning method [J]. SIAM Journal on Scientific Computing, 1997(18):943-948.

[10] WU C M, CHOU S C, LIAW H T. A trend based investment decision approach using clustering and heuristic algorithm[J].Science China Information Sciences, 2014,57(9):1-14.

[11] 王欣欣,李金宝.关于由邻接矩阵求可达性矩阵的方法[J].吉林化工大学学报，2005, 22(4)：89-93. WANG Xinxin, LI Jinbao. A method for computing reachability matrix of adjacency matrix[J].Journal of jilin institute of chemical technology, 2005, 22(4):89-93.

[12] NEWMAN M. Networks. An introduction[M]. New York, NY, USA: Oxford University Press, 2010.

[13] LI Z, YU F R. A distributed consensus-based cooperative spectrum-sensing scheme in cognitive radios [J]. Hicular Technology IEEE Transactions on,2010,59(1)：383-393.

(编辑：刘 勇)

s：The National Natural Science Foundation of China (61301091,61271276); The Project Funding Issue of Shaanxi Provincial Department of Education of China(11JK0929)

Distributed adaptive clustering algorithm based on Fiedler vector

HUANG Qingdong，YAN Qiaoqiao，SUN Qing
(School of Communication and Information Engineering Xi’an University of Posts and Telecommunications, Xi’an 710121, P.R. China)

To solve the problems of node clustering in the wireless sensor network, an improved distributed adaptive clustering algorithm based on Fiedler vector is proposed. The algorithm utilizes the positive and negative characteristics of the Fiedler vector element to cluster recursively, and leads into the network topology information, then determining the number of clustering adaptively in line with its own internal network connections. The algorithm filters out the cluster head through the Fiedler vector element values. In addition, it adds appropriate gateway nodes for head nodes to ensure that the cluster heads set is connected. Simulation results show that on the basis of the consensus cooperative spectrum sensing, there’s little difference between the result of the cluster heads set consensus and that of the whole network consensus, but the cluster heads set consensus converges faster and gets a shorter time-consuming. It can achieve the same performance as the the whole network algorithm with better real-time performance and higher energy consumption.

mobile Ad hoc network; Fiedler vector; clustering algorithm; algebraic connectivity

2016-06-23

2017-04-20 通讯作者：闫乔乔 xueqiao1017@163.com

国家自然科学基金(61301091，61271276)；陕西省教育厅项目(11JK0929)

10.3979/j.issn.1673-825X.2017.03.003

TN911.23

A

1673-825X(2017)03-0301-06

黄庆东 (1976-)，男，新疆沙湾县人，副教授，硕士研究生导师，主要从事分布式信号处理，阵列信号处理、低复杂度算法等方面研究。E-mail: huangqingdong@xupt.edu.cn。

闫乔乔(1991-)，女，陕西西安人，硕士研究生，主要研究方向为通信信号处理及应用。E-mail: xueqiao1017@163.com。

孙 晴(1988-)，女，河南永城人，硕士研究生，主要研究方向为通信信号处理及应用。E-mail: sunqing_hn@163.com。