一种宽间隔混沌跳频序列快速生成方法

许 尧，戴伏生，王 钢

(1.哈尔滨工业大学 电子与信息工程学院，哈尔滨 150001;2.哈尔滨工业大学(威海) 信息与电气工程学院，山东 威海 264209)

一种宽间隔混沌跳频序列快速生成方法

许 尧1，戴伏生2，王 钢1

(1.哈尔滨工业大学 电子与信息工程学院，哈尔滨 150001;2.哈尔滨工业大学(威海) 信息与电气工程学院，山东 威海 264209)

针对比特抽取法在产生混沌跳频序列时实时性不佳的问题，提出一种基于分段迭代的混沌跳频序列生成算法。将分段迭代产生的混沌映射轨道实值点表示成二进制小数，采用周期多比特重叠抽取和非线性矩阵变换相结合的方法以及改进的随机平移替代法生成宽间隔序列。仿真结果表明，在平衡性、汉明相关性、跳频间隔及抗预测能力等跳频序列性能不低于现有算法的前提下，其平均迭代次数可减少约45%，且在实时性、存储空间占用量和扩展序列周期方面具备优势。经验证，该算法适用于要求灵活更换跳频图谱的无线跳频通信系统。

无线通信；跳频序列；混沌理论；宽间隔图谱；长周期码

0 引 言

跳频保密通信对于抵抗恶意侦测干扰及截获等方面具有明显优势。但随着计算机运算速度的提高，混沌预测算法的改进[1]，信号处理新理论和新技术的发展[2]以及云计算技术的出现[3]，跳频规律被破译的可能性增加，便携式跳频保密无线通信设备的优势也受到了极大挑战。针对这些情况，迫切需要研究出既能嵌入到便携式无线通信设备，又能随时随地生成跳频序列和更换无线频段的功能部件，以满足保密无线通信的需要。

跳频序列设计是保密无线通信功能部件的一项关键技术。性能优秀的跳频序列应该具备平衡性好、正交性和随机性强以及跳频序列码数量多等特点。基于混沌理论的跳频序列生成系统是一个动态非线性跳频序列生成系统，因其具有良好的初值敏感性、遍历性和安全保密性而受到青睐。虽然，多年来在构造混沌跳频序列方面取得了较大进展，在理论上提出了很多有效方法，但是这些方法需结合当前技术情况和实际应用有待进一步改进。如经典的混沌轨道多值量化法[4-5]，利用混沌映射和余弦映射产生的跳频序列具有较好的性能，但其互相关峰值较大不利于无线电台多址组网。改进的多值量化法[6]虽能较好地解决互相关峰值较大的问题，但却是以增加迭代次数为代价。结合伪随机数生成技术的中间多比特量化方法[7]，虽然生成的跳频序列各项性能都很良好，且减少了运算量及混沌特性损失，也扩展了序列周期，但其会受限于计算机字长。文献[8]在文献[4-7]的基础之上，将混沌映射产生的实值点表示成二进制小数，然后从中按列抽取多个比特生成跳频序列，较好地解决了混沌特性损失和计算机字长限制等问题，但其在生成长周期跳频序列情况下，不仅实时性不佳，而且占用存储空间较多不利于硬件实现。基于Tent映射双向耦合映象格子法[9]，虽然较文献[8]提高了跳频序列产生的实时性，但其在迭代次数、序列性能和扩展序列周期上却基本没有改进。

为找到在保持生成跳频序列长周期且各项性能都优良的基础上，既能降低存储空间，实时性良好，又能减少迭代次数的跳频序列生成折中算法，本文提出一种结合非线性矩阵变换法，并采用分段迭代的周期多比特重叠抽取方法生成跳频序列。最后，进行了仿真实验对比。

1 混沌跳频序列生成算法

1.1Logistic满映射

Logistc满映射的迭代式[8]可表示为

xn+1=f(xn)=4xn(1-xn),

xn∈(0,1)

(1)

(1)式中：xn为当前时刻迭代值；xn+1为下一时刻迭代值。

其轨道点概率密度ρ(x)为

(2)

随着周期改变初值法[10]和扰动法[11-12]等克服计算机有限精度方法的发展及上述映射自身极强的初值敏感性，理论上可产生无穷多的非周期混沌跳频序列，十分有利于多址组网。

1.2 非线性转移矩阵变换

在长周期跳频序列产生过程中，为增加跳频序列的复杂度，利用非线性转移矩阵Tk×n把kbit原始跳频状态码转换成nbit(k>n)。当矩阵Tk×n的秩R(Tk×n)=maxR(Tk×n)=n时，Tk×n会具有非奇异性。此时用Tk×n进行非线性矩阵变换产生的跳频序列满足均匀性和随机性的要求，而且频率撞击数将会随着压缩比特k/n的增长呈指数增长规律[13]。

1.3 改进的随机平移替代法

(3)

(3)式中：q为频点数；d为要求的最小频隙间隔；p1用d+1代替；p2用q-2d-1代替；ds(Xi,Xi+1)代表Xi和Xi+1之间的狭义跳频间隔，其值为

ds(Xi,Xi+1)=min{|Xi+1-Xi|,q-|Xi+1-Xi|}

(4)

1.4 基于分段迭代的周期多比特重叠抽取跳频序列生成算法

为有效躲避侦测干扰，同一子网内的通信设备可根据约定随时更换跳频图谱，则跳频序列的产生需满足条件：①较好的实时性；②占用较少存储空间；③可灵活快速地产生任意长度的跳频序列。为此，提出一种基于分段迭代的周期多比特重叠抽取跳频序列生成算法，并用非线性矩阵变换提高跳频序列的抗破译能力。算法详细步骤如下。

Step 1(分段迭代) 设要生成周期为N、频点数为q的跳频序列X={X1,X2,…,XN}。定义正整数集合A={1,2,…,q}分别代表频点{f1,f2,…,fq}，则有Xi∈A,i=1,2,…,N。设定计算机精度为m，比特截取起始位置为K，截取长度为L。将跳频序列的产生分为若干段，每段利用 (1) 式产生lbq个混沌实值点x={x1,x2,…,xi,…,xlbq}，并分别写成m比特的二进制数{b1(xi)，b2(xi)，…，bj(xi)，…，bm(xi)}，其中bj(xi)∈{0,1}，便可得一个lbq×L的矩阵

(5)

Step 2(比特重叠抽取) 对矩阵V1按列依次进行周期比特重叠抽取。这样抽取得到的跳频序列是贝努利序列[8]。为表示方便，将V1按列写成行矩阵

V2=[bK+1(x1)…bK+1(xlbq),bK+2(x1)…

bK+2(xlbq),…,bK+L(xlbq)]

(6)

具体抽取方法为：第n次比特抽取起始位置为矩阵V2的第Sn=⎣(lbq+1)/2」×(n-1)+1个比特，符号“⎣」”代表向下取整，每次抽取(lbq+1)个比特并利用转移矩阵T(lbq+1)×lbq进行非线性变换，便可实时产生q元跳频码。每段迭代可产生Q=⎣(lbq(L-1)-1)/⎣(lbq+1)/2」」+1个跳频码。图1给出q=8，K=10，L=3时的比特重叠抽取示意图。

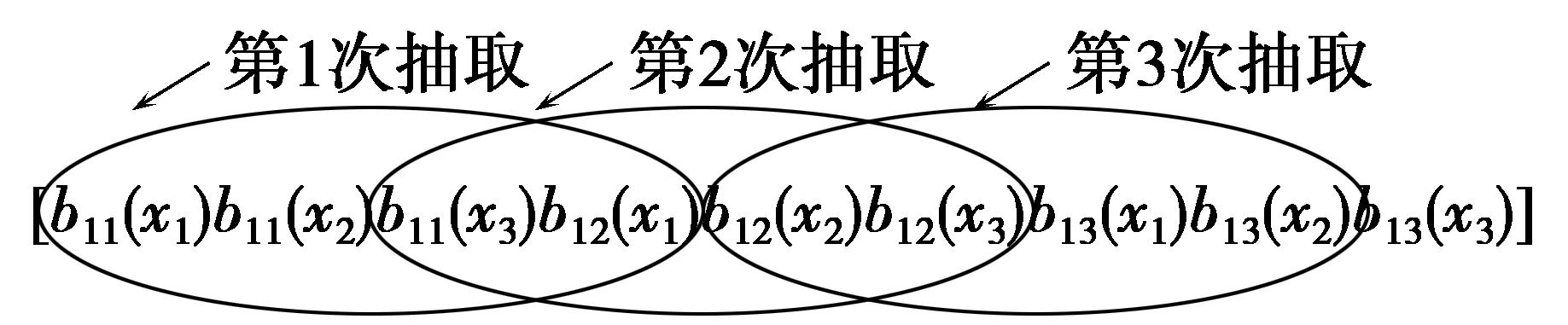
图1 比特重叠抽取示意图(q=8,K=10,L=3)Fig.1 Schematic of reshaping overlapped extraction (q=8,K=10,L=3)

Step 3(循环执行) 每完成一次Step 1和Step 2，便实时释放存储空间。再用前一段迭代中的xlbq+1作为下一段迭代的初值，如此循环执行(N/Q)次Step 1和Step 2，便能生成规定长度的跳频序列。

Step 4(宽间隔处理) 若需宽间隔序列，则每产生一个跳频码便用改进的随机平移替代法对其进行宽间隔处理，不会影响实时性能。

在产生实用的长周期码时，改进方法因分段迭代的原因，其所需存储空间lbq×L远小于文献[8]所需存储空间N×lbq，实时性与文献[9]相当并优于文献[8]。三者所需平均迭代次数由大到小为：文献[9]、文献[8]和改进方法。为直观对比迭代次数大小，定义迭代比为改进方法的迭代次数与文献[8]的迭代次数之比。图2为迭代比与lbq和L(考虑到实际应用，参数取2≤L≤50，2≤lbq≤50)的三维关系图，由图2知迭代比随q和L的增大而趋于0.51。经计算，迭代比取值范围为[0.51, 1]，均值约为0.55，说明改进方法可平均减少约45%的迭代次数。

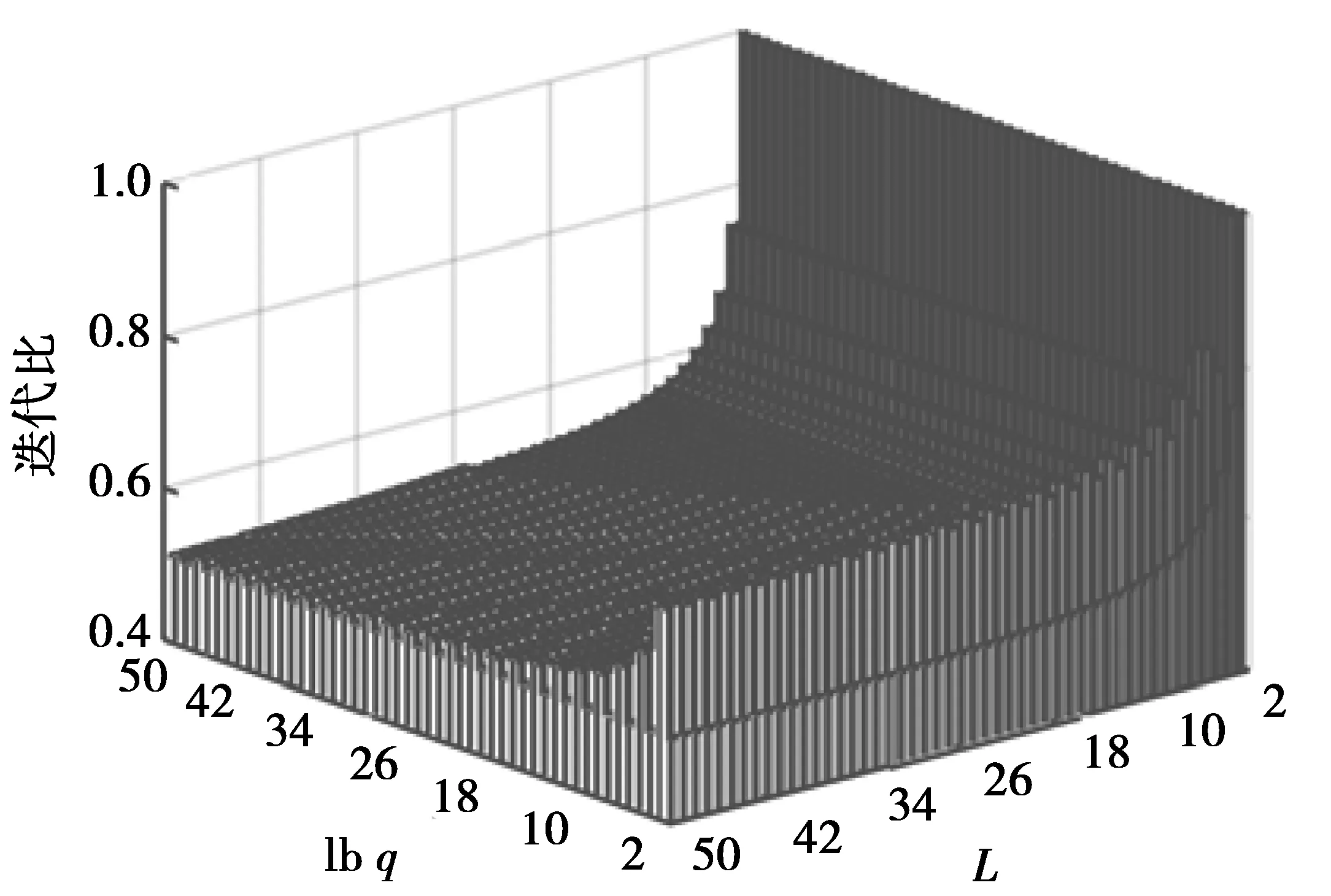
图2 迭代比三维关系图Fig.2 3D relation graph of iteration ratio

2 性能对比

本节研究改进方法产生的非宽间隔序列和宽间隔序列，对比它们的随机性、跳频间隔、均匀性、复杂度、相关性及抗预测能力等与文献[8]和文献[9]产生的序列(文献[9]产生宽间隔序列)的差异。为方便比较，计算机精度m取51，频点数q分别取64,128和256，截取起始位置K取10，截取长度L取lbq，宽间隔距离d取10，采用双精度迭代。

2.1 随机性

抗截获能力强的跳频序列应具有良好的伪随机性，应像高斯白噪声一样拥有平坦的功率谱。因Welch功率谱估计法[15]可减小估计谱的方差和失真，故用此法估计跳频序列的功率谱。

实验中，每个周期长度在取相同初值条件下分别产生4种跳频序列。用Welch法将序列分为3段，每段长N/2，重叠长度为N/4；然后对每段数据分别进行加blackman窗处理，FFT(fast Fourier transform)法求功率谱；最后求3段功率谱的均值，得到其估计谱。限于篇幅，图3只给出q=128时，改进方法产生的宽间隔序列和高斯白噪声的估计谱对比结果，其他情况下的结果与之类似。由图3可知，改进方法产生的宽间隔序列具有类似于白噪声的随机特性。

2.2 跳频间隔

为有效躲避敌方干扰，跳频序列应尽量减少频隙滞留。同时宽频隙间隔也是实现频率分集和抗多径衰落的必要条件。相比满足广义跳频间隔的跳频序列，满足狭义跳频间隔的可以抵抗更多形式的干扰[16]。结合(4)式给出平均狭义跳频间隔davg和最小狭义跳频间隔dmin分别为

(7)

dmin=min{ds(Xi,Xi+1),i=1,2,…,N}

(8)

(7)-(8)式中，(i+1)按模N取值。

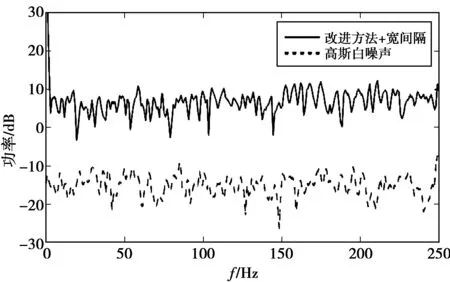
图3 估计谱Fig.3 Estimated spectrum

由按集平均|Xi+1-Xi|的分布可推导得到ds(Xi,Xi+1)的分布如表1所示。

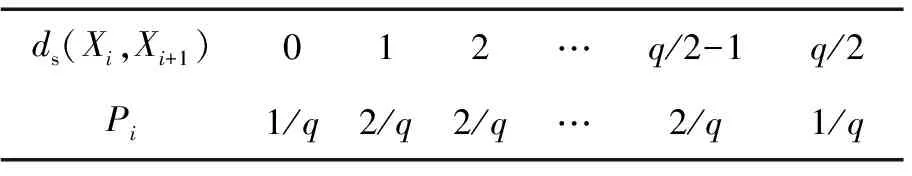
表1 ds(Xi,Xi+1)的概率分布

经计算，可得狭义跳频间隔理论均值为E(davg)=q/4。实验中，每个周期长度随机选取100个初值，分别产生跳频序列并计算其平均狭义跳频间隔统计均值。限于篇幅，表2只给出q=128，N分别取64，128，256，512和1 024时的仿真数据。可看出文献[8]方法和改进方法产生的序列的跳频间隔性能相近，且趋于理论值32。但研究发现，这2种方法会存在频隙滞留问题。例如当N=256，q=128时，两者的最小跳频间隔统计均值分别为0.09和0.16，且在100条跳频序列中分别有87和90条存在频隙滞留。而文献[9]方法和改进方法在相同条件下产生的宽间隔序列则不会存在频隙滞留，其最小跳频间隔统计均值分别为6.50和11.02。结合表2可知，改进方法产生的宽间隔跳频序列的间隔性能要优于其他3种方法。

2.3 均匀性

采用平衡特性参数δ分析跳频序列的均匀性，平衡特性参数公式为

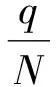
(9)

(9)式中，fi为第i个频率在一个序列周期中出现的次数。δ越接近0，跳频序列的均匀性越好。

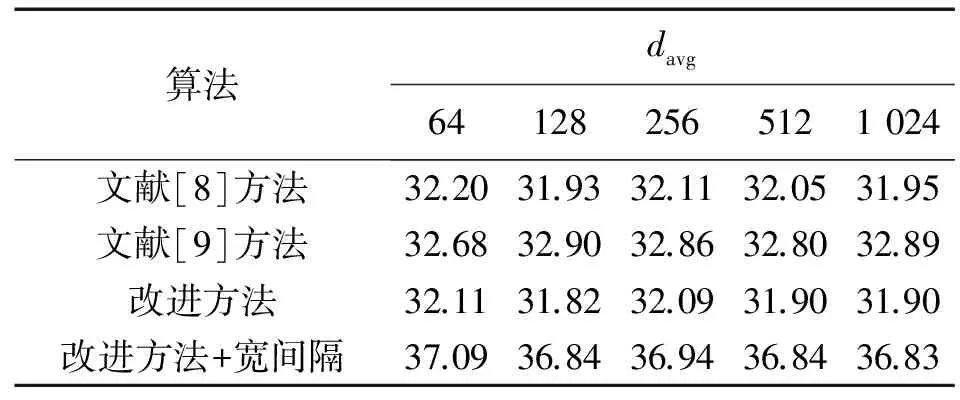
表2 平均狭义跳频间隔统计均值(q=128)

实验中，每个周期长度随机选取100个初值，分别产生跳频序列并计算它们的平衡特性参数统计均值δ。q=64，q=128和q=256时的仿真结果均表明：文献[8]方法、文献[9]方法、改进方法和改进方法且宽间隔处理产生的跳频序列具有几乎一样的均匀性，且随着序列周期的增大，跳频序列的均匀性越来越好。表3仅给出q=128，N分别取64，128，256，512和1 024时的实验结果，其他情况下的结果与之类似。

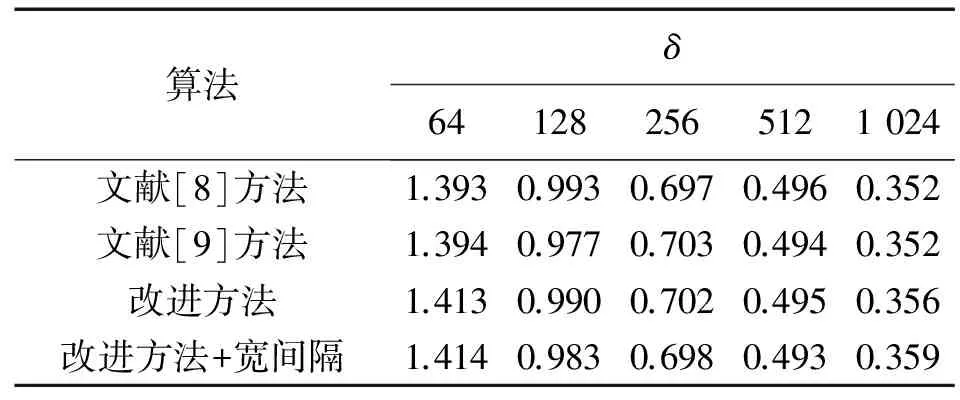
表3 跳频序列的平衡性参数统计均值δ(q=128)

2.4 相关特性

具有良好相关特性的跳频序列有利于跳频通信系统进行多址组网。不同用户同一时刻使用相同的频点则会发生频率碰撞[17]。经常利用汉明相关值来衡量跳频序列的相关性能。由文献[8]可知汉明互相关公式为

0≤τ≤N-1

(10)

(10)式中，(i+τ)按模N取值并有

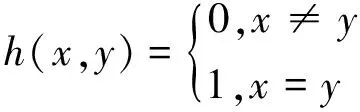
(11)

当X和Y为同一条序列时，(10)式变为汉明自相关公式。下面给出归一化的汉明自相关旁瓣均值、峰值公式和归一化的汉明互相关均值、峰值公式分别为

(12)

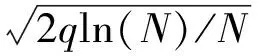
(13)

(14)

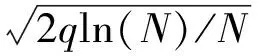
(15)

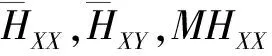
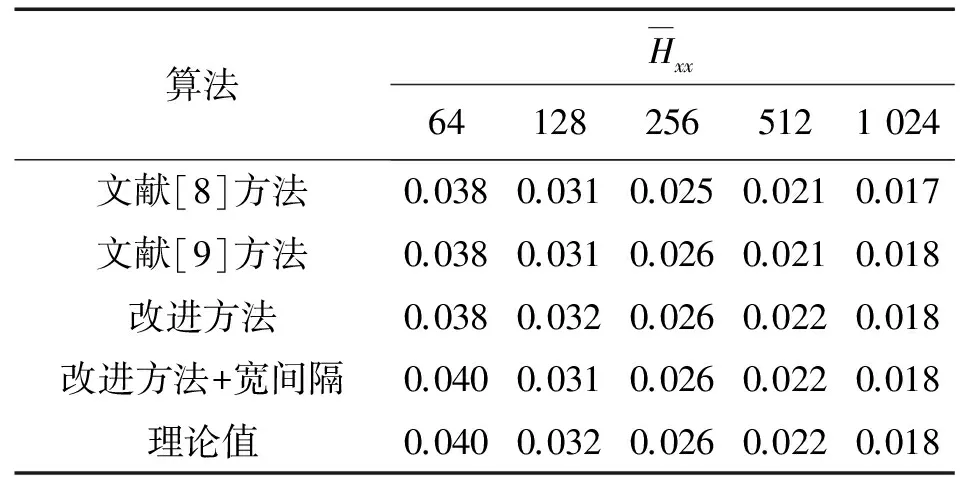
表4 跳频序列的自相关旁瓣峰值统计均值(q=128)

2.5 复杂度

跳频序列的复杂度是衡量跳频通信系统抗截获和抗干扰能力的重要标准[18]。采用文献[19]中的FuzzyEn测度来分析跳频序列的复杂度。FuzzyEn测度值越大，序列的复杂度越高。当N=1 024，q=256，初值为0.161 707 81时，4种跳频序列的FuzzyEn测度值如图4所示。可以看出，相同条件下，跳频序列复杂度由高到低对应的产生方法依次是：改进方法、改进方法且宽间隔处理、文献[8]方法和文献[9]方法。其中，后3者产生的跳频序列的复杂度随精度增大而趋于相同。另外，宽间隔处理会使原有跳频序列的复杂程度有所降低，在实际应用中应综合考虑选择使用。

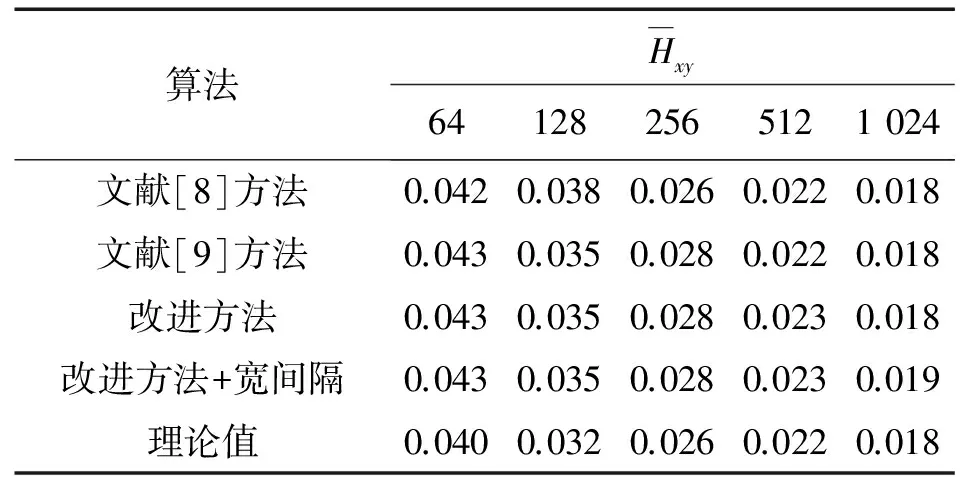
表5 跳频序列的互相关峰值统计均值(q=128)

2.6 抗预测能力

为防止跳频通信系统被预测干扰，跳频序列应该具有较好的抗预测能力。实验中，每个周期长度在取相同初值条件下分别产生4种跳频序列，再采用少参数Volterra自适应混沌预测法[20]分别对它们进行预测。将序列前500个值去除，然后用300个样值训练二阶少参数Volterra滤波器，再预测后100个值，评测标准采用文献[20]中的预测均方误差。预测均方误差越大，说明混沌跳频序列的抗预测能力越强。对文献[8]方法、文献[9]方法、改进方法和改进方法且宽间隔处理产生的跳频序列分别进行预测。表6仅给出N=1 024，q=128，不同初始值时的混沌跳频序列的预测均方误差对比结果，其他情况下结果与之类似。由仿真结果可知，4种跳频序列均具备较强的抗预测能力，且本文方法较为优秀。

3 结束语

提出一种分段迭代的周期多比特重叠抽取算法来生成混沌跳频序列。首先将比特抽取法的一次性迭代转换成分段迭代，再产生混沌实值点并转换成二制小数，提高了跳频序列产生的实时性；然后对其进行周期多比特重叠抽取和非线性矩阵变换便可产生q元跳频序列，增加了跳频序列的复杂度；最后经过理论分析和仿真对比发现，相同条件下，改进方法产生的跳频序列在宽间隔处理前、后的性能和比特抽取法相当，所需平均迭代次数可减少约45% ，实时性大大改善。经实际验证，改进方法既能快速地产生实用的长周期码，又能适用于要求灵活更换跳频图谱的无线跳频通信系统。

表6 混沌跳频序列的预测均方误差(N=1 024,q=128)

[1] CHANDRA R. Competition and collaboration in cooperative coevolution of elman recurrent neural networks for time-series prediction[J]. IEEE Transactions on Neural Networks and Learning Systems,2015,26(12):3123-3136.[2] ZHAO Lifan, WANG Lu, BI Guoan, et al. Robust frequency hopping spectrum estimation based on sparse bayesian method[J]. IEEE Transactions on Wireless Communica tions, 2015, 14(2): 781-793.

[3] SADIKU M N O, MUSA S M, MOMOH O D. Cloud computing: opportunities and challenges[J]. IEEE Potentials, 2014, 33(1): 34-36.

[4] 凌聪, 孙松庚. Logistic映射跳频序列[J]. 电子学报, 1997, 25(10): 79-81. LING Cong, SUN Songgeng. Frequency-hopping sequences by the logistic map[J]. Acta Electronica Sinica, 1997, 25(10): 79-81.

[5] LING Cong, SUN Songgeng. Chaotic frequency hopping sequences[J]. IEEE Transactions on Communications, 1998, 46(11): 1433-1437.

[6] 凌聪, 孙松庚. 用于跳频码分多址通信的混沌跳频序列[J]. 电子学报, 1999, 27(1): 67-69. LING Cong, SUN Songgeng. Frequency-hopping sequences by chaotic maps for FH/CDMA communications[J]. Acta Electronica Sinica, 1999, 27(1): 67-69.

[7] 刘向东, 焉德军, 段晓东, 等. 中间多比特量化混沌跳频序列及其性能分析[J]. 微电子学与计算机, 2004, 21(8): 5-9. LIU Xiangdong, YAN Dejun, DUAN Xiaodong, et al. A chaotic frequency hopping sequences by mid multi-bit quantified and its properties[J]. Microelectronics and Computer, 2004, 21(8): 5-9.

[8] 米良, 唐刚. 一种混沌跳频序列构造方法[J]. 通信学报, 2005, 26(12): 69-74. MI Liang, TANG Gang. Design of frequency-hopping sequences based on chaotic map[J]. Journal on Communications, 2005, 26(12): 69-74.

[9] 王喜风, 王可人, 郭建蓬, 等. 基于耦合映象格子的宽间隔跳频序列的FPGA实现[J]. 重庆邮电大学学报: 自然科学版, 2011, 23(3): 281-287. WANG Xifeng, WANG Keren, GUO Jianpeng, et al. FPGA realization of wide-gap frequency hopping sequences based on coupled map lattice[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2011, 23(3): 281-287.

[10] 罗启彬, 张健. 一种新的混沌伪随机序列生成方式[J].电子与信息学报, 2006, 28(7): 1262-1265. LUO Qibin, ZHANG Jian. A new approach to generate chaotic pseudo-random sequence[J]. Journal of Electronics and Information Technology,2006,28(7):1262-1265.

[11] 胡英辉, 罗军, 苏辉. 一种改善混沌序列有限精度效应的新方法[J]. 系统仿真学报, 2012, 24(11): 2349-2352. HU Yinghui, LUO Jun, SU Hui. Novel method for improving finite precision effect of chaotic sequences[J]. Journal of System Simulation,2012,24(11):2349-2352.

[12] 许栋, 崔小欣, 王田, 等. 基于Logistic映射的混沌随机数发生器研究[J]. 微电子学与计算机, 2016, 33(2):1-6. XU Dong, CUI Xiaoxin, WANG Tian, et al. Research on chaotic pseudo random bit generator based on logistic map[J]. Microelectronics and Computer,2016,33(2):1-6.

[13] 李赞, 金力军, 常义林. 一种快速的跳频码序列产生方法[J]. 西安电子科技大学学报: 自然科学版, 2001,28(2):150-153. LI Zan, JIN Lijun, CHANG Yilin. A fast generation of frequency hopping sequences[J]. Journal of Xidian University:Natural Science Edition,2001,28(2):150-153.

[14] 何维苗, 冯冈. 构造宽间隔跳频码序列的两种算法之比较[J]. 解放军理工大学学报: 自然科学版, 2004, 5(4): 29-33. HE Weimiao, FENG Gang. Comparison of two algorithms to generate wide gap FH code sequence[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2004, 5(4): 29-33.

[15] VILLWOCK S, PACAS M. Application of the welchmethod for the identification of two-and three-masssystems[J]. IEEE Transactions on Industrial Electronics, 2008, 55(1): 457-466.

[16] GUAN Lei, LI Zan, SI Jiangbo, et al. Generation and characteristics analysis of cognitive-based highperformance wide-gap FH sequences[J]. IEEE Transactions on Vehicular Technology, 2015, 64(11): 5056-5069.

[17] CHUNG J H, YANG K. New classes of optimal low-hitzone frequency-hopping sequence sets by cartesian product[J]. IEEE Transactions on Information Theory, 2013, 59(1): 726-732.

[18] LI Zan, CAI Jueping, CHANG Yilin. Determining the complexity of FH/SS sequence by approximate entropy [J]. IEEE Transactions on Communications, 2009, 57(3): 812-820.

[19] CHEN Xiaojun, LI Zan, SI Jiangbo, et al. Determining the complexity of FH/SS sequences by fuzzy entropy [J]. IEEE International Conference on Communications,2011, 57(4): 1-5.

[20] 张家树, 肖先赐. 用于混沌时间序列自适应预测的一种少参数二阶Volterra滤波器[J]. 物理学报, 2001,50(7):1248-1254. ZHANG Jiashu, XIAO Xianci. A reduced parameter second-order volterra filter with application to nonlinear adaptive prediction of chaotic time series[J]. Acta Physica Sinica, 2001, 50(7): 1248-1254.

(编辑：魏琴芳)

The Key Laboratory of Science and Technology on Information Transmission and Dissemination in Communication Networks

Method for fast generating wide-gap chaotic frequency hopping sequences

XU Yao1, DAI Fusheng2, WANG Gang1
(1. School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, P.R. China;2. School of Information and Electrical Engineering, Harbin Institute of Technology at Weiha, Weihai 264209, P.R. China)

Aiming at the problem of poor real-time performance caused by the bit extraction method during the process of creating chaotic frequency hopping (FH) sequences, a new generation algorithm for chaotic FH sequences based on segmented iterative is proposed. The chaos mapping tracking real-value point obtained by segmented iterative is expressed as a binary decimal, and the wide interval sequence is generated by using the methods such as periodic multi-bit overlapping extraction, nonlinear matrix transformation and improved random shift replace algorithm. The simulation result shows that, under the premise that the balance properties, hamming correlation, FH interval, anti-prediction capacities and other FH sequence performances are not lower than the existing algorithms, the average number of iterations can be reduced by about 45%, and it also has the advantage on the aspects of real-time, storage footprint and the extended sequence period. Through verification, this algorithm is suitable for the wireless FH communication system that requests the flexible replacement of FH patterns.

wireless communication; FH sequences; chaos theory; wide interval map; long-period code

2016-05-30

2017-04-01 通讯作者：戴伏生 dfs1963@163.com

通信网信息传输与分发技术重点实验室基金

10.3979/j.issn.1673-825X.2017.03.006

TN924

A

1673-825X(2017)03-0320-07

许 尧(1993-)，男，山东枣庄人，博士研究生。研究方向为无线通信，联合信源信道编码等。E-mail: 1101698146@qq.com。 戴伏生(1963-)，男，教授，硕士生导师。研究方向为无线通信技术，通信电子系统及通信网等。E-mail:dfs1963@163.com。 王 钢(1962-)，男，教授，博士生导师。研究方向为通信网理论与技术，联合信源信道编码技术及无线数据传输技术等。