基于半导体量子点的量子通信
李 健,李登峰,朱家骥
(重庆邮电大学 理学院,重庆 400065)

基于半导体量子点的量子通信
李 健,李登峰,朱家骥
(重庆邮电大学 理学院,重庆 400065)
光子源和纠缠光子对的制备是量子信息产生和传输过程的源头,是实现量子通信的重要前提条件。半导体量子点固体系统具有可集成性和可扩展性的优点,并且与现有的半导体光电子学技术密切相关,近年来在单光子源和纠缠光子对制备方面取得了重要的进展,是未来全固态量子通信的重要元器件。从量子通信的基本原理出发,阐述了制备单光子源和纠缠光子对的重要性,介绍如何解析推导出圆形常规半导体量子点中的电子结构,描述了圆形拓扑绝缘体量子点中边缘态具有双重简并的电子结构,能级间隔与量子点的具体形状无关,并且具有自旋轨道锁定的特性,总结了实验和理论上在利用这一独特的电子结构制备单光子源和纠缠光子对方面取得的重要进展。
量子通信;量子点;单光子;纠缠光子对
0 引 言
量子通信引起人们广泛兴趣起始于1984年Bennett和Brassard提出BB84量子保密通信协议,经过三十多年的热烈研究,已经发展成为当今物理学和信息科学与工程的前沿研究热点,是量子力学和通信理论相结合的新兴研究领域。量子通信是指利用单光子、纠缠光子或连续变量体系加密携带量子比特进行信息传递的一种新型通讯方式。相对于经典通信而言,量子通信在理论上具有绝对的安全性和高效性。首先,量子通信在原理上可以实现无条件安全的信息传输,主要体现在量子加密的密钥是随机分发的,即使传输的量子态被窃取者截获,但如果无法得到正确的密钥,也无法破解信息;其次,在量子通信双方手中纠缠的2个粒子,由于量子力学的非局域性,当一个粒子的量子态发生变化时,另外一方的量子态就会随之立刻变化。而根据量子不可克隆原理,不存在一个能完美克隆2个非正交量子态的操作,窃听者所做的任何测量或干扰,都会立刻改变量子态,引起波函数的塌缩,从而引起误码率的明显上升,因此,测量接收到的纠缠光子的保真度就能确定通信是否被人窃听;最后,量子通信在原理上可以实现信息传输的高效性,由于传输的未知量子态在被测量之前会处于纠缠态,即处于多个状态的叠加态,例如一个量子态可以同时储存0和1这2个状态,10个这样的量子态就可以同时表示1 024个状态(2016年12月,潘建伟[1]研究小组在实验上制备出十光子纠缠态)。光量子通信的这样一次传输,就相当于经典通信方式的1 024次。可以想象,如果传输带宽是64位或者更高,那么效率的差别将十分惊人。量子通信不但在国家安全、金融等信息安全领域有着重大的应用价值和前景,而且在人们的日常生活领域也有很广泛的应用前景。图1是一种量子保密通信的原理框架图。
制备具有高确定度的单光子源和纠缠光子对是实现光量子密码(quantum cryptography)[2-3]、量子密钥传输(quantum key distribution)[4]、量子纠缠交换(quantum entanglement swap)[5]和量子存储(quantum memory)[6]的重要条件,是实现量子通信的基石。目前实验上制备单光子源和纠缠光子对的主要方案是基于冷原子系统[7-10],但冷原子系统不易大规模集成,要求非常低的温度条件;基于冷原子系统长程发送一个量子比特的信息所需时间在分钟量级以上,这大大限制了单光子器件的应用。加快传输速度有2种方案:①采用确定性单光子源,即利用单个原子发光,每次只发射一个光子;②利用多模式存储,即一次存储就可以存多个量子比特,选用固态系统制备单光子能够较好地解决上述困难。近年来,在基于半导体的量子信息方面取得了一系列具有标志性的进展,其中被称之为“人工原子”的零维半导体结构—半导体量子点,具有可集成性和可扩展性的优点,并且可与现有的半导体光电子学技术紧密结合,引起了科学界的广泛关注。本文主要介绍近年来取得重要进展的常规半导体量子点、拓扑绝缘体量子点中的电子结构,以及如何利用它们独特的电子结构制备单光子态及纠缠光子对。

图1 量子保密通信原理框图Fig.1 Quantum communication principle diagram
1 基于常规半导体量子点的量子通信

对于常见的自组装生长量子点,量子点中的电子在3个方向均受到限制,如图2所示。顶部和底部的门电极可以用来产生自旋轨道耦合效应并控制它的强度,量子点侧面的电极用来产生并调整横向限制势的强度。z方向可以近似用硬壁势来模拟,量子点平面可以近似用抛物限制势来模拟,由于z方向和垂直于z方向的电子运动无关,可以分离变量,z方向的厚度较小时,该方向运动的电子能量较高,在理论计算中若仅考虑低能电子的情况下,可以只考虑垂直于z方向平面的运动。
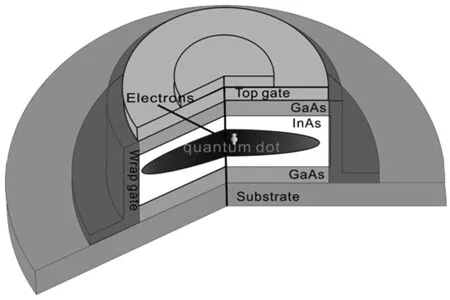
图2 单电子InAs量子点示意图Fig.2 Schematic diagram of the InAs quantum dot
在低能有效质量近似下,外磁场中单电子的哈密顿量可以写为
(1)

(2)
(3)
r2|n,m〉=(2n+|m|+1)|n,m〉
(4)
利用(2)—(4)式,抛物限制势下量子点中电子的本征方程为
H|n,m〉=((2n+|m|+1)ћω0+mћωL)|n,m〉=En,m|n,m〉,
(5)

量子点产生单光子示意图及其荧光光致发光谱如图3所示。其中,1X代表单个激子发光,2X代表双激子发光。图3b的内插图为单激子发光的二阶关联函数g2(τ),图3b取自文献[22]。对于外加垂直磁场为零的抛物限制势常规半导体量子点,导带底(能量Ec0=ћω)和价带顶(能量Ev0=-Eg-ћω)可以看作一个二能级系统,(见图3a),其中,Eg为构成量子点材料的能隙,ћω代表由于抛物限制势的存在,量子点中电子(空穴)能量的增加(降低)。在光学激发下,量子点吸收外部激发光的脉冲光子,电子可以从价带跃迁到导带;在电学激发下,也可以使量子点中电子从价带跃迁到导带。在上述2种情况下,若仅仅从价带中激发一个电子到导带上去,则会在价带中产生一个空穴,导带中的电子和价带中的空穴由于库仑吸引相互作用形成单激子(1X)。类似地,如果从价带激发2个电子到导带,导带中的2个电子和价带中的2个空穴由于库仑相互作用会形成双激子(2X)。不同激子的库仑相互作用不一样, 发射出的荧光光子能量也不一样,因此,实验上可以通过荧光峰来判断量子点中不同的激子态。基于这一原理,2000年A.Imamoglu领导的研究小组首次在InAs单量子点上观测到了具有单光子统计性质的光致荧光发射[22-23](见图3b),当量子点形成激子的时间小于量子点荧光的辐射寿命(~1 ns),量子点对应于每次激发,有且只会产生一个荧光光子,即可以产生单光子。图3b的内插图是实验测得的量子点中单激子激发荧光光谱的二阶相关函数,其中g2(0)<0.5,表明可以利用半导体量子点中特殊的电子结构制备出基于固态系统的单光子源。在随后的2005年,Yoshihisa Yamamoto等[24]在InAs单量子点上利用量子点中激子间的库仑相互作用制备得到特定偏振方向的单光子。除此以外,利用量子点中双激子跃迁制备纠缠光子对的物理机制也引起了广泛的兴趣,物理学家通过各种办法减小双激子到单激子转变的精细结构劈裂(fine-structure splitting,FSS)来制备纠缠光子对,如制备较高对称性的量子点[25-27],但是制备过程对实验设备和技术要求比较高,可以通过外加电场或磁场调控双激子精细结构劈裂[28-30],磁场调节的精确度比较高并且操作简单,还可以通过单轴应力场来调控双激子精细结构劈裂[31-33],应力场的优点是调节过程可逆,而且控制精细结构劈裂的精确度高,主要缺点是调节范围小。这些都是令人激动的研究途径,综合考虑,电场和磁场调节双激子精细结构劈裂的方法具有工艺简单,操作方便,是较为有效的调节方法。

图3 量子点产生单光子示意图及其荧光光致发光谱Fig.3 Schematic diagram of single photon generated by quantum dots and its photoluminescence spectra
虽然国内在半导体量子点研究方面起步比较晚, 但是在基于半导体量子点的单光子源和纠缠光子对制备方面却取得了一系列具有国际领先的原创性研究成果,2013年,潘建伟、陆朝阳[34]研究团队首次实现基于量子点脉冲共振荧光的确定性高品质单光子源,同时制备出全光学可调谐的量子点拉曼单光子源,实现了独立量子点之间的高对比度双光子干涉[35];中科大郭光灿、何力新[36]研究组通过研究双激子精细结构的产生机制,推导出了量子点中激子精细结构和偏振角在单轴应力下的唯象理论,并且给出了在外压下具有最小精细结构的量子点的简单判据。基于此方案,德国的Trotta[37-38]小组在实验上首次实现了可控的量子点纠缠光源。量子点纠缠光源原理及如何利用偏振分光镜将不同量子点发出的纠缠光子对级联如图4所示,图4取自文献[39]。2015年,郭光灿、何力新研究组在理论上证明了利用一组特殊的组合应力可以在大范围调节量子点发光能量的同时,将任意量子点的精细结构调节到接近于零(见图4a中的ΔFSS),这样基于量子点双激发的级联过程制备的纠缠光子对就解决了每个量子点的发光能量都不一样而无法实现可扩展量子点纠缠光源的关键困难,从而提出了一种可扩展、确定性的量子点纠缠光源方案,该方案可以构建基于半导体量子点的全固态量子中继器(见图4b)[39]。这些研究成果为基于常规半导体量子点确定性纠缠光源的实用化铺平了道路。
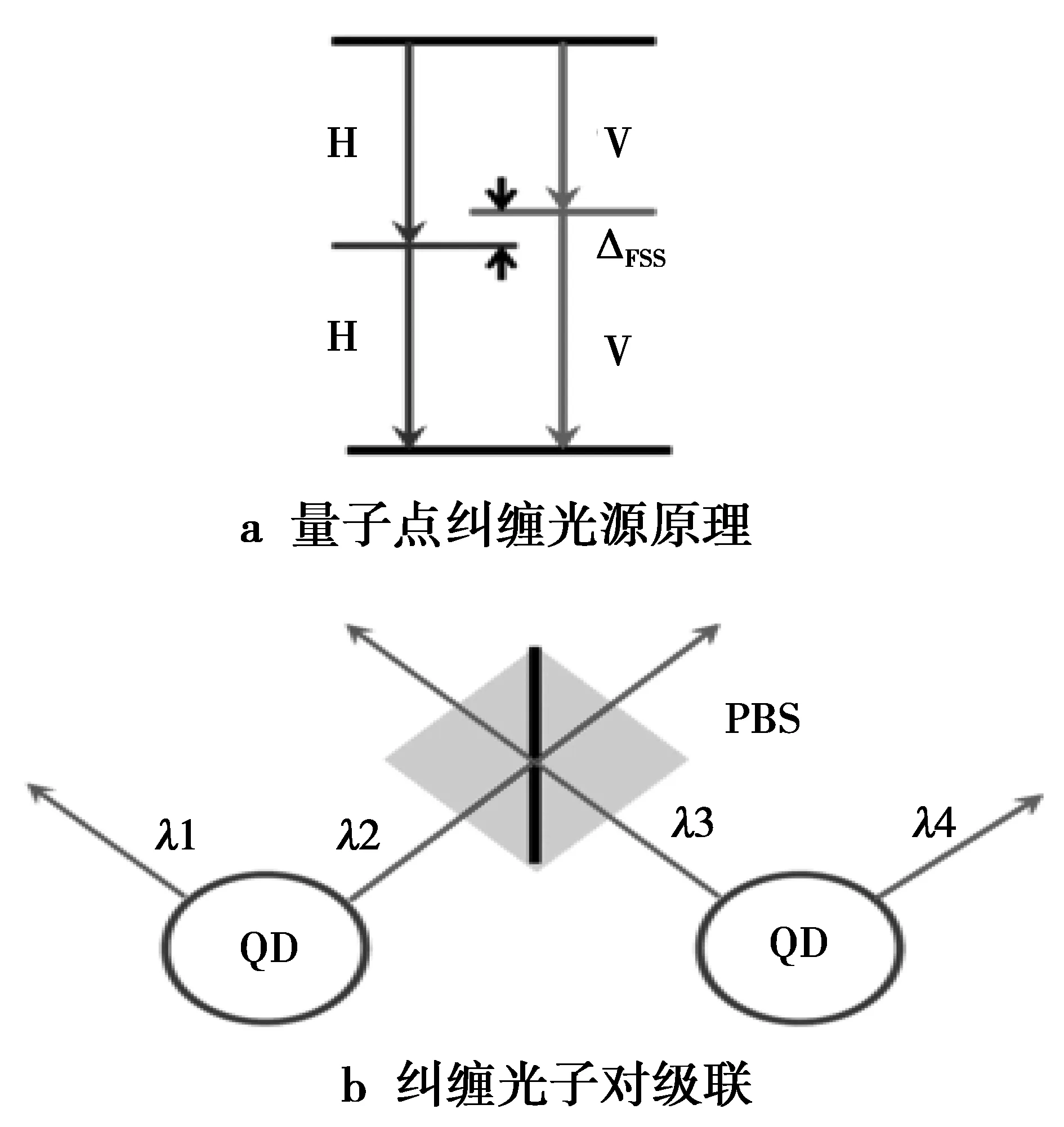
图4 量子点纠缠光源原理及如何利用偏振分光镜将不同量子点发出的纠缠光子对级联示意图Fig.4 Principle of quantum dot entangled light source and how to use the polarizing beam splitter to represent the entangled photons of different quantum dots
2 基于拓扑绝缘体量子点的量子通信

(6)

(7)

圆形和椭圆形量子点的能谱及其基态电子几率分布如图5所示。数值得到的能谱见图5左边,其中,空心圆(实心圆)表示边缘态(体内态)的能谱。而空心正方形(实心正方形)表示椭圆形量子点边缘态(体内态)的能谱,圆形表示圆形量子点,方形表示椭圆形量子点(形变为δ=2),量子点的周长为P=2π×30 nm,该能谱中包含边缘态和体内态。可以发现,边缘态的能谱与量子点的形状无关,而且是等间隔分布的,拓扑绝缘体量子点基态的电子分布在量子点的边缘上。
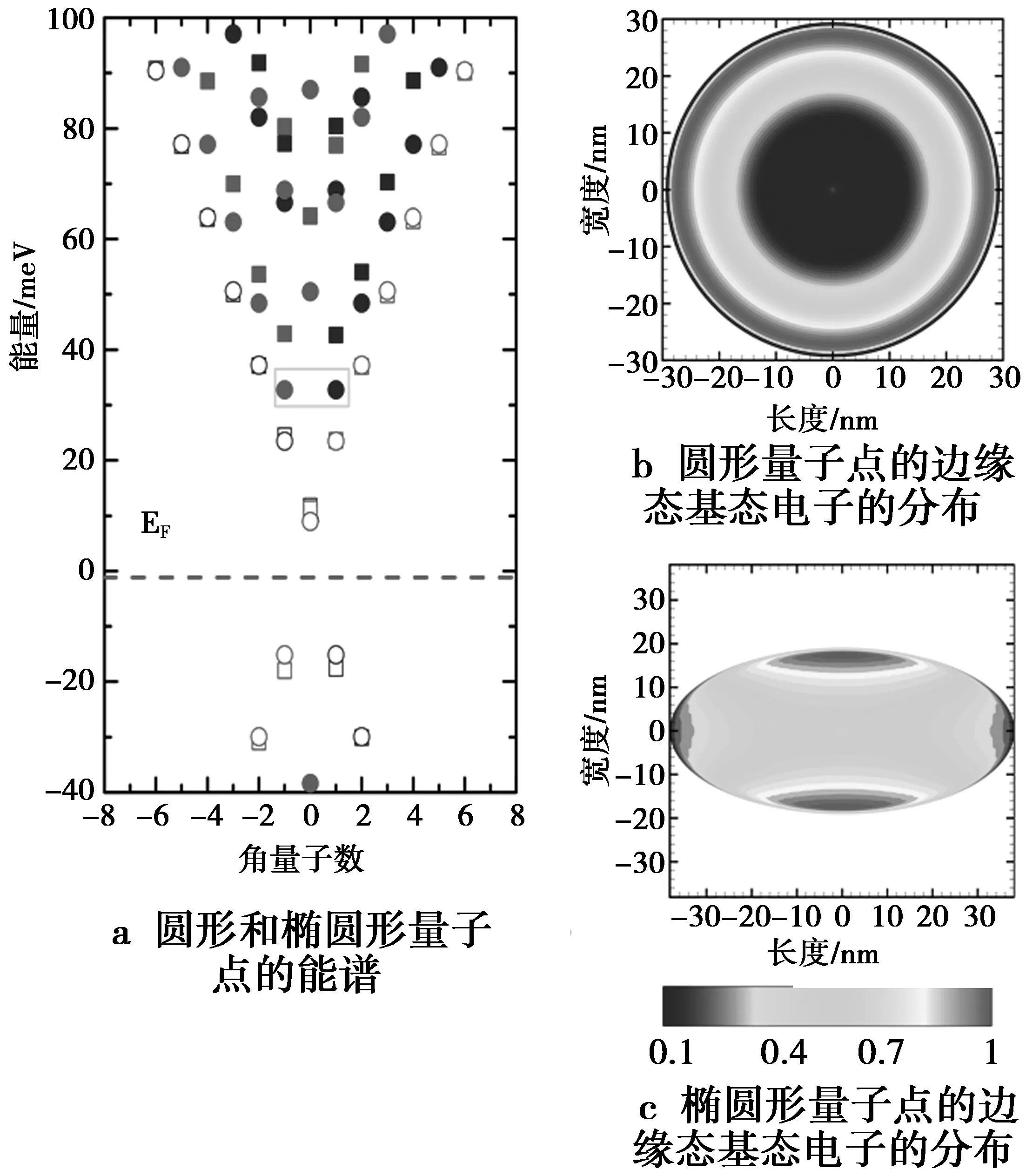
图5 圆形和椭圆形量子点的能谱及其基态电子几率分布Fig.5 Energy spectrum and density distributions of the lowest conduction band electron states for circular and elliptical quantum dots respectively
为了更清晰地给出拓扑绝缘体量子点中电子结构的特征,常凯等[44]给出边缘态电子的解析表达式。哈密顿量(6)式中各项的物理含义十分清晰,其中,含D的项反映了电子空穴能谱的对称性(particle-hole symmetry),含C的项决定了零点能的偏移,对能谱的整体特征没有影响,为方便起见,在推导中取C=0。假设量子点的边缘态存在如下解
Ψ=eλ(ρ-R)[eimφ,ei(m+1)φ]T
(8)
带入薛定谔方程HΨ=EΨ,则有
(9)
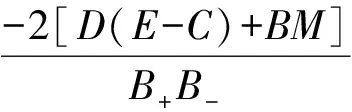


(10)
从边缘态的解析表达式可以发现,在硬壁势圆盘量子点中边缘态能级间隔为

(11)

3 总结与展望
量子通信是当今物理学和信息科学与工程的前沿研究热点,量子通信的实现离不开单光子和纠缠光子对的制备,半导体量子点具有可集成性和可扩展性等多方面的优点,其独特的能级结构非常适用于制备单光子源和纠缠光子对。基于传统半导体量子点的单光子源方案已经在单量子点系统中实现,如何实现纠缠光子对在理论上亦有所突破,如何在传统半导体量子点中实现大规模、集成化的单光子源和纠缠光子对是下一步的研究重点。此外,拓扑绝缘体量子点具有本征的自旋动量锁定等新奇的拓扑性质,理论提出了一些纠缠光子对的实现方案,实验上也已成功制备出了三维拓扑绝缘体量子点,如何利用其新奇的拓扑性质在实验中制备出高质量的单光子源和纠缠光子对是一个方兴未艾的热门研究方向。此外,随着二维材料的热烈研究,基于过渡金属硫族化合物、黑磷等单层材料量子点制备单光子源和纠缠光子对也是一个重要的研究方向。综上所述,基于半导体量子点等固态系统的量子通信技术有望成为推动量子通信技术在大规模应用与产业化方面的关键技术,值得我们继续跟踪和深入研究。
[1] WANG X L, CHEN L K, LI W, et al. Experimental ten-photon entanglement[J]. Physical review letters,2016,117(21): 210502-1-210502-6.
[2] BENNETT C H. Quantum cryptography using any two nonorthogonal states[J]. Physical review letters, 1992, 68: 3121-3124.
[3] EKERT A K.Quantum cryptography based on Bell’s theorem[J].Physical review letters,1991,67(6):661-663.
[4] SHOR P W, PRESKILL J.Simple proof of security of the BB8 4 quantum key distribution protocol[J].Physical review letters,2000,85(2): 441-444.
[5] PAN J W, BOUWMEESTER D, WEINFURTER H, et al. Experimental Entanglement Swapping: Entangling Photons That Never Interacted[J].Physical review letters,1998,80(18): 3891-3894.
[6] LVOVSKY A I, SANDERS B C, TITTEL W. Optical quantum memory[J].Nature Photonics, 2009, 3(12): 706-714.
[7] MONROE C.Quantum information processing with atoms and photons[J].Nature,2002, 416(6877): 238-246.
[8] DARQUIé B, JONES M P A, DINGJAN J, et al. Controlled single-photon emission from a single trapped two-level atom[J].Science(New York,N. Y.), 2005, 309(5733): 454-456.
[9] MOLINA-TERRIZA G, TORRES J P,TORNER L. Twisted photons[J].Nature Physics,2007,3(5): 305-310.
[10] 郭光灿.量子信息技术[J].重庆邮电大学学报:自然科学版, 2010, 17(5): 521-525. GUO Guancan.Quantum information technology[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2010, 17(5): 521-525.
[11] ZRENNER A,BUTOV L V,HAGN M,et al. Quantum dots formed by interface fluctuations in AlAs/GaAs coupled quantum well structures[J]. Physical review letters, 1994, 72(21): 3382-3385.
[12] SAKAKI H,YUSA G,SOMEYA T,et al. Transport properties of two-dimensional electron gas in AlGaAs/GaAs selectively doped heterojunctions with embedded InAs quantum dots[J].Applied physics letters,1995,67(23): 3444-3446.
[13] ELLINGSON R J, BEARD M C, JOHNSON J C, et al. Highly efficient multiple exciton generation in colloidal PbSe and PbS quantum dots[J].Nano letters, 2005, 5(5): 865-871.
[14] DAVID L K, PAUL L. M, JANET E B K, et al. An approach to electrical studies of single nanocrystals[J]. Applied Physics Letters,1996, 68(18):2574-2576.
[15] KOUWENHOVEN L P,AUSTING D G,TARUCHA S. Few-electron quantum dots[J]. Reports on Progress in Physics,2001, 64(6):701-736.
[16] IAFRATE G J,HESS K,KRIEGER J B,et al. Capacitive nature of atomic-sized structures[J]. Physical Review B,1995,52(15):10737-10739.
[17] TARUCHA S, AUSTING D G, HONDA T, et al. Shell Filling and Spin Effects in a Few Electron Quantum Dot[J].Physical review letters, 1996, 77(17): 3613-3616.
[18] KOUWENHOVEN L P, OOSTERKAMP T H, DANOESASTRO M W S,et al.Excitation spectra of circular, few-electron quantum dots[J]. Science (New York, N.Y.),1997,278(5344): 1788-1792.
[19] AUSTING D G, SASAKI S, TARUCHA S, et al. Ellipsoidal deformation of vertical quantum dots[J].Physical Review B,1999,60(16): 11514-11523.
[20] EZAKI T, MORI N, HAMAGUCHI C. Electronic structures in circular, elliptic, and triangular quantum dots[J]. Physical Review B, 1997, 56: 6428-6431.
[21] FOCK V.Bemerkung zur Quantelung des harmonischen Oszillators im Magnetfeld[J]. Zeitschrift für Physik A Hadrons and Nuclei, 1928, 47(5): 446-448.
[22] MICHLER P, KIRAZ A, BECHER C, et al. A quantum dot single-photon turnstile device[J]. Science, 2000, 290(5500): 2282-2285
[23] MICHLER P, IMAMOGLU A, MASON M D, et al. Quantum correlation among photons from a single quantum dot at room temperature[J]. Nature, 2000, 406(6799): 968-970;
[24] SANTORI C, PELTON M, SOLOMON G, et al. Triggered single photons from a quantum dot[J]. Physical review letters, 2001, 86(8): 1502-1505.
[25] MOHAN A, FELICI M, GALLO P, et al. Polarization-entangled photons produced with high-symmetry site-controlled quantum dots[J]. Nature Photonics, 2010, 4(5): 302-306.
[26] SINGH R, BESTER G. Nanowire quantum dots as an ideal source of entangled photon pairs[J]. Physical review letters,2009,103(6): 063601-1-063601-4.
[27] JUSKA G, DIMASTRODONATO V, MERENI L O, et al.Towards quantum-dot arrays of entangled photon emitters[J].Nature Photonics, 2013, 7(7): 527-531.
[28] BENNETT A J, POOLEY M A, STEVENSON R M, et al. Electric-field-induced coherent coupling of the exciton states in a single quantum dot[J]. Nature Physics, 2010, 6(12): 947-950.
[29] STEVENSON R M, YOUNG R J, ATKINSON P, et al. A semiconductor source of triggered entangled photon pairs[J].Nature,2006, 439(7073): 179-182.
[30] HUDSON A J, STEVENSON R M, BENNETT A J, et al. Coherence of an entangled exciton-photon state[J].Physical review letters, 2007, 99(26): 266802-1-266802-4.
[31] KUKLEWICZ C E, MALEIN R N E, PETROFF P M, et al.Electro-elastic tuning of single particles in individual self-assembled quantum dots[J].Nano letters, 2012, 12(7): 3761-3765.
[32] TROTTA R, ZALLO E, ORTIX C, et al. Universal recovery of the energy-level degeneracy of bright excitons in InGaAs quantum dots without a structure symmetry[J].Physical review letters,2012,109(14):147401-1-147401-5.
[33] TROTTA R, MARTíN-SáNCHEZ J, DARUKA I, et al. Energy-tunable sources of entangled photons: a viable concept for solid-state-based quantum relays[J].Physical review letters,2015,114(15): 150502-1-150502-5.
[34] HE Y M,HE Y,WEI Y J,et al.On-demand semiconductor single-photon source with near-unity indistinguishability[J].Nature nanotechnology,2013,8(3):213-217.
[35] HE Y, HE Y M,WEI Y J,et al.Indistinguishable tunable single photons emitted by spin-flip Raman transitions in InGaAs quantum dots[J]. Physical review letters,2013,111(23): 237403-1-237403-5.
[36] GONG M, ZHANG W, GUO G C, et al. Exciton polarization, fine-structure splitting, and the asymmetry of quantum dots under uniaxial stress[J]. Physical review letters,2011,106(22): 227401-1-227401-4.
[37] TROTTA R, ZALLO E,ORTIX C, et al. Universal recovery of the energy-level degeneracy of bright excitons in InGaAs quantum dots without a structure symmetry[J]. Physical review letters, 2012, 109(14): 147401-1-147401-5.
[38] TROTTA R, WILDMANN J S, ZALLO E, et al. Highly entangled photons from hybrid piezoelectric-semiconductor quantum dot devices[J]. Nano Letters,2014,14(6): 3439-3444.
[39] WANG J, GONG M, GUO G C, et al. Towards scalable entangled photon sources with self-assembled InAs/GaAs quantum dots[J]. Physical review letters, 2015, 115(6): 067401-1-067401-5.
[40] KANE C L, MELE E J. Quantum spin hall effect in graphene[J].Physical review letters,2005,95(22):226801-1-226801-4.
[41] BERNEVIG B A, HUGHES T L, ZHANG S C. Quantum spin hall effect and topological phase transition in HgTe quantum wells[J].Science, 2006, 314(5806): 1757-1761.
[42] KONIG M, WIEDMANN S, BRUNE C, et al. Quantum spin hall insulator state in HgTe quantum wells[J].Science(New York,N.Y.), 2007, 318(5851): 766-770.
[43] HINZ J, BUHMANN H, SCHAFER M, et al. Gate control of the giant rashba effect in HgTe quantum wells[J]. Semicond Sci and Techno, 2006, 21(4): 501-506.
[44] CHANG K, LOU W K. Helical quantum states in HgTe quantum dots with inverted band structures[J].Physical review letters, 2011, 106(20): 206802-1-206802-4.
[45] LI J, LOU W K, ZHANG D, et al.Single-and few-electron states in topological-insulator quantum dots[J]. Physical Review B,2014, 90(11): 115303-1-115303-7.
[46] XIN X, ZHOU D. Kondo effect in a topological insulator quantum dot[J].Physical Review B, 2015, 91(16): 165120-1-165120-13.
[47] EZAWA M. A topological insulator and helical zero mode in silicene under an inhomogeneous electric field[J]. New Journal of Physics, 2012, 14(3): 33003-33013.
[48] JIA G Z, LOU W K, CHENG F, et al. Excellent photothermal conversion of core/shell CdSe/Bi2Se3quantum dots[J]. Nano Research, 2015, 8(5): 1443-1453.
[49] JIA G, WANG P, WU Z, et al. Formation of ZnSe/Bi2Se3QDs by surface cation exchange and high photothermal conversion[J]. AIP Advances, 2015, 5(8): 087176-1-087176-7.
(编辑:王敏琦)
s:The National Natural Science Foundation of China (11604036, 11404043); The Chongqing Fundamental, Frontier Research Program (cstc2016jcyjA0208); The Foundation of Education Committees of Chongqing (KJ1600420)
Quantum communication based on semiconductor quantum dots
LI Jian,LI Dengfeng,ZHU Jiaji
(School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065,P.R. China)
The preparation of single photon sources and entangled photon pairs is the key to generation and transmission of quantum information, which is also an important prerequisite for quantum communication. Semiconductor quantum dot with high integration and expansion, closely related with the recently semiconductor optoelectronics technology, has made great progress in recent years for the preparation of single photon sources and entangled photon pairs, which must be an important component of solid state quantum communication in the future. In this review, we introduce the basic principles of quantum communication and explain the significance of design and implementation of single photon sources and entangled photon pairs with quantum dot. The electronic structures of conventional semiconductor quantum dots and topological insulator quantum dots are discussed, especially the electronic structure of the edge states in a circular topological insulator quantum dot has a double degeneracy, the electronic structures are independent of the shape of the quantum dot, and show spin-angular momentum locking. Finally, we present how to take advantage of the electronic structure of quantum dot for the preparation of single photon sources and entangled photon pairs, and great progress has been achieved in this field.
quantum communication; quantum dot; single photons; entangled photon pairs
10.3979/j.issn.1673-825X.2017.03.001
2017-03-14
2017-05-04 通讯作者:李 健 jianli@cqupt.edu.cn
国家自然科学基金(11604036, 11404043);重庆市科委一般项目(cstc2016jcyjA0208);重庆市教委科学与技术研究项目(KJ1600420)
TN911;O431.2
A
1673-825X(2017)03-0285-08

李 健(1986-),男,四川绵阳人,讲师,博士,研究方向为拓扑绝缘体等新型二维材料半导体量子点中的电子结构,激子物理性质及其在纠缠光子态等方面的应用。E-mail:jianli@cqupt.edu.cn。

李登峰(1977-),男,四川阆中人,教授,博士,研究方向为新型二维材料的电学和输运性质研究,半导体量子点的输运性质研究。E-mail:lidf@cqupt.edu.cn。

朱家骥(1980-),男,安徽淮南人,教授,博士,研究方向为拓扑绝缘体和新型二维材料的磁性与自旋电子学,基于半导体低维结构的量子计算与量子通信等研究。E-mail:zhujj@cqupt.edu.cn。

