基于特征线法的A-Line模型的误差分析与研究

刘 欣，王志峰，梁贵书

(华北电力大学 电气与电子工程学院，河北 保定 071003)



基于特征线法的A-Line模型的误差分析与研究

刘 欣，王志峰，梁贵书

(华北电力大学 电气与电子工程学院，河北 保定 071003)

传输线模型是电力系统电磁暂态计算的重要组成部分，近几年的研究中提出了几种新的模型，其中A-Line模型是一种基于特征线法的双诺顿模型，相比于J. Marti和ULM模型，由于其计算过程中不需要对传播常数进行拟合，使架空线暂态计算更为简单。然而，该模型在处理频变参数的时域卷积计算中，采用端口电流代替沿线电流，将会产生一定的误差，且该误差与线路参数密切相关，然而现有文献并没有对该模型进行详细的误差分析和适用范围研究。通过对A-Line模型进行特征阻抗和传播常数误差公式推导及线路参数对特征阻抗和传播常数影响的讨论，对A-Line模型的误差及适用范围进行了分析，并通过算例验证了所得分析结论的正确性，为该模型的工程应用提供了理论依据。

传输线；A-Line模型；特征线法；卷积计算；误差分析

0 引 言

作为电力系统重要组成部分，传输线计算模型得到了国内外学者的广泛研究。较为著名的频变参数传输线计算模型有J. Marti[1,2]和ULM[3]模型，其中J. Marti模型在EMTP中得到了广泛应用。近几年针对以上模型的研究主要集中于解决模型的不稳定性和无源性问题[4,5]，以及提高模型的精度[6,7]。同时，在文献[8,9]中介绍了传输线的Bergeron模型，利用特征线法(MOC)[10-12]，经过一定的转换，把分布参数的传输线等值为电阻性网络。文献[13,14]中介绍了FDTD法，应用一阶中心差分公式，对时域偏微分方程进行离散，并结合端部条件进行数值求解。

近几年针对传输线时域计算提出了一些新型计算模型， DEPACT(Delay Extraction-based Passive Compact Transmission-line Macromodeling Algorithm)[15,16]方法结合MOC和矩阵有理逼近(MRA)[17,18]方法对传输线进行延时提取，将传输线分为有损和无损部分，然后进行有效求解，并且文献中对该方法进行了准确的误差分析。文献[19]基于特征线法提出了一种新型多导体架空线时域计算双诺顿模型(A-Line模型)，该模型方法考虑了大地阻抗，并且不需要对传播常数进行拟合，使计算更加简便。但是该模型的推导过程中，在进行卷积运算时用端口电流代替了沿线电流，将会产生一定的误差。现有文献并没有对该模型的误差进行分析，没有给出其具体适用范围，为以后模型的应用带来不便。

本文通过对文献[19]模型的传输参数频域公式推导，得出了该模型下传输线的特征阻抗和传播常数误差公式，并对特征阻抗和传播常数进行了误差分析，直观地反映出了计算结果幅值以及相速度的误差情况。根据分析结果得出了该模型的适用范围，为该模型的有效应用提供了理论基础。

1 A-Line模型回顾

传输线频域电报方程为

(1a)

(1b)

其中

(2)

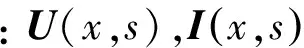
式(1)转化为时域形式为

(3a)

(3b)

式(3a)中⊗代表卷积计算。

基于特征线法(如图1所示)、后向欧拉公式、矢量匹配以及递归卷积数值算法，经推导可得传输线方程端口方程为[19]

(4a)

(4b)

其中

(5a)

(5b)

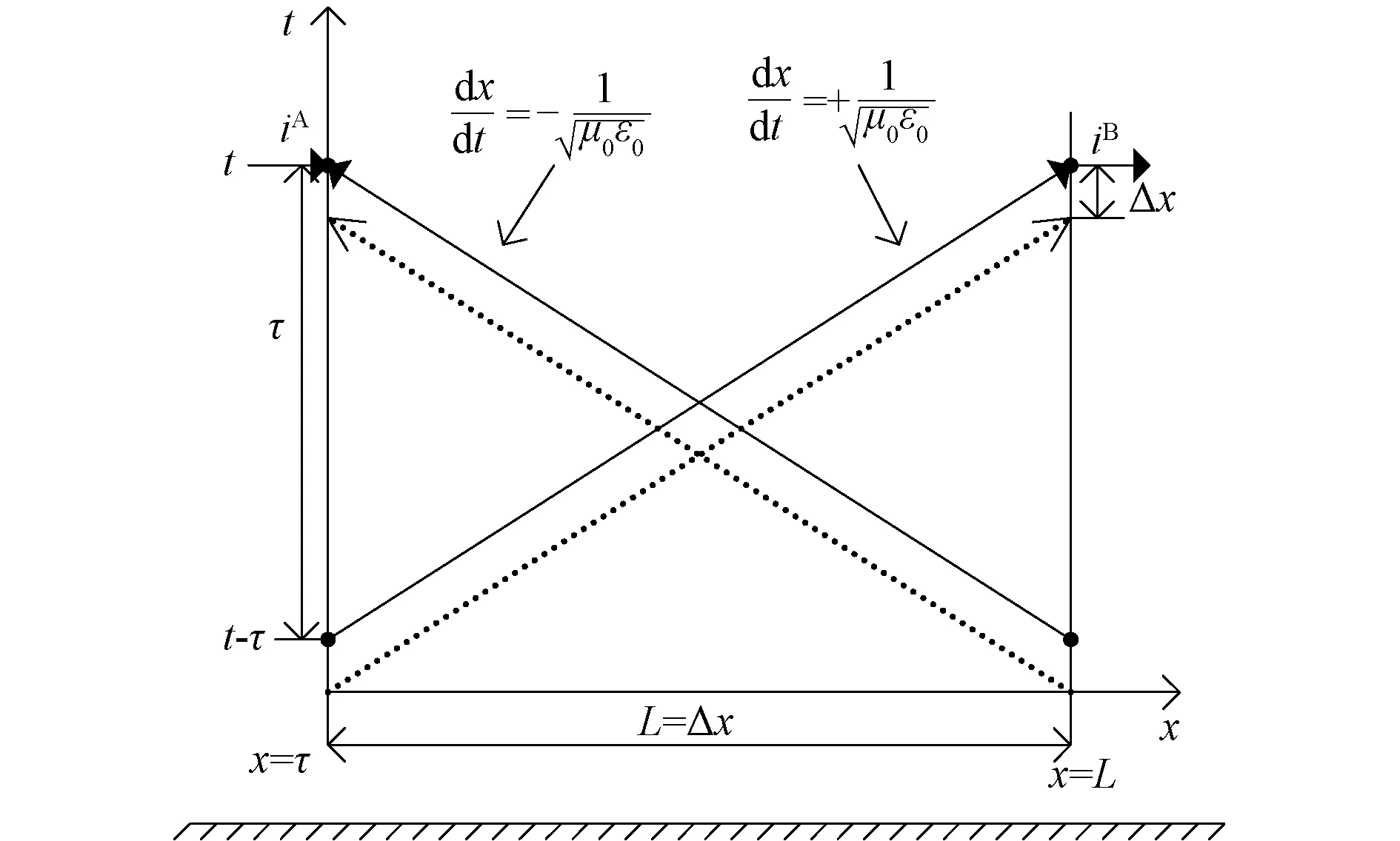
图1 A-Line模型特征曲线Fig.1 Characteristics curves of A-Line model

根据式(4a)～(5b)可以得到A-Line模型的双诺顿电路，如图2所示。

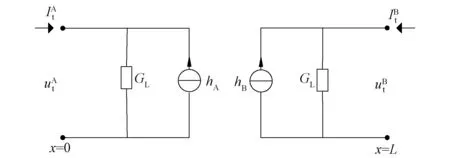
图2 A-Line双诺顿模型电路Fig.2 Dual Norton circuit for A-Line model

2 A-Line模型误差分析

2.1 传输线特征阻抗和传播常数误差公式推导

对于无损多导体传输线，特征阻抗定义如下

(6)

式中：μ0和ε0分别为真空磁导率和介电常数；P为麦克斯韦电位系数矩阵。

将式(6)左乘式(3b)，然后和式(3a)分别进行加减运算，可得

(7a)

(7b)

根据图1的特征曲线可将式(7)改写为

(8a)

(8b)

其中式(8a)和式(8b)分别对应正向特征线和反向特征线。

对式(8a)和式(8b)采用后向欧拉公式，并进行拉普拉斯变换，可得到如下频域方程

(9a)

(9b)

其中l为导线首末端对应的长度。

由此可得A-Line模型的传输参数矩阵为

(10)

根据文献[20]可知，电报方程频域解析方法中的传输参数矩阵为

(11)

其中特性阻抗和传播常数矩阵为

(12)

(13)

结合式(10)、(11)可得A-Line模型的特征阻抗和传播常数为

(14)

(15)

利用二范数分别定义特征阻抗和传播常数的误差公式为

(16)

(17)

特征阻抗影响传输线计算幅值，相速度与传播常数的虚部成反比，所以通过对特征阻抗和传播常数的误差分析可以直观有效的反映出计算值的误差情况。

2.2 误差分析

本节通过以上推导的误差公式对影响模型误差的主要因素(频率、导线长度、大地电阻率以及导线高度)进行分析。导线高度取10 m，空气磁导率为μ0=4π×10-7H/m，空气介电常数为ε0=8.854×10-12F/m，大地相对磁导率为μr=1，大地相对介电常数取εr=10。大地电阻率分别取100Ω·m和1 000Ω·m时特征阻抗误差随频率和导线长度变化分别如图3(a)，(b)所示。

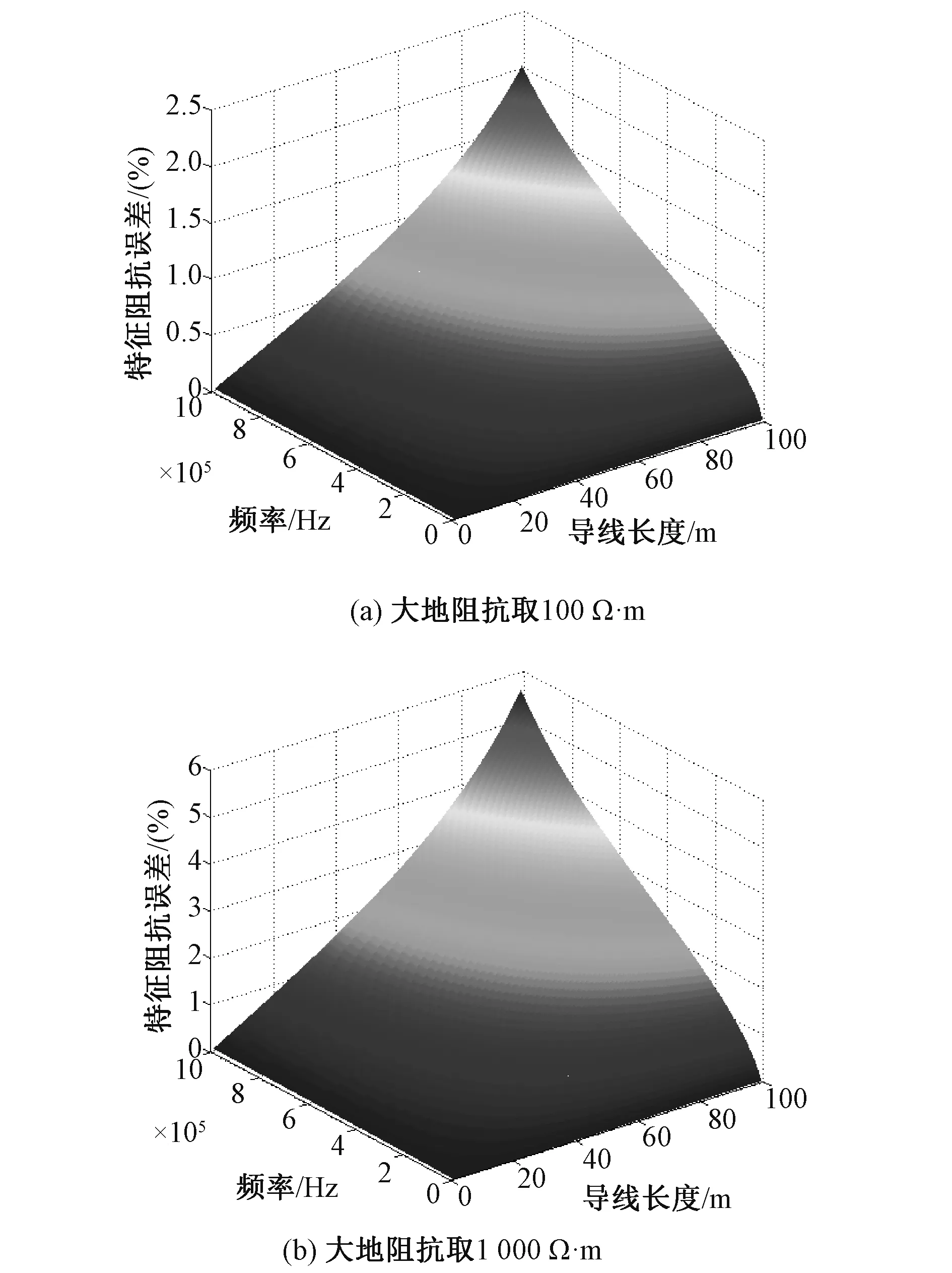
图3 特征阻抗误差随频率和导线长度变化图Fig.3 Error variation of characteristic impedance with frequency and line length

频率取50Hz和1MHz时，特征阻抗误差随导线长度和大地电阻率变化分别如图4(a)、(b)所示。

导线长度分别取100m和1 000m时，特征阻抗误差随频率和大地电阻率变化分别如图5(a)、(b)所示。

对图3，图4和图5进行分析可知，A-Line模型特征阻抗的误差随频率，导线长度和大地电阻率的增大而增大。

导线长度取100m时，传播常数误差随频率和大地电阻率变化情况如图6所示。

大地电阻率取100Ω·m时，传播常数误差随频率和导线长度变化情况如图7所示。

频率取1MHz时，传播常数误差随大地电阻率和导线长度变化情况如图8所示。

对图6～8进行分析可知，传播常数误差随频率、导线长度以及大地电阻率的增大而增大。

频率取1MHz，导线长度取100m时，特征阻抗和传播常数误差随导线高度变化如图9-10所示。

对图9和图10进行分析可知，特征阻抗以及传播常数误差随着导线高度的增大而减小。

通过以上误差分析可知A-Line模型具有一定的适用范围，当超出适用范围时将会产生较大误差。对适用性进行分析时需要综合考虑频率、导线长度、大地电阻率以及导线高度的影响，当频率和大地电阻率较大时，为了保证较小的误差，导线长度只能取较小值。而当频率和大地电阻率较小时，导线长度可以取到较大值。同时，当线路较高时适用范围会有所扩大。

表1和表2分别给出了导线高度取10m，误差保证在5% 以下，大地电阻率分别取100Ω·m和1 000Ω·m时导线长度随频率的变化情况。

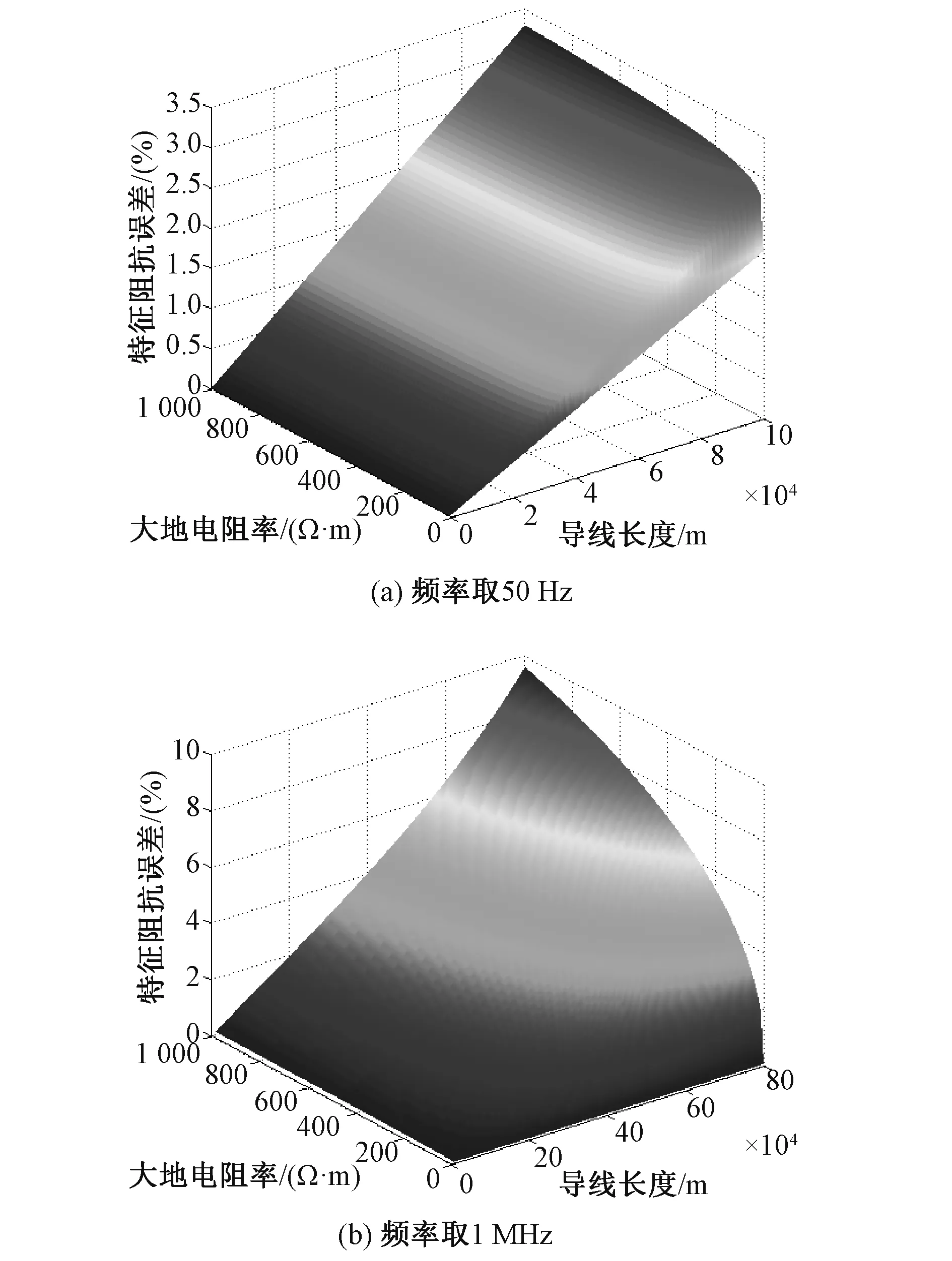
图4 特征阻抗误差随导线长度和大地电阻率变化图Fig.4 Error variation of characteristic impedance with line length and earth resistivity

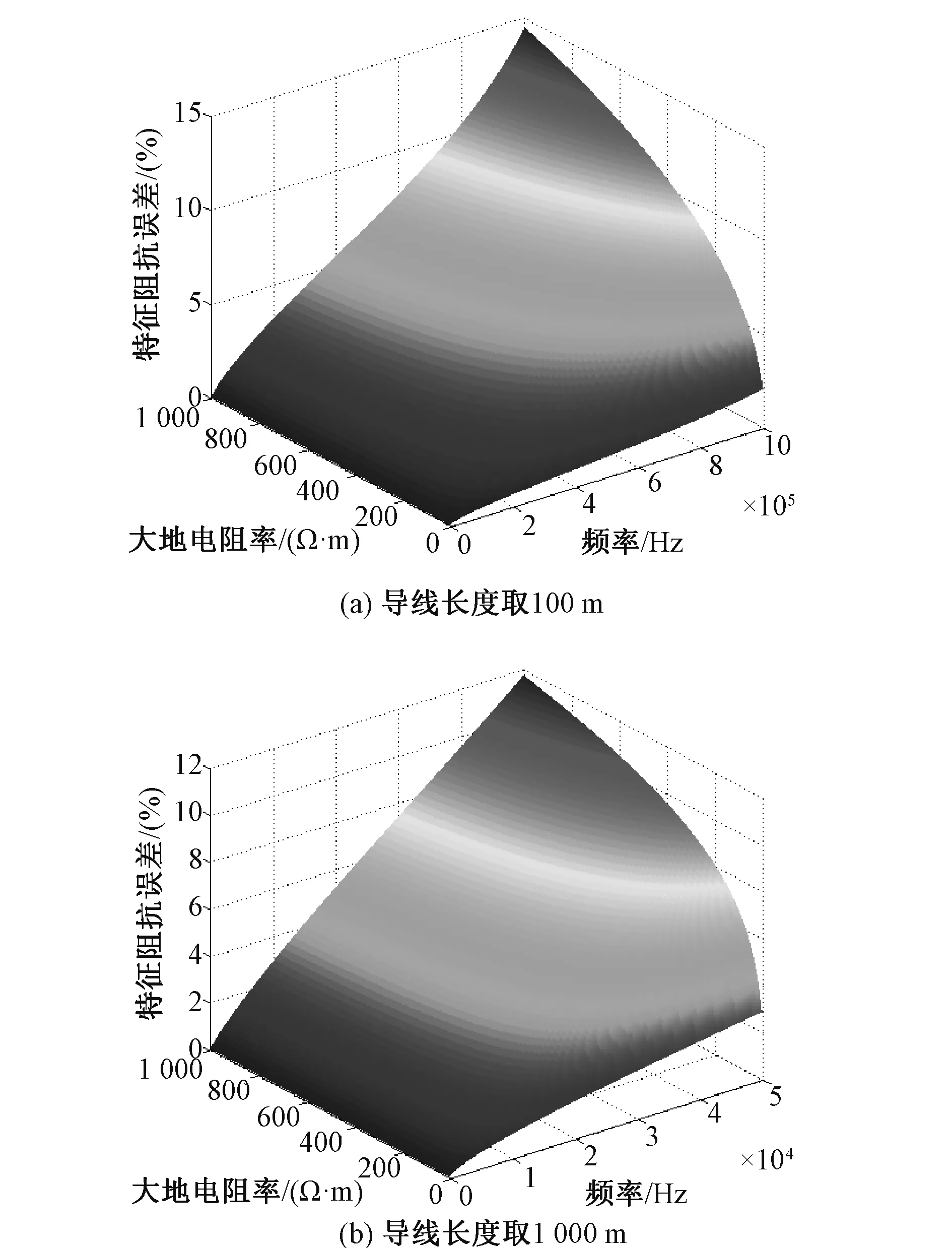
图5 特征阻抗误差随频率和大地电阻率变化图Fig.5 Error variation of characteristic impedance with frequency and earth resistivity

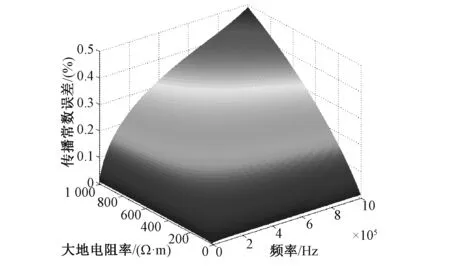
图6 传播常数误差随频率和大地电阻率变化图Fig.6 Error variation of propagation parameter with frequency and earth resistivity

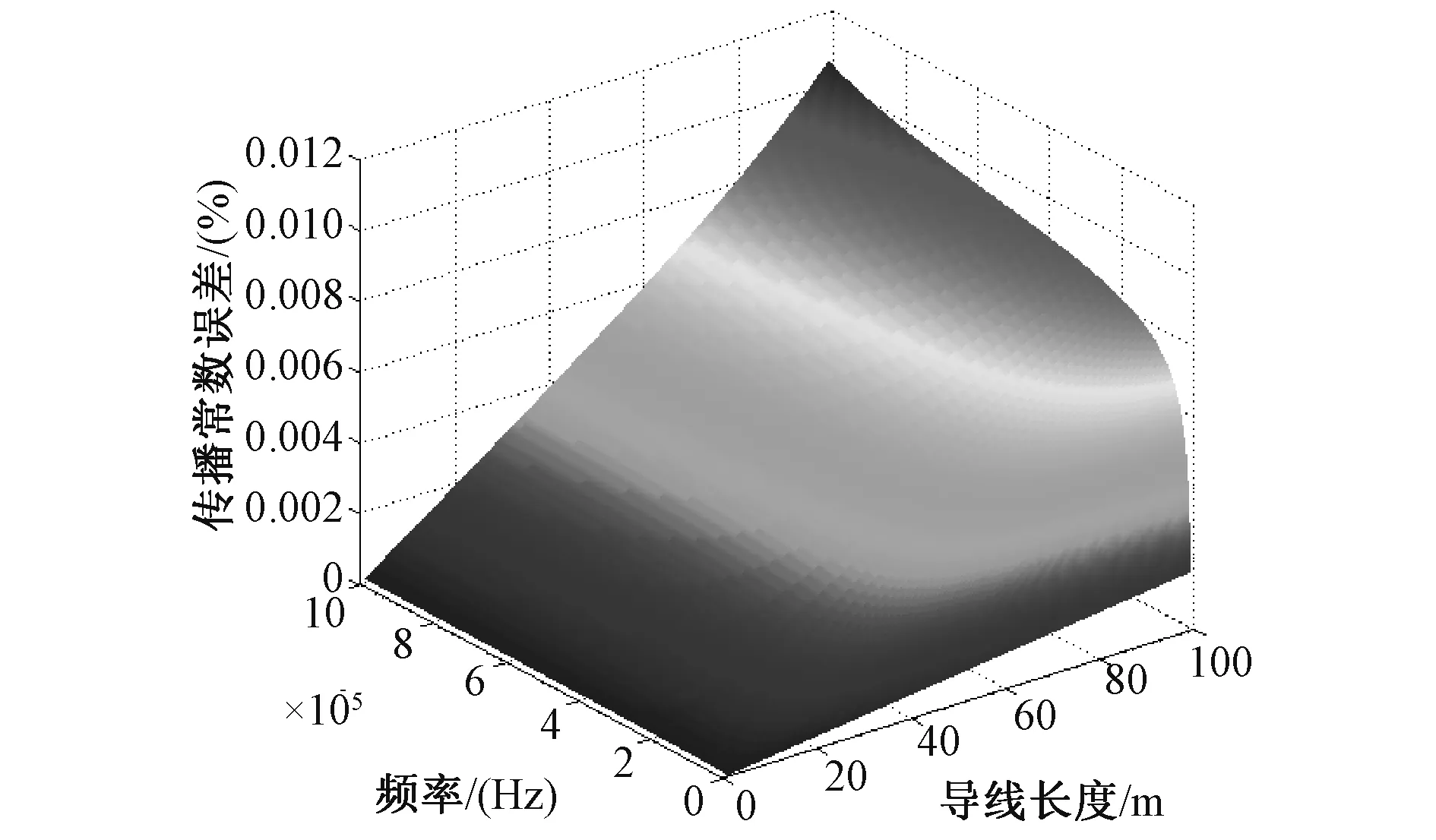
图7 传播常数误差随频率和导线长度变化图Fig.7 Error variation of propagation parameter with frequency and line length

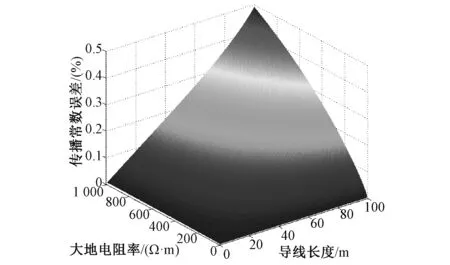
图8 传播常数误差随大地电阻率和导线长度变化图Fig.8 Error variation of propagation parameter with earth resistivity and line length

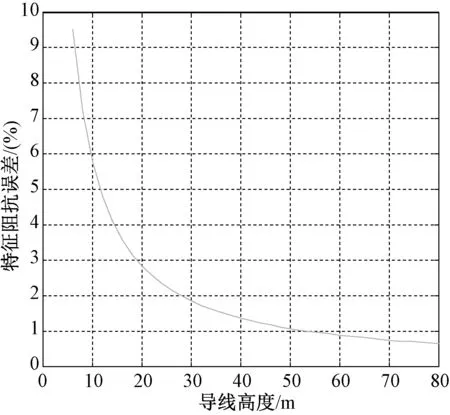
图9 特征阻抗误差随导线高度变化图Fig.9 Error variation of characteristic impedance with line height

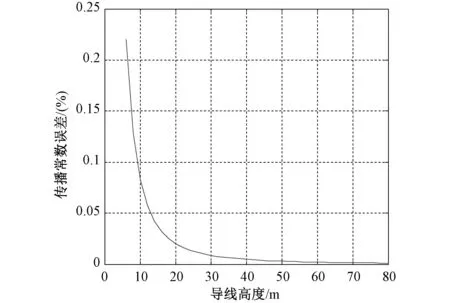
图10 传播常数误差随导线高度变化图Fig.10 Error variation of propagation parameter with line height

Tab.1 Variation of conductor length with frequency when earth resistivity is 100 Ω·m

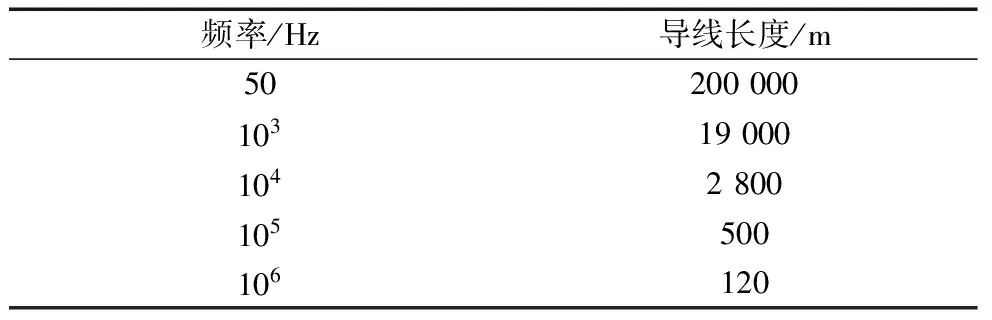
频率/Hz导线长度/m50200000103190001042800105500106120

表2 大地电阻率取1 000 Ω·m导线长度随频率变化情况Tab.2 Variation of conductor length with frequency when earth resistivity is 1 000 Ω·m

3 算 例

3.1 单导体传输线

本例及后面的算例都采用A-Line方法和频域解析方法进行计算比较。

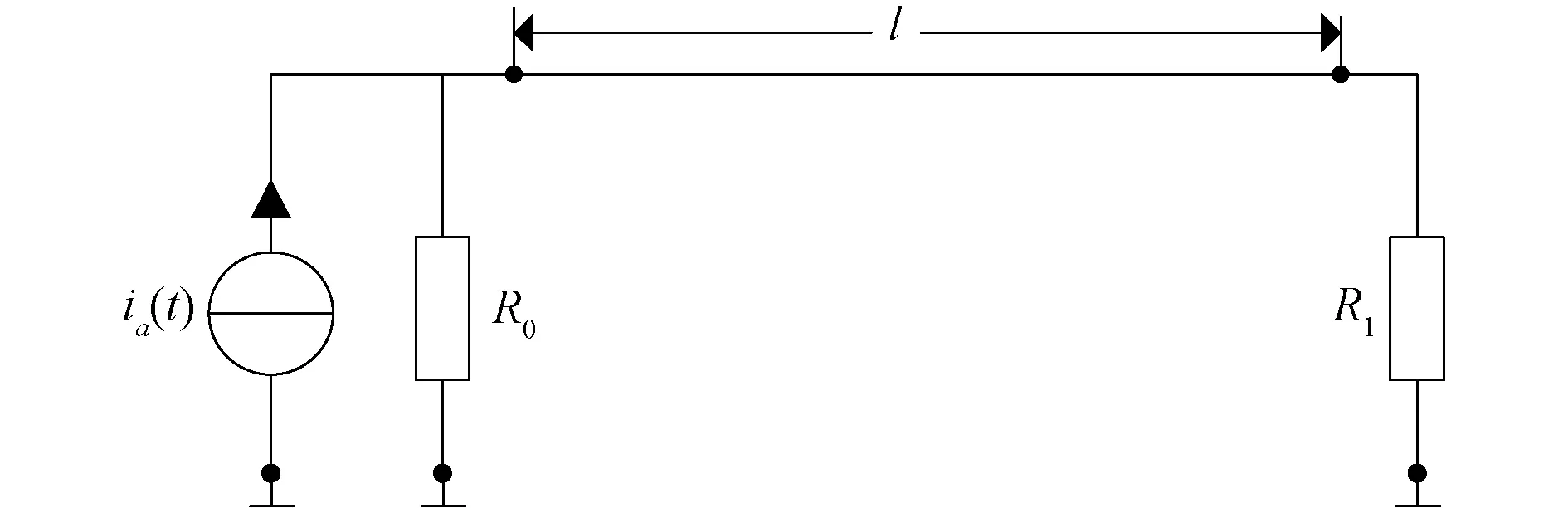
图11 单导体传输线计算电路Fig.11 Geometry of the single conductor transmission line

导线长度取3 120m，对于A-Line方法将导线分别按照每段120m和130m分段进行计算，传输线末端电压分别如图12(a)，(b)所示。

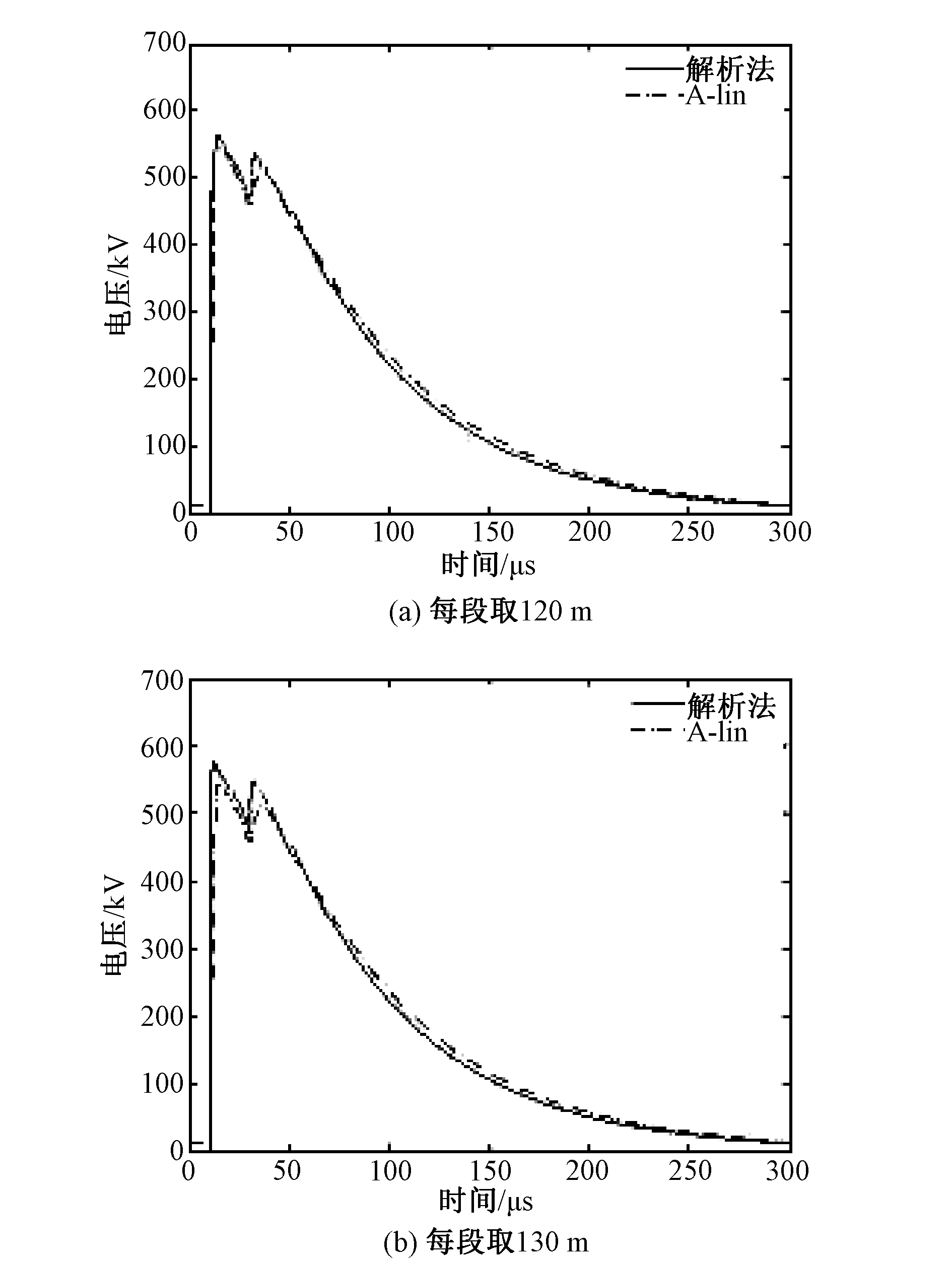
图12 传输线末端电压Fig.12 Voltage at the terminal of transmission line

对于2.6/50μs的雷电流，当导线每段取120m时，最大电压值误差为4.93%，当导线每段取130m时，最大电压误差为5.38%。考虑最大电压误差不超过5%的情况，120m为该算例A-Line模型可取的最大导线长度，验证了本文误差分析的正确性。

3.2 多导体传输线

线路结构如图13所示。空气磁导率μ0=4π×10-7H/m，空气介电常数ε0=8.854×10-12F/m，大地相对磁导率μr=1，大地相对介电常数εr=10，大地电阻率为100Ω·m，导线半径为1.25cm。A相激励为上升时间/半波时间分别为2.6/50μs的双指数雷电流，雷电通道波阻抗取300Ω，线路末端接100Ω电阻。

(1) 导线长度取150m，A、B、C末端电压如图14(a)，(b)，(c)所示。

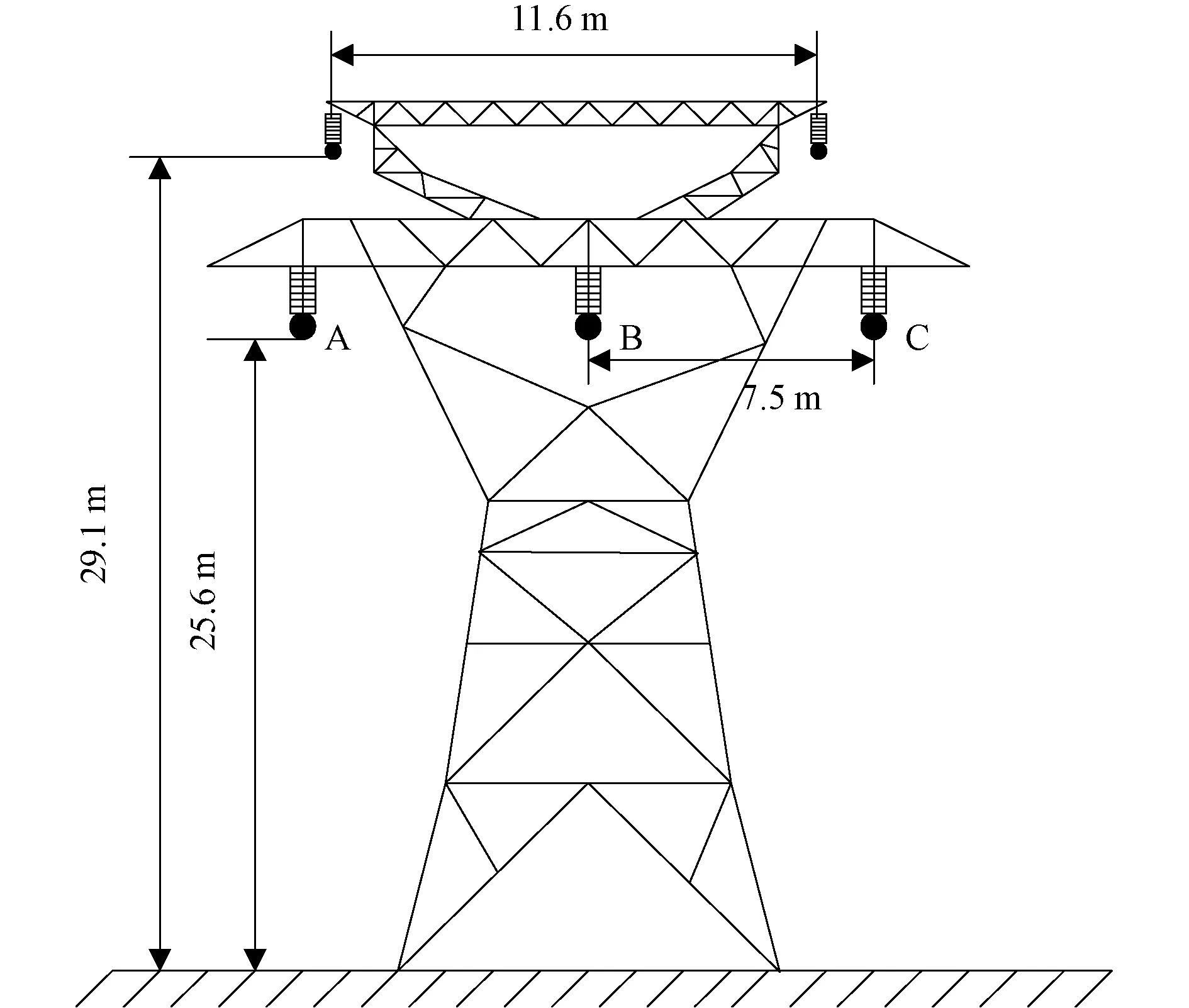
图13 线路结构Fig.13 Geometry of the transmission line

对于以上多导体架空线，导线A、B、C最大电压误差分别为3.33%、3.43%、4.64%。

(2) 将导线长度改为300m，A、B、C末端电压如图15(a)，(b)，(c)所示。

导线A、B、C最大电压误差分别为6.31%、6.56%、8.67%。

(3) 导线长度取300m，将A-line模型分成2段，每段的长度为150m。A、B、C末端电压如图16(a)，(b)，(c)所示。

导线A、B、C最大电压误差分别为3.52%、3.93%、4.67%。

通过以上多导体算例分析可知，考虑最大电压误差不超过5%的情况，150m为该算例A-line模型可取的最大导线长度。当导线长度较长时，可分段进行求解。验证了本文误差分析的准确性。

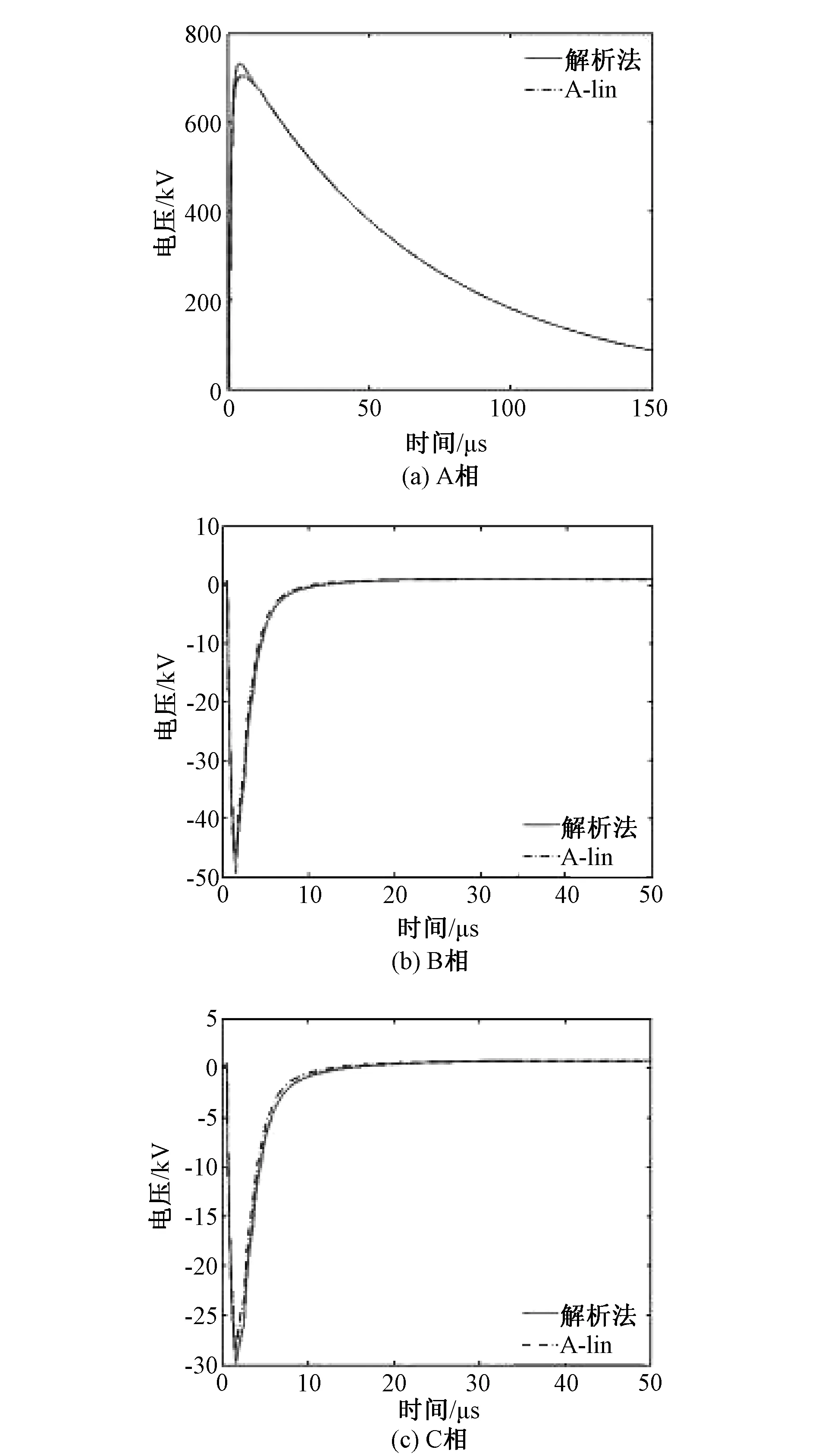
图14 A，B，C末端电压Fig.14 Voltages at the terminal of A, B, C

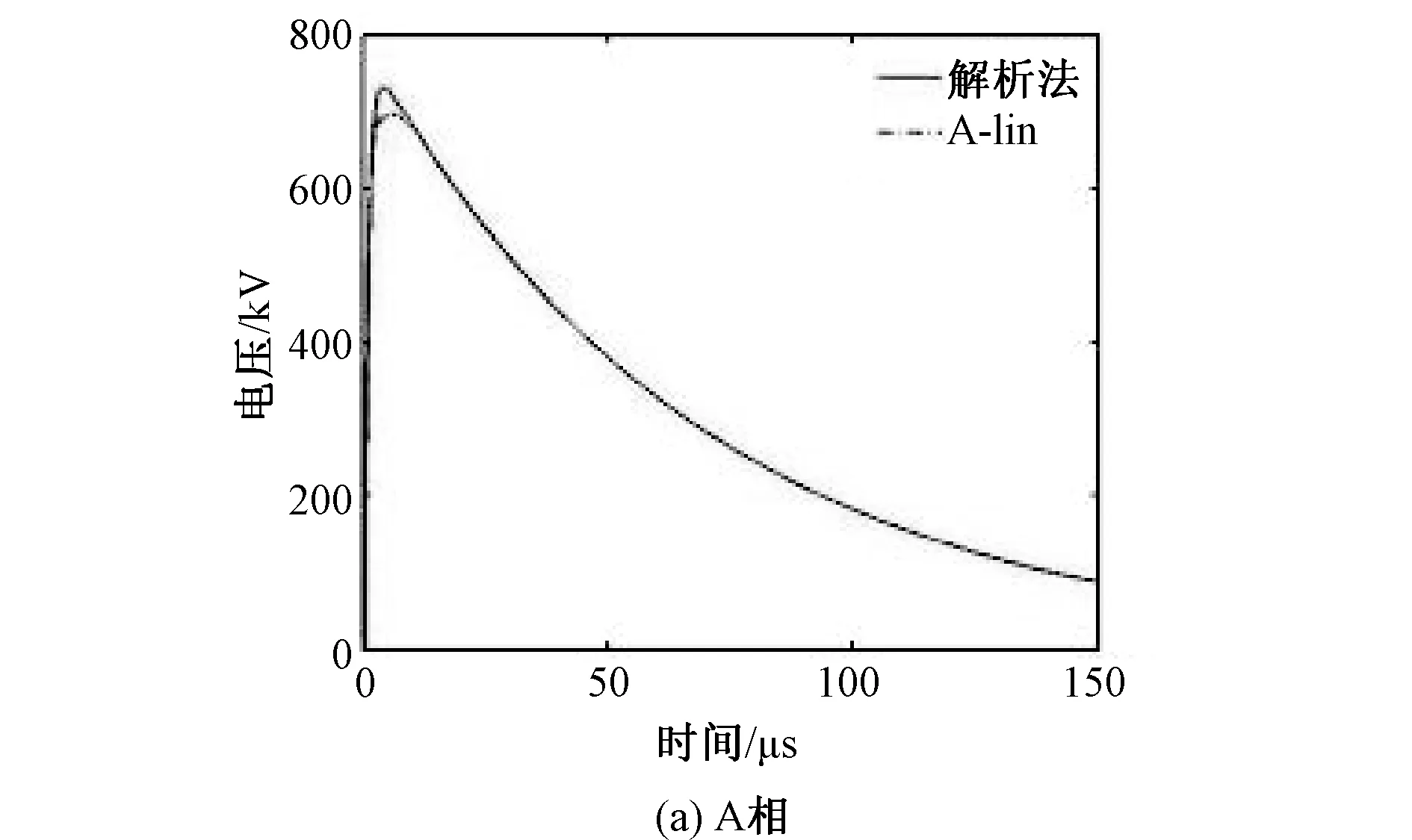
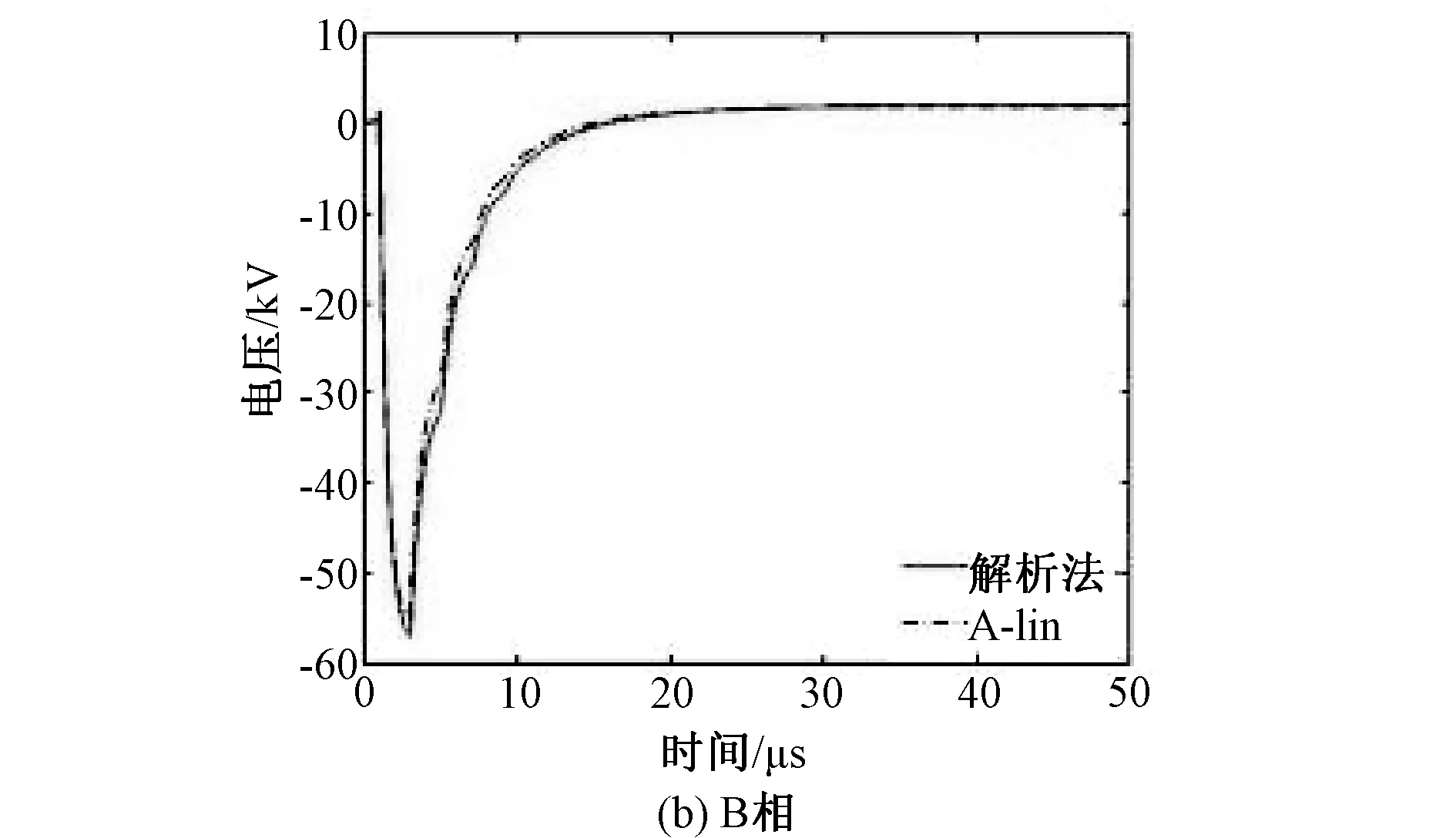
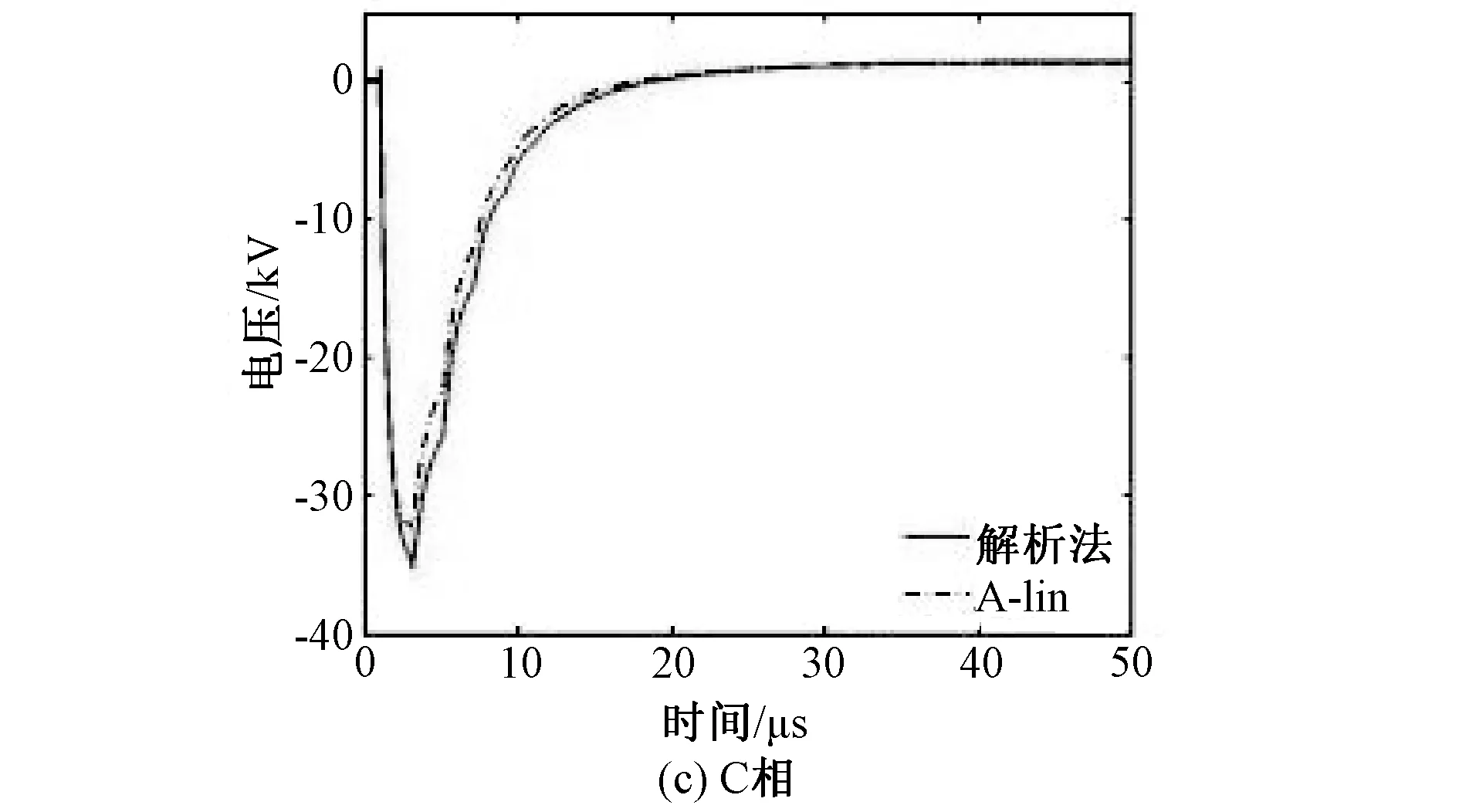
图15 A，B，C末端电压Fig.15 Voltages at the terminal of A, B, C

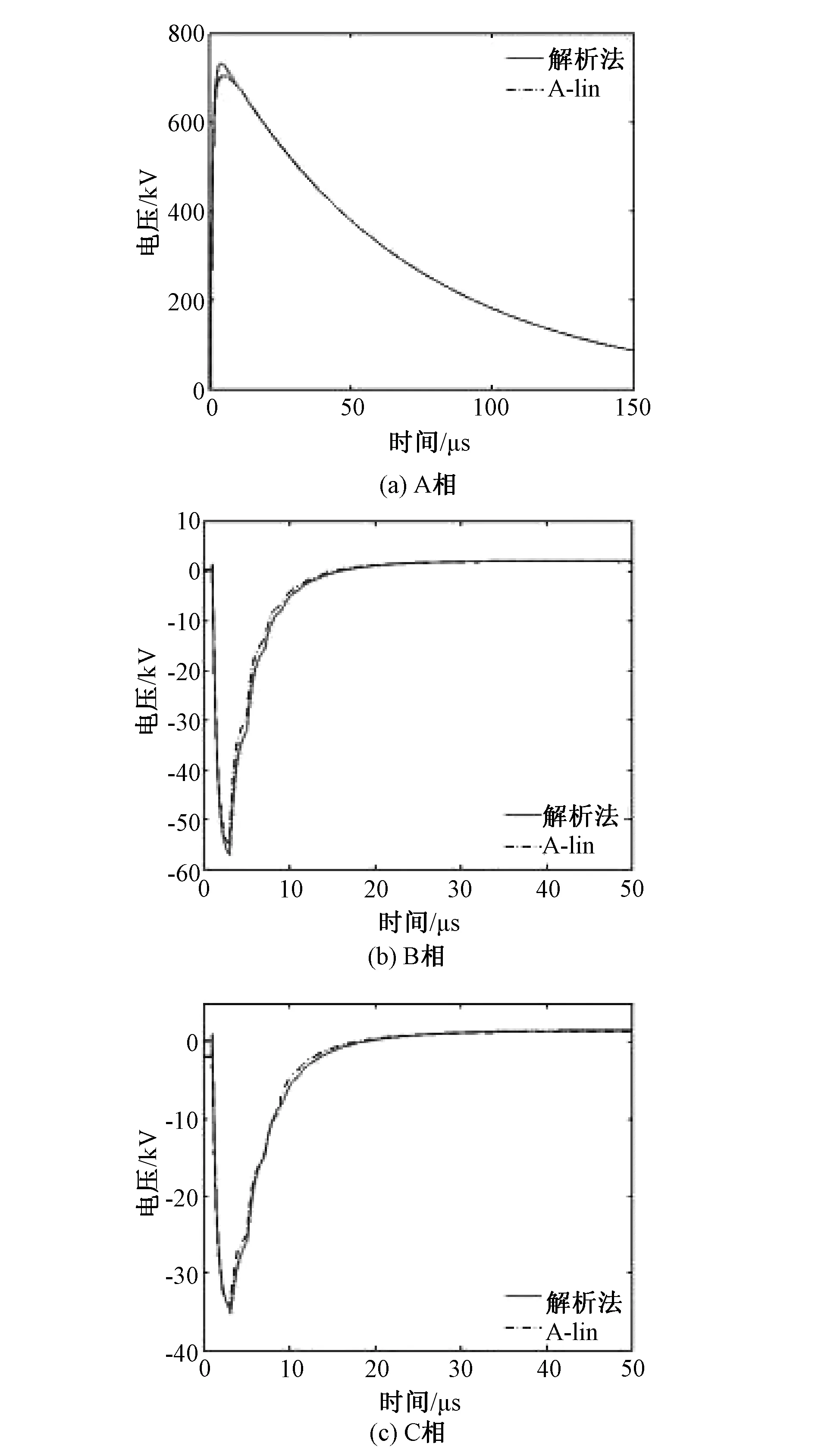
图16 A，B，C末端电压Fig.16 Voltages at the terminal of A, B, C

4 结 论

通过对A-Line模型传输参数矩阵频域误差公式进行推导，得出了该模型的传输线特征阻抗和传播常数误差公式。并进行了误差分析，得出了A-Line模型的适用范围，为该模型的应用提供了理论依据。结合算例分析，验证了本文误差分析的正确性。

通过分析可以看出，A-Line模型的应用受到频率，大地电阻率、导线长度以及导线高度的限制。当频率、大地电阻率，导线长度较大或者导线高度较小时，会产生较大误差。所以对于频率或者大地电阻率较大的情况，导线长度就会限制在较短的范围，而当导线高度较大时范围会有所扩大。在此情况下，对于较长导线的计算，应用A-Line模型时就要进行分段求解。而对于较小频率和大地电阻率的情况，导线长度可以取到较大值。

[1]MARTIJR．Accuratemodelingoffrequency-dependenttransmissionlinesinelectromagnetictransientsimulations[J]．IEEETransactionsonPowerApparatusandSystems，1982，101(1)：147-157．

[2]NAREDOJL，MAHSEREDJIANJ，GUTIERREZ-ROBLESJA，etal．ImprovingnumericalperformanceoftransmissionlinemodelsintheEMTP[C]．IPST2011，Delft，TheNetherlands，June2011．

[3]MORCHEDA，GUSTAVSENB，TARTIBIM．Auniversalmodelforaccuratecalculationofelectromagnetictransientsonoverheadlinesandundergroundcables[J]．IEEETransactionsonPowerDelivery， 1999，14 (3)：1032-1038．

[4]GUSTAVSENB．Avoidingnumericalinstabilitiesintheuniversallinemodelbyatwo-segmentinterpolationscheme[J]．IEEETransactionsonPowerDelivery，2013，28 (3)：1643-1651．

[5]GUSTAVSENB．Passivityenforcementfortransmissionlinemodelsbasedonthemethodofcharacteristics[J]．IEEETransactionsonPowerDelivery，2008，23 (4)：2286-2293．

[6]RAMIREZA，IRAVANIR．EnhancedfittingtoobtainanaccurateDCresponseoftransmissionlinesintheanalysisofelectromagnetictransients[J]．IEEETransactionsonPowerDelivery，2014，29 (6)：2614-2621．

[7]BANUELOSES，GUTIERREZJA，GUSTAVSENB，etal．Enhancingtheaccuracyofrationalfunction-basedmodelsusingoptimization[J]．ElectricPowerSystemsResearch，2015，125：83-90．

[8] 吴维韩，张芳榴．电力系统过电压数值计算[M]．北京：科学出版社，1989．

[9] 徐政．耦合长线电磁暂态分析的扩展Bergeron模型[J]．中国电机工程学报，1996，16(5)：354-357．

[10] 毛军发．高速集成电路中多导体传输线时域响应分析[D]．上海： 上海交通大学，1992．

[11] 李征帆，毛军发．微波与高速电路理论[M]．上海：上海交通大学出版社，2001．

[12] 毛军发，李征帆．多导体传输线时域响应分析的卷积特征法[J]．电子学报，1992，20(9)：47-54．

[13]BRANINFHJr．Transientanalysisoflosslesstransmissionlines[J]．ProceedingsoftheIEEE，1967，55 (11)：2012-2013．

[14] 卢铁兵．变电站瞬态电磁环境数值预测方法的研究[D]．保定：华北电力大学，2002．

[15]NAKHLANM．ACHARR．DEPACT：Delayextraction-basedpassivecompacttransmission-linemacromodelingalgorithm[J]．IEEETransactionsonAdvancedPackaging，2005，28(1)：13-23.

[16] 刘欣，崔翔，齐磊．高速铁路接触网雷电感应过电压计算及其闪络概率研究[J]．华北电力大学学报(自然科学版)，2013，40(2)：10-16．

[17]DOUNAVISA，ACHARR，NAKHLAM．Efficientpassivecircuitmodelsfordistributednetworkswithfrequency-dependentparameters[J]．IEEETransactionsonAdvancedPackaging，2000，23(3)：382-392．

[18]DOUNAVISA，NAKHLAN，ACHARR，etal．Delayextractionandpassivemacromodelingoflossycoupledtransmissionlines[C]．IEEE12thTopicalMeetingElectricalPerformanceofElectronicPackaging,Princeton，NJ，Oct2003：251-254．

[19]PABLOM，JOSEAG，JOSERL，etal．Aeriallinemodelforpowersystemelectromagnetictransientssimulation[J]．IETGeneration,TransmissionandDistribution，2016，10(7)：1597 - 1604．

[20] 杨晓宪，郑涛．多导体传输线分析[M]．北京：中国电力出版社, 2013．

The Error Analysis and Research of A-Line Model Based on Method of Characteristics

LIU Xin，WANG Zhifeng, LIANG Guishu

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

The transmission line model is an important part of electromagnetic transient calculation of power system. Several new models have been proposed in recent years. A new model, called A-Line model, is a double Norton model based on the method of characteristics. In the calculation process of this model, it is not necessary to fit the propagation constant, which makes the calculation of overhead lines transient calculation simpler compared to the J. Marti and ULM models. However, when it deals with time domain convolution of frequency-dependent parameter, port currents of the lines are used instead of the currents along the lines, so there is a certain error for this model and such error relates to the parameters of lines. There are no detailed error analysis and application scope of this model in the existing papers. In this paper, the error formula of characteristic impedance and propagation parameter are deducted and the influence of line parameters on characteristic impedance and propagation constant are studied. So the error of A-Line model and its application scope are analyzed. The result of analysis was verified by some cases, which lays theoretical foundation for engineering application of this model.

transmission line; A-Line model; method of characteristics; convolution calculation; error analysis

10.3969/j.ISSN.1007-2691.2017.03.04

2016-07-28.

国家自然科学基金资助项目(51407073).

TM134

A

1007-2691(2017)03-0022-08

刘 欣(1980-)，男，副教授，主要从事电力系统电磁瞬态计算、电力系统电磁兼容及电力系统过电压数值计算方面的研究；王志峰(1988-)，男，硕士研究生，主要从事电力系统过电压数值计算方面的研究。