三重积分的直角坐标计算方法及其运用研究

余小飞，李 平

(河南工业职业技术学院，河南 南阳 473000)

三重积分的直角坐标计算方法及其运用研究

余小飞，李 平

(河南工业职业技术学院，河南 南阳 473000)

三重积分的计算，应考虑如何将其化为三次积分进行，本文根据积分区域和被积函数的特点，研究几个三重积分的计算。

三重积分；直角坐标；三次积分

0 引言

三重积分在空间物体的质量、引力方面有非常广泛的应用，但三重积分的计算却是非常复杂的，本文将利用直角坐标系来研究三重积分的计算与运用。

1 三重积分的直角坐标计算方法

三重积分的计算是化成三次积分进行的，其实质是计算一个定积分(一重积分)和一个二重积分，然后再将二重积分转化为二次积分。

Σ1:z=z1(x,y)，Σ2:z=z2(x,y)

其中z1(x,y)，z2(x,y)在Dxy上连续，且z1(x,y)≤z2(x,y)。在这种情况下，积分区域Ω可表示为

Ω={(x,y,z)|z1(x,y)≤z≤z2(x,y),(x,y)∈Dxy}

或者

同理，三重积分的计算也可以先对x求定积分，再对y，z求二重积分，有

或者先对y求定积分，再对x，z求二重积分，有

2 应用例析

解将积分区域Ω投影到xOy面上，得投影区域

在Dxy内任取一点(x,y)，过此点作平行于z轴的直线，该直线过平面z=0穿入Ω，过平面z=1-x-y穿出Ω，因此

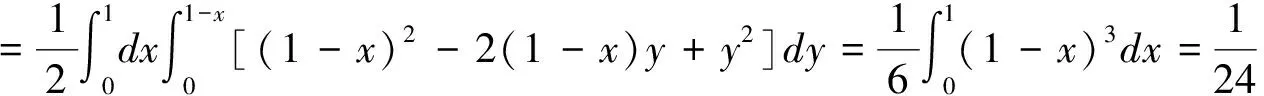
解根据三重积分的性质，可得

又由被积函数的奇偶性和积分区域的对称性，知

而

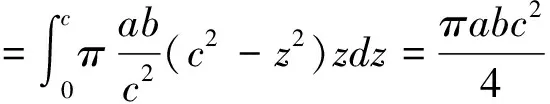
其中积分区域

(0≤z≤c)。

因此

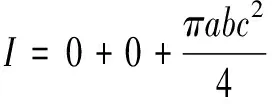
x2+y2=z2，z=1

所界的区域。

解曲面在xOy平面上的射影D为圆盘x2+y2≤1，于是

3 结语

在利用直角坐标计算三重积分时，可化为三次积分来进行，但积分次序的不同，计算过程的复杂程度也不尽相同，在实际计算过程中，应根据积分区域和被积函数的特点，首先运用积分的性质，然后选择恰当的积分次序，可以大大简化计算过程。

[1]费定辉，周学圣.数学分析习题集题解[M].济南：山东科学技术出版社，2008：368-369.

[2]华东师范大学数学系.数学分析[M].第三版下册.北京:高等教育出版社，2006：247-251.

(编辑 赵欣宇)

Research on the Calculation Method and Application of Rectangular Coordinates of Three Integral

YU Xiaofei, LI Ping

(Henan Polytechnic Institute, Nanyang 473000, China)

Calculation of the three integral, should consider how to convert it into the triple integral. In this paper, the calculation of several integrals of the three integral according to the characteristics of the integral region and the integrand.

three integral; rectangular coordinates; the triple integral

2017-03-14

余小飞(1986-)，理学硕士，讲师。主要研究方向：基础数学。

G712

A

1672-0601(2017)05-0085-02