应力历史影响下的膨胀土动力参数响应特征

李晶晶， 孔令伟

(1.中国科学院 武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2. 中国科学院大学，北京 100049)

应力历史影响下的膨胀土动力参数响应特征

李晶晶1,2， 孔令伟1,2

(1.中国科学院 武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2. 中国科学院大学，北京 100049)

动剪切模量和阻尼比是土动力非线性性能中最重要的两个参数。为考虑应力历史对膨胀土动力学特性的影响，开展加载、卸载和再加载固结路径下南阳膨胀土共振柱试验，利用双曲线模型和经验关系分别对动剪切模量和阻尼比随剪应变演化规律进行分析，提出膨胀土在剪应变值为5×10-6～10-2范围内的剪切模量比和阻尼比推荐值，同时分析应力历史影响下动剪切模量比和阻尼比的不确定性。研究表明，应力历史对最大动剪切模量与动剪切模量随剪应变演化规律都有很大影响，卸载和再加载条件下的最大动剪切模量较加载条件下的大，最大增幅为66.59%；应力历史对阻尼比的影响规律性不强。动剪切模量比的极小值均出现在加载路径；经历较大外荷载后，卸载程度越大，动剪切模量比不确定性越大；动剪切模量比和阻尼比的变异系数最大值分别达到了46.30%和48.99%，说明在工程设计和施工中应充分考虑应力历史对动剪切模量比和阻尼比的影响，根据相应的应力历史来选取土体动力学参数。

膨胀土；共振柱；动剪切模量；阻尼比；应力历史

膨胀土是一种被视为“工程界癌症”的特殊性高塑限黏土，广泛分布于我国20多个省市。随着我国高速铁路的发展、重载铁路的改造和高速公路的修建，均将穿越大量的膨胀土地段。在此类工程场地地震安全性评价、沉降预测[1]以及高速铁路、重载铁路等震动反应分析中，动剪切模量和阻尼比是最重要的两个参数，其选取的合理性将直接影响着工程安全和工程造价，因此，对其进行研究具有重要的工程意义。

目前，土体动力特性研究的对象涉及到各种土体，研究地域从陆地[2-7]延伸到了海洋[8]，甚至是月球(月壤)[9]，许多学者给出了相应剪应变下土体的动剪切模量比和阻尼比的推荐值，为类似工程场地的设计、施工中的沉降变形分析及抗震分析等提供参考依据。然而，大部分的研究仅考虑了应力水平对动剪切模量和阻尼比的影响。在自然界中，土的形成过程十分复杂，其对应力历史有一定的记忆性；再者，人工堑坡、路基等需要填方或是挖方，必要时还将对土体进行换填，土体在不同的施工过程中所经历的应力路径是存在差别的，比如，填方路基的原位土体经历了加载路径；挖方路基的原位土体经历了卸载路径；而路基土体为膨胀土时，浅层膨胀土可能需要挖除换填，因此下层土体经历了卸载-再加载的应力路径。因此，土的应力不应只考虑作为一般固体力学应力理论中的应力状态，还应考虑其特有的应力历史、应力路径和应力水平[10]。

岩土体具有复杂的变异性和参数的不确定性，土性指标的不确定性对结果的影响远远超过计算方法的不确定性的影响，动剪切模量比和阻尼比这两个土体动力参数对地面运动影响显著，如在三类场地加速度为0.1g地震输入时，6%的动剪切模量比误差对反映谱的影响已经不能忽视[11]，而同样应力水平，不同应力历史影响下土体的动剪切模量比和阻尼比的不确定性研究鲜见报道。

综上，本文依托内(乡)-邓(州)高速公路边坡工程背景，选取南阳典型膨胀土原状样，基于共振柱试验，研究不同应力路径下膨胀土小应变动力特性响应特征，以期得到动剪切模量和阻尼比随剪应变发展的演化规律，同时简单分析应力历史影响下，南阳膨胀土动剪切模量比和阻尼比的变异性。

1 土样性质与试验方法

1.1 土样性质

试验土样取自于河南南阳某堑坡典型膨胀土地层，利用探坑法获取试样，取样深度为4 m，土样为红褐色，呈硬塑-坚硬状，含黑色铁锰结核和黄白色姜石。

根据《公路土工试验规程》对试验土样进行物性指标试验及XRD衍射试验，其基本物理性质指标和矿物成分，如表1，表2所示。从颗粒分析试验结果可知，南阳膨胀土黏粒含量(小于0.005 mm)占44.8%，其中，小于0.001 mm的颗粒占27%，而土样的自由膨胀率主要由土样中小于0.001 mm粒径的颗粒含量所决定[12]，因此，南阳膨胀土具有较高的塑性(IP=29.2%)和膨胀性(δef=62%)。同时，南阳膨胀土的黏土矿物含量高达52%，且以强亲水性矿物蒙脱石和绿泥石为主，分别占黏土矿物总量的30%和35%。

表1 南阳膨胀土的物理性质指标Tab.1 Physical property indexes of Nanyang expansive soil

表2 南阳膨胀土的矿物成分Tab.2 Mineral compositions of Nanyang expansive soil

为了了解该膨胀土经历的应力历史，由膨胀土原状样的室内压缩曲线(见图1)，通过Cassagrande方法确定其先期固结压力pc为160 kPa，而当前上覆土层压力约80 kPa，该膨胀土具有一定的超固结性。

1.2 试验方法

试验仪器采用英国GDS公司生产的固定-自由型Stokoe共振柱(Resonant Column Apparatus，RCA)，是目前国际上最常用的共振柱试验仪之一，其试验精度达10-10。

原状土试样尺寸为直径Ø=50 mm、高H=100 mm的实心圆柱土样，试验在(23±1) ℃环境下进行，试验步骤为：

图1 膨胀土压缩曲线Fig.1 Compression curve of expansive soil

步骤1 固结：试样采用等压固结方式，固结压力如表3所示，为了研究先期固结压力和当前固结压力对膨胀土小应变刚度特性的影响，设置的最大固结压力(320 kPa)大于先期固结压力160 kPa，最小固结压力为零，小于当前固结压力80 kPa。同时，考虑应力历史的影响，固结应力路径分为加载路径、卸载路径和再加载路径。

步骤2 共振柱激振：固结完成后，对试样进行共振柱激振试验，激振电压经试验，从0.001 V开始，逐级增加，记录各个激振电压下土体的共振频率、动剪应变、阻尼比等，直到剪应变值接近10-4，方便起见，称激振时的固结压力为激振围压σ3。

步骤3 数据处理：根据共振频率、试样密度和尺寸等，计算试验的动剪切模量Gd(式(1))和阻尼比λ(式(2))[13]。

(1)

(2)

式中：fn为共振时的频率；hc为试样固结后的高度；βs为扭转激振式的无量纲频率因素；AN和AN+m分别为第N和N+m次的振幅。

表3 试验方案Tab. 3 Schemes of the test

2 试验结果分析与讨论

2.1 南阳膨胀土动力学参数预测模型选取

对动剪切模量Gd-剪应变γ关系描述，具有代表性的模型包括Maitin-Davidenkov方程(式(3))、Stokoe方程(式(4))和Hardin-Drnevich方程(式(5))，最大动剪切模量Gmax一般由模型拟合得到。

(3)

式中：A、B、γ0均为与土性有关的拟合参数。

(4)

式中：α为曲率系数，γr表示Gd/Gmax=0.5时对应的参考剪应变。

(5)

式中：γr为参考剪应变。

由3个典型方程得到的不同应力路径和激振围压下的最大动剪切模量Gmax，如表4所示。由表4可知，不同方程得到相同条件下的Gmax相差不大，以Stokoe方程和Maitin-Davidenkov方程拟合得到的Gmax与Hardin-Drnevich方程得到的Gmax分别相差-2.07%～0.82%和-2.76%～0.40%。然而，3个方程得到的Gd-γ衰减曲线形态却存在差异(图2)，剪应变小于0.05%时，3个方程拟合曲线近乎重合，但随着剪应变的增加，Maitin-Davidenkov方程拟合曲线逐渐偏离另两条拟合曲线，这是由于Maitin-Davidenkov方程含有较多的拟合参数(4个)，能更准确的拟合试验点，然而，方程的拟合参数越多，意味着其不确定性越大，试验获得的数据在剪应变小于0.05%范围内，因而，在剪应变大于0.05%时，其拟合曲线或向上(图2(a)、图2(b))或向下(图2(c))偏离另外两条拟合曲线。所以，能否用Maitin-Davidenkov方程预测南阳膨胀土试验范围外的剪应变(>0.05%)土体的刚度衰减规律还有待进一步考证。

表4 不同方程下的最大动剪切模量GmaxTab.4 Gmax of different equations

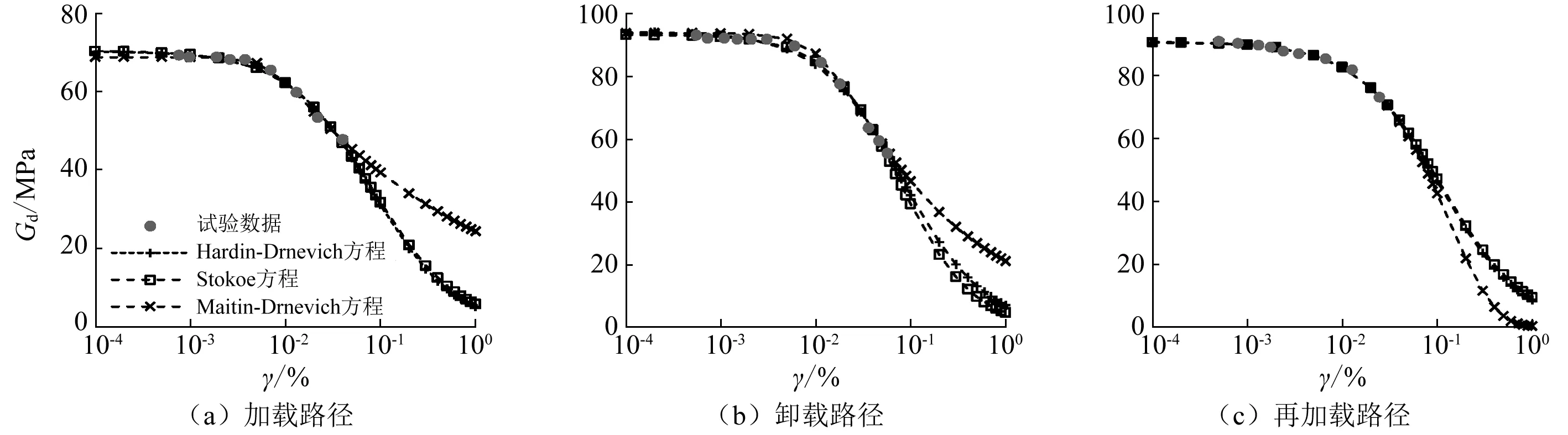
图2 激振围压为80 kPa时不同方程和应力路径下的Gd-γ衰减曲线Fig.2 Relationship between Gd and γ of different equations and stress paths under 80 kPa excitation confining pressure

经上述分析，简单的Hardin-Drnevich方程就能较好地描述南阳膨胀土刚度衰减特性，因此，下面以Hardin-Drnevich方程对动剪切模量及其衰减规律进行分析。

土体动力学参数除了动剪切模量外，阻尼比也是一个重要参数。经分析，用经验公式(6)能较好地描述南阳膨胀土阻尼比随剪应变变化规律。

λ=λmax(1-Gd/Gmax)n

(6)

式中：λmax为γ趋于无穷大时的阻尼比；n为拟合参数。

2.2 应力历史对南阳膨胀土Gmax影响规律

由表4整理得到不同应力历史下南阳膨胀土最大动剪切模量与激振围压关系曲线，如图3所示。从图3可知，膨胀土的Gmax与σ3、应力历史相关，应力历史相同时，Gmax随着σ3的增加而增大；相同σ3下，卸载段和再加载段的Gmax明显比加载段的Gmax大，σ3值比最大固结压力(这里为320 kPa)小的越多，加载路径和卸载(或再加载)路径下的Gmax差值就越大，如σ3为0和160 kPa时，卸载(或再加载)的Gmax比加载的Gmax分别大了66.59%和13.37%。这是由于土体具有压硬性，土体在外载荷的作用下，逐渐被压密，如外载荷从80 kPa增加到320 kPa，其孔隙比由图4中的A1点减小到D点，随后又经历卸载和再加载过程，相当于图4中的D-B2-A2段和A3-B3段，由此可知，加载段的孔隙比比卸载(或再加载)段大得多，这里表现在加载段具有较小的动剪切模量；而卸载段的孔隙比比再加载段的孔隙比稍大，但相差甚微，其动剪切模量也相差不大。

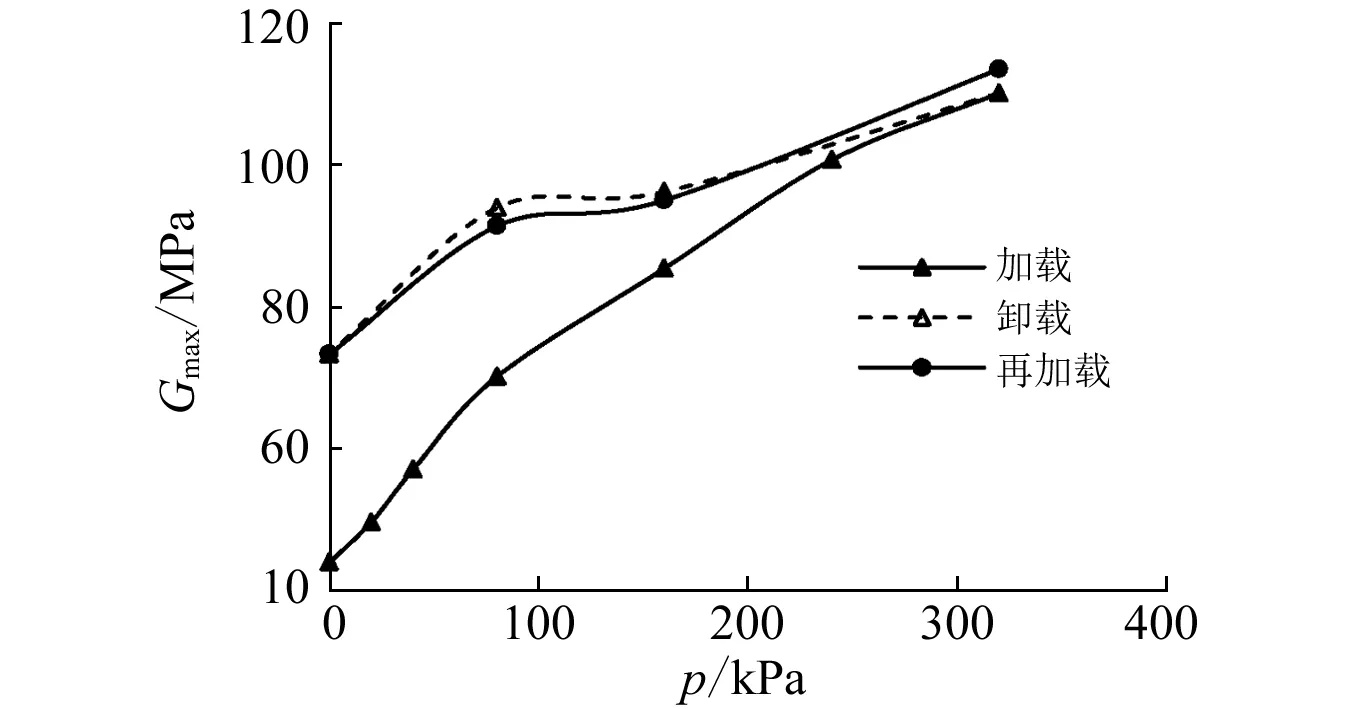
图3 最大动剪切模量Gmax与激振围压σ3关系曲线Fig.3 Relationship between Gmax and σ3

图4 固结压缩回弹曲线Fig.4 Relationship between e-lgP from compression test

从图3还可知，相同应力历史的Gmax-σ3曲线都在σ3为80 kPa附近出现了拐点，卸载段和再加载段分段式更加明显；与此同时，在卸载段和再加载段，σ3在80 kPa和160 kPa之间，Gmax出现了较平缓段，这说明膨胀土的当前上覆压力和先期固结压力对其Gmax都有一定的影响作用。

2.3 应力历史影响下南阳膨胀土Gd、λ演化规律

由上述分析可知，激振围压和应力历史对Gmax有很大的影响作用，它们对膨胀土刚度衰减特性同样有显著影响，图5、图6分别给出了不同激振围压和不同应力历史下，膨胀土动剪切模量(阻尼比)随剪应变发展规律曲线。

从图5可知，应力历史相同时，σ3越大，Gd-γ衰减曲线越偏离γ轴；当γ较小时，不同σ3下Gd衰减速率相近，但随着γ的发展，σ3越大，Gd衰减越快。对比图5(a)和图5(b)，发现卸载路径下，不同σ3间的Gd-γ衰减曲线间相距更紧密，说明膨胀土经历较高的外载荷后卸载，其刚度并没有按比例减小，而在很大程度上得到了保留。从图6能更直观地看出，相同γ条件下，卸载(或再加载)路径下膨胀土的Gd比加载路径下的Gd大，且γ小于0.01%时，3种应力路径下Gd的衰减速率近乎相同。

对比图6(a)和图6(b)，可以看出不同应力历史下，σ3为160 kPa的Gd-γ衰减曲线簇较σ3为80 kPa的Gd-γ衰减曲线簇相距更紧密，说明动剪切模量衰减规律与最大动剪切模量规律相似，σ3值比最大固结压力小的越多，剪应变相同时，不同应力历史下的Gd差值也越大。

与Gd随γ演化规律相比，λ的数据较为离散，λ-γ拟合效果稍差，其与σ3和应力历史的关系并未存在着明显的规律性；λmax也不存在文献[3]中提到的与围压呈负相关性，这可能是λ受土体性质的影响。但从图6可知，随着γ的增加，λ总体上呈现增长的趋势。

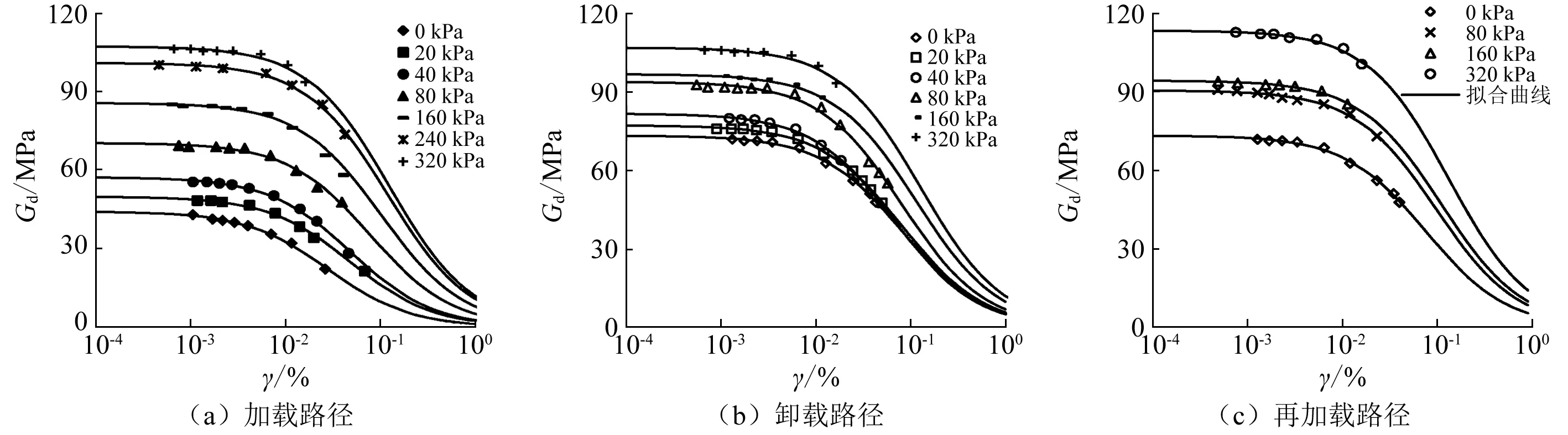
图5 不同激振围压下的Gd-γ衰减曲线Fig.5 Relationship between Gd and γ under different excitation confining pressures

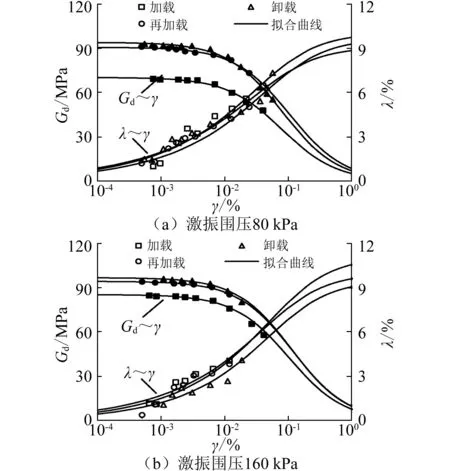
图6 不同应力路径下的Gd、λ与γ关系曲线Fig.6 Relationship between Gd, λ and γ under different stress paths

2.4 南阳膨胀土Gd/Gmax和λ的推荐值

Gd/Gmax和λ是土动力非线性性能中最重要的两个参数，图6、图7给出了λ、Gd/Gmax和λ/λmax随γ变化关系曲线。相同激振围压，不同应力历史下，土体动剪切模量的归一化效果较阻尼比的归一化效果好。目前工程上使用的数值化结果是以γ在5×10-6、1×10-5、5×10-5、1×10-4、5×10-4、1×10-3、5×10-3和1×10-2这8个典型值给出的结果，为了给膨胀土工程设计和施工提供数据支持和参考依据，本文也给出这8个典型应变下，膨胀土的Gd/Gmax、λ的参考值，如表5、表6所示。由于这两个土动力学参数具有明显的不确定性，表中也给出了不同应力历史影响下，其参考值的不确定性统计结果。

与以往研究给出的黏土的Gd/Gmax和λ值相比，南阳膨胀土的Gd/Gmax值在其范围内，而λ值的极小值稍小于以往研究。说明本文得到的结果较为可靠，同时，本文给出的范围更细化(包含不同围压和应力历史)，可以为不同深度和经历不同应力路径的膨胀土路基、堑坡工程设计提供参考。

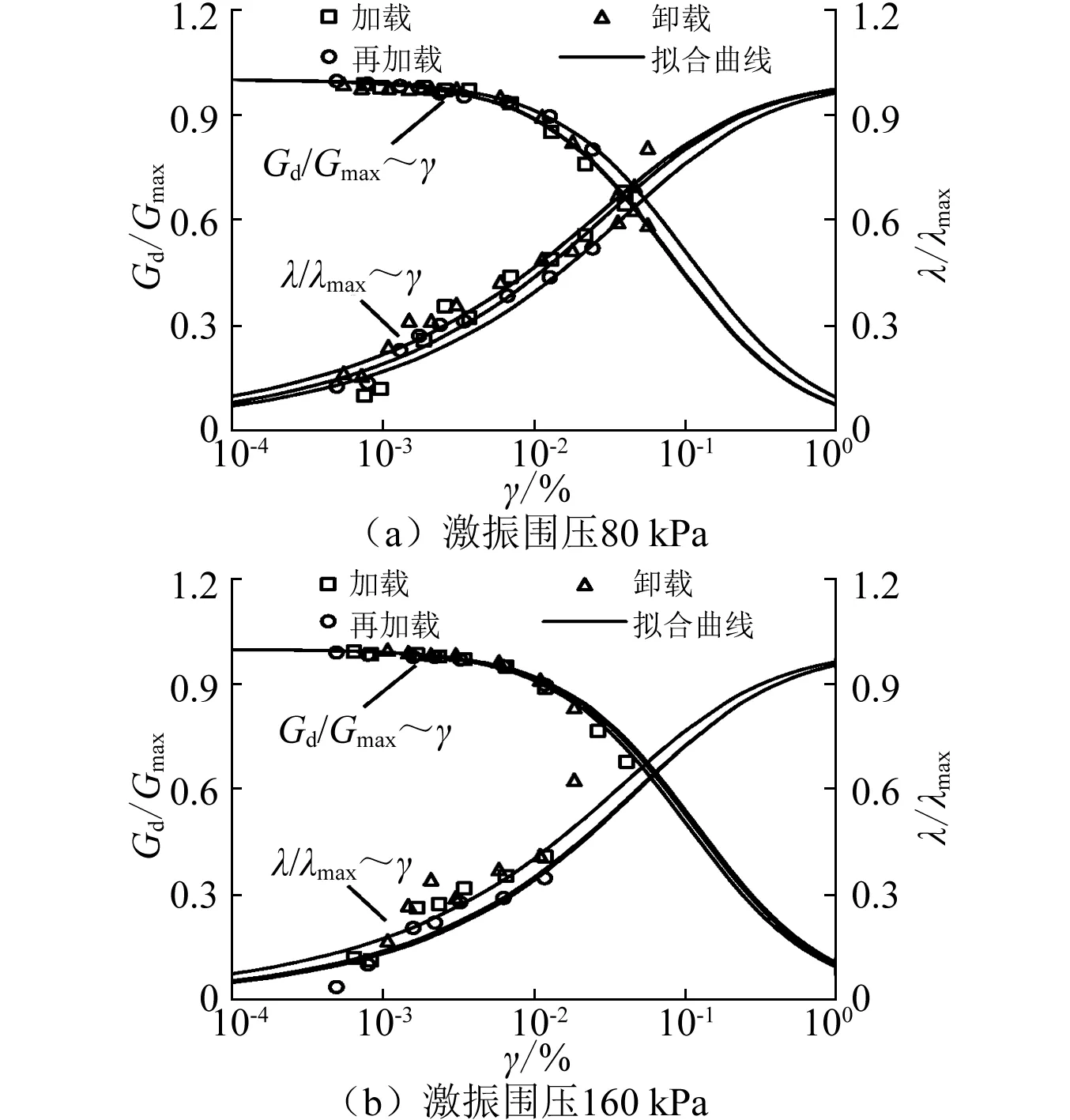
图7 膨胀土Gd/Gmax、λ/λmax与γ关系曲线Fig.7 Relationship between Gd/Gmax, λ/λmax and γ

经数据整理可以发现，Gd/Gmax与应力历史呈现一定的规律性，加载土体的Gd/Gmax一般是三者中最小的，说明一般情况下，Gd/Gmax越小，膨胀土动剪切模量衰减越慢。剪应变在10-4～10-3区间内是土层地震反应计算中动剪切模量比最常出现的剪应变范围，从表5可知，在此剪应变区间内，膨胀土Gd/Gmax的变异系数在0.41%～33.89%之间，且激振围压越小，其变异系数越大；同时，各激振围压下其标准差最大值均出现在剪应变为5×10-4或1×10-3。此外，只有激振围压为160 kPa和320 kPa时，在8个典型应变下相应的变异系数均小于6%；激振围压越小，剪应变值越大时，变异系数也越大。这说明应力历史对膨胀土Gd/Gmax影响显著，在实际工程设计和施工中要充分考虑应力历史的作用，根据土体实际的应力历史(或应力路径)选取对应的动剪切模量及其比值。

相比而言，λ与应力历史关系的规律性就没那么明显(表6)，其极大值或极小值可能出现于不同的应力历史；但从其变异系数的数值上来看，应力历史对λ的影响也是相当显著的，其变异系数最大值达到了44.99%。

表5 南阳膨胀土Gd/Gmax参考值及其不确定性统计结果Tab. 5 Reference values of Gd/Gmax and its uncertainty for expansive soil in Nanyang

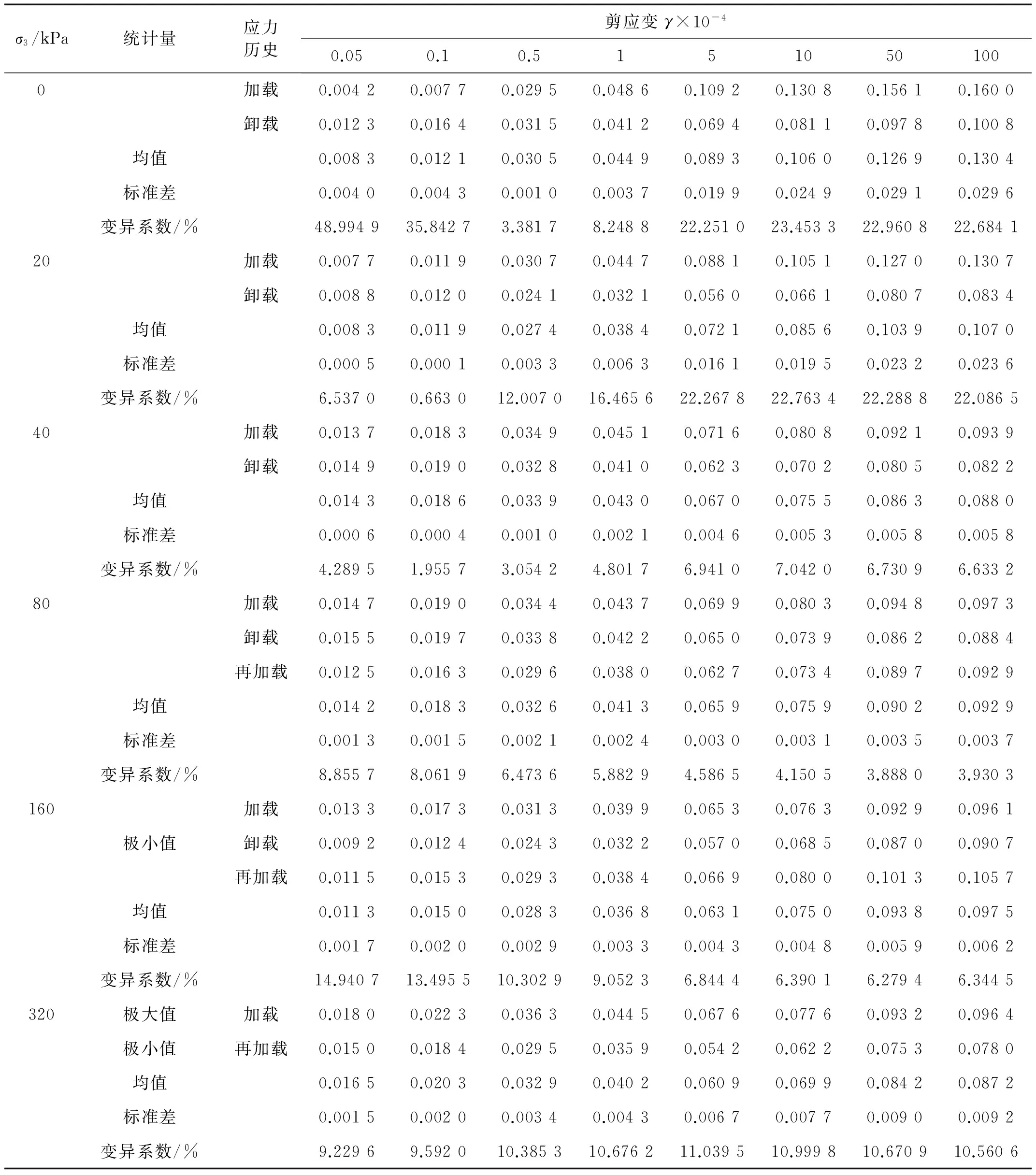
表6 南阳膨胀土λ参考值及其不确定性统计结果Tab.6 Reference values of λ and its uncertainty for expansive soil in Nanyang

3 结 论

(1)应力历史对最大动剪切模量与动剪切模量随剪应变演化规律都有很大影响，卸载和再加载条件下的动剪切模量较加载条件下的大，最大增幅为66.59%；但应力历史与阻尼比相互关系不显著。

(2)最大动剪切模量与围压关系曲线出现拐点，这可能是膨胀土的先期固结压力和当前上覆压力对膨胀土最大动剪切模量具有一定程度的影响作用。

(3)动剪切模量比的极小值均出现在加载路径；经历较大外荷载后，卸载程度越大，动剪切模量比不确定性越大；动剪切模量比和阻尼比的变异系数最大值分别达到了46.30%和48.99%，说明在工程设计和施工中要充分考虑应力历史对动剪切模量比和阻尼比的影响，根据土体实际经历的应力路径选取与之对应的动力参数。

(4)本文得到8个典型剪应变下膨胀土的动剪切模量比和阻尼比的参考值，在以往研究的黏土相应值范围内，说明试验结果具有可靠性；与此同时，本文给出了不同围压和应力历史下的参考值，可以为类似场地不同深度和应力历史的工程设计提供参考依据。

[1] FAHEY M, LEHANE B M, STEWART D. Soil stiffness for shallow foundation design in the Perth CBD[J]. Australian Geomechanics Journal, 2003, 38(3): 61-90.

[2] 孙田, 陈国兴, 王炳辉, 等. 砾石颗粒形状对砂砾土动剪切模量和阻尼比影响的试验研究[J]. 岩石力学与工程学报, 2014, 33(增刊2): 4211-4217. SUN Tian, CHEN Guoxing, WANG Binghui, et al. Experimental research of effect of granule shape on shear modulus and damping ratio of gravel[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup2): 4211-4217.

[3] 蔡辉腾, 李英民, 欧秉松. 福州地区典型土动剪切模量与阻尼比的试验研究[J]. 岩土力学, 2010, 31(2): 361-365. CAI Huiteng, LI Yingmin, OU Bingsong. Testing study of dynamic shear modulus and damping ratio of typical soils in Fuzhou area[J]. Rock and Soil Mechanics, 2010, 31(2): 361-365.

[4] 袁晓铭, 孙锐, 孙静, 等. 常规土类动剪切模量与阻尼比的试验研究[J]. 地震工程与工程振动, 2000, 20(4): 133-139. YUAN Xiaoming, SUN Rui, SUN Jing, et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4): 133-139.

[5] 陈国兴, 刘雪珠, 朱定华, 等. 南京新近沉积土动剪切模量比与阻尼比的试验研究[J]. 岩土工程学报, 2006, 28(8): 1023-1027. CHEN Guoxing, LIU Xuezhu, ZHU Dinghua, et al. Experimental studies on dynamic shear modulus ratio and damping ratio of recently deposited soils in Nanjing[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 1023-1027.

[6] 王志杰, 骆亚生, 王瑞瑞, 等. 不同地区原状黄土动剪切模量与阻尼比试验研究[J]. 岩土工程学报, 2010, 32(9): 1464-1469. WANG Zhijie, LUO Yasheng, WANG Ruirui, et al. Experimental study on dynamic shear modulus and damping ratio of undisturbed loess in different regions[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1464-1469.

[7] 杨果林, 邱明明, 何旭, 等. 膨胀土路堑基床新型防水层振动荷载下服役性能试验研究[J]. 振动与冲击, 2016, 35(5): 2-7. YANG Guolin, QIU Mingming, HE Xu, et al. Tests for working property of water-proof layer of cutting subgrade in expansive soil under vibrating load [J]. Journal of Vibration and Shock, 2016, 35(5):2-7.

[8] 尹松, 张先伟, 孔令伟, 等. 海洋沉积土动剪切模量与阻尼比的试验研究[J]. 岩土力学, 2015, 36(增刊1): 459-464. YIN Song, ZHANG Xianwei, KONG Lingwei, et al. Testing study of dynamic shear modulus and damping ratio of seabed sediment[J]. Rock and Soil Mechanics, 2015, 36(Sup1): 459-464.

[9] 张宇, 余飞, 陈善雄, 等. CAS-1模拟月壤动剪切模量与阻尼比的试验研究[J]. 岩土力学, 2014, 35(1): 74-82. ZHANG Yu, YU Fei, CHEN Shanxiong, et al. Experimental study of dynamic shear modulus and damping ratio of CAS-1 lunar soil simulant[J]. Rock and Soil Mechanics, 2014, 35(1): 74-82.

[10] 谢定义, 姚仰平, 党发宁. 高等土力学[M]. 北京: 科学出版社, 2008.

[11] 孙锐, 陈红娟, 袁晓铭. 土的非线性动剪切模量比与阻尼比不确定性分析[J]. 岩土工程学报, 2010, 32(8): 1228-1235. SUN Rui, CHEN Hongjuan, YUAN Xiaoming. Uncertainty of non-linear dynamic shear modular ratio and damping ratio of soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(8): 1228-1235.

[12] 谭罗荣, 孔令伟. 特殊岩土工程土质学[M]. 北京: 科学出版社, 2006.

[13] 谢定义, 陈存礼, 胡再强. 试验土工学[M]. 北京: 高等教育出版社, 2011.

The influence of stress history on the dynamic parameters of expansive soils

LI Jingjing1,2, KONG Lingwei1,2

(1. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

Dynamic shear modulus and damping ratio are the most important parameters for nonlinearity characteristics of the soil dynamic property. To consider the influence of stress history on the dynamic characteristics of expansive soils, resonant column tests were carried out with compression paths of loading, unloading and reloading. Hyperbola models and empirical relationship were used to analyze the dynamic shear modulus and damping ratio, respectively. The recommended values of dynamic shear modulus ratio and damping ratio with shear strain of 5×10-6- 10-2were proposed, and their uncertainty affected by stress history was analyzed. Results show that stress history has a pronounced influence on the maximum of dynamic shear modulus and its decay rule. The dynamic shear modulus is greater in unloading and reloading path than that of loading path, the greatest amplification of which is 66.59%, but it seems that there is no obvious connection between stress history and damping ratio. After experiencing higher load, the more unloading extent is, the greater uncertainty of dynamic shear modulus ratio is. The maximum variation coefficients of dynamic shear modulus ratio and damping ratio are up to 46.30% and 48.99%, respectively. Conclusion can be drawn that the influence of stress history on dynamic shear modulus ratio and damping ratio should be taken into account in engineering design and construction. Dynamic parameters should be selected on the basis of corresponding stress history of the soil.

expansive soil; resonant column test; dynamic shear modulus; damping ratio; stress history

国家自然科学基金重点项目(41430634)

2016-08-08 修改稿收到日期： 2016-10-25

李晶晶 女，博士生，1989年生

孔令伟 男，博士，研究员，博士生导师，1967年生

E-mail:lwkong@whrsm.ac.cn

TU41;TU443

A

10.13465/j.cnki.jvs.2017.12.030