基于BSM模型的房地产奇异期权研究

舒家先 吴航宇 金子杰

(安徽财经大学 金融学院，安徽 蚌埠 233030)



基于BSM模型的房地产奇异期权研究

舒家先 吴航宇 金子杰

(安徽财经大学 金融学院，安徽 蚌埠 233030)

本文以期权的思维来重新看待中国的高房价难题，结合当前房地产市场的实际情况，在传统BSM期权定价模型的基础上对其进行改良，设计出一款以锁定特定期限购房权利、以期权到期日房产价格为执行价格的奇异期权，来缓解由投机需求导致的高房价问题。

房地产；BSM期权定价模型；奇异期权定价

期权是人类在金融领域中最伟大的发明之一，所谓期权是指赋予其购买者在规定期限内按双方约定的执行价格，出售或购买一定数量的某种标的资产的权利。期权的买卖双方分别履行权利与义务，这种特性使得期权成了一种有效的风险控制工具，1973年芝加哥期权交易所的正式成立标志着期权时代的开始。传统的对期权定价的方法主要有BSM期权定价模型、[1-2]Cox二叉树期权定价模型、[3-4]模特卡罗模拟，[5]以及风险中性定价方法等，[6]随着金融期权理论的快速发展，在金融期权理论基础上发展起来的实物期权也在学术与实务界得到了广泛的应用与研究。[7]实物期权是在期权发展过程中逐步衍生出来的，是不同于一般股票期权的奇异期权。其底层证券是既非股票又非期货的实物商品，目的是让实物的管理者能够对所拥有实物资产进行有效地管理与投资，使得实物拥有者具有更多的投资可能性。[8]在实物期权中，房地产期权的相关研究还比较少，不管是在学术领域还是实务领域，很少有人涉足于此，一个原因在于期权本身就具有高度的复杂性，在国内市场股指期权、股票期权等传统期权都屈指可数的情况下，实物期权尤其是房地产期权的研究就鲜有人问津。另一个原因是我国传统的购房观念，由于我国当前家庭的金融资产结构存在较大的扭曲，大量的资金都沉淀在房地产这样一个大蓄水池中。[9]一般家庭投资房地产有其现实需求，但更多的是一种无奈。在当前金融市场还不够成熟，可投资金融资产种类偏少，相关法律法规还有待补充完善的情况下，投资房地产成为为数不多的“合理”选择，而这也造成了我国房地产行业的非理性繁荣，过度的投机炒作使得房价远偏离合理的区间，房地产市场泡沫化严重。[10]为了房地产行业的健康可持续发展，用期权的思维去解决当前的高房价难题可以说具有一定的可行性与必要性。

一、文献综述

由于期权本身是为了规避风险而为世人所创造的，所以对具有较强波动属性的资产的风险进行管理与控制成为了期权的主要目标。而房地产也属于波动性与风险较大的一类资产，所以国内外的很多学者都认为可以运用期权的思想来解决房地产行业的问题：Ciurlia发现由于房地产期权会受到做空的限制，所以风险中性定价方法等传统金融期权定价方法就不再适用于对房地产等实物资产的定价；[11]Levin通过研究通货膨胀率与房地产价格升值率之间的关系，认为房地产价格中的噪声因素服从正态分布，房地产价格会围绕均衡水平永久保持上下波动；[12]唐建立在系统性地研究了在房地产项目投资决策中期权的运用价值与潜力，通过实证证明了期权能够为房地产行业提供更多的投资决策依据；[13]秦笙等通过对中国市场以房地产标价物的期权进行实证研究，发现房地产期权能够实现对冲房价上涨，缓解短期购房压力，以及转变传统购房观念的作用；[14]何晋认为，由于政府的宏观干预的存在，模糊化的实物期权不适用于中国的房地产市场，相关定价参数也难以确定；[15]杨春梅等利用金融工程技术，将房地产融资租赁合约中隐含的奇异实物期权提炼出来并进行了期权定价推导与研究。[16]

综上所述，已有的文献与研究成果主要是从实物期权的定价形成机制来对房地产期权进行研究，因为有的学者认为模糊化的实物期权不适于中国的实际情况，所以就有部分学者试图从奇异期权的角度来看待这一问题，但是他们大部分都是在期权的定价方面作研究，对于期权在未来的投资策略以及在风险对冲中的应用没有更为深入的研究。所以本文将从期权控制风险的本质出发，将期权思想应用于房地产行业，通过设计一款经过改良的房地产奇异期权，帮助房地产行业化解可能产生的市场价格风险以及流动性风险，从而进一步降低系统性风险发生的可能性，这在维持房地产行业持续健康发展中将会发挥重要作用。

二、房地产奇异期权设计研究

(一)研究背景

期权在传统金融市场中属于金融衍生品的范畴，金融衍生品总的来说提高了金融市场的配置效率，通过对风险的分解与转化，将风险转移给那些愿意承担的市场参与者，从根本上改善了金融体系的资金利用效率。[17]我国的金融衍生品市场在近年来取得了长足的进步，股指期权、商品期货期权等传统的期权已经在交易所挂牌上市并取得了良好的经济与社会效应。而将期权应用于实务领域我们也进行了一些实践性的探索。由于中国房地产市场已具有一定的成熟性，适合针对特殊的市场需求推出相适应的房地产衍生产品，[18]而在目前已有的实物衍生品中，鄂尔多斯市的“房票”政策，即房屋兑换凭证，是一种针对性较强且应用较为成功的房地产衍生产品。[19]其目的是为实现当地房地产市场的有效去库存，增强房地产市场流动性，其主要内容是以“房票”作为对棚户区拆迁户的货币补偿的替代，拆迁户凭此“房票”可以自主选房，地方政府再利用国家棚改优惠政策获得政策性贷款去回购开发商已建、在建，甚至烂尾停工的商品房项目，而房地产企业也可以拿“房票”去银行抵债。这种将房产根据面积确定面值，并进行货币化标准化交易的房地产衍生产品为鄂尔多斯市实现去化33万平方米。所以，在当前房地产衍生产品还尚未完全推广之际，受到鄂尔多斯“房票”的启发，研究一款适用范围更广且更加符合中国广大地区实际情况的房地产衍生产品就具有一定的可行性。

(二)设计理念

由于期权自身的特性使得其能够有效地对冲因为房地产价格剧烈变动所产生的风险，所以我们认为在当前房地产衍生产品的设计与应用中，期权相对于其他衍生工具更加符合房地产行业的迫切需求。[20]对于当前房地产市场中的一些有非刚性需求的房产购买者来说，其购房行为更多的是由投机性因素所驱使。传统的房地产交易模式一是全额付款，二是支付一定比例的首付款再进行贷款补差，这两者都缺乏流动性，容易造成投机需求的非理性增长进而引发房价的不稳定波动。[21]本文想在传统的房地产交易模式的基础上给房产交易市场带来更多灵活的选择，于是我们从期权这一金融衍生品的角度出发，在传统欧式看涨期权的基础上，对传统的期权进行了分解与改进，使其能尽量贴近我国当前房地产行业的实际情况，设计出一款以锁定特定期限购房权利、以期权到期日房产价格为执行价格的奇异期权。

(三)设计思路

对于一套标准化房产来说，在房地产奇异期权到期前(即期权存续期内)，房产拥有者(即期权出售者)将暂时让渡房产出售权以获取期权费，若期权购买者最终决定行使权利，按照合约规定购买房产，房产拥有者将以期权到期日市场价格出售房产给期权购买者，而期权购买者支付的最终现金流是到期日当日房产市场价格与房地产奇异期权真正价值的差额。

同时，房产拥有者在暂时让渡房产出售权(即期权购买者在获得特定期限房产购买权)时，可以将房产以合约签订时市场价格按期租给期权购买者，而期权购买者租下房产并按期支付租金(即房产现金流)。

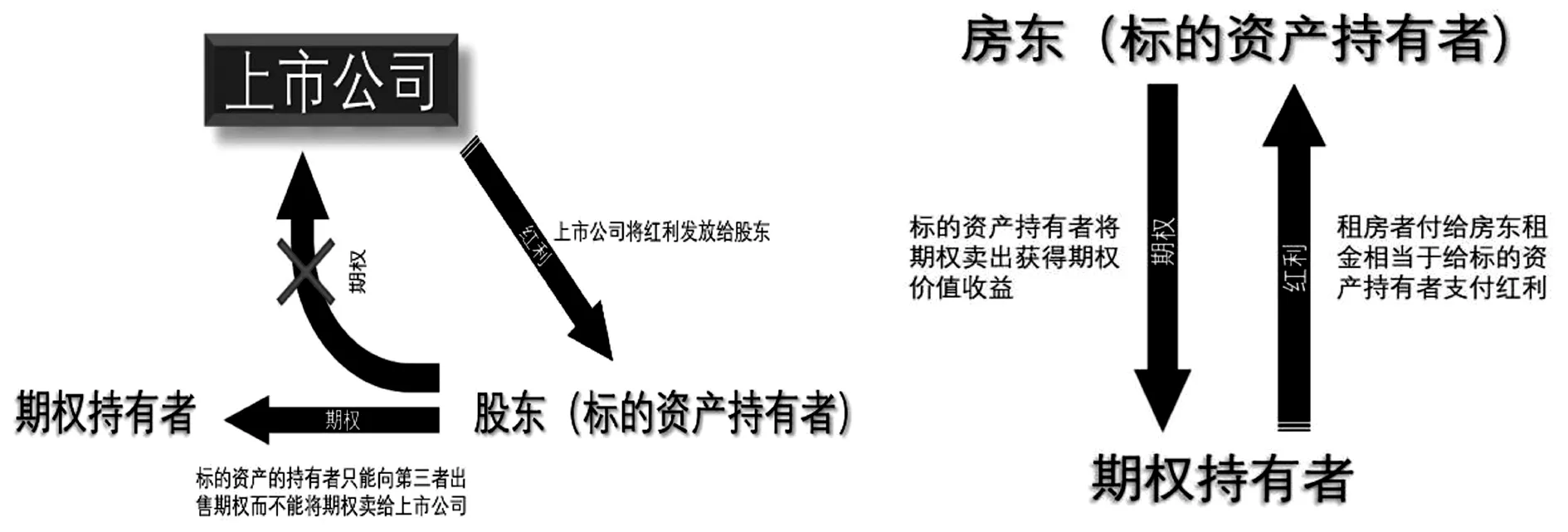
图1 普通股票期权与房地产奇异期权现金流模式对比

值得注意的是，该种房地产奇异期权的现金流方向也有别于一般标准股票期权的分红现金流，如图1所示，一般股票分红是上市公司向当期股票持有者发放红利，对应于股票期权在定价时，标准的有现金收益的布莱克-斯科尔斯-默顿期权定价公式将扣除现金分红。而该种房地产奇异期权的现金流模式是，期权购买者(房产租用者)向期权出售者(房产拥有者)支付租金现金流，房产拥有者既向期权购买者出售期权又向其收取租金现金流，这与普通股票的现金流模式有本质的不同，因为收取现金股利的股票持有者无法直接向发放现金股利的上市公司定向出售以该公司股票为标的的期权。其次，现金股利将会影响普通股票价格，一般股利发放后股票价格将下跌；但租金现金流的收入并不会降低甚至改变房产价格，虽然房产价格正向影响租金现金流，但从租金对房产价格的反向影响看，租金的收取独立于房产价格，即房产现金流与房产价格是相互独立的。

如上所述，在用布莱克公式计算房产拥有者让渡房产出售权的价值时，将不再考虑租金现金流问题。但与此同时还需要考虑房产拥有者在期初就卖出房产并在等同于期权存续期的时间内以无风险利率进行投资的机会成本。所以在房产同时被租给期权购买者的前提下，房地产奇异期权的真正价值是首先计算期权存续期内每期租金现金流现值之和，然后再计算房产拥有者在期初就卖出房产并在等同于期权存续期的时间内以无风险利率进行投资的净投资所得现值之和，接着对比这两种现值之和中的较大一者，最后将该较大者加上布莱克公式计算出的房产拥有者让渡房产出售权的价值之和即为房地产奇异期权的真正价值。

因此这款房地产奇异期权为期权购买者(即期权到期后或将购买房产者)锁定未来特定期限的房产购买权，其中未来特定期限为房地产奇异期权的存续时期，期权购买者只能在期权到期日行使权利来决定是否按照期权合约购买房产(类似欧式期权在到期日行权)。同时，对于期权购买者来说，拥有期权代表其已经锁定未来特定期限内的房产所有权，其他市场购买者不再拥有被该房产期权合约锁定的房产购买权。

同时，该种房地产奇异期权将以期权到期日房产价格为执行价格，即执行价格不在期权合约生成时固定，而在合约到期时以当日房产市场价格作为期权执行价格，若期权购买者在到期日决定行权，将依然以到期日当日房产市场价格购买期权合约所规定的房产，其支付的最终现金流是到期日当日房产市场价格与房地产奇异期权真正价值的差额。

(二)期权预期收益

首先，对于期权出售者(即房产拥有者)来说，在合约签订首日将获得以期权存续期为时限的所有租金的现值之和以及让渡以期权存续期为时限的房产出售权的价值。当房价在期权存续期内上涨时，期权出售者依然可以以期权到期日的房产价格出售房产，获得到期日当日房产市场价格与房地产奇异期权真正价值的差额，加上期初所得的租金现值与期权费以无风险利率进行投资的回报，其所得收入将高于在期权到期日直接出售房产所得；当房价下跌时，期权出售者的所得收入之和仍将高于在期权到期日直接出售房产所得，特别是对于并无在期初出售房产意愿而又缺乏现金流的期权出售者(即房产拥有者)来说，暂时让渡以期权存续期为时限的房产出售权以获得超过一般租金现值的超额资金补偿，是十分有利的选择。若期权购买者在期权到期日放弃购买权，期权出售者也已经获得期权费的回报，到时只需自由处理房产即可。

其次，对于期权购买者(即未来买房者)来说，在合约签订首日将支付以期权存续期为时限的所有租金的现值之和以及根据合约所获得的以期权存续期为时限的房产出售锁定权的价值。对于现在无能力直接购买房产而又选择暂时租用房产，未来决定购买该套房产的期权购买者来说，其在购买期权后，既能获得相同于期权存续期的房产租用权，提前入住，又能在期权到期日时，以到期日当日房产市场价格与房地产奇异期权真正价值差额的优惠价格购买房产，其超额支付的仅仅是房产出售锁定权的价值部分，无论未来房产价格上升还是下降，对期权购买者而言都是很好的选择。若期权购买者最终放弃行权，其最多损失期权费，即房产拥有者让渡房产出售权的价值。

三、房地产奇异期权定价

根据上文奇异期权的设计思路，我们在传统BSM的基础上进行了改进，虽然沿用了大部分的基本假设，但是对传统期权定价模型中的标的资产收益率K与期权价值f进行了重新的定义，并且定义了本房地产奇异期权的真正价值C，基本参数设置如下：

Ci：每期租金率；T：奇异期权到期日；S0：奇异期权发行首日的标的资产价格；St：奇异期权到期日标的资产价格；X：奇异期权名义执行价格(奇异期权到期日的标的资产价格)；Rf：无风险利率；σ：房产波动率；K：租金现值(标的资产收益率)；V：机会成本的现值收益；Ri：标的资产每期期望收益率；f：房产拥有者让渡房产出售权的价值；C：房地产奇异期权的真正价值；M：到期期权购买者到期行权时实际支付现金流；N(d1)、N(d2)：累积正态分布概率。

其中：房地产奇异期权存续期内每期租金现值之和为：

房地产奇异期权在售出期权合约时卖出房产并将该笔出售房产所得资金在期权存续期内以无风险利率进行投资的机会成本的现值收益为：

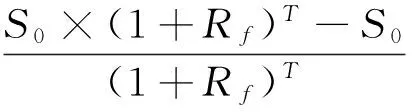
房地产奇异期权用布莱克公式计算出的房产拥有者让渡房产出售权的价值。

首先计算d1与d2：

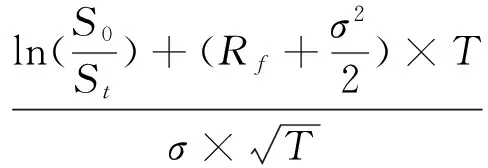
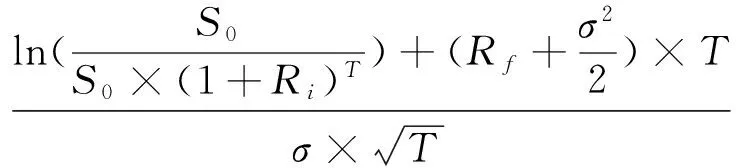
房产拥有者让渡房产出售权的价值：

f=S0×N(d1)-X×e(-Rf×T)×N(d2)

=S0×N(d1)-St×e(-Rf×T)×N(d2)

=S0×N(d1)-S0×(1+Ri)T×e(Rf×T)×N(d2)

其中，N(x)为累积正态分布概率，即：

所以综上所述，房地产奇异期权的真正价值应为：

C=max(K,V)+f

如果在期权到期日期权购买者行使权利，其到期支付现金流M应为：

M=Si-C=S0*(1+Ri)T-max(K,V)-f

四、房地产期权模拟分析

(一)参数赋值

为了能够对本房地产奇异期权进行进一步的分析研究，本文根据实际情况对期权各个参数进行适当的赋值，赋值结果如下：Ci：每期租金回报率=投资回报率=年租金/总房款×100%，据统计2016年我国省会城市平均房价为10000元/平米，并假设标准房屋100平米，月租4000元/月，则租金回报率=4000*12/10000*100*100%=4.8%；S0：奇异期权发行首日的标的资产价格为10000*100=1000000元；Rf：无风险利率=国债收益率，2016年3月发行一年期国债，其收益率为3.7%；Ri：标的资产每期期望收益率(平均增长率)，根据2016年6月统计数据，全国省会城市平均房价年增长率8.6%；σ：根据统计数据计算结果，2016年我国房价平均波动率在25%；T：期权存续期：1-10年。

(二)模拟结果

在以上参数设置下，用R语言计算其结果如表1所示，其中符号意义如下：Time：T，为期权存续期；Presentvalue：K，为租金现值(标的资产收益率)；Optcost：V，为机会成本的现值收益；K_to_V：max(K,V)，为K与V中最大值；Optionvalue：f，为房产拥有者让渡房产出售权的价值；Sum：C，为房地产奇异期权真正价值。

表1 不同期权存续期计算结果

(三)图形展示

图2中的三幅图横坐标都为T，即房地产奇异期权存续期都为1-10年，图2-(a)纵坐标为每一期期权存续期内所有租金现值之和；图2-(b)纵坐标为每一期房产拥有者让渡房屋出售权的价值；图2-(c)纵坐标为每一期房地产奇异期权的真正价值，即C=max(K,V)+f。

图2 房地产衍生产品在不同期限下的现金流

(四)结果分析

根据以上分析，其展示了房地产奇异期权1-10年不同期限的租金现值之和、机会成本的现值收益、房产拥有者让渡房产出售权的价值，以及房地产奇异期权真正价值等一系列房地产奇异期权的结构组成。为使产品结构更加清晰直观，我们用表1中的数据结果来进行分析。如果期权购买者(即未来买房者)购买3年期的房地产奇异期权(即表1的第三行)，其在合约签订日将向期权出售者(即房产拥有者)支付3年的租金现值之和与房产拥有者让渡3年房产出售权价值的总和，据以上计算，该总和值为265246.00元，其中3年的租金现值之和(K)为145526.90元，3年无风险投资的机会成本现值(V)为103265.80元，因为K>V，故取K=145526.90元，同时房产拥有者让渡3年房产出售权的价值(f)为119719.10元，所以房地产奇异期权的真正价值(C)为265246.00元，即C=K+f。若期权购买者在期权到期日行使权利，将以到期日当日房产市场价格与房地产奇异期权真正价值的差额现金流(M)购买房产，即(M=St-C)；若期权购买者在期权到期日放弃行使权利，则最多亏损房产拥有者让渡3年房产出售权的价值(f)为119719.10元。所以，在房价稳定、下降或均匀上涨的市场条件下，房地产奇异期权的购买者所支付的成本都小于银行贷款买房的成本之和。房地产奇异期权对期权购买者所提供的灵活选择权，以及给期权出售者所带来的期初现金流回报，增加房地产市场流动性都使得这款房地产衍生产品极具现实意义与价值。

五、结束语

本文所阐述的房产奇异期权能够给予房产交易市场带来更多灵活的选择，同时对于房地产市场稳定，抑制房价快速增长具有重要作用。根据本奇异期权的特性，从房产市场供求角度来看，当房产市场快速升温，房价大幅上涨时，期权购买者在期权到期时可能因房价过快上升，超过其预期支付水平而放弃行权，在其可将标的房产二次出租的情况下，最多仅损失期权费，但高企的房产市场可能会因为过多期权购买者的放弃行权而升势受阻，从而抑制房价过快上升；当房产市场出现震荡回调，房价下跌时，期权购买者因本身已支付期权费，在期权到期日房产价格低于购买期权时的价格时，可将此期权看作实值期权，为尽可能减少期权费损失，大多数期权购买者将会执行期权购买房产，此时房价会因多数期权的到期执行购买房产而止跌企稳，以此防止房产市场的断崖式下跌，为市场调节房产市场稳定起到关键作用。所以该奇异期权能够在一定程度上减少期权的购买者与出售者面临的价格波动，能够在一定程度上对冲因房价剧烈波动所造成的风险。在规避风险的同时转变普通购房者的观念，抑制恐慌性购房行为，减少房地产行业的非理性投机，促进房地产行业朝着更加健康的方向发展。

[1] Black, Fischer, and Myron Scholes. "The pricing of options and corporate liabilities." Journal of political economy 81.3 (1973): 637-654.

[2] Merton, Robert C. "Theory of rational option pricing." The Bell Journal of economics and management science (1973): 141-183.

[3] Cox, John C., Stephen A. Ross, and Mark Rubinstein. "Option pricing: A simplified approach." Journal of financial Economics 7.3 (1979): 229-263.

[4] Figlewski, Stephen, and Bin Gao. "The adaptive mesh model: a new approach to efficient option pricing." Journal of Financial Economics 53.3 (1999): 313-351.

[5] Longstaff, Francis A., and Eduardo S. Schwartz. "Valuing American options by simulation: a simple least-squares approach." Review of Financial studies 14.1 (2001): 113-147.

[6] Chernov, Mikhail, and Eric Ghysels. "A study towards a unified approach to the joint estimation of objective and risk neutral measures for the purpose of options valuation." Journal of financial economics 56.3 (2000): 407-458.

[7] Luehrman, Timothy A. "Strategy as a portfolio of real options." Harvard business review 76 (1998): 89-101.

[8] 夏健明,陈元志.实物期权理论评述[J].上海金融学院学报,2005,(01):4-13.

[9] 李梦玄,曹阳.我国房地产市场泡沫的测度及成因分析——基于行为金融理论的视角[J].宏观经济研究,2013,(09):86-91.

[10] 贾生华,李航.噪声交易者预期与房地产泡沫——基于35个大中城市的实证研究[J].审计与经济研究,2014,(03):85-92.

[11] Ciurlia, Pierangelo, and Andrea Gheno. "A model for pricing real estate derivatives with stochastic interest rates." Mathematical and computer modelling 50.1 (2009): 233-247.

[12] Levin, Eric, Alberto Montagnoli, and Robert E. Wright. "Demographic change and the housing market: evidence from a comparison of Scotland and England." Urban Studies 46.1 (2009): 27-43.

[13] 唐建立.实物期权在房地产投资决策中的应用研究[D].重庆大学,2003.

[14] 秦笙,陈阳,袁放建.基于中国市场的房地产期权研究[J]. 工业技术经济,2011,(08):156-160.

[15] 何晋.基于实物期权理论的房地产开发投资决策应用研究[D].西南财经大学,2012.

[16] 杨春梅,梁朝晖,王宗胜.创新的融资租赁定价研究——基于复杂实物期权的组合分解方法[J]. 价格理论与实践,2015,(03):90-92.

[17] 郭俊梅.我国金融衍生品市场的发展研究[D].首都经济贸易大学,2008.

[18] 杨光,孙伍琴.房地产衍生品研究文献综述[J].特区经济,2015,(09):151-152.

[19] 王杰.鄂尔多斯“房票”：6.7折卖 去化33万平方米[N].每日经济新闻,2016-10-10(003).

[20] 毛英英.实物期权在房地产投资中的应用[D].华中师范大学,2014.

[21] 曹晓元.基于行为经济学的房地产投机行为研究[D].华中师范大学,2006.

责任编辑：王明舜

A Study on Real Estate Exotic Options Based on BSM Model

Shu Jiaxian Wu Hangyu Jin Zijie

(School of Finance, Anhui University of Finance and Economics, Bengbu 233030, China)

This paper rethinks the high housing price problem in China with the thinking of the option, and improves it according to the actual situation of the traditional BSM in the current real estate market. We design a lock to a certain period of time to purchase the right to the option date of the real estate prices for the implementation of the price of the exotic options to ease the speculative demand caused by high housing prices.

real estate; BSM option pricing model; exotic option pricing

2016-12-16

舒家先(1975- )，男，安徽太湖人，安徽财经大学金融学院副教授，主要从事证券投资理论研究。

F830.9

A

1672-335X(2017)03-0040-06