一种在Fluent UDF中使用IMSL Fortran数值库的方法*

胡文清，詹杰民

(中山大学工学院应用力学与工程系，广东 广州 510275)

一种在Fluent UDF中使用IMSL Fortran数值库的方法*

胡文清，詹杰民

(中山大学工学院应用力学与工程系，广东 广州 510275)

UDF能极大地延伸Fluent的功能，被广泛应用于Fluent的各类计算中。IMSL是一个集合数学与统计函数的程序库，具有高效率、性能强大、应用简单等优点。研究并找到了一种方法，通过将调用IMSL的Fortran程序编译为动态链接库，并在UDF中调用该动态链接库，实现在UDF中使用IMSL数值库；同时给出了一个实例，在数值水槽中生成椭圆余弦波。为结合IMSL的优点，实现更简单、更快速、更自然的UDF程序编写提供了技术支持，极大地提高了复杂UDF的编写能力，增强Fluent的计算能力和应用范围。

Fluent；UDF；IMSL；Fortran；椭圆余弦波

在计算流体动力学领域的众多计算软件中，Fluent是目前国内外使用最多、 最流行的商业软件之一。对于复杂几何体的流体流动和传热的模拟问题，Fluent更是达到世界顶尖的水平。Fluent是用C语言编写而成的，充分利用了C语言所提供的灵活性和强大的功能。在Fluent的众多功能中，最能体现这一特点的，是用户自定义函数，即UDF(User-Defined Function)这一功能。UDF为一段C语言函数程序，可以被Fluent求解器动态加载，用于增强Fluent的标准功能，如自定义边界条件、自定义材料属性、为流域添加源项、自定义计算模型参数等[1]。因此，UDF在Fluent的各类计算中被广泛使用[2]。

IMSL(International Mathematics and Statistics Library)国际数学和统计程序库是在国内外广泛使用的集合数学与统计函数的综合性的程序库，应用范围广泛，具有规模大、结果可靠、内容丰富、应用简单、程序运行效率高等优点。IMSL拥有众多的发行版本，其中最悠久，也是应用最广泛的是IMSL Fortran数值库这一版本。最早的IMSL Fortran数值库于1970年发行，历经40余年的优化，使其拥有极高的计算精度和稳定性[3]。这版本使用Fortran语言开发，Fortran语法简明严谨，接近数学公式的自然描述，可以直接对矩阵和复数进行运算，在计算机里具有很高的执行效率。IMSL Fortran数值库拥有超过1000种函数，能直接嵌入程序中使用，同时支持并行计算而且线程安全，为程序编写提供了更简单、更快、更自然的方法。

由于Fluent是C语言编写的，UDF也只能用C语言编写。而IMSL Fortran数值库是Fortran编写的，因此也只能在Fortran程序中使用，但仍然有在其他环境中使用该库的方法[4-5]。曾经有研究人员结合了Fluent和IMSL数值库进行研究，但其没有给出具体实现过程[6]。C和Fortran的混合编程方法已有多人进行研究[7-8]，在C里调用Fortran IMSL库也给出了实现方法[5]，但UDF有其特殊性，不能直接使用已有方法。为了实现在UDF中使用IMSL Fortran数值库，本文提出了一种方法，具体的实现流程为：将需要调用IMSL Fortran数值库的功能利用Fortran语言编写，将其编译成动态链接库(Dynamic Link Library)，在UDF中采用静态调用该DLL，以达到在UDF中使用IMSL Fortran数值库的效果。

本文研究的开发平台为64位WIN7，Fortran为Intel(R) Visual Fortran Compiler Professional 11.1.038 + Microsoft Visual Studio 2008，IMSL为IMSL(R) Fortran Numerical Library Version 6.0.0 for Intel(R)64，Fluent为ANSYS Fluent 15.0。

1 Fortran调用IMSL Fortran的实现方法

IMSL Fortran数值库安装后有DLL和Static两种版本，默认的配置是使用DLL的版本。为了能尽量简化操作，本文使用的是DLL的版本。在Fortran程序中调用IMSL Fortran数值库，需要在程序的开头添加以下代码段[9]：

include 'link_fnl_shared.h′

这个头文件是使用IMSL Fortran库的DLL版本所必需的。之后，根据实际使用需求，利用use语句使用IMSL Fortran数值库里的各类模块。

Fortran程序的默认调用约定与UDF所用的C语言的调用约定不同，因此需要在Fortran程序中保证调用约定的匹配。Fortran一共有三种调用约定，C、STDCALL、Default，其中C调用约定就是和C语言所匹配的调用约定。因此在Fortran处不采用默认调用约定，而是使用C，与C语言相匹配，这需要在Fortran程序中声明[10]。

为了在UDF中调用Fortran程序，需要将Fortran程序编译成DLL的形式。由于本文使用的Fluent为64位版本，因此需要使用x64平台来编译该DLL。Fortran编译DLL时，可以采用function或者subroutine形式。由于subroutine可以利用虚参实现多个返回值，因此一般采用subroutine形式。以下是本文实例的Fortran部分代码段，定义了一个名为“calscdn”的过程，该过程存储与名为“Dll1”的DLL文件中，用于计算雅可比椭圆函数：

subroutine scdn(x,t,k,sn,cn,dn)

!DEC＄ATTRIBUTESC,DLLEXPORT::scdn

!DEC＄ATTRIBUTES ALIAS:"calscdn"::scdn

!DEC＄ATTRIBUTES VALUE::x,t,k

!DEC＄ATTRIBUTES REFERENCE::sn,cn,dn

include 'link_fnl_shared.h′

use elk_int

use ejsn_int

use ejcn_int

use ejdn_int

implicit none

real(8)::x,t,k,sn,cn,dn,kk,tx

kk=elk(k**2)

tx=2.d0*kk*(x-t)

sn=ejsn(tx,k**2)

cn=ejcn(tx,k**2)

dn=ejdn(tx,k**2)

end subroutine scdn

其中，!DEC＄ATTRIBUTES语句用于定义该DLL工程的属性。C定义了该子过程使用C调用约定，DLLEXPORT表明该子过程能被外部其他程序或DLL调用。ALIAS属性定义了该子过程的别名，将编译产生的目标例程名限定为引号内的名称，以保持大、小写混合。使用ALIAS属性避免了在UDF的部分必须使用符合C调用约定的例程名称，而是能按程序员个人的意愿决定该子过程的例程名。VALUE和REFERENCE定义了该子过程的参数是按值传递还是按地址传递。C调用约定的默认参数传递约定是按值传递，而VALUE和REFERENCE属性的定义会覆盖调用约定对参数传递产生的影响，因此推荐将全部参数都显式定义其参数传递方式。

这段代码利用use语句使用了IMSL Fortran数值库的四个模块，分别用于计算第一类完全椭圆积分、雅可比椭圆函数sn、cn、dn。这段代码清楚地显示了使用IMSL Fortran数值库所带来的优势，让程序编写更简单、更快、更自然。

2 UDF调用Fortran DLL的实现方法

UDF是用C语言编写的一段代码，与一般的C程序相比，UDF具有自己的特点：必须包含“udf.h”头文件；必须使用Fluent提供的DEFINE宏来进行定义；通过Fluent预定义的宏和方程获取Fluent求解器的数据等[1]。对于一般的C程序，其调用DLL有动态链接和静态链接两种方法[11]。其中动态链接需要使用Windows的API，而鉴于UDF的特点，这点并不能实现。因此本文采用静态链接的方法实现对Fortran DLL的调用。在Fluent中，使用UDF有两种方式，分别为解释型和编译型。为实现调用DLL，必须使用编译的方法使用UDF。

在UDF中调用DLL，需要将被调用的DLL文件本身和对应的Lib文件，分别复制到指定的文件夹中，包括Fluent项目的工作目录，和此工作目录下UDF编译后产生的UDF文件夹中。以一个二维双精度的Fluent项目为例，编译出的UDF默认名字为libudf，在工作目录下会有以此名字命名的文件夹，内有src和win64两子文件夹，在win64文件夹内有1到3个文件夹，包括单线程使用的2ddp文件夹和多线程使用的2ddp_host和2ddp_node文件夹。如果是三维Fluent项目，则上述文件夹名称里的2d改为3d，单精度项目则是将上述文件夹名称里的dp去掉。为成功编译UDF，需要将DLL文件和对应的库搜索记录Lib文件，分别复制一份到Fluent项目的工作目录，和上述的单线程时2ddp文件夹，多线程时2ddp_host文件夹和2ddp_node文件夹中。

以下为本文实例的UDF部分代码段，调用了本文第二部分实例给出的Fortran过程，用于给定数值水槽入口处的水相的体积分数：

#include "udf.h"

#pragma comment(lib,"Dll1.lib")

extern voidcalscdn(double x,double t,double k,double*sn,double*cn,double*dn);

DEFINE_PROFILE(inlet_w_vof,thread,index)

{

double x[ND_ND];

double zs,z;

double ct,sn,cn,dn;

face_t f;

ct = CURRENT_TIME;

sn=0;

cn=0;

dn=0;

calscdn(0./L,ct/T,K,&sn,&cn,&dn);

zs=Zt+H*cn*cn;

begin_f_loop(f,thread)

{

F_CENTROID(x,f,thread);

z=x[1];

if(z<=zs)

F_PROFILE(f,thread,index) = 1.;

else

F_PROFILE(f,thread,index) = 0.;

}

end_f_loop(f,thread)

}

其中，#pragma是一种预处理指令，起到设定编译器的状态或指示编译器完成特定动作的作用。#pragma comment (lib,"Dll1.lib")命令使对象工程链接Dll1.lib这个库搜索记录，该命令的作用与在工程设置里修改设置是相同的，使用该命令，就不需要修改UDF的编译文件，能有效地简化操作。extern语句声明了calscdn过程是外部过程，后面的参数定义和顺序需要跟Fortran程序中的完全一致。

当使用多线程的Fluent时，以上的UDF使用Fortran DLL的方法仍然适用，唯一需要修改的是Fluent多线程使用的MPI类型。Fluent默认使用的MPI是PCMPI，由于IMSL Fortran数值库内部也调用了相同的MPI，若不作修改编译UDF，则会在Fluent计算时产生错误。因此使用多线程的Fluent时，为了防止计算时产生错误，需要将Fluent使用的MPI类型做出修改，例如改为Intel MPI。

3 在数值水槽中生成椭圆余弦波

波浪进入近岸浅水区后，海底边界的摩阻力迅速增加，波高和波形将不断变化，波面在波峰附近变得很陡，而两个波峰之间却相隔很长但又较为平坦的水面，波的运动特性与相对波长L/d的关系减弱，而与相对波高H/d的关系增强，即L/d和H/d都成为决定波动性质的主要因素。在这种浅水情况下，使用椭圆余弦波理论来描述波浪运动，可以取得较满意的结果。椭圆余弦波理论最早是在1895年由Korteweg与De Vries提出的，其后由Keulegan及Patterson，Keller，Littman，Wiegel等人进一步加以研究并使之适用于工程实践。椭圆余弦波的二阶近似波面方程为[12]：

(1)

其中，zt为波谷底与离水底的高度，d为水深，H为波高，L为波长，T为周期，k为波数，K为第一类完全椭圆积分，E为第二类完全椭圆积分，cn为雅可比椭圆余弦函数。由于在波面方程中出现了椭圆函数cn，故这种波浪被称为椭圆余弦波。波数k由以下公式决定：

(2)

波速c由以下公式决定：

(3)

水质点的运动速度分布为：

(4)

sn·cn·dn

式中

cn、sn和dn均为雅可比椭圆函数。

数值水槽的设计如图1所示。数值水槽长30 m，高1 m，水深0.4 m。左侧是速度入口，上方是空气的压力入口，右侧是压力出口下方是水槽底墙壁。水槽最后8 m为消波段，采用添加源项的方法消波[13]。采用VOF方法实现数值造波，在速度入口处分别给定流体的x方向速度、y方向速度和水的体积分数。

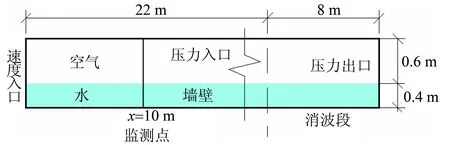
图1 数值水槽示意图Fig.1 Diagram of numerical flume

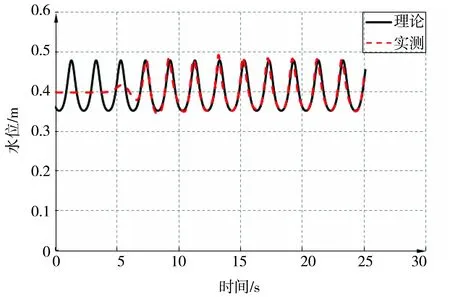
图2 测点x=10 m处水位变化对比图Fig.2 Comparison of water level change at measuring point x=10 m

本实例所造椭圆余弦波的参数为：周期T为2 s，波高H为0.127 m。具体的实现方法如下：

1)通过给定的椭圆余弦波参数周期T，利用公式(2)和(3)，根据波长L=cT，使用松弛迭代法计算波长L，波数k和zt。这部分使用Fortran编译为过程1，调用IMSL Fortran数值库以求解椭圆积分。

2)使用Fortran编写过程2，调用IMSL Fortran数值库，根据输入的参数，计算雅可比椭圆函数。该部分代码在本文第二部分的实例中给出。

3)编写UDF程序，在DEFINE_INIT宏中调用过程1以计算椭圆余弦波参数，使用DEFINE_PROFILE宏，调用过程2利用公式(1)和(4)，分别给定速度入口处的x方向速度、y方向速度和水的体积分数。其中调用Fortran过程的方法和给定水的体积分数部分的代码在本文第三部分的实例中给出。

在数值水槽中x=10 m的位置设置了监测点。图2为在x=10 m处的监测点上水位随时间变化的示意图。可以看到，所造出来的椭圆余弦波与理论值十分接近，可以认为这种方法是成功有效的。

4 总 结

本文详细介绍了一种在Fluent UDF中使用IMSL Fortran数值库的方法，并通过在数值水槽中生成椭圆余弦波的实例，给出了详细的实现过程。通过对Fortran调用IMSL Fotran数值库和UDF调用Fortran DLL的实现方法的研究，基本解决了在UDF中使用IMSL Fortran数据库可能出现的各种问题，从而为在64位平台上，利用IMSL Fortran的强大能力，增强和简化UDF的编写过程，有效地减低了UDF的编写难度，实现更简单、更快速、更自然的UDF程序编写，极大地提高了复杂UDF的编写能力，增强Fluent的计算能力和应用范围。

[1] ANSYS INC. Ansys 15.0 fluent UDF manual[M]. USA: Ansys Incorporated, 2013.

[2] 辛颖. Fluent UDF方法在数值波浪水槽中的应用研究[D]. 大连: 大连理工大学, 2013. XIN Ying. Application of fluent UDF method in the study of numerical wave tank[D]. Dalian: Dalian University of Technology, 2013.

[3] 董桂洪, 王胜年, 范志宏，等. IMSL C#数值分析函数库在混凝土技术中的应用[J]. 水运工程, 2010 (5): 61-64. DONG Guihong, WANG Shengnian, FAN Zhihong， et al. Application of IMSL C# numerical library to concrete technology[J]. Port & Waterway Engineering, 2010 (5): 61-64.

[4] STEWART E. Distributed IMSL with 3rd party solutions in C, Java and .NET[C] ∥ Proceedings of the 2006 ACM/IEEE Conference on Supercomputing. USA: ACM, 2006: 277.

[5] KIM J, ROBERTSON L M. How to call the IMSL Fortran libraries from C[R]. IMSL Technical Report Series, No. 8902. USA: Visual Numerics Incorporated, 2000.

[6] MUNTEAN S, SUSAN-RESIGA R F, ANTON I. Mixing interface algorithm for 3D turbulent flow analysis of the GAMM Francis turbine[C] ∥ VAD J, et al. Modeling Fluid Flow: The State of the Art. Berlin Heidelberg, Germany: Springer-Verlag 2004: 359-372.

[7] 任慧, 周振红, 张成才. Fortran与C/C++的混合编译[J]. 计算机工程与设计, 2007 (17): 4096-4098. REN Hui, ZHOU Zhenhong, ZHANG Chengcai. Mixed-language compiling between Fortran and C/C++[J]. Computer Engineering and Design, 2007 (17): 4096-4098.

[8] 周振红, 宋宇伟, 郭恒亮，等. Visual Fortran基于Win32 DLL的混合编程技术[J]. 郑州大学学报(工学版), 2003 (3): 10-13. ZHOU Zhenhong, SONG Yuwei, GUO Hengliang， et al. Mixed-language programming of Visual Fortran based on win32 DLL[J]. Journal of Zhengzhou University (Engineering Science), 2003 (3): 10-13.

[9] Visual Numerics Inc. IMSL Fortran numerical library version 6.0 user’s guide[M]. USA: Visual Numerics Incorporated, 2006.

[10] Intel Corp. Intel Fortran compiler 11.1 user and reference guides[M]. USA: Intel Corporation, 2009

[11] Microsoft Corp. Visual C++, Microsoft visual studio 2008 documentation[M]. USA: Microsoft Corporation, 2008.

[12] 邱大洪. 波浪理论及其在工程中的应用[M]. 北京: 高等教育出版社, 1985: 83-114. QIU Dahong. Wave theory and its application in engineering[M]. Beijing: Higher Education Press, 1985: 83-114.

[13] 陈学彬, 詹杰民, 苏炜. 相邻多浮体与波浪作用的共振物理现象数值模拟[J]. 中山大学学报(自然科学版), 2016, 55(1): 54-62. CHEN Xuebin, ZHAN Jiemin, SU Wei. Numerical simulation of resonance between adjacent multi-floating bodies and waves[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(1): 54-62.

A method of using IMSL Fortran numerical libraries in Fluent UDF

HUWenqing,ZHANJiemin

(Department of Applied Mechanics and Engineering, School of Engineering, Sun Yat-sen University, Guangzhou 510275, China)

UDF can greatly extend the functions of Fluent, is widely used in various types of Fluent calculation. IMSL is a set of mathematical and statistical libraries, with high efficiency, powerful performance, and simple application. A method is proposed to implement IMSL numerical libraries in UDF by compiling the Fortran program that calls IMSL as a dynamic link library and calling the dynamic link library in UDF. At the same time, an example is given to generate cnoidal wave in a numerical flume. It provides technical support for the realization of simpler, faster and more natural UDF programming with the advantages of IMSL, which greatly improves the compiling ability of complex UDF and enhances the computing power and application range of Fluent.

Fluent; UDF; IMSL; Fortran; cnoidal wave

10.13471/j.cnki.acta.snus.2017.03.005

2016-12-20 基金项目： 广东省协同创新与平台环境建设专项项目(2014B090904066)

胡文清(1987年生)，男；研究方向：流体力学；E-mail: emp_beren@163.com

詹杰民(1963年生)，男；研究方向：流体力学；E-mail: stszjm@mail.sysu.edu.cn

O353

A

0529-6579(2017)03-0031-05