三角恒等变换

云南省保山市第一中学(678000)

刘运铭●

三角恒等变换

云南省保山市第一中学(678000)

刘运铭●

在高中数学里，三角恒等变化是个涉及广泛的知识点，是三角函数式化简、计算、恒等式证明的主要环节，同时也是三角函数的一个重难点，今天我就交流一下，我认为在三角恒等变换中应该注意的方法与技巧.

一、角的变化与转换

在遇到的题目中经常会出现所求角和已知角不一样，一般会出现和差、倍半、互余、互补关系，通过变化与转换，统一已知角和所求角，再进行计算.

常见的角的变形有

α=(α+β)-β=β-(β-α)

2α=(α+β)+(α-β)

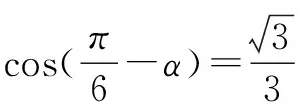
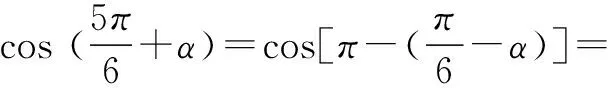
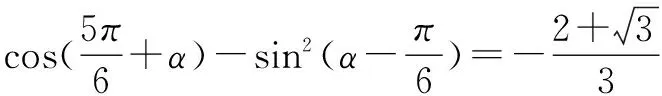
例2 已知tan(α+β)=3tan(α-β)=5则tan2α=____.

分析 已知角是 (α+β)和(α-β)，所求角是2α，2α=(α+β)+(α-β)

解 tan2α=tan[(α+β)+(α-β)]

二、对基础三角恒等式的应用

(1)三角恒等变涉及多种公式，但其中最为重要也是最基础的公式就是两个恒等式：

sin2α+cos2α=1

注意这两个公式的正用、逆用、变形应用.

(2)对于sinα+cosα，sinαcosα，sinα-cosα这三个式子，利用(sinα±cosα)2=1±2sinαcosα，可以知一求二.

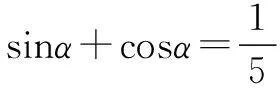
整理可得25sin2α-5sinα-12=0

∵α是三角形内角

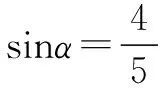
三、公式的变形运用

公式之间都是有着相互的关系，往往记住一个公式再通过变换，就可以记住其他公式.

四、解题的技巧性

(1)辅助角公式

对于形如asinx+bcosx的式子可以变形为：asinx+bcosx

(2)运用题目中的“1”解决问题

一个题目中往往会出现“1”，1=sin2α+cos2α=tan45°=sin90°=cos0°等等

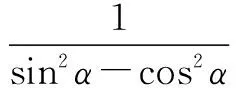
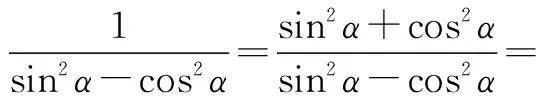
以上就是我在学习过程中总结出的一下解三角恒等变换的的方法与技巧.概括起来就是：在和差、倍半、互补、互余等关系下，利用和、差、倍角、半角、和差化积、积化和差等公式，进行相互转化，解决问题.

G632

B

1008-0333(2017)01-0035-02