问渠那得清如许为有源头活水来
——由课本例题探究有心圆锥曲线的性质及其应用
浙江省杭州市富阳区新登中学(311404)
陈国清●
问渠那得清如许为有源头活水来
——由课本例题探究有心圆锥曲线的性质及其应用
浙江省杭州市富阳区新登中学(311404)
陈国清●
一、例题展现

图1
人教A版数学选修2-1第41页例3

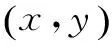

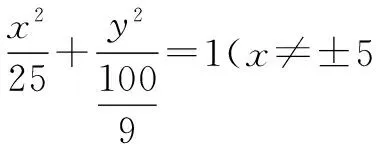
二、引申探究
探究1 斜率之积为常数的点的轨迹及常数与离心率的关系

探究 设动点P(x,y),两定点A1(-a,0)、A2(a,0),直线PA1、PA2的斜率之积k1·k2=t,求点P的轨迹,并探究t与离心率e之间的关系.
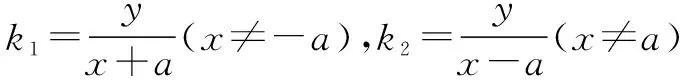
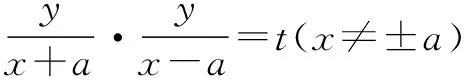
1°若t=0,方程为y=0(x≠±a),点P的轨迹为x轴(不包括A1、A2).
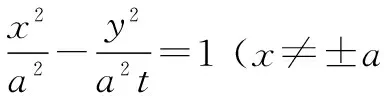
1若t>0,点P的轨迹是以A1A2为实轴的双曲线(不包括A1、A2);

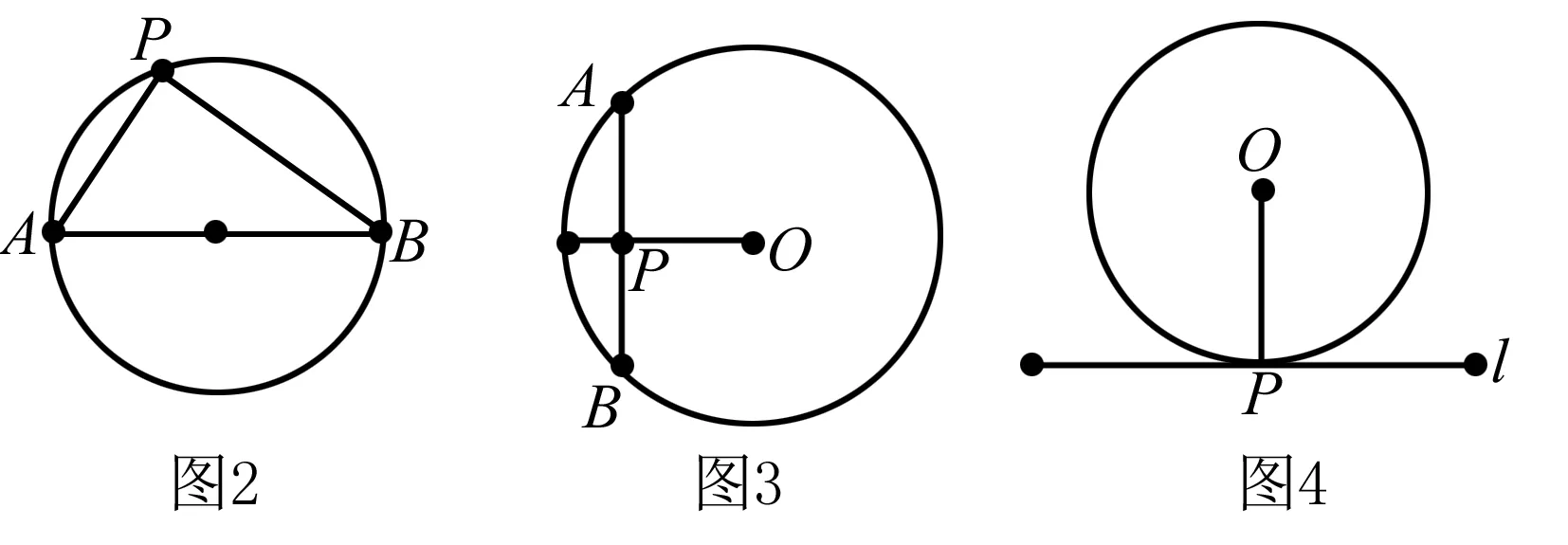
②若-1 ③若t=-1,点P的轨迹是以A1A2为直径的圆(不包括A1、A2); ∵圆的离心率e=0,∴t=e2-1. ④若t<-1,点P的轨迹是以A1A2为短轴的椭圆(不包括A1、A2); 因此,平面内与两定点连线的斜率之积为常数t的点的轨迹不一定是椭圆,但当t≠0时,它们同为有心圆锥曲线. 结论1 当t=-1时为圆;当t<0且t≠-1时为椭圆;当t>0时为双曲线. 探究2 圆的性质推广到其他有心圆锥曲线 圆具有以下性质: (1) 如图2,过圆心的直线l与圆交于A、B两点,P为圆上不同于A、B的任意一点,则PA⊥PB,即kPA·kPB=-1; (2)如图3,经过弦中点的半径OP与弦AB垂直,即kAB·kOP=-1; (3)如图4,过圆上任一点P引切线l,则OP⊥l,即kOP·kl=-1. 探究 椭圆、双曲线与圆同为有心圆锥曲线,是否具备类似性质?下面以焦点在x轴上的椭圆为例探究. 证明 设P(x0,y0),A(x1,y1),B(-x1,-y1),∵点A、P在椭圆C上, 证明 设P(x0,y0),A(x1,y1),B(x2,y2), 以上是焦点在x轴上的有心圆锥曲线,焦点在y轴上的有心圆锥曲线与此相似,不过此时结论为斜率倒数之积等于e2-1. 证明 设P(x1,y1),B(x2,y2),则A(-x1,-y1),C(x1,0). ∴kPA·kPB=2kAB·kPB=-1,故PA⊥PB. 点评 此题考查斜率的求法,以及直线与椭圆的位置关系,体现了方程思想和数形结合思想,难度较大.但如果了解了有心圆锥曲线的性质,题目便变得迎刃而解. 已知直线l的斜率为k,用a,b,k表示点P的坐标. ∵点P在第一象限,且k<0, 点评 此题如果联立方程利用Δ=0当然也可以做,但是计算量很大,用时较长;而利用椭圆性质,则简直可以秒杀.对于分秒必争的高考而言,哪种方法更好不言而喻. 通过课本例题探究有心圆锥曲线的性质,并利用性质解决高考题,我们可以从中得到以下启示: 1.对于一个数学问题,我们不仅要引导学生去探究方法的巧思妙解,更要引导学生探讨问题所蕴含的的数学本质,让题目会“说话”.例题课堂教学中不断变换角度,尽量发挥例题的辐射作用,是激活学生数学思维的一种重要途径.对例题进行引申探究,以期构建动态生成,继而挖掘其潜在的智能训练因素:或启迪思路,提炼方法;或引申问题,丰富内涵;或串联知识,扩大成果,从而彰显我们的数学智慧. 2.课本是最重要的教学资源,课本中的例、习题是编者依据课程标准精心挑选且具有代表性的问题,是问题中的精华,也颇受高考命题专家的青睐,所以说教材是高考命题的源头.面对高考,我们不仅要研究考试说明,更要重视教材,深入研究教材,挖掘题根,彻底了解问题的本质,这样才能以不变应万变,在高考中做到问渠那得清如许,为有源头活水来. [1]苏立标. 落霞与孤鹜齐飞 秋水共长天一色——2012浙江高考解析几何试题的本源探讨[J].中学数学(上),2012(9). G632 B 1008-0333(2017)01-0023-02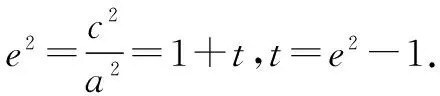
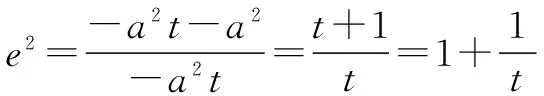
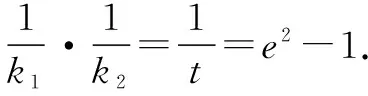

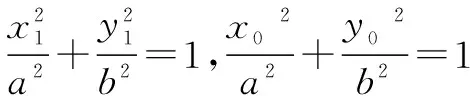



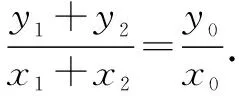
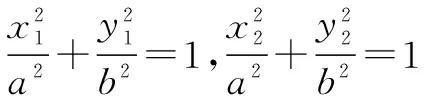
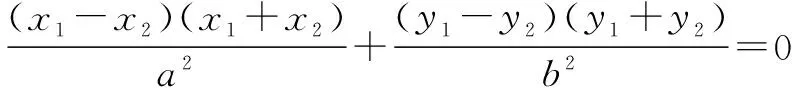
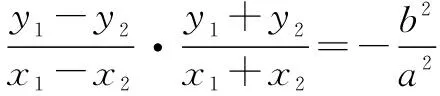
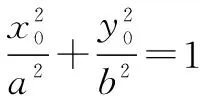

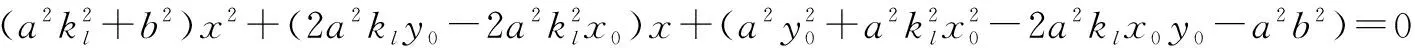
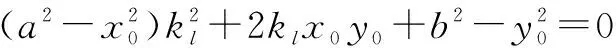
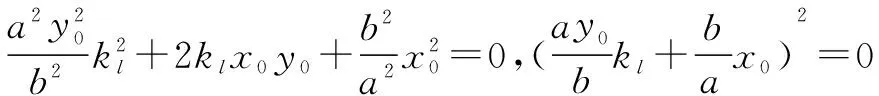
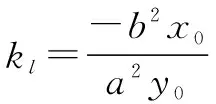
三、高考应用
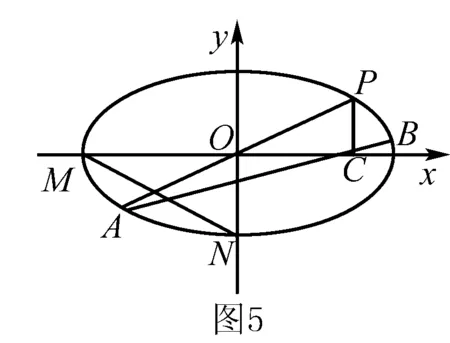
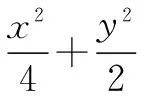

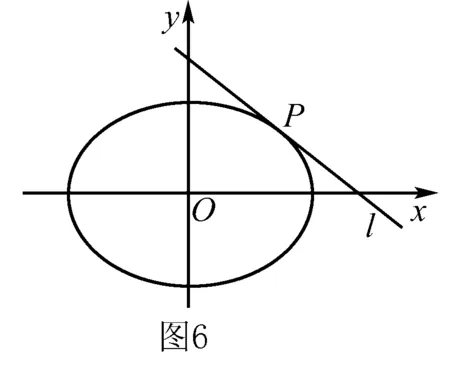

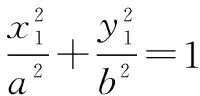
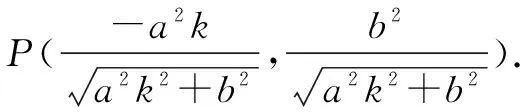
四、总结启迪

