数形结合思想在线性规划问题中的应用
河北省乐亭第一中学高三15班(063600)
李子健●
数形结合思想在线性规划问题中的应用
河北省乐亭第一中学高三15班(063600)
李子健●
由于在线性规划的知识中即具有数,也具有形,因此该知识点是数学中化数为形、以形解数、数形结合的思想的生动诠释.
一、线性规划基础问题中的数形结合
线性规划的基础问题包括求与直线截距、直线斜率和距离有关的最值问题,其解答一般步骤:1、画出可行域;2、明确目标函数的几何意义;3结合图形找最优解;4求目标函数的最值.
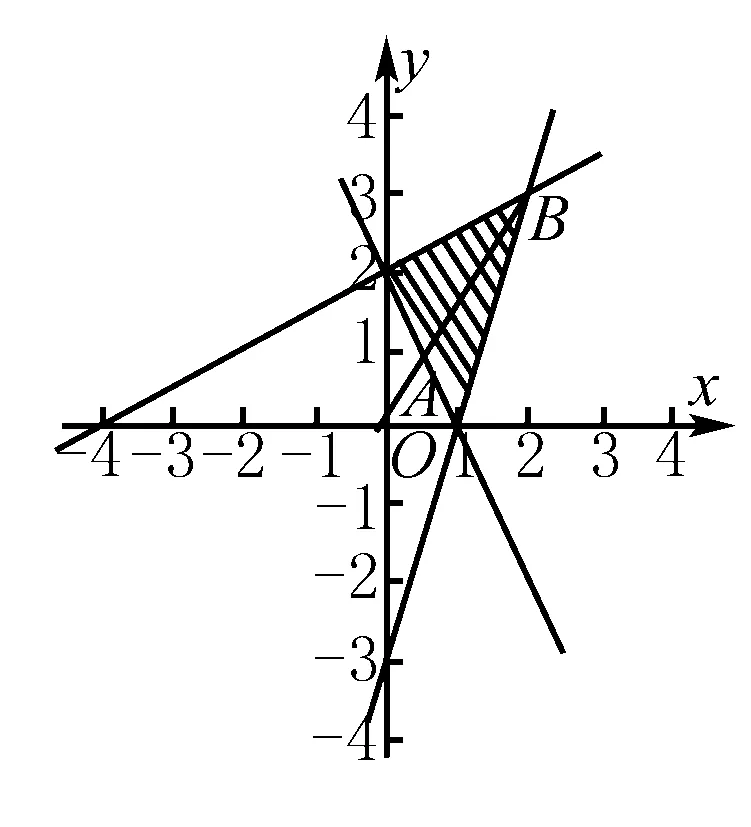
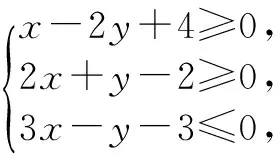
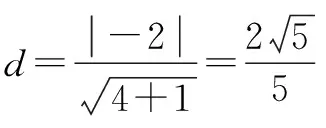
点拨 解决线性规划基础问题的精髓就是运用数形结合思想中的化数为形,画出约束区域,然后再从目标函数所表示的几何意义入手解题,使看似无法入手的线性规划问题,轻松解决.
二、线性规划简单应用中的数形结合
线性规划的简单应用就是线性规划知识在实际问题中的应用,即数学应用题,解答该类问题的一般步骤是:1.审题:明确限制条件和目标函数;2.转化:写出约束条件和目标函数;3.求解:明确目标函数的几何意义;4.作答:解答题目所提出的问题.

例2 生产1桶A产品各需要甲、乙料子1kg、2kg;生产1桶B产品各需要甲、乙料子2kg、1kg.每桶A、B产品的利润分别为300元、400元.公司要求每天的原料消耗不超过12kg.试问怎样规划每天生产的A、B两种产品的数量,从而使公司获得最大利润,最大利润是( ).
A.1800元 B.2400元 C.2800元 D.3100元

选C.
点拨 由例题可知,解决线性规划的应用题时,根据题目要求列出约束条件,然后运用数形结合的思想,从形的角度出发,画出可行域,从而为顺利解题打下基础.
3、线性规划综合运用中的数形结合
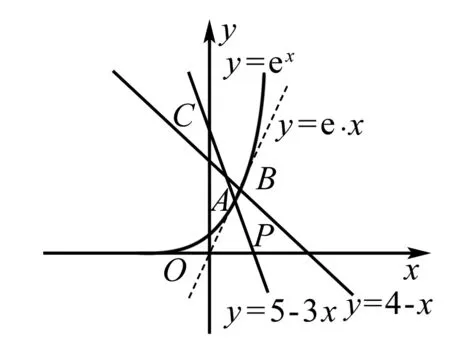
线性规划的综合运用的题目一般具有较强的迷惑性,其是以线性规划的知识为载体,通过创新的手法,将不等式、对数运算、导数等知识融合在一起,综合性强.该类问题在解答时很容易让人联想到用线性规划的知识并结合数形结合的思想切入,但是要想进一步深入就比较难.


点拨 由例题可知,解决线性规划综合运用的题目时,先要整体处理从而达到减少变量的目的,然后再运用数形结合思想中的以形解数,从而完整的解题思路即可揭开神秘的面纱.
综上所述,在解决线性规划的问题时,图形、几何意义是能否顺利解题的关键,而这两点正好是数形结合的思想的完美体现.因此,要想学好线性规划就必须要灵活运用数形结合的思想.
G632
B
1008-0333(2017)01-0040-01

