锥束X射线CT图像重建的新型滤波函数

洪振厚，周 彬，郭金川

深圳大学光电工程学院，光电子器件与系统教育部/广东省重点实验室，广东深圳518060

【光电工程 / Optoelectronic Engineering】

锥束X射线CT图像重建的新型滤波函数

洪振厚，周 彬，郭金川

深圳大学光电工程学院，光电子器件与系统教育部/广东省重点实验室，广东深圳518060

针对X射线计算机断层成像(computed tomography，CT)图像重建FDK算法中，采用通常的滤波函数会导致明显的Gibbs现象，影响重建图像的质量．基于混合滤波和加权平均理论，设计了一种新型的NEW-MS-L滤波函数．先将S-L滤波函数加权平均为M3S-L滤波函数，再与NEW滤波函数叠加,得到NEW-MS-L滤波函数．通过数值仿真，分别对比NEW、R-L-S-L、R-L-NEW、R-L-MS-L和NEW-MS-L滤波函数的重建图像效果，结果表明，NEW-MS-L滤波函数能够在保持较高图像分辨率的情况下，更有效地抑制Gibbs现象，使重建图像效果更佳．

光学工程；计算机断层成像；FDK算法；滤波函数；Gibbs现象；混合滤波；加权平均

随着计算机断层成像(computed tomography, CT)在医疗诊断、工业无损探伤和食品安全检测等领域广泛的应用[1-5]，其对图片质量的要求也越来越高，进而对软硬件特别是算法的要求也越来越高．在众多算法中，FDK算法[6]应用最为普遍．FDK算法是由Feldkamp、Davis和Kress提出的一种基于圆轨道扫描的近似重建算法，其本质是滤波反投影(filtered back projection，FBP)，它对图像质量的影响非常明显．传统的滤波函数能保持较高的空间分辨率，但同时引起明显的Gibbs现象(即有明显的振荡效应)，致使重建效果较差．因此，在保持高图像分辨率的情况下设计新的滤波函数，降低Gibbs现象就尤为重要．为此，研究人员相继提出NEW滤波函数[7]、R-L-S-L、R-L-NEW和R-L-MS-L等混合滤波函数[8-10]来消除Gibbs现象．虽然这些滤波函数都具有保持高空间分辨率的同时减小Gibbs现象的作用，但无法完全消除Gibbs现象，主要原因是与之结合的R-L滤波函数的近旁瓣突出，远旁瓣的幅度和宽度较大[9-10]，而NEW滤波函数和R-L滤波函数一样，由理想滤波器推导出，所以其近旁瓣也较为突出[7].本研究基于FDK算法，设计了一种新型滤波函数进行图像重建，在保持较高空间分辨率的情况下大幅减小Gibbs现象，提高了密度分辨率，进而改进了重建图像质量．

1 FDK算法介绍

FDK算法因其高效、简便以及易于图像处理器(graphics processing unit，GPU)加速，至今仍被大量使用．FDK算法本质上是FBP，把得到的锥束投影数据进行滤波，然后利用扇形束近似重建而得．FDK算法的计算公式[11]如式(1)和式(2)．

对投影数据P的加权滤波为

(1)

其中，R为光源到物体中心的距离；β为源绕中心旋转轴z轴的旋转角度；a为旋转中心的横坐标；b为旋转中心的纵坐标；P(β,a,b)为投影数据；G(a)为滤波函数；符号*表示卷积运算．

反投影重建结果为

(2)

其中，U(x,y,β)=R+xcosβ+ysinβ为加权函数，这里x和y为探测器坐标；P′(β,a,b)为加权滤波后的投影数据；其他变量定义如式(1)．

影响重建结果好坏的关键在于滤波函数的选择、重建过程中插值的方式，以及锥角的大小等．从式(2)可直观地看出，滤波函数能直接影响到反投影重建的结果．所以，合适的滤波器是实现高质量重建图像的关键因素之一．

2 新型滤波函数的构建

2.1 选择要混合和加权平均的滤波函数

要选择合适的滤波函数进行混合和加权平均，必须要先判断滤波函数的优劣特性．判断一个滤波函数对重建结果的影响主要有：主瓣、近旁瓣和远旁瓣．主瓣高而窄，说明空间分辨率好；远旁瓣的幅度和幅值越小，说明Gibbs现象越小、密度分辨率越好[12-13]．范惠荣等[14]研究表明，NEW滤波函数能够保持空间分辨率的同时减小Gibbs现象，而S-L滤波函数[11]可通过这3点加权平均使远旁瓣的幅度和幅值大幅减小，其近旁瓣收敛相比R-L[11]、S-L和NEW滤波函数更快，更能有效地抑制Gibbs现象，但因其主瓣变矮，空间分辨率会变得很差，如图1．其中，n为采样点；h[n]为采样点n所对应的滤波函数值．图2中除R-L滤波函数外，剩下3种滤波函数的远旁瓣几乎重叠，表明M3S-L滤波函数[10]的远旁瓣的幅度和幅值非常小，与R-L滤波函数相比无明显振荡，说明Gibbs现象非常小．因此，可将NEW滤波函数和加权平均后的M3S-L滤波函数混合叠加，得到新的NEW-MS-L滤波函数，大幅减小Gibbs现象，且能保持与单独使用NEW滤波函数后相当的空间分辨性能．

图1 R-L、S-L、NEW和M3S-L滤波函数的空域主瓣分布Fig.1 (Color online) Main lobe distributions in spatial domain of R-L,S-L,NEW, and M3S-L filter functions

图2 R-L、S-L、NEW和M3S-L滤波函数的远旁瓣分布Fig.2 Far lobe distributions in spatial domain of R-L, S-L, NEW, and M3S-L filter functions

2.2 构建新型滤波函数NEW-MS-L

新型滤波函数是根据加权平均和混合滤波的思想构建的．首先需将S-L滤波函数进行加权平均．

S-L滤波函数的离散形式[11]为

(3)

其中，n=0,±1,±2,…, 为采样点(后面各式含义相同)；τ为探测器单元的大小，一般设为1．

基于文献[15]的研究结果，本研究对S-L滤波函数进行3点加权平均，记为M3S-L，该函数的离散形式[10]为

hM3S-L[n]= 0.6hS-L[n]+0.2hS-L[n-1]+

0.2hS-L[n+1]

(4)

将M3S-L滤波函数和NEW滤波函数进行混合滤波，得到新的滤波函数NEW-MS-L．NEW滤波函数[7]和NEW-MS-L滤波函数的离散形式分别为

(5)

hNEW-MS-L[n]=k1×hM3S-L[n]+

k2×hNEW[n]

(6)

其中，k1和k2为权重，k1+k2=1． 本研究取k1=0.5；k2=0.5．

NEW-MS-L、NEW和M3SL滤波函数在空域的主瓣分布对比如图3．

图3 NEW、M3S-L和NEW-MS-L滤波函数的空域主瓣分布Fig.3 (Color online) Main lobe distributions in spatial domain of NEW,M3S-L, and NEW-MS-L filter functions

从图3可见，新型滤波函数的hNEW-MS-L[n]主瓣高度与NEW滤波函数的相当，近旁瓣幅度比NEW滤波函数的小，且收敛更快．远旁瓣的幅度和幅值很小，表明NEW-MS-L滤波函数可实现与NEW滤波函数相当的空间分辨率，且能更有效抑制Gibbs现象，进一步提高密度分辨率，获得更优的图像质量．

3 仿真结果与分析

基于FDK算法，分别用NEW、R-L-S-L、R-L-N、R-L-MS-L和NEW-MS-L滤波函数对尺寸为256×256×256像素的Shepp-Logan三维头模型[16]进行重建，然后观察中心面处的截面及其纵向第128行的灰度曲线图，结果如图4．

图5(a)至图5(f)分别为采用NEW、R-L-S-L、R-L-NEW、NEW-MS-L和R-L-MS-L滤波函数重建的纵向第128行的灰度曲线图．灰度曲线图的波动大小反应与原始模型的差异，波动越大说明差异大，表现为图像越粗糙．由图5可见，NEW-MS-L较其他滤波函数能够更好的还原原始模型．

图4 原始模型图像与用NEW-MS-L滤波函数的重建图像Fig.4 Original model image and reconstruction image by NEW-MS-L filter function

图5 原始模型及使用不同滤波函数重建结果的灰度曲线Fig.5 The profile pictures of original model and reconstructed results by different filter functions

仅通过灰度曲线图的对比来说明NEW-MS-L滤波函数的优越性是不够的，还需通过计算NEW、R-L-S-L、R-L-N、R-L-MS-L和NEW-MS-L滤波函数的归一化均方误差d和归一化平均绝对误差r， 如式(7)和式(8)，进行定量对比.

(7)

(8)

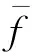
d反映少数点的大误差，d=0表示重建后图像完全再现了原始模型图像；d越小表示两者的偏差越小．r反映多数点的小误差，r=0表示重建图像与头模型原始图像无误差；r越小说明误差越小．

表1为分别采用NEW、R-L-S-L、R-L-NEW、R-L-MS-L和NEW-MS-L滤波函数重建图像后的d值和r值对比．

表1 重建结果的误差值对比

由表1可见，采用NEW-MS-L滤波函数后的d值与采用NEW滤波函数后的d值相当，且所得r值较其他滤波函数的都小，说明采用NEW-MS-L滤波函数所得的重建效果更佳．

上述结果还可通过调整k1和k2值来进一步优化[10]．d和r随k1的变化如表2，由表2可知，当k1=0.8时，d值最小；但当k1=0.7、 0.8和0.9时，d值虽然相差无几，但r值随k1的增加而变大，且变化较明显．所以，本研究权衡d和r的值，选取k1=0.7．

表2 误差值d与r随k1的变化

当k1=0.7，k2=0.3时，可得到d=0.315 5，r=0.737 3． 虽然r值增大了，但d值进一步减小．将NEW-MS-L滤波函数的d值和r值与表1的其他滤波函数的d值和r值进行对比，结果反映新滤波函数性能比其他滤波函数要好．

结 语

基于混合滤波和加权平均理论，构建新型滤波函数NEW-MS-L．其空域主瓣分布图具有主瓣高而窄、近旁瓣小、远旁瓣衰减快等特征，能很好地抑制Gibbs现象，保持较高的空间分辨率．仿真结果表明，通过对比NEW、R-L-S-L、R-L-NEW、R-L-MS-L滤波函数重建结果与灰度曲线图，并分析归一化均方误差和归一化平均绝对误差，发现NEW-MS-L滤波函数可在保持较高空间分辨率的情况下更有效地抑制Gibbs现象，密度分辨率更高，重建结果也更平滑．此外，根据实际情况适当调整k1和k2， 能使图像效果达到符合预期的要求．

NEW-MS-L滤波函数在本次仿真实验中主要针对传统基于吸收效应的CT，今后可进一步探讨NEW-MS-L滤波函数在相衬CT[17-22]中的应用．

/ References：

[1] Egan C K,Jacques S D M,Wilson M D, et al.3D chemical imaging in the laboratory by hyperspectral X-ray computed tomography[J].Scientific Reports,2015,5: 15979.

[2] Bieberle M,Barthel F.Combined phase distribution and particle velocity measurement in spout fluidized beds by ultrafast X-ray computed tomography[J].Chemical Engineering Journal,2016,285:218-227.

[3] Edlund R,Skorpil M,Lapidus G,et al.Cone-beam CT in diagnosis of scaphoid fractures[J].Skeletal Radiology,2016,45(2):197-204.

[4] Senyshyn A,Mühlbauer M J,Dolotko O,et al.Homogeneity of lithium distribution in cylinder-type Li-ion batteries[J].Scientific Reports,2015,5:18380.

[5] Plessis A D, Olawuyi B J, Boshoff W P, et al. Simple and fast porosity analysis of concrete using X-ray computed tomography[J]. Materials and Structures, 2016, 49(1): 553-562.

[6] Feldkamp L A, Davis L C, Kress J W. Practical cone-beam algorithm[J]. Journal of the Optical Society of America A, 1984, 1(6): 612-619.

[7] Wei Yuchuan, Wang Ge, Hsieh J. An intuitive discussion on the ideal ramp filter in computed tomography (I)[J]. Computers & Mathematics with Applications, 2005, 49(5/6): 731-740.

[8] 谢 强．计算机断层成像技术:原理、设计、伪像和进展[M]．张朝宗，郭志平，王宗贤，译．北京：科学出版社，2006． Hsieh J.Computed tomography: principle, design, artifacts and recent advances[M]. Zhang Chaozong,Guo Zhiping, Wang Zongxian, trans. Beijing: Science Press,2006.(in Chinese)

[9] 胡永梅，全 红，徐利明，等．新型混合滤波器在FDK算法中的应用[J]．中国医学影像技术，2011，27(2)：397-400． Hu Yongmei, Quan Hong, Xu Liming, et al. Application of a new mixed filter in FDK algorithm [J]. Chinese Journal of Medical Imaging Technology, 2011, 27(2): 397-400.(in Chinese)

[10] 王晓鹏，王明泉，侯慧玲．基于R-L-MS-L滤波函数的CT图像重建[J]．电视技术，2014，38(7)：26-28． Wang Xiaopeng,Wang Mingquan,Hou Huilin. CT image reconstruction based on R-L-MS-L filter function[J].Video Engineering, 2014,38(7): 26-28.(in Chinese)

[11] 闫 镔，李 磊．CT图像重建算法[M]．北京：科学出版社，2014． Yan Bin,Li Lei.CT image reconstructinalgorithm[M].Beijing:Science Press,2014.(in Chinese)

[12] 郑君里．信号与系统[M]．北京：高等教育出版社，2002． Zhen Junli. Signals and systems[M].Beijing:Higher Education Press,2002.(in Chinese)

[13] 杨位钦，顾 岚．时间序列分析与动态数据建模[M]．北京：北京工业学院出版社，1986． Yang Weiqin,Gu Lan. Time series analysis and dynamic data modeling [M].Beijing:Beijing Institute of Tchnology Press,1986.(in Chinese)

[14] 范惠荣，徐茂林，邱 钧，等．关于CBP算法的一种新型滤波函数和它的性质[J]．电子学报，2004，32(2)：232-235． Fan Huirong,Xu Maolin,Qiu Jun,et al. A new filter function in CBP and its properties[J].Acta Electronica Sinica,2004,32(2):232-235.(in Chinese)

[15] 刘 晓，杨朝文．RL滤波函数的改进对卷积反投影图像重建的影响[J]．四川大学学报自然科学版， 2004，41(1)：112-117． Liu Xiao,Yang Chaowen. The influence of modified-RL filter function on the quality of image reconstruction using convolution backprojection algorithm [J].Journal of Sichuan University Natural Science Edition,2004,41(1):112-117.(in Chinese)

[16] 刘 泽，孙丰荣，李艳玲，等．基于3D Shepp-Logan头部模型的三维医学图像重建仿真[J]．生物医学工程学杂志，2006，23(5)：938-943． Liu Ze,Sun Fengrong,Li Yanling, et al.The three-dimension medical image reconstruction simulation on 3D Shepp-Logan head phantom [J].Journal of Biomedical Engineering,2006,23(5):938-943.(in Chinese)

[17] Lei Yaohu,Huang Jianheng,Liu Xin,et al.Improvement of visibility of moir fringe in X-ray differential phase-contrast imaging[J].Journal of Shenzhen University Science and Engineering,2016, 33(5):506-510.

[18] 刘 鑫，郭金川．部分相干光源微分相衬双图像相位恢复[J]．深圳大学学报理工版，2014，31(2)：169-173． Liu Xin,Guo Jinchuan.Dual-images phase retrieval in differential phase-contrast imaging with partial coherence source[J].Journal of Shenzhen University Science and Engineering,2014,31(2):169-173.(in Chinese)

[19] Jerjen I, Revol V, Kottler C, et al. Phase contrast cone beam tomography with an X-ray grating interferometer [C]// International Conference on Advanced Phase Measurement Methods in Optics & Imaging.Ascona, Switzerland: American Institute of Physics, 2010, 1236(1):227-231.

[20] Huang Zhifeng, Kang Kejun, Li Zheng, et al. Direct computed tomographic reconstruction for directional-derivative projections of computed tomography of diffraction enhanced imaging[J]. Applied Physics Letters, 2006, 89(4): 041124.

[21] McCann M T, Nilchian M, Stampanoni M, et al. Fast 3D reconstruction method for differential phase contrast X-ray CT[J]. Optics Express, 2016, 24(13): 14564-14581.

[22] Fu Jian, Hu Xinhua, Velroyen A, et al. 3D algebraic iterative reconstruction for cone-beam X-ray differential phase-contrast computed tomography[J]. PloS One, 2015, 10(3): e0117502.

【中文责编：英 子；英文责编：木 南】

2016-11-29；Accepted：2017-03-09

Professor Guo Jinchuan. E-mail: jcguo@szu.edu.cn

A new filter function for the image reconstruction of cone beam X-ray CT

Hong Zhenhou, Zhou Bin, and Guo Jinchuan

College of Optoelectronic Engineering, Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China

The conventional filter function of the FDK algorithm in X-ray computed tomography (CT) can result in the obvious Gibbs phenomenon, which has great effect on the CT image. A NEW-MS-L filter function is deduced based on the rationale of mixed filter theory and weighted average theory. First, the S-L filter function is weighted and averaged to form M3S-L filter function.Then, as a superposition of the M3S-L filter function and the NEW filter function, the NEW-MS-L filter function is obtained. Compared with the other filter functions such as NEW, R-L-S-L, R-L-NEW, and R-L-MS-L, the NEW-MS-L can suppress the Gibbs phenomenon while maintaining high resolution. The results show that the NEW-MS-L filter function can provide X-ray CT with better reconstruction images.

optical engineering; computed tomography; FDK algorithm; filter function; Gibbs phenomenon; mixed filter theorem; weighted average theorem

：Hong Zhenhou,Zhou Bin,Guo Jinchuan.A new filter function for the image reconstruction of cone beam X-ray CT [J]. Journal of Shenzhen University Science and Engineering, 2017, 34(3): 284-289.(in Chinese)

国家自然科学基金资助项目(11674232，11074172)

洪振厚(1991—)，男，深圳大学硕士研究生．研究方向：X光成像．E-mail：paul_hongzh@163.com

TP 391.41

A

10.3724/SP.J.1249.2017.03284

Foundation：National Natural Science Foundation of China(11674232, 11074172)

引 文：洪振厚，周 彬，郭金川．锥束X射线CT图像重建的新型滤波函数[J]. 深圳大学学报理工版，2017，34(3)：284-289.