数控机床工作台误差综合补偿方法研究

苗恩铭 徐建国 吕玄玄 魏新园

合肥工业大学仪器科学与光电工程学院，合肥，230009



数控机床工作台误差综合补偿方法研究

苗恩铭 徐建国 吕玄玄 魏新园

合肥工业大学仪器科学与光电工程学院，合肥，230009

针对由几何误差与热误差引起的数控机床工作台与主轴之间相对位置变动的问题，通过试验分析其在不同温度状态下的误差数据，得到机床工作台平面度误差随热变形保持不变的规律，并提出了一种数控机床工作台平面度误差与主轴热误差的综合补偿方法。该方法通过分别建立工作台平面度误差模型和热误差模型，并运用叠加原理建立综合误差补偿模型，对传统固定单位置点建模补偿方法的原理性缺陷进行了改进。结合机床关键部件的实时温度值和刀具位置的实时坐标值，计算出了全工作台各区域各温度阶段的误差补偿值，进而实现了全工作台主轴轴向综合误差的实时补偿。检验及分析结果表明，相比于传统固定单位置点热误差建模补偿方法，该方法所建模型残余标准差减小约7 μm，精度提高比例达到50%；单次最大补偿残差减小约11 μm，精度提高比例达到60%，大幅度提高了机床的加工精度。

数控机床工作台；平面度误差模型；热误差模型；综合模型

0 引言

在精密数控机床加工过程中，工作台作为数控机床装夹工件的载体，它与机床刀具的相对位置直接决定机床的加工精度。数控机床加工过程中，机床部件不均衡温升产生的热误差、零件本身及组装过程产生的几何误差，都会使得刀具与工作台之间的相对位置变化[1]。这些变化最终转化为零件的加工误差。据统计，在精密及超精密加工中，由几何及热引起的误差占总误差的70%左右[2-3]，所以研究机床全工作台主轴轴向误差综合补偿技术意义重大。

针对上述情况，科研人员通常利用软件补偿技术对数控机床误差进行在线补偿[4]。在机床热误差领域，科研人员一般按照国际标准《机床检验通则第3部分：热效应测定》(ISO 230-3:2007)的规定，由机床主轴与工作台特定单位置点的热变形来表征数控机床的热特性，通过建立固定单点与关键热源温度之间的补偿模型，结合基于原点偏移的热误差补偿系统给予提前补偿，以提高机床的加工精度[5-6]。针对机床几何误差，大多通过提高机床组成部件的精度提前实现误差防止[7]，或者利用单独的几何误差建模和由数控系统提供的参数设定方式的误差补偿功能(如螺距补偿、刀具补偿等)实现几何误差的补偿[8]。

然而，在实际加工中，由于被加工工件对工作台的挤压，机床X轴、Y轴在制造过程中的不完全水平以及丝杠导轨的受热变形等，会产生复杂的几何误差和热误差，所以，采用传统的固定单点位置热误差建模的补偿方法，只能解决机床部分热误差的影响，而单独的几何误差补偿方法也无法完全避免热误差的影响，导致这些方法存在一定的应用缺陷。对此，王维等[9]采用定位误差和热误差综合建模的方法抑制机床定位误差随机床热变形的影响。

为了弥补传统固定单位置点建模补偿方法的不足，本文提出一种数控机床工作台几何误差和热误差综合补偿方法。该方法与传统工作台上固定单位置点建模补偿方法预测精度对比结果验证了本文方法的有效性。

1 机床全工作台综合误差测量试验

1.1 试验方案设计

由ISO 230-1-2012《机床检验通则 第1部分：在无负荷或精加工条件下机床的几何精度》标准可知，机床平面度误差分为机床工作台平面度误差和沿两线性轴运动而产生虚拟平面的平面度误差。在实际加工中，工件直接固定在机床工作台上，工作台沿两线性轴X轴、Y轴运动，由刀具垂直下方对应工作台点构成的虚拟平面的平面度为上述两种平面度的叠加。故本文针对以上两种平面度误差，改进国际标准中关于平面度误差测量方案，采用坐标采集系统由主轴直接测量出的工作台面内不同点的空间位置坐标，拟合工作台曲面，作为平面度评定标准。

按照ISO 230-3-2007《机床检验通则 第3部分：热效应的确定》标准对机床热误差的规定，本试验采用空转方式运行。试验过程中，主轴以恒定转速6000 r/min转动，工作台沿X轴、Y轴以400 mm/min的进给速度往返运行，每运行5 min采集温度和热变形量一次。试验持续4 h以上。试验分三批次进行，第一批次为建模试验，第二、第三批次为验证试验。每批次试验相隔一天，机床充分冷却至环境温度状态，以保证试验的验证效果。三批次试验环境温度变化范围分别为19.56～26.88 ℃、21.19～27.94 ℃和21.56～26.88 ℃。

1.2 试验装置

本文以典型的C型数控机床Leaderway-V450立式加工中心为研究对象，其工作台的尺寸为620 cm×350 cm。根据工作台尺寸，提出了在工作台上设置15点位置测量方案，具体测点(工作台上数字1～15为15个测点的编号)分布位置如图1所示。试验所采用的测量系统分为温度采集系统和坐标采集系统[10]，温度采集系统选用温度传感器DS18B20(测量精度为±0.2 ℃，最高分辨力为0.0625 ℃)来测量温度数据。其中，温度传感器的贴放位置以影响机床主轴三向热误差的主要热源附近为主，温度传感器(T1～T20为温度传感器编号(T10未在图中标出))的安放位置如图1和表1所示[11]；坐标采集系统是由在线检测系统(本试验所使用的在线检测系统为哈尔滨先锋机电有限公司生产的OP550型在线检测系统)、机床外扩I/O单元、坐标采集卡和计算机组成。其原理是：在线检测系统测量测头当前所在位置坐标，通过机床外扩I/O单元将此坐标值输出到坐标采集卡中，并利用坐标采集卡将坐标值输入计算机，最终完成坐标采集。同一温度时刻，工作台不同测点坐标值拟合出的曲面为该温度平面度评定标准，而不同温度时刻，各测点的坐标值偏差为该点Z轴热误差数据。

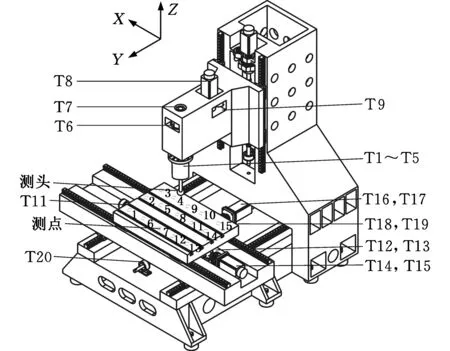
图1 温度传感器及测点分布示意图Fig.1 The distribution diagram of temperature sensors and measuring points

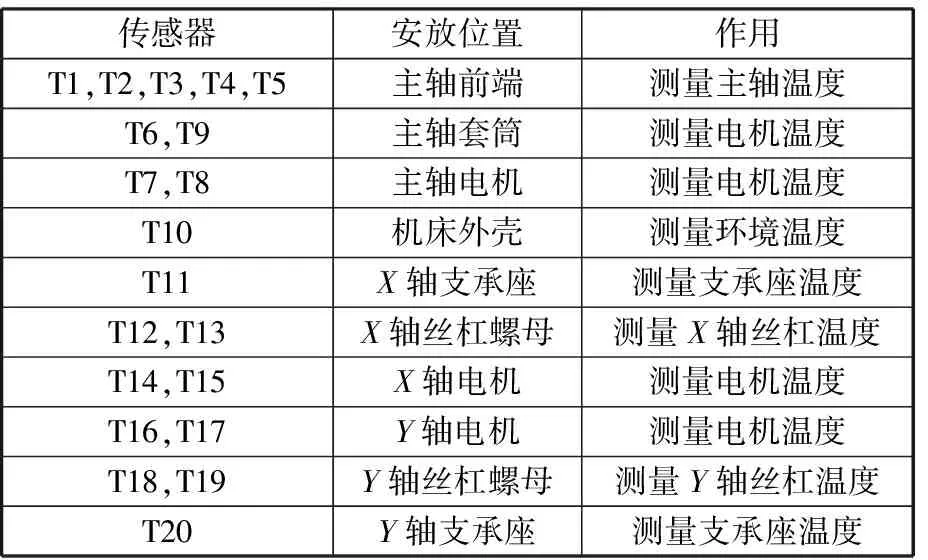
表1 传感器安放位置及作用

测量试验数据时，温度数据和热误差数据为同步测量。试验装置实物如图2所示。

图2 温度采集系统和坐标采集系统实物图Fig.2 The practicality picture of temperature measurement system and coordinate collection system

2 机床综合误差补偿方案确定

2.1 工作台Z轴轴向变形特征分析

根据第一批试验采集的温度信息，绘制温升趋势图。为能清楚地表示出温度变化过程，现在从20个温度传感器中选取T1～T10号10个传感器测量的温度绘图，温升趋势如图3所示，其中，竖虚线为所截取的测量时刻。选取温升过程中温度值变化较大的三个时刻，即第0 min、第30 min和第180 min时刻，根据此三个时刻所对应的工作台上15点位置对应的坐标值，由MATLAB的surf函数和三次样条插值法[12-13]，画出工作台面形态图，如图4所示。

图3 温升趋势图Fig.3 The trend of temperature change

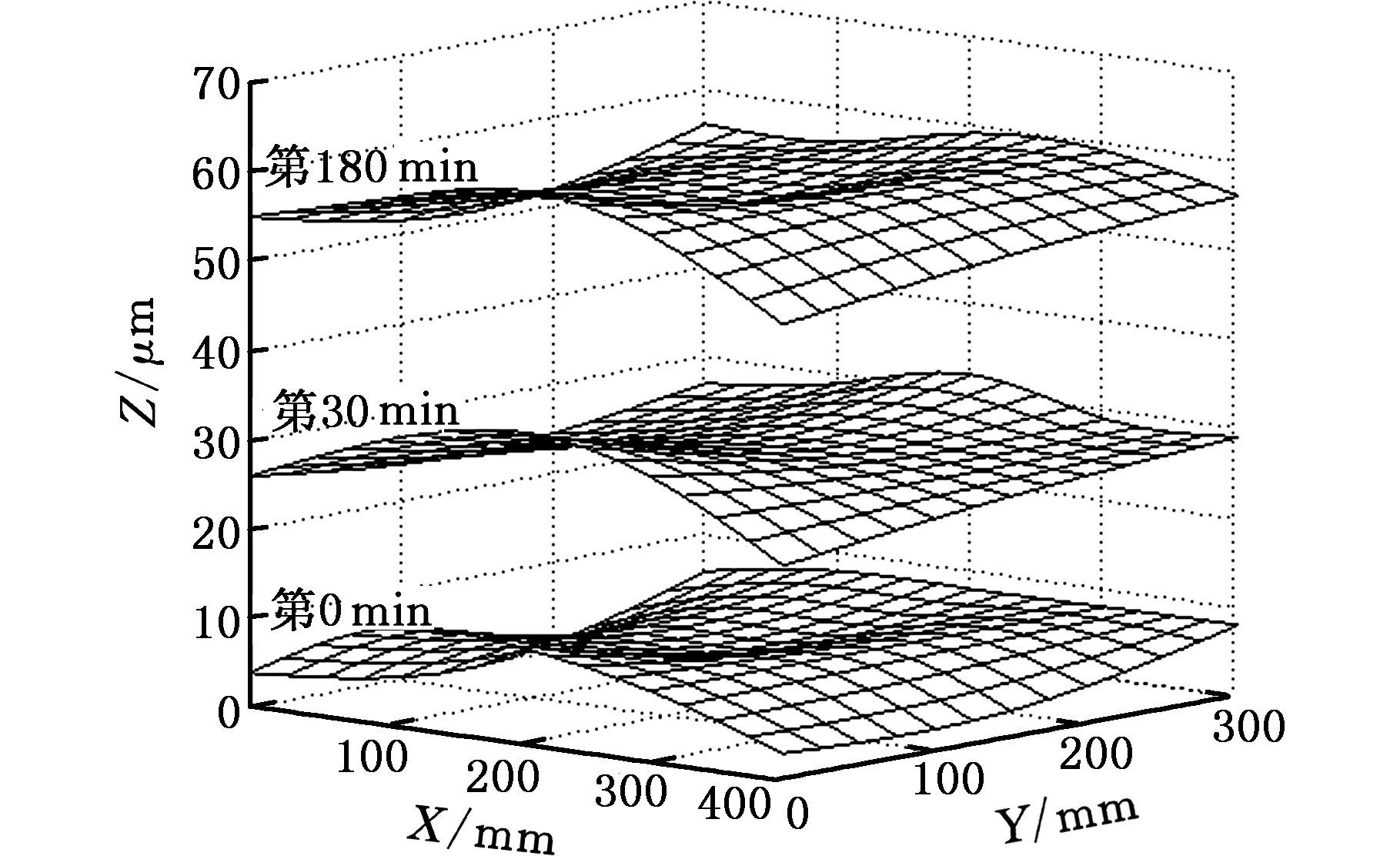
图4 工作台面第0 min、30 min、180 min形态图Fig.4 The diagram of worktable’s plane shape on the 0 th,30 th and 180 th min

由图4可知，工作台存在初始平面度误差，即工作台各点初始坐标存在差异。随着温度的升高，工作台沿主轴Z向呈整体上升趋势，且随着温度的变化，形状没有较大改变，即各点之间的坐标值差异依然基本保持不变。

从所测数据中提取各测点的Z向坐标，减去工作台的初始平面度误差后，计算相应的热变形量，得到各测点处Z轴热变形量的趋势图，如图5所示。

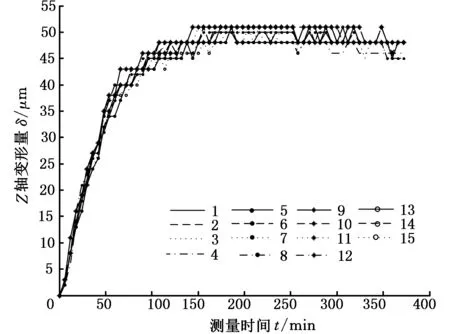
图5 第一批试验工作台15点Z轴的热变形趋势Fig.5 The trend of thermal deformation of the 15 points’ Z-axis in the first experiments

分析图5可知，在试验中，工作台各位置点均沿机床Z轴轴向发生热变形，规律性明显。同一测量时刻工作台上的各测点的主轴Z向热变形量相差在5 μm之内，即减去工作台初始平面度误差后，各测点之间的相对热误差变化不大。

2.2 工作台Z轴轴向综合误差补偿方案确定

工作台各测点均沿Z轴轴向发生热变形，并且工作台平面度误差基本保持不变，故本文针对热误差和工作台平面度误差采用独立建模的补偿方法。先对工作台初始面的形状进行拟合建模，建立工作台的初始平面度误差模型f(x,y)，该模型根据X、Y任意坐标求出其所在位置平面度误差；再根据工作台各测点Z轴轴向热误差变化规律，建立15个测点的热误差模型zj(j=1,2,…,15)，并选择最优的热误差模型zj；然后将所选热误差模型与工作台初始平面度误差模型叠加，构建一个全工作台Z轴轴向综合误差补偿的模型：

z=f(x,y)+zj

(1)

式中，z为全工作台Z轴轴向综合误差补偿值。

3 综合误差模型建模过程

3.1 热误差模型的建立

多元线性回归模型是机床热误差模型的常用建模方法，它是以温度值增量为自变量，热变形量为因变量进行建模的[14]。在建模过程中，常使用模糊聚类和灰色关联度相结合的方法，筛选出温度敏感点作为变量，在保证所建模型精度的同时，降低过多温度变量带来共线性误差的影响[11]。本文按照文献[11]的温度敏感点筛选方法，选定温度传感器T1和T8作为温度敏感点进行建模。假设试验时工作台每点位置测量次数为n，则其通用表达式为

zj=b0+b1Δθ1i+b2Δθ8i+ei

(2)

i=1,2,…,n

式中，Δθ1i、Δθ8i分别为T1和T8温度敏感点处的第i次测量时刻温度值增量;b0为常数项；b1为温度敏感点T1的回归系数估计值；b2为温度敏感点T8的回归系数估计值；zj为j点热变形测量值;ei为理论值与实际测量值zj之间存在的偏差，也称残差。

现根据式(2)，针对第一批试验全工作台15点测量数据进行多元线性回归建模，得到各模型系数和标准差如表2所示。

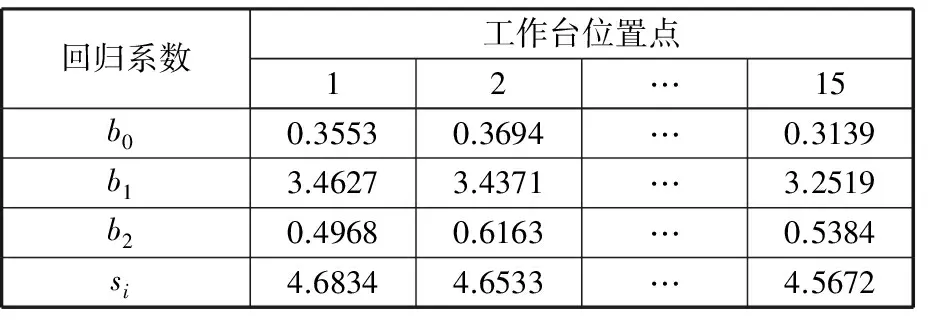
表2 工作台15处回归模型参数

表2中，si分别为工作台15个位置点所建热误差模型的拟合标准差，i=1,2,…,15。

3.2 热误差模型的选取

根据Z轴轴向误差综合补偿建模的要求，本文需要在15处热误差模型中选取一个最佳模型参与综合建模。本文通过各测点的热误差模型的预测精度来选择最优热变形建模位置点。将15处模型分别对第二批次和第三批次试验数据进行预测，得出预测标准差如表3所示。

通过对表3中的标准差进行进一步分析，将每一个模型的45个预测精度参数给予平均化和离散化，分别得到每一个模型的预测精度平均值参数Mn和预测精度离散标准差参数Sd。Mn越小，表示模型平均预测精度越高，Sd越小，表明模型的预测稳健性越强。第一批次15处模型预测精度参数Mn和Sd结果如表4所示。将表4中数据以折线图的方式表示，如图6所示。

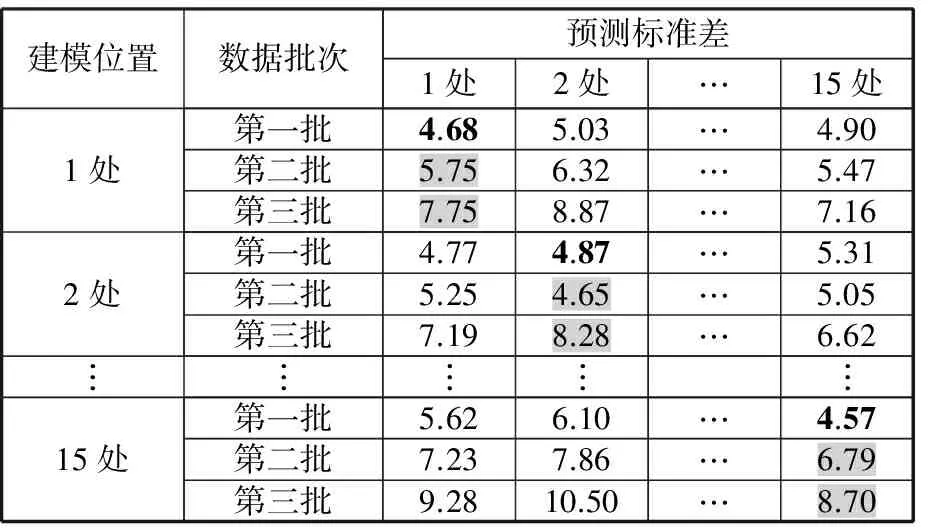
表3 第一批次15处模型的预测标准差

注：表中加粗部分为工作台各位置点处对自身的多元线性回归拟合的标准差；灰色部分为对同位置其他批次的预测标准差。

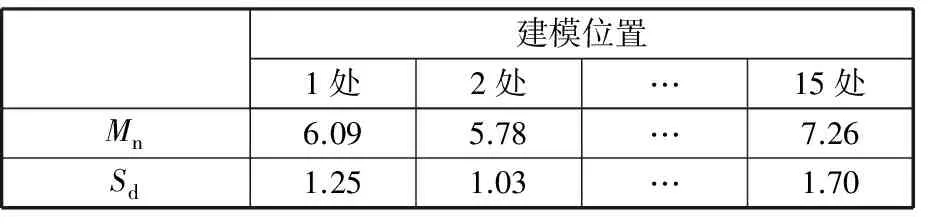
表4 第一批次15处模型预测精度的标准差和平均值

图6 第一批次15处模型预测精度趋势图Fig.6 The trend of forecast accuracy of the 15 models in the first batch

由图6可得，工作台上2、5、8、11、14位置点的热误差模型预测精度相对于相邻点位置模型的预测精度要高，并且第8位置点的模型预测精度达到最高。

经分析得出原因：本文试验所选取的机床为典型的C型数控机床，机床X轴方向的整体结构基本呈对称布局，其热变形随温升变化较小；相对来说，Y轴的非对称结构导致其热变形较大。第8位置点为工作台中心点，其所处空间位置为机床的X轴、Y轴中心线对称处，同时抵消了X轴、Y轴热变形导致工作台倾斜等影响，热变形比较稳定，所以本文最终选取第8位置点所建热误差模型参与综合误差补偿建模。

选取表2中所示的工作台第8位置点处参数的热误差模型如下：

z8=0.3846+3.5321Δθ1i+0.5605Δθ8i+ei

(3)

i=1,2,…,ns8=4.7669

式中，Δθ1i为T1温度敏感点第i测量时刻相对于第0测量时刻的温度增量值；Δθ8i为T8温度敏感点第i测量时刻相对于第0测量时刻的温度增量值；z8为工作台中心位置点第8点热变形测量值；s8为第8点的拟合标准差。

3.3 全工作台平面度误差模型的建立

本文采用最小二乘曲面拟合算法拟合工作台初始曲面方程。为使补偿模型运算简单且能反映工作台平面的特性，本文选择用二元三次多项式的模型进行建模[15]：

f(x,y)=a0+a1x+a2y+a3x2+a4xy+a5y2+

a6x3+a7x2y+a8xy2+a9y3

(4)

式中，a0,a1,…,a15为相应变量的系数估计值；x为机床加工工件时X轴坐标值；y为机床加工工件时Y轴坐标值；f(x,y)为主轴在工作台上坐标为(x,y)时机床Z轴的热误差补偿值。

对平面进行最小二乘曲面拟合时，由测量的工作台初始平面坐标值确定曲面常数。试验所测工作台15点位置坐标为(0，0，4)、(0，150，0)、(0，300，6)、(100，300，8)、(100，150，6)、(100，0，11)、(200，0，11)、(200，150，6)、(200，300，8)、(300，300，8)、(300，150，8)、(300，0，8)、(400，0，3)、(400，150，3)、(400，300，8)。依据式(4)拟合的热误差曲面模型如下：

f(x,y)=4.1404+(905.26x-3.0298x2-0.7446xy-

3.6799y2+0.0017x3+0.0055x2y-0.0039xy2+

0.0129y3)×10-4

(5)

3.4 建立综合误差补偿模型

根据式(1)，由以上计算的工作台中心位置点处所建热误差模型(式(3))和工作台平面度误差模型(式(5))合并成全工作台Z轴轴向综合误差补偿模型如下：

f(x,y,θ1,θ8)=4.525+3.5321Δθ1i+0.5605Δθ8i+

(905.26x-3.0298x2-0.7446xy-3.6799y2+

0.0017x3+0.0055x2y-0.0039xy2+

0.0129y3)×10-4

(6)

4 综合误差补偿模型实施及预测精度分析

4.1 综合误差补偿原理

数控机床工作台Z轴轴向综合误差建模补偿实施是依据数控机床外部坐标原点偏移功能实现的。外部坐标原点偏移[16]是指在数控机床加工程序段执行之前或者执行过程中，改变机床零点和参考位置的相对距离，从而改变后续加工程序中的机床坐标系，使工件和刀具的相对位置发生变化，实现误差补偿功能。

Leaderway-V450数控加工中心工作台Z轴轴向误差补偿的实施是将综合补偿模型嵌入到补偿器中，然后将由温度传感器采集的温度敏感点温度值和由坐标采集系统采集的机床刀具坐标值一并输入到补偿器中，参与误差模型计算，计算出该温度时刻该坐标位置下Z轴轴向误差。再通过补偿器与机床数控系统之间的通信，将所计算的补偿值输入机床，修改PMC程序实现外部坐标原点偏移功能，达到误差补偿的目的。误差补偿原理如图7所示。

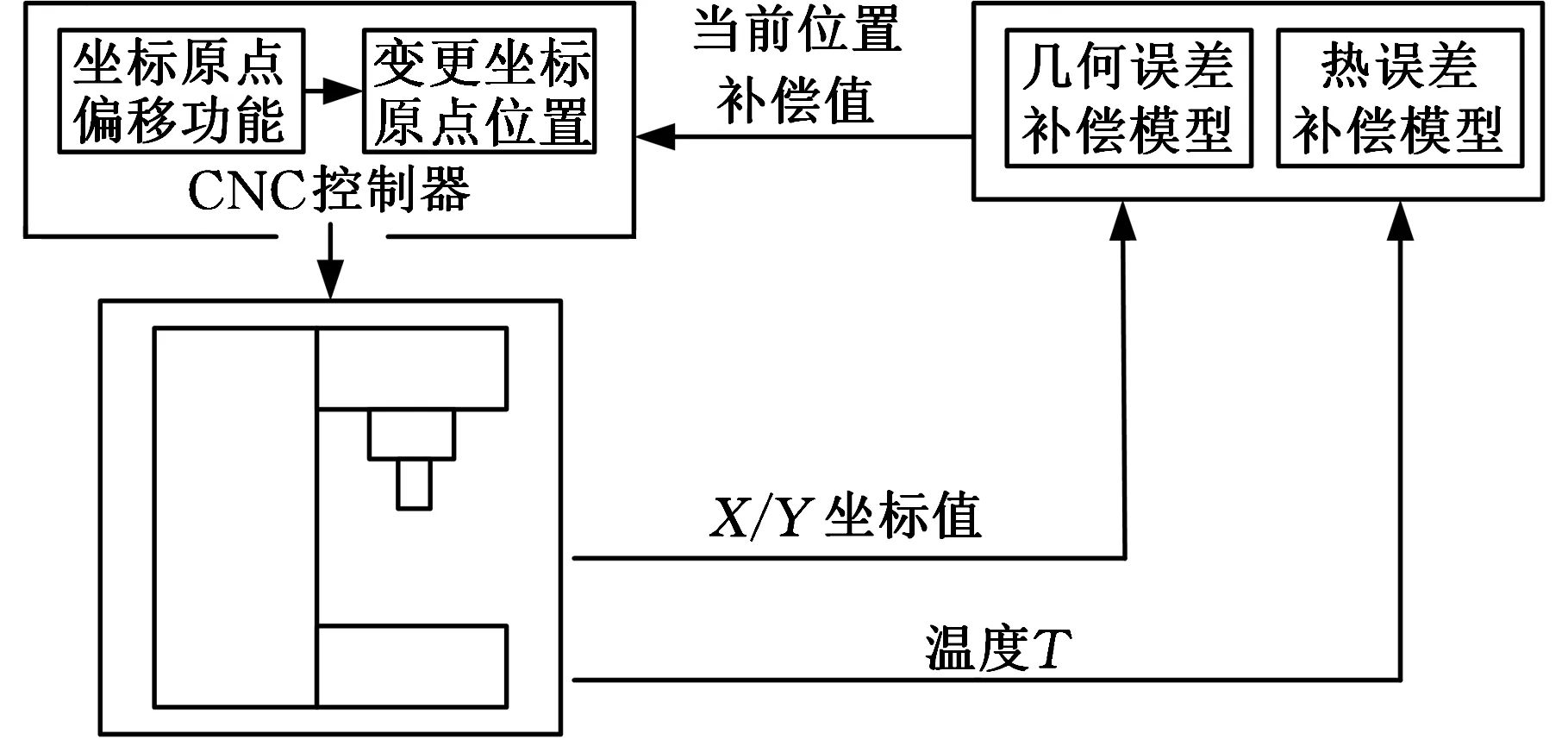
图7 误差补偿原理示意图Fig.7 Schematic diagram of error compensation principle

4.2 模型补偿精度分析

4.2.1 全工作台综合误差模型预测精度分析

上述机床全工作台综合误差模型对第二、第三批试验全工作台各温度时刻进行预测分析，得出预测的残余标准差和最大残差,如表5所示。

分析表5可知，预测第二批试验数据时，综合模型对工作台各个温度时刻预测残余标准差分布范围为1.39～10.33 μm，最大残差分布范围为2.37～12.06 μm；预测第三批试验数据时，预测残余标准差分布范围为1.36～9.81 μm，最大残差分布范围为2.65～12.45 μm。

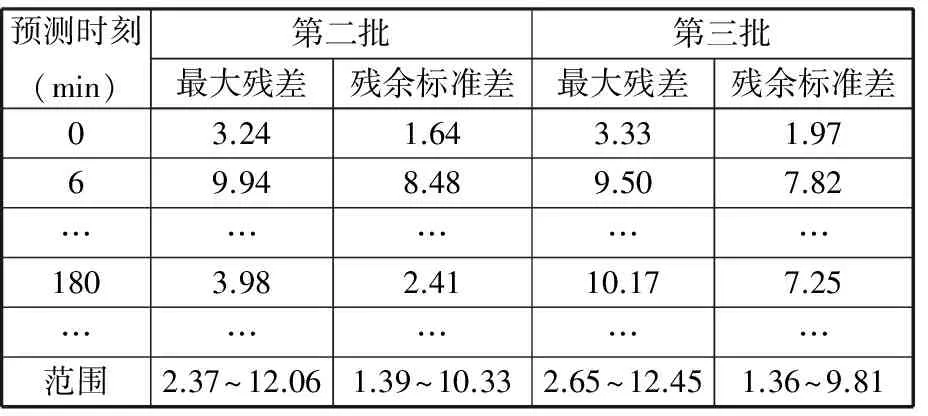
表5 综合模型对全工作台每个测量时刻预测的最大残差和残余标准差

4.2.2 传统工作台固定单位置点模型预测精度分析

按照传统工作台固定单位置点热误差建模补偿的方法，根据3.2节，以工作台最优建模位置点第8点为例，同样选定温度传感器T1和T8作为温度敏感点，所建立热误差补偿模型如式(3)所示。对第二、第三批试验数据进行预测分析，得出预测残余标准差和最大残差如表6所示。

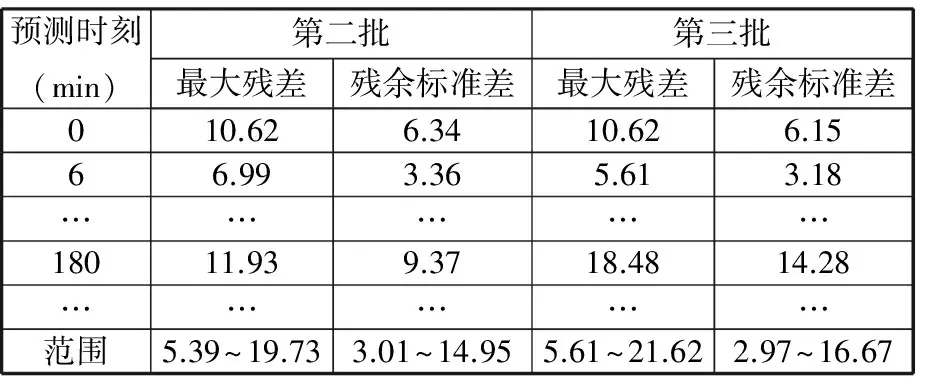
表6 单位置点热误差模型对全工作台每个测量时刻预测的最大残差和残余标准差

分析表6知，预测第二批试验数据时，传统单位置点热误差模型对工作台各个温度时刻预测残余标准差分布范围为3.01～14.95 μm，最大残差分布范围为5.39～19.73 μm；预测第三批试验数据时，预测标准差分布范围为2.97～16.67 μm，最大残差分布范围为5.61～21.62 μm。

4.2.3 预测精度对比分析

将表5、表6各批次试验按照不同建模方法预测结果绘制曲线图，见图8、图9。图8和图9中Acc为各模型对工作台各个温度时刻的预测残余标准差；Err为对工作台各个温度时刻的预测最大残差。

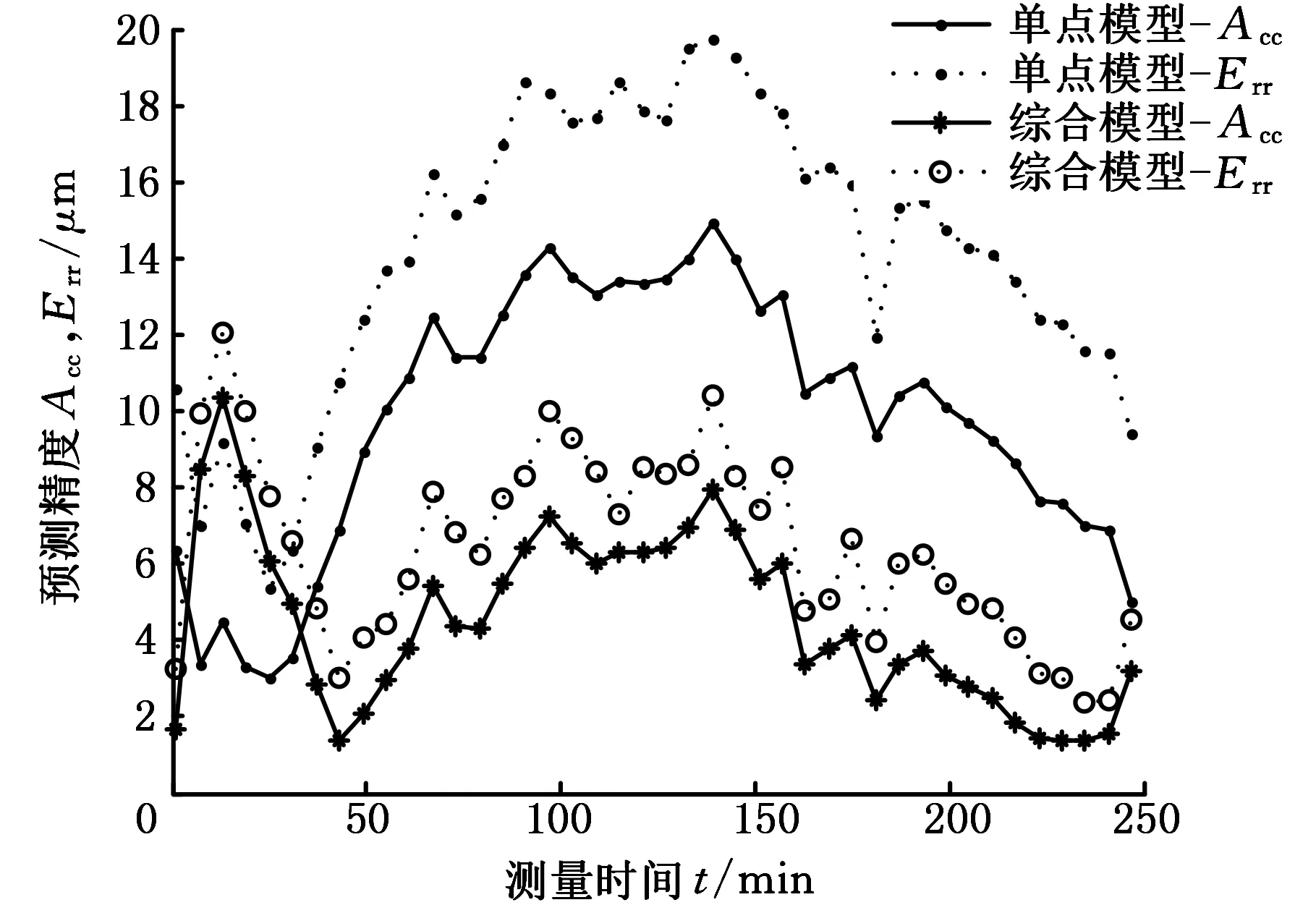
图8 对第二批次试验数据的预测效果图Fig.8 Forecasting effect analysis of the second experiments

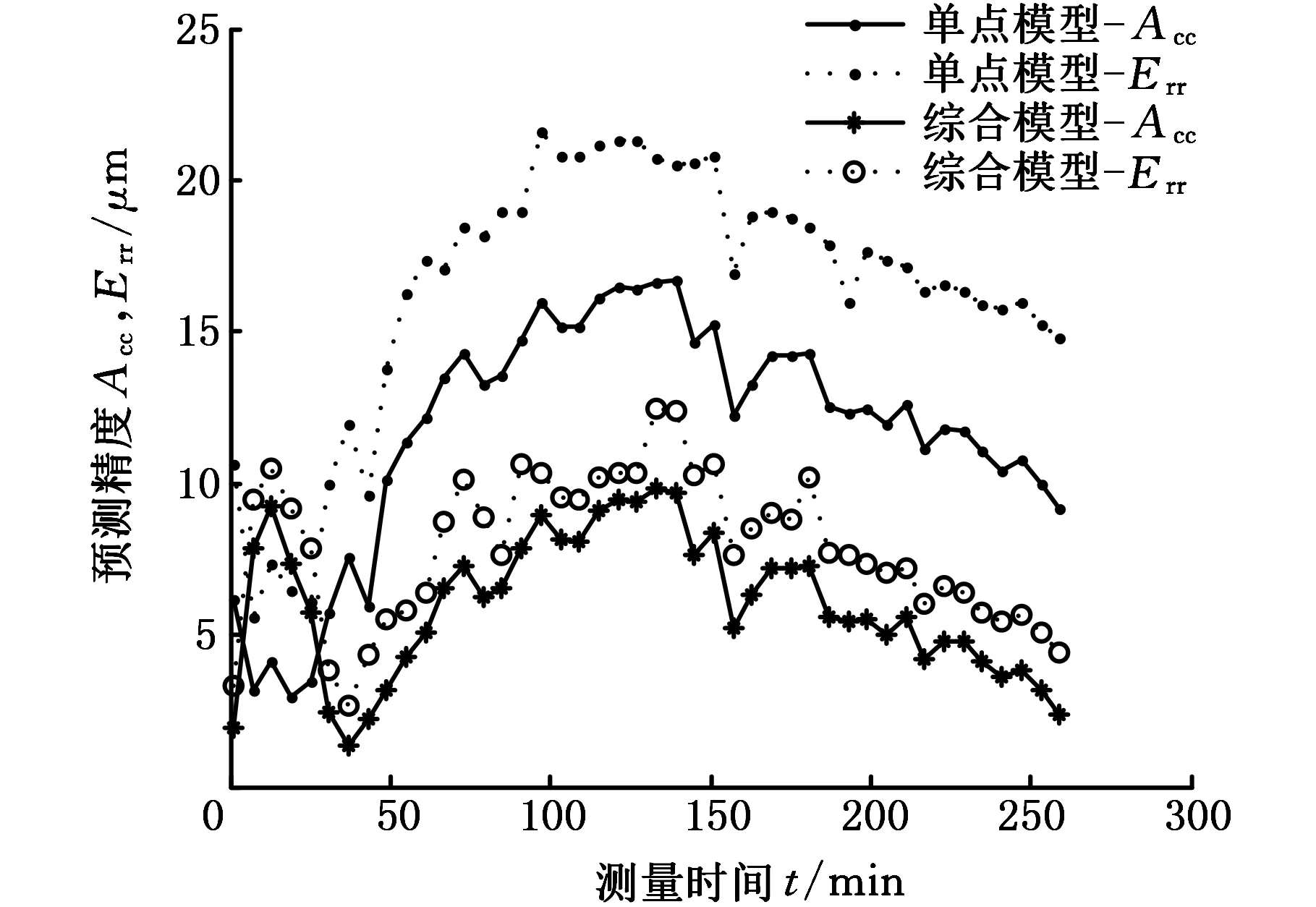
图9 对第三批次试验数据的预测效果图Fig.9 Forecasting effect analysis of the third experiments

分析图8、图9，综合模型对工作台各个温度时刻的预测残余标准差和最大残差均低于传统单位置点热误差模型的预测残余标准差和最大残差。对第二批次试验数据预测时，综合建模预测残余标准差比传统单位置点建模预测残余标准差最大减小了7.14 μm，最大残差最大减小11.31 μm。同时对第三批试验数据预测时，预测残余标准差最大减小了7.09 μm，最大残差最大减小11.30 μm。

故本文提出的Z轴轴向综合误差模型对整个工作台误差预测效果优于根据工作台单位置点测量数据建立的热误差模型对工作台误差预测效果，预测残余标准差减小了约7 μm，补偿效果提升了50%；最大残差减小约11 μm，补偿效果提升了60%。

5 结论

(1)根据对Leaderway-V450型数控机床空转热误差数据的分析，发现工作台的形状随温升基本保持不变，相对位置呈现出整体上升趋势。为同时完成对机床工作台平面度误差和主轴热误差的补偿，本文提出工作台平面度误差模型与热误差模型相加的综合误差补偿方法。

(2)建立了工作台各位置点热误差模型，并确定工作台中心位置点为最优热误差建模位置点，结合工作台平面度误差模型，建立了全工作台的综合误差补偿模型。将综合补偿模型内嵌至补偿卡中，实现了机床全工作台综合误差的实时补偿。预测效果分析显示，本文方法的补偿效果好于工作台上固定单位置点的热误差补偿效果，预测残余标准差减小约7 μm。

(3)本文对Leaderway-V450型数控加工中心的工作台进行研究，将工作台平面度误差因素引入误差补偿模型，并根据热变形过程中工作台平面度基本保持不变的性质简化了全工作台误差模型，引入坐标变量。通过补偿卡实时地对工作台各位置点进行误差补偿，为数控机床误差补偿提供了一种新的解决思路。

[1] BRYAN J B.International Status of Thermal Error Research[J]. Ann. CIRP，1990，39(2)：645-656.

[2] ARONSON R B.War Against Thermal Expansion[J]. Manuf. Eng.，1996，116(6)：45-50.

[3] YANG S，YUAN J，NI J .Accuracy Enhancement of a Horizontal Machining Center by Real-time Error Compensation[J]. Journal of Manufacturing Systems，1996，15(2)：113-124.

[4] MIAO Enming，GONG Yayun，NIU Pengcheng，et al.Robustness of Thermal Error Compensation Modeling Models of CNC Machine Tools[J]. International Journal of Manufacturing Technology，2013，69(9)：2593-2603.

[5] 张成新， 高峰，李艳.基于实时反馈的机床热误差在线补偿模型[J].中国机械工程， 2015,26(3):361-365. ZHANG Chengxin， GAO Feng， LI Yan. On-line Compensation Model Based on Real-time Feedback Thermal Errors of Machine Tools[J]. China Mechanical Engineering，2015，26(3)：361-365.

[6] 苗恩铭，刘义，杨思炫，等.无偏估计拆分算法在数控加工中心主轴热误差建模中的应用[J] .中国机械工程，2016，27(16)：2131-2136. MIAO Enming， LIU Yi， YANG Sixuan， et al. Applications of Split Unbiased Estimation Algorithm in Thermal Error Modeling of CNC Machining Center[J]. China Mechanical Engineering，2016，27(16)：2131-2136.

[7] 马军旭，赵万华，张根保.国产数控机床精度保持性分析及研究现状[J] .中国机械工程，2015，26(22)：3108-3115. MA Junxu， ZHAO Wanhua， ZHANG Genbao. Research Status and Analyses on Accuracy Retentivity of Domestic CNC Machine Tools[J]. China Mechanical Engineering，2015，26(22)：3108-3115.

[8] 刘焕牢，李曦，李斌，等.数控机床几何误差和误差补偿关键技术[J].机械工程师，2003(1)：16-18. LIU Huanglao， LI Xi， LI Bin， et al. Measurement Methods and Key Technology of CNC Machine Tool Error Compensation[J]. Mechanical Engineer，2003(1)：16-18.

[9] 王维，杨建国，姚晓栋，等.数控机床几何误差与热误差综合建模及其实时补偿[J].机械工程学报，2012，48(7)：165-170. WANG Wei， YANG Jianguo， YAO Xiaodong， et al. Synthesis Modeling and Real-time Compensation of Geometric Error and Thermal Error for CNC Machine Tools[J]. Journal of Mechanical Engineering，2012，48(7)：165-170.

[10] 苗恩铭，党连春,庄鑫栋,等.数控机床实切状态下热误差自动测量系统及其测量方法：中国，201510442587.6[P]. 2015-10-28. MIAO Enming，DANG Lianchun，ZHUANG Xindong，et al．Automatic Measurement System and Method for Thermal Error of CNC Machine Tool in Real Cutting State：China，201510442587.6[P]．2015-10-28．

[11] MIAO Eenming， GONG Yayun， DANG Lianchun， et al. Temperature-sensitive Point Selection of Thermal Error Model of CNC Machining Center[J]. International Journal of Advanced Manufacturing Technology，2014，74(5/8)：681-691.

[12] 罗尧治，公晓莺.基于双三次B样条插值的空间结构自由曲面[J].空间结构，2004，10(2)：30-34. LUO Yaozhi， GONG Xiaoying. An Algorithm Based on Bicubic B-spline Surface Interpolation for Free Surface Design[J]. Spatial Structures，2004，10(2)：30-34.

[13] 那日萨.三次B样条插值曲面及其实现[J]. 小型微型计算机系统，1995，16(3)：23-28. NA Risa. Cubic B-spline Interpolation Surface and Its Realization[J]. Mini-micro Systems，1995，16(3)：23-28.

[14] 王惠文，孟洁.多元线性回归的预测建模方法[J].北京航空航天大学学报，2007，33(4)：500-504. WANG Huiwen， MENG Jie. Predictive Modeling on Multivariate Linear Regression [J]. Journal of Beijing University of Aeronautics and Astronautics，2007，33(4)：500-504.

[15] 李二涛，张国煊，曾虹.基于最小二乘的曲面拟合算法研究[J].杭州电子科技大学学报，2009，29(2):48-51. LI Ertao， ZHANG Guoxuan， ZENG Hong. Algorithm of Surface Fitting Research Based on Least-squares Methods[J]. Journal of Hangzhou Dianzi University，2009，29(2):48-51.

[16] 姜辉，孙翰英，范嘉桢，等.基于FANUC 0i系统外部坐标原点偏移功能的数控机床误差补偿研究[J].机械制造，2009，47(7)：73-76. JIANG Hui， SUN Hanying， FAN Jiazhen， et al. Research on Error Compensation of CNC Machine Tool Based on Excursion Function of External Coordinate Origin Point of FANUC 0i System[J]. Machinery，2009，47(7)：73-76.

(编辑 王艳丽)

Study on Combined Error Compensation Method for CNC Machine Worktables

MIAO Enming XU Jianguo LYU Xuanxuan WEI Xinyuan

School of Instrument Science and Opto-electronics Engineering, Hefei University of Technology, Hefei,230009

To avoid of the relative position problems changing between the worktable and the main spindle of any CNC machine because of geometric errors and thermal errors. The error data at different temperatures were obtained through experiments, the rules of the flatness errors on worktables were obtained remaining unchanged with the thermal deformation, and a kind of comprehensive compensation method of the flatness error and thermal error on worktables of CNC machine tool was proposed. In this method, the flatness error model and thermal error model were established separately, then the comprehensive error compensation model was established by using the superposition principle. The principle’s defects of the traditional fixed point model compensation method were corrected. Based on the real-time temperature values of the key parts of CNC machine and the real-time coordinate values of the tool positions, the error compensation values of each stage of the whole working table were calculated. And then the real-time compensation of the overall axial errors of the spindle on the whole working table was realized. The accuracy of CNC machine are improved by using the proposed thermal error compensation method. Compared with the traditional single point thermal error compensation method, the standard deviation of the integrated model is reduced by about 7 μm after analysis, and the accuracy ratio is up to 50%.The maximum compensation residual is reduced by about 11 μm, the accuracy ratio of lift is up to 60%.

CNC machine worktable; flatness error model; thermal error model; combined error model.

2016-05-04

国家自然科学基金资助重大项目(51490660，51490661)；国家自然科学基金资助项目(51175142，E051102)

TG502.15;TH161

10.3969/j.issn.1004-132X.2017.11.012

苗恩铭，男，1971年生。合肥工业大学仪器科学与光电工程学院教授、博士研究生导师。主要研究方向为精密机械工程、精度理论、数控机床热误差补偿、机械热鲁棒性结构设计理论与应用技术。发表论文50余篇。E-mail: miaoem@163.com。徐建国，男，1991年生。合肥工业大学仪器科学与光电工程学院硕士研究生。吕玄玄，女，1994年生。合肥工业大学仪器科学与光电工程学院硕士研究生。魏新园，男，1994年生。合肥工业大学仪器科学与光电工程学院硕士研究生。