机械密封端面形貌的三维重建及其表征

张 浩 孙见君 马晨波 涂桥安

南京林业大学机械电子工程学院，南京，210037



机械密封端面形貌的三维重建及其表征

张 浩 孙见君 马晨波 涂桥安

南京林业大学机械电子工程学院，南京，210037

为了准确方便地描述机械密封端面的三维形貌及泄漏通道，基于密封环端面断层扫描二维图像，研究开发了机械密封端面形貌三维重建程序；提出了机械密封端面形貌的表征参数，并建立了基于体素的密封端面计盒维数和孔隙率算法。研究结果表明：基于断层图像的密封端面三维重建形貌能有效地反映密封端面的三维计盒维数和孔隙率等参数；层与层之间的面孔隙率具有一定的变化规律，在体孔隙率不变的情况下，改变各断层面孔隙率的分布，可以控制动静环密封端面间泄漏通道的形成及泄漏通道的大小；当采样层数较少时，采样层数对计算结果影响较大，在采样层数达到一定数值后，采样层数对计算精度的影响越来越小。

机械密封；表面形貌；三维重建；分形；孔隙率

0 引言

机械密封作为旋转设备中不可或缺的部件，在泵、压缩机及搅拌反应釜等工业装备上得到了广泛应用[1-3]。机械密封对工业装备的可靠性、安全性有着重要影响，因其失效导致的泄漏不仅会引起资源浪费、环境污染，甚至还会引发火灾、人身伤亡事故。为了揭示机械密封端面泄漏成因，人们提出了端面间隙锥角模型[4]、“波度”理论[5]和分形泄漏模型[6]等理论，将粗糙密封端面上的泄漏通道不同程度地简化为平均平行间隙、余弦间隙或锥度间隙。事实上，具有一定粗糙度的机械密封动静环在配对时，除微凸体点接触外，接触点周围均为孔隙[7]；密封端面的泄漏可能性取决于各个孔隙组成的孔隙群能否形成贯穿密封端面的通道[8]。如同工程表面一样，机械密封端面形貌通常采用基于LONGUET[9]和NAYAK[10]的统计数据获得的2D粗糙度和3D粗糙度[11]来描述，但这些统计分析法存在分布的不稳定性、测量的多尺度性和仪器的依赖性等明显的缺点。一些研究者探索采用轮廓线的二维分形维数[12]以及基于轮廓线二维分形维数D获得的三维形貌的分形维数DB=D+1[13]来表征密封端面的形貌，克服了上述不足。然而，机械密封规律性的旋转运动会使动静环磨损表面周向和径向分形维数产生一定的差异，导致同一端面采用周向轮廓与采用径向轮廓的二维分形维数或基于此获得的三维分形维数不同，这大大降低了该表达方法的有效性。

为了准确和方便地描述密封界面的泄漏通道状态，本文利用密封端面的断层二维图像，通过体素绘制方法构建密封端面三维形貌；引入三维分形维数和孔隙率来表征密封端面几何形状复杂性和孔隙分布信息，研究建立基于体素的密封端面计盒维数和孔隙率计算方法，从而为机械密封的泄漏研究提供一种新的思路和方法。

1 密封端面三维重建

三维重建包括面绘制和体绘制两类。面绘制分为基于轮廓的表面重建和基于等值面的间接体素三维重建；体绘制包括体光线跟踪法和体单元投影法[14]。LORENSEN等[15]在深入研究面绘制的算法后，提出了一种重建效果好、速度快、基于体素的等值面三维重建技术，并命名为“Marching Cubes”算法，即先将相邻断层间的8个网格点组成的单元定义为体素，然后确定一个表面阈值，计算每一个体素内的梯度值，并与表面阈值进行比较判断，找出包含在等值面内的顶点，查找给定的索引表，确定体素的三角剖分形式，再利用差值的方法绘制构造体素的表面。本文提出的密封端面三维重建流程如图1所示。

图1 密封端面三维重建流程图Fig.1 Flowchart of 3D reconstruction of mechanical seal end face

1.1 二维断层图像获取

(1)测量仪器。采用奥林巴斯OLS4100激光共聚焦显微镜对密封环端面进行断层扫描，在扫描过程中需要保证激光共聚焦显微镜镜头的光轴垂直于样品表面，采样的高度为扫描范围内三维形貌最大高度，即从微凸体的最低谷到最高峰，图2为扫描原理示意图。测量范围：x、y向0～127 μm，z向0～1.6 μm；测量分辨率：x、y向0.12 μm，z向0.01 μm。

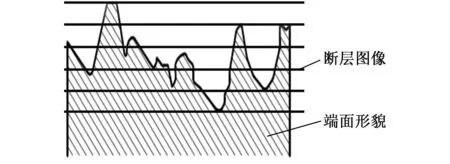
图2 表面形貌的断层扫描原理Fig.2 Scanning principle for surface topography

(2)试样。试样为浸渍酚醛树脂碳石墨环，端面尺寸为：内径53.0 mm，外径61.0 mm。

(3)测量结果。在测量范围内对密封环三维形貌进行断层扫描，采样高度1.6 μm，共采集32幅图像，每层间距0.05 μm，图像大小为1024×1024像素，放大倍数为2041。考虑到计算机的计算能力，将图像尺寸截取为512×512像素，图3为部分断层图像。

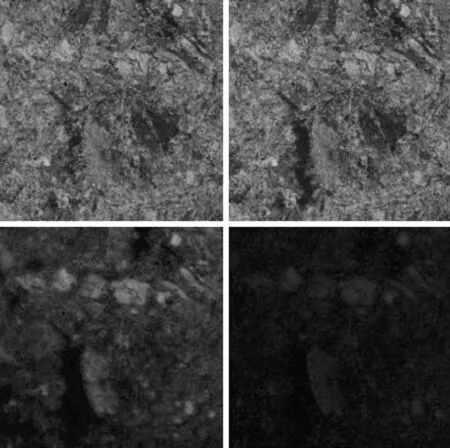
图3 部分断层图像Fig.3 Sectional images

1.2 二维断层图像预处理

图像预处理采用MATLAB完成。首先将原始RGB图像转换为灰度图像；为了克服采集过程中因扫描环境和扫描参数影响导致图像曝光过度或曝光不足产生的对比度不明显问题，对图像中每一个像素的灰度级进行标度变换，以扩大图像灰度范围，改善图像质量；然后进行直方图均衡化，将原始图像的灰度分布均匀化，在不影响整体对比度的情况下，增大目标与背景的反差，增强图像暗部信息；进而通过平滑滤波，消除图像在采集、传输和显示过程中受到干扰而产生的噪声，并保护图像的边缘信息；最后，将Otsu法计算的灰度值作为阈值对图像进行分割，分割后图像以只包含0和1的二值矩阵形式保存在计算机中，其中0代表密封端面的孔隙，1代表密封端面的固体骨架。图4为预处理前和预处理后的图像。

(a)预处理前 (b)预处理后图4 预处理前后图像的比较Fig.4 Comparison of images before and after preprocessing

1.3 基于体素的三维重建

将处理好的二维断层图像依照顺序读入MATLAB中，通过构造多维数组创建一个二值的三维体素矩阵M(体数据的长度l×宽度w×高度h为512×512×32)，计算体数据集在显示平面的累计投影，并对碎片进行构造，定义图像颜色和光线，再设置图像的显示效果。图5为浸渍酚醛树脂碳石墨环端面三维重建效果图。

图5 石墨环端面三维重建效果图Fig.5 Image of 3D reconstruction of graphite ring end face

2 密封端面的形貌表征

图5所示的密封端面三维形貌不仅给出了研究表面的直观图像,还反映了表面几何形状的复杂程度。由于计盒数法数学表达简单，物理含义直观[16]，计算粗糙程度近似于磨削表面的三维分形维数最为准确[17]，所以本文采用计盒数法求解三维重建密封端面的分形维数；考虑到区别几何形状复杂程度相近的表面，以及为后续的动静环接触端面间泄漏通道的研究提供便利，拟引入各断层面孔隙率和体孔隙率来描述密封端面的差异。

2.1 三维分形维数

2.1.1 基于体素的计盒维数计算原理

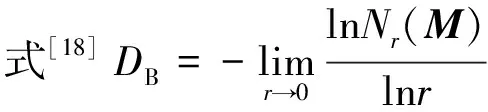
由于三维体素矩阵M是由二维断层图像叠加而成的，因此矩阵中的体素和二维图像中的像素一样具有离散性，即当用边长为r的立方体覆盖时，其最小立方体为一个体素。综合考虑计算机内存和计算精度，边长序列采用下式[19]构造：

(1)

式中，c为等分数。

利用MATLAB完成上述程序的设计，其流程如图6所示。

图6 MATLAB求取三维分形维数流程图Fig.6 Flowchart to calculate 3D fractal dimension using MATLAB

2.1.2 三维计盒维数计算

对密封端面上随机选取的4个采样区域A、B、C、D组成的三维体素矩阵进行计算，结果如表1所示，不同区域的拟合直线如图7所示。

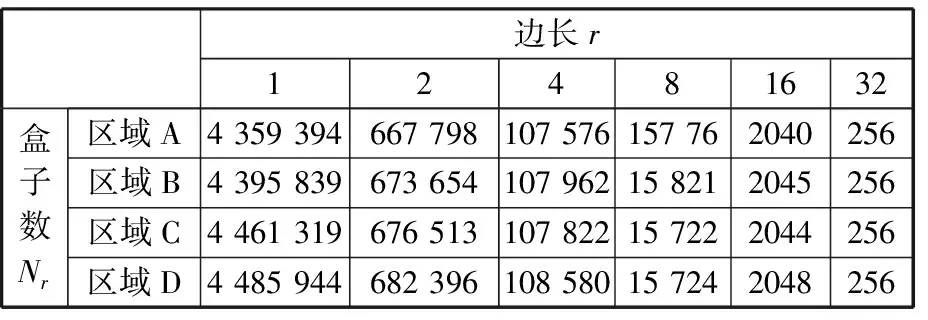
表1 不同区域盒子边长与盒子数关系

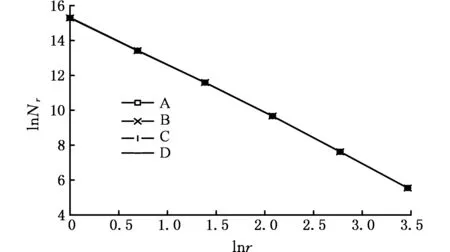
图7 不同区域的拟合直线Fig.7 Fitting lines of different areas

对于A、B、C、D四组数据，拟合方程和相关数据如表2所示。

表2 拟合方程及相关数据

从表2中可以看出，4个区域的拟合方程都具有很强的线性相关度，4组分形维数之间的极差为0.0086，且与文献[17]中关于工程表面的分形维数计算结果相近。上述数据表明，重建的密封端面具有较高的精度，能较准确地反映密封端面具有的分形特征，同时也表明一定精度范围内未磨损密封环的粗糙端面是各向同性的[20]。

2.2 孔隙率

2.2.1 孔隙率计算原理

对于图4b所示的二值图像，可以通过统计像素的方法计算目标像素(孔隙)占图像总像素的比例，则密封端面二值化断层图像面孔隙率可利用下式计算：

φS=S0/(S0+S1)

(2)

式中，S0为图像中目标像素(孔隙)个数；S1为图像中背景像素(固体骨架)的个数，且S=S0+S1；S为图像总像素数。

推广到三维空间，对于图5所示的重建形貌，同样可利用统计体素的方法求取目标体素(孔隙)占总体素数的比例，则三维密封端面体孔隙率可利用下式计算：

φV=V0/(V0+V1)

(3)

式中，V0为三维密封端面中目标体素(孔隙)的个数；V1为三维密封端面中背景体素(固体骨架)的个数，且V=V0+V1；V为三维体素矩阵总体素数。

2.2.2 孔隙率计算

利用MATLAB开发的程序求取32幅二维断层扫描图像每一层图像的面孔隙率，层数与面孔隙率的对应关系如图8所示。可以看出，随着层数的增加，面孔隙率逐渐增大，且在20层至30层内上升幅度明显增大，这说明密封端面形貌在这一层数区间内变化较大。统计图5所示的三维体素矩阵中目标体素(孔隙)的个数V0和总的体素个数V，可以得到体孔隙率φV=V0/V=38.59%。需要说明的是，体孔隙率与测量仪器的分辨率有关，不同分辨率仪器测量的密封环，其体孔隙率可能会存在较大的差异。

图8 层数与面隙率关系Fig.8 Relations between layers and surface porosities

2.3 采样层数对计算结果的影响

为了进一步探究采样层数与分形维数和孔隙率的关系，以相同的处理计算方法对区域D在不同采样层数下的分形维数和孔隙率进行计算，结果如图9所示。可以看出，当采样层数较小时，无论是分形维数还是孔隙率的相对变化幅度都比较大；当层数超过16层之后，二者的变化幅度趋于平缓，即当采样层数大于16之后，增大层数并不能大幅提高计算结果的精度。此外，较大的采样层数会成倍地增加计算机处理时间，降低计算效率。因此，在综合考虑计算精度和计算效率的前提下，本文采样层数选取32是合理可行的。

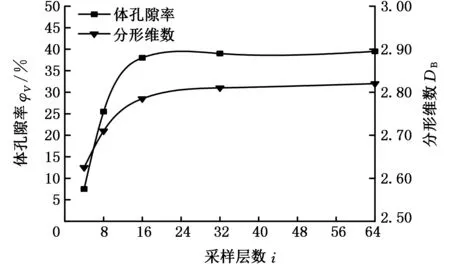
图9 采样层数对体孔隙率和分形维数的影响Fig.9 Influences of layer numbers on volume porosities and fractal dimensions

3 结论

(1)研究开发了基于二维断层扫描图像的密封端面形貌三维重建程序，通过MATLAB实现了密封端面形貌的三维重建；提出了基于体素的计盒维数和孔隙率表征方法，验证了密封环端面的各向同性特征。

(2)孔隙率随着层数的递增而变大，即密封端面底部形貌主要由固体骨架组成，顶部形貌主要由孔隙组成，同时靠近顶部区域的形貌变化幅度比底部区域的剧烈；在体孔隙率不变的情况下，通过改变各断层面孔隙率的分布，可以控制动静环密封端面间泄漏通道的形成及泄漏通道的大小。

(3)当采样层数小于16时，计算结果稳定性差，精度低；当采样层数大于16时，计算的分形维数逐步稳定在2.82左右，而体孔隙率逐步稳定在38.5%左右，此时再过多地增加层数并不能大幅度提高计算精度。

(4)密封环端面的泄漏通道反映在本文的三维数据中即为相互连通的体素，因此本文提出的基于体素的描述方法能够为后续的动静环接触端面间泄漏通道的研究提供便利。

[1] BRACCESI C, VALIGI M C. Undesired Acoustic Emissions of Mechanical Face Seals: Model and Simulations[J]. Tribology International, 2014, 71: 125-131.

[2] GOILKAR S S, Hirani H. Parametric Study on Balance Ratio of Mechanical Face Seal in Steam Environment[J]. Tribology International, 2010, 43(5/6): 1180-1185.

[3] 孙见君, 魏龙, 顾伯勤. 机械密封的发展历程与研究动向[J]. 润滑与密封, 2004(4): 128-131,134. SUN Jianjun, WEI Long, GU Boqin. Development Course and Research Trend on the Mechanical Seal[J]. Lubrication Engineering, 2004(4): 128-131,134.

[4] GREEN I. A Transient Dynamic Analysis of Mechanical Seals including Asperity Contact and Face Deformation [J].Tribology Transaction, 2002, 45(3): 284-293.

[5] LEBECK A O. Hydrodynamic Lubrication in Wavy Contacting Face Seal: a Two-dimensional Model[J]. Journal of Lubrication Technology, 1981, 103(4): 578-586.

[6] 孙见君, 顾伯勤, 魏龙. 基于分形理论的接触式机械密封泄漏模型[J]. 化工学报, 2006, 57(7): 1626-1631. SUN Jianjun, GU Boqin, WEI Long. Leakage Model of Contacting Mechanical Seal Based on Fractal Geometry Theory[J]. CIESC Journal, 2006, 57(7): 1626-1631.

[7] PERSSON B N J. Fluid Dynamics at the Interface Between Contacting Elastic Solids with Randomly Rough Surfaces[J]. Journal of Physics: Condensed Matter., 2010, 22 : 1-15.

[8] BOTTIGLIONE F, CARBONE G, MANTRIOTA G. Fluid Leakage in Seals: an Approach Based on Percolation Theory[J]. Tribology International, 2009, 42(5): 731-737.

[9] LONGUET H. The Statistical Analysis of a Random Moving Surface[J]. Philosophical Transactions of the Royal Society of London, Series A, 1957, 249: 321-387.

[10] NAYAK P. Some Aspects of Surface Roughness Measurement[J]. Wear, 1973, 26: 165-174.

[11] WIZNER M, JAKUBIEC W, STARCZAK M. Description of Surface Topography of Seal Rings[J]. Wear, 2011, 271: 571-575.

[12] ZHU H, GE S R, HUANG X L, et al. Experimental Study on the Characterization of Worn Surface Topography with Characteristic Roughness Parameter[J]. Wear, 2003, 255: 309-314.

[13] 葛世荣. 粗糙表面的分形特征与分形表达研究[J]. 摩擦学学报, 1997, 17(1): 73-81. GE Shirong. The Fractal Behavior and Fractal Characterization of Rough Surfaces[J]. Tribology, 1997, 17(1): 73-81.

[14] SENTHIL K T, ANUPA V. 3D Reconstruction of Face From 2D CT Scan Images[J]. Procedia Engineering, 2012, 30: 970-977.

[15] LORENSEN W, CLINE H. Marching Cubes: a High Resolution 3D Surface Construction Algorithm[J]. Computer Graphics, 1987, 21(4):163-169.

[16] FALCONER K J. Fractal Geometry-mathematical Foundations and Applications[J]. Biometrics, 1990, 46(4):499.

[17] 李成贵, 董申. 三维表面形貌的分形维数计算方法[J]. 航空精密制造技术, 2000, 36(4): 36-40. LI Chenggui, DONG Shen. Counting Methods of Fractal Dimension for 3D Surface Topography[J]. Aviation Precision Manufacturing Technology, 2000, 36(4): 36-40.

[18] 朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011: 9-38. ZHU Hua, JI Cuicui. Fractal Theory and Its Applications[M]. Beijing: Science Press, 2011: 9-38.

[19] 毛灵涛, 连秀云, 郝丽娜. 基于数字体图像三维裂隙的分形计算及应用[J]. 中国矿业大学学报, 2014, 43(6):1134-1139. MAO Lingtao, LIAN Xiuyun, HAO Lina. The Fractal Calculation of 3D Cracks Based on Digital Volumetric Images and Its Application[J]. Journal of China University of Mining & Technology, 2014, 43(6):1134-1139.

[20] 孙见君, 何小元, 徐建中, 等. 机械密封端面形貌分形行为[J]. 石油化工设备, 2007, 36(6): 15-18. SUN Jianjun, HE Xiaoyuan, XU Jianzhong, et al. Study on Fractal Behaviors of Surface Topography of Mechanical Seals[J]. Petro-chemical Equipment, 2007, 36(6): 15-18.

(编辑 苏卫国)

3D Reconstruction and Characterization for Surface Topography of Mechanical Seals

ZHANG Hao SUN Jianjun MA Chenbo TU Qiaoan

School of Mechanical and Electrical Engineering，Nanjing Forestry University，Nanjing，210037

In order to characterize the surface 3D topography and leakage path of mechanical seal end faces accurately and conveniently, a 3D reconstruction program for surface topography of mechanical seal end faces was developed and studied based on 2D sectional images. A new characterization parameter for surface topography of mechanical seal end faces was proposed and based on voxel an algorithm was established to calculate the fractal dimensions and the porosity. The results show that it is effective to reflect the 3D box-counting dimension, porosity and other parameters of surface topography of mechanical seal end faces with 3D reconstruction based on sectional images. The surface porosity of different layers has a law of change, so when the volume porosity is constant, the formation and the scale of leakage path of mechanical seal end faces will be dominated by the change of surface porosity distribution on different sectional images. The sampling number of layers have a great influence on the calculating results when it is fewer, however, the influence becomes smaller as the number reaches a certain value.

mechanical seal； surface topography； 3D reconstruction； fractal； porosity

2016-05-11

国家自然科学基金资助项目(51375245,51505230)；江苏省自然科学基金资助项目(BK20130976)

TH136

10.3969/j.issn.1004-132X.2017.11.006

张 浩，男，1990年生。南京林业大学机械电子工程学院硕士研究生。主要研究方向为工程摩擦学及密封技术。E-mail:15295575718@163.com。孙见君，男，1965年生。南京林业大学机械电子工程学院教授、博士研究生导师。马晨波，男，1983年生。南京林业大学机械电子工程学院副教授、硕士研究生导师。涂桥安，男，1957年生。南京林业大学机械电子工程学院教授。