双螺杆压缩机转子啮合线与型线关系研究

何雪明 姜振钢 武美萍 张 荣 纪小刚

1.江南大学江苏省食品先进制造装备技术重点实验室,无锡,2141222.江南大学理学院,无锡, 214122

双螺杆压缩机转子啮合线与型线关系研究

何雪明1姜振钢1武美萍1张 荣2纪小刚1

1.江南大学江苏省食品先进制造装备技术重点实验室,无锡,2141222.江南大学理学院,无锡, 214122

从双螺杆压缩机转子啮合线出发，详细介绍了啮合线法，利用啮合关系与型线坐标转换关系推导出阴阳转子型线的方法。给出了啮合线法中的连续性要求并提供了相应的求解步骤，解决了啮合线法设计转子型线过程中的连续性问题。研究了啮合线的3个关键控制点，并总结了其位置变化对转子型线(阴阳转子的齿心角、齿厚以及齿间面积)的影响。最后利用啮合线法设计了一条新型线，并演示了通过改变关键控制点位置的方法提高了新型线排量的方法，提高了设计效率。

双螺杆压缩机；转子型线；啮合线法； 关键控制点

0 引言

双螺杆压缩机的阴阳转子作为整个压缩机中最重要的零件，它的性能对双螺杆压缩机的性能有着决定性的影响，因此许多国内外学者将其作为研究重点，开展了众多研究，主要研究内容为阴阳转子型线设计方法和新型线的开发。

现有的绝大部分转子型线都是由转子法[1-3]推演得到的，该方法先选择阴阳转子中的其中一个为设计对象，然后在其坐标系内设计出二维曲线作为其齿形曲线，接着根据包络条件推导出啮合条件式，建立出转角与曲线参数之间的一一对应关系，结合坐标转换即可得到对应的需要设计的另一齿的齿形。由这种方法设计的型线主要有SRM系列型线、复盛型线、日立型线、寿力型线等。

MENSSEN等[4]在20世纪70年代提出了采用齿条法设计加工早期的阴阳转子型线的方法， RINDER[5]在1984年提出了齿条法设计方法，并在3年后设计出了相应的转子型线。STOSIC等[6-9]在齿条法上进行改进提出了新的N型线设计方法。周志宏等[10]及陈碧楠等[11]分别采用转子法和齿条法对转子型线进行了推演设计，得到了较优的型线参数。齿条法与转子法相似，只是在设计型线时是在齿条上设计阴阳转子型线，再根据啮合关系推演设计齿形的共轭曲线，得到另一齿的齿形。这两种方法可以统称为转子型线正向设计方法，在设计时二者之间可以交互使用。

不论是转子法还是齿条法，都是在阴阳转子型线设计后，通过复杂的计算才能求得啮合线方程。在得到转子啮合线后对双螺杆压缩机的性能作出初步评估然后返回对转子型线进行多次修改以改善转子性能，最后在对各个参数优化之后确定最后型线。这一设计过程耗时费力，设计效率低下，为了改变这一现状, ZAYTSEV等[12-13]和WU等[14-16]提出基于反向思维方式，利用可以预测转子型线性能的啮合线来设计转子型线。徐健等[17-20]采用齿廓法线法，演示了啮合线法的设计方法。何雪明等[21]研究了齿廓法线法，并从理论上推导了啮合线段为直线、圆弧、三次B样条曲线的阳转子型线方程。本文也采用这种思想，从啮合线出发，对啮合线进行设计，将啮合原理中的齿廓法线法作为包络条件反推转子型线。

1 啮合线法型线设计原理

在双螺杆压缩机中，两个转子相互啮合转动，一般是由阳转子带动阴转子转动。两个转子齿面相互接触形成的空间曲线称为接触线(图1)，将接触线投影到垂直于轴线的平面上，它也是阴阳转子型线啮合时啮合点的轨迹，称为啮合线。

图1 转子上的接触线Fig.1 Contact line of the rotor surface

转子啮合时，在空间接触线的任意一点处的速度方向即为该点处的切线方向，该方向与该点的法线方向是互相垂直的，假设该点处的切线方向向量为v，法线方向向量为n，则两者之间的关系式为

n·v=0

(1)

根据此关系可以由啮合线方程推导出阴阳转子啮合线的方程。首先建立相应的转子坐标系，主要包括啮合线坐标系和阴阳转子动坐标系。图2所示为阴阳转子动静坐标系和啮合线坐标系之间的关系，下标0表示啮合线，下标1表示阳转子，下标2表示阴转子。图2中，O0x0y0是原点在阴阳转子切点固接于机壳上的啮合线坐标系，O2x2y2、O1x1y1是阴阳转子对应的动坐标系，这三个坐标的z轴均是沿着轴线向外的方向。根据阴阳转子传动中的一些已知条件，可得

(2)

R1+R2=A

(3)

φ1+φ2=(1+i)φ1=kφ1

(4)

式中，i为阳阴转子齿数比；φ1为阳转子动坐标系逆时针旋转的角度；φ2为阴转子动坐标系顺时针旋转的角度；ω2、ω1分别为阴阳转子的角速度；n2、n1分别为阴阳转子的转速；R2、R1分别为阴阳转子的节圆半径；z2、z1表示阴阳转子的齿数。

图2 转子型线坐标系关系Fig.2 Relationship of rotor profile coordinate

在利用啮合线法反向设计时，啮合线的各段曲线是预定义的，其方程是已知的，假设其中某段的啮合曲线参数方程为

(5)

ts≤t≤te

通过坐标变换可推导啮合线坐标系O0x0y0和阳转子动坐标系O1x1y1之间的转换关系:

(6)

阴阳转子动坐标系O2x2y2和O1x1y1之间的转换关系为

(7)

为了得到包络条件即φ1关于t的函数，需先将阴阳转子型线上的对应点转换到同一坐标系中，然后再利用式(1)，计算得到包络条件式。本文利用式(7)先将阴转子型线上的点转换到动坐标系O1x1y1下，再由式(6)计算得到包络条件式,因此n和v分别为

(8)

将式(8)代入式(1)可得

(9)

式(7)的两式分别对t和φ1求偏导，并代入式(9)可得关于t和φ1的偏导数方程(只含有x1、y1)，整理化简可得

(10)

式(6)的两式求偏导数，并代入式(10)可得啮合线参数t与阳转子型线位置参数φ1之间的关系，整理化简得

(11)

根据转子半径R与齿数比i之间的关系，可知Ai=kR1，故可将式(11)进一步简化：

(12)

式(12)中除了φ1与t是未知的，其余均已知，因此可将式(12)表达为关于参数t的φ1函数，为了方便观察可将式(12)表达为

(13)

对式(13)进行积分，可得

(14)

式(14)中，φ0为常数。啮合线方程的参数t决定了阳转子型线齿形，并与之是一一对应关系，只需知道啮合线方程x0、y0和阳转子半径R1，即可得到阳转子型线方程。

本文推导的啮合线法，修正了文献[21]中方程的小错误。本文通过将阴转子的型线坐标转换到阳转子坐标系中，再由阳转子坐标系转换到啮合线坐标系，最终在啮合线坐标系下表达阳转子型线的位置参数φ1与啮合线参数t之间的关系，即得到了阳转子的型线方程;同样也可以从阳转子出发，将阳转子的型线方程在阴转子坐标系下表达，最后转换到啮合线坐标系下，得到阴转子型线位置参数φ2与啮合线参数t之间的关系。

2 啮合线法转子型线连续性

根据前文可以求得啮合线中每段曲线对应的转子型线方程，但由于式(14)中常数项的存在，每一段所对应的转子型线的位置是不定的，而实际当中转子型线是连续光滑的；因此在利用啮合线法设计转子型线时也必须考虑到这一点，保证转子型线的前后连续光滑。

φ1=f(t)+φ0

(15)

如图3所示，假设AB1段是由上一段啮合线线型中的一种所得转子型线，在设计B2C段时，需要求解φ0确定B2C的位置，以保证前后两端曲线连续，φ0可按照图4所示流程计算得到，如此便可使得B1、B2两点重合，保证AB、BC之间的连续性。首先提取B1点坐标，假设阳转子型线上B1点的坐标为(xe,ye)，将该点代入式(6)中可求解sinφ1e、cosφ1e的值:

(16)

φ0=φ1e-f(t0)

(17)

图3 转子型线连续性要求示意图Fig.3 Continuity requirement of rotor profile

图4 φ0求解流程图Fig.4 Flow chart of the process to solve φ0

性能优良的转子型线应当具有较好的加工性能、高效的压缩效率和低的齿面磨损，即要求转子齿面尽量光滑，没有尖点，具有较短的空间接触线、较小面积的泄露气孔、低的齿面滑动和扭转偏移。在转子型线的连接时，除了需要保证其一阶连续，还需使其达到二阶连续。要实现这一要求，则需要保证定义的啮合线所生成的转子型线是一条光滑的曲线。以O1为圆心的圆弧啮合线会在型线上产生一个尖点，这种情况应尽量避免，阴转子也一样,因此，不应将以转子轴心为圆心的圆弧段作为啮合线的设计组成，在啮合线之间的线型连接中需要保证其相切。

3 啮合线与转子型线关系

文献[21]中指出了啮合线的本身形式和参数会影响到型线的形状特征。本文继续对啮合线进行研究，并整理出了3个关键控制点，研究其位置变化对型线产生的影响。本文主要研究单边型线，即其啮合线只存在于啮合线坐标系的第二与第三象限。如图5所示，啮合线由4个控制点划分为4个部分，a为啮合线坐标原点，b为啮合线最低点，c为啮合线与x轴交点，d为啮合线最高点。第Ⅰ部分在啮合线坐标系的第三象限内，为从原点O0(a)开始沿着顺时针到达最低点b所形成的曲线，第Ⅱ部分在第三象限内，为从b点到达啮合线与x0轴形成的交点c之间的曲线，第Ⅲ部分则是第二象限内c点到最高点d之间的曲线，第Ⅳ部分则是从最高点d回到原点O0(a)的曲线。

图5 啮合线段和转子型线上的相应曲线段Fig.5 Meshing line segments and the response curve segments on the rotor profile

啮合线被4个控制点a、b、c、d分成4个部分，除了a点之外，其余3个关键控制点对转子型线的影响也是最为明显的，本文通过其多个位置变化对转子型线的影响进行研究。

以b点为例，对啮合线与转子型线进行研究，b点可以沿着x轴方向和沿着y轴方向平移到不同位置点，在改变b点位置时保持其他控制点位置和线型不变。对比不同位置下的b点所生成的啮合线所对应的转子型线。b点沿x轴方向不同位置的三种啮合线和型线如图6所示。b点沿y轴不同位置的三种啮合线和型线如图7所示。

图6 b点沿x轴方向不同位置的啮合线和阴阳转子型线分布关系Fig.6 Distribution of male & female rotor profiles where b point at the different positions along the x-axis direction of the meshing line

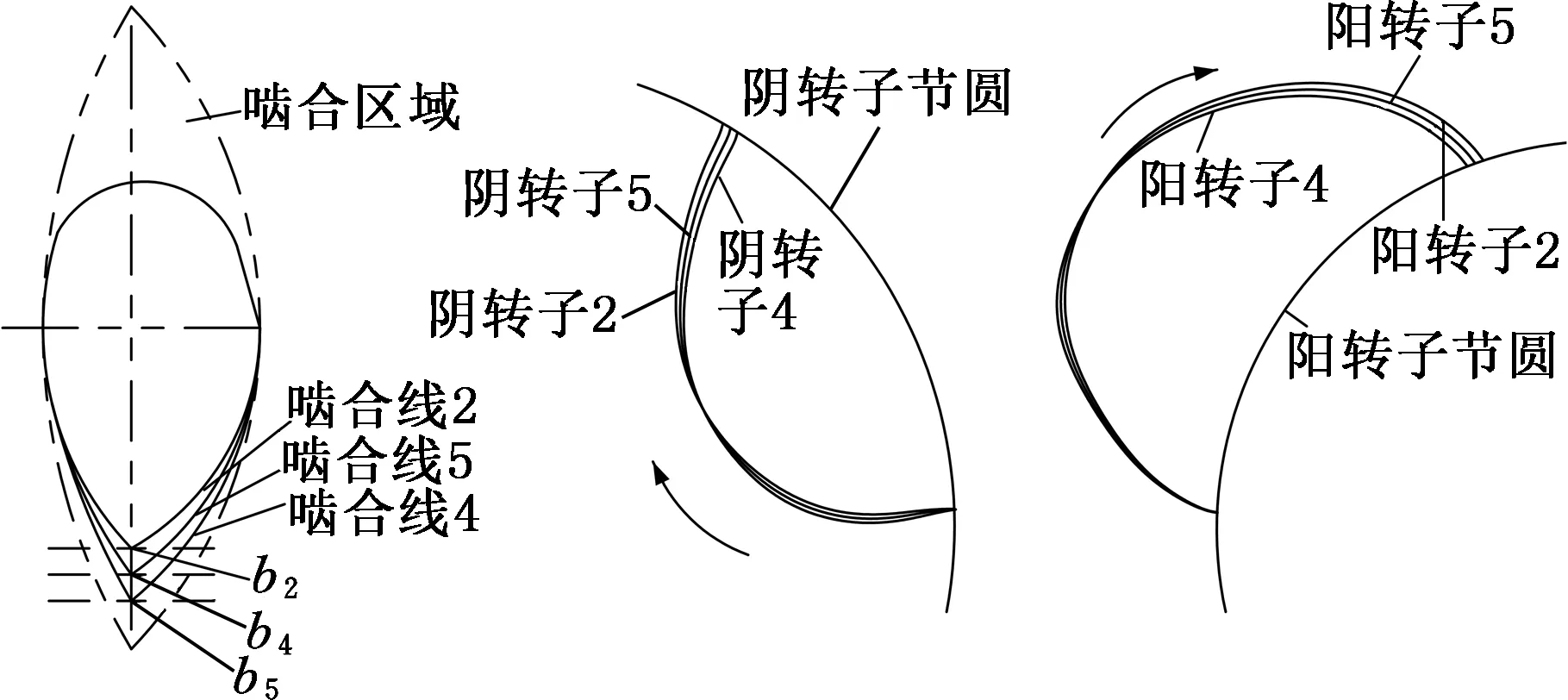
图7 b点沿y轴方向不同位置的啮合线和阴阳转子型线分布关系Fig.7 Distribution of male & female rotor profiles where b point at the different positions along the y-axis direction of the meshing line

a点必须与啮合线坐标系原点重合，在此不展开研究。利用与b点相同的方法对c点和d点分别展开研究，可得表1所示规律。

总体而言，啮合线的关键控制点对转子型线的影响如下：

(1)在b点，以b点为原点建立坐标系，则b点在第一象限内和靠近第一象限的二四象限内，

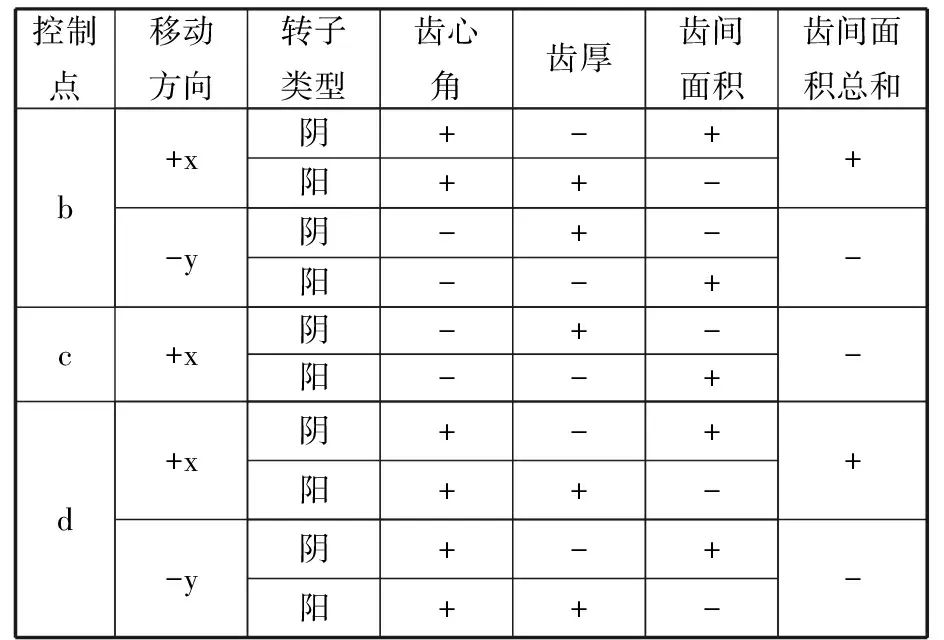
表1 啮合线关键控制点对转子型线的影响Tab.1 Influence of key control points of meshing line on rotor profile

阴阳转子齿心角较大，阴转子齿厚较小，阳转子齿厚较大，齿间面积总和变大，b点在第三象限内和靠近第三象限的二四象限内，则正好相反。

(2)在c点，随着c点沿水平方向从左向右移动(即ac距离减小)，阴阳转子啮合区域变小，齿心角减小，阴转子齿根圆直径增大，阳转子齿顶圆直径减小，阴转子齿厚增大，阳转子齿厚减小，齿间面积总和逐渐减小。

(3)在d点，以d点为原点建立坐标系，则d点在第四象限内和靠近第四象限的一、三象限内，阴阳转子齿心角较大，阴转子齿厚较小，阳转子齿厚较大，齿间面积总和变大，d点在第二象限内和靠近第二象限的一三象限内，则正好相反。

4 啮合线法转子型线设计

根据表1的汇总结果，在设计转子型线时可根据如下规则快速实现对型线的优化：若要增大齿间面积总和，则可以通过增大b点的x或y坐标值，或减小c点的x坐标值，或增大d点的x坐标或减小y坐标值来实现。通过整理表1中的数据，将设计目标为增大阴阳转子的齿心角、齿厚以及齿间面积总和的调整方法列于表2。

表2 设计目标与控制点移动方向

表2中“阴”表示阴转子；“阳”表示阳转子；+x表示向x轴正方向移动，即增大x坐标值；-y表示向y轴负方向移动，即增大y坐标值；若设计目标为减小上述参数，则b、c、d点的移动方向全部取反。

参照表3中的数据，目前大部分的双螺杆压缩机生产厂家生产的都是以6∶5为比例的转子。本文以主流的6∶5齿为研究对象，中心距260 mm作为基本设计参数，利用啮合线法设计新型线。

表3 螺杆压缩机现状

如图8所示，在啮合线坐标系O0x0y0中从原点出发顺时针设计一条啮合线1，该啮合线主要分成7段，前面5段主要是以圆弧为线型，第6段则以直线作为啮合线线段，实现啮合线封闭，在原点处G10与A10重合，是由两圆弧在节圆切点处相互啮合形成的点，点G10作为啮合线的一段，在阴阳转子型线上有对应的型线。在啮合线1中4个控制点在啮合线坐标系中的坐标(单位为mm)为a(0, 0)、b(-38, -77)、c(-63.7, 0)、d(-33.8, 33)。具体每一段的曲线类型如表4所示。啮合线1对应的完整阴阳转子如图9所示。

上述型线的阴阳转子齿间面积总和为107 978.10 mm2，我们希望得到更大的齿间面积，以增加该齿形的排量，接下来则在啮合线1的基础上以增大齿间面积总和为设计目标，利用表2中增大齿间面积方法进行调整，减小c点的坐标值，得到啮合线2。

图8 啮合线1和对应的阴阳转子型线齿廓Fig.8 The corresponding male & female rotor profiles of meshing line 1

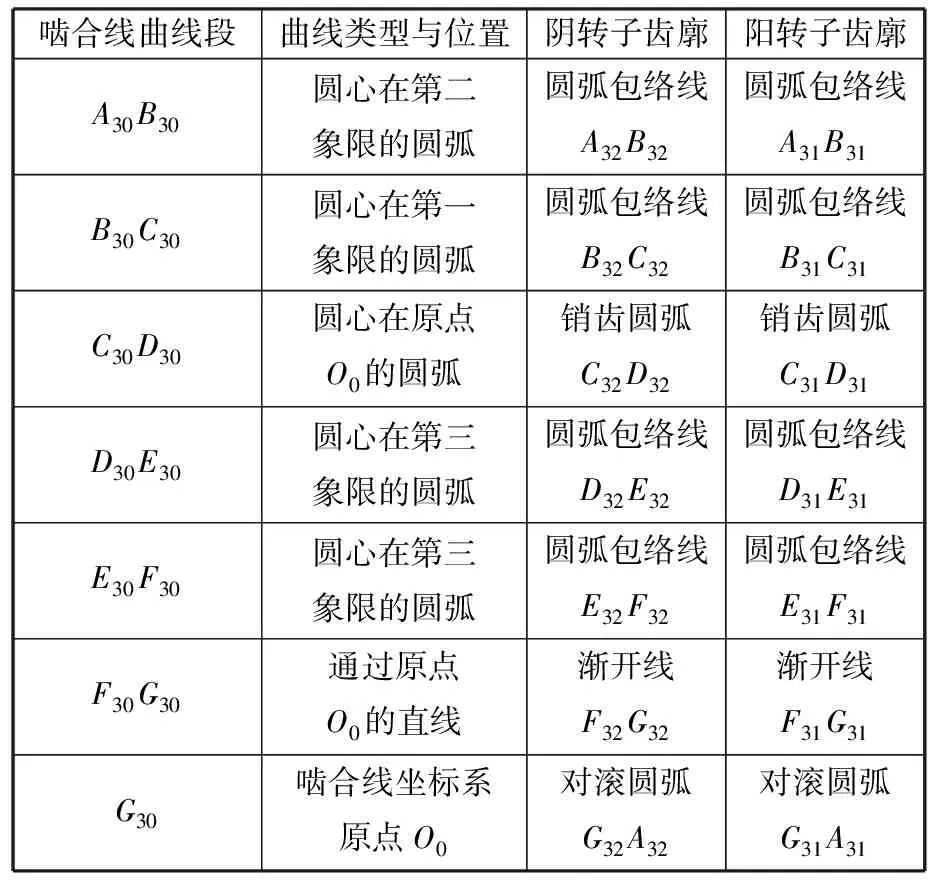
表4 设计实例中的各段啮合线与齿廓曲线描述

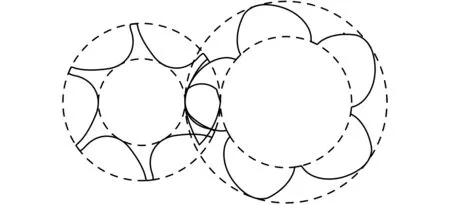
图9 啮合线1与完整阴阳转子型线Fig.9 The complete corresponding male & female rotor profiles of meshing line 1

如图10所示，啮合线2 主要是增大了控制点a、c之间的距离，而各个曲线段的线型和其余控制点位置保持不变，4个控制点在啮合线坐标系中的坐标(单位为mm)为a(0, 0)、b(-38, -77)、c(-66.7, 0)、d(-33.8, 33)。啮合线2对应的完整阴阳转子如图11所示。

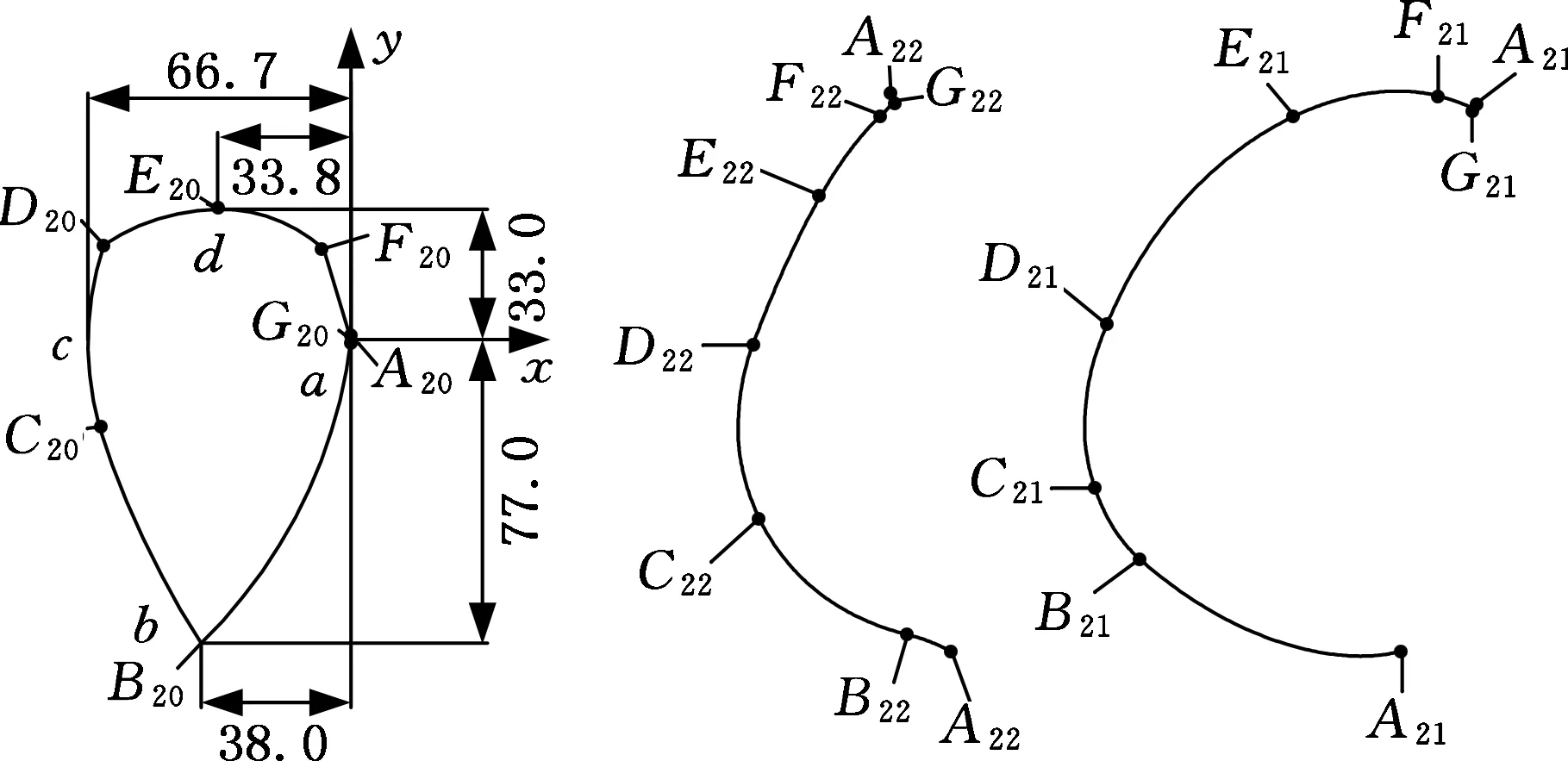
图10 啮合线2和对应的阴阳转子型线齿廓Fig.10 The corresponding male & female rotor profiles of meshing line 2

图11 啮合线2与完整阴阳转子型线Fig.11 The complete corresponding male & female rotor profiles of meshing line 2

从图10中可以看出阴阳转子型线2和阴阳转子型线1有很大的差别，将这两个转子型线在同一坐标系下进行对比，如图12所示。图12中实线表示啮合线1和其对应的阴阳转子型线，虚线表示修改后的啮合线2和阴阳转子型线。从图12中可以看出修改后的啮合线2所在的啮合区域变大，阴转子齿根圆变小齿厚变薄，阳转子齿顶圆变大齿厚增大，阴转子的齿间面积增大，齿间面积总和增大为109 116.98 mm2，和预期是一致的。修改后的啮合线2生成的阴转子型线2的齿厚太薄，在工作中很容易折断，加工制造时也有一定的难度，所以需要进一步优化。

图12 啮合线1与啮合线2对比图Fig.12 Comparation of meshing line 1 with meshing line 2

啮合线2是啮合线1通过增大a、c之间的距离得到的，使得齿间面积增大，为了保持大的齿间面积，c点的位置保持不变，以增大阴转子的齿厚为设计目标，对b点和d点进行微调，根据表2结论，将啮合线2中的b点向左下角移动，d点向左上角移动，具体如图13所示，啮合线的其他位置和曲线段类型则保持不变，得到新的啮合线3，4个控制点在啮合线坐标系中的坐标(单位为mm)为a(0, 0)、b(-40, -79)、c(-66.7, 0)、d(-36.7, 38)。优化后啮合线3的齿间面积总和达到了108 274.59 mm2，虽然比啮合线2的齿间面积总和小，但与最初设计的啮合线1相比还是得到了增加。该转子型线是在保持了较大的齿间面积的同时将对应的阴转子2的齿厚增加，提高了阴转子的强度。设计过程中型线齿间面积的变化列于表5。啮合线3与完整阴阳转子型线如图14所示。

图13 啮合线3和对应的阴阳转子型线齿廓Fig.13 The corresponding male & female rotor profiles of meshing line 3

表5 设计型线的齿间面积

图14 啮合线3与完整阴阳转子型线Fig.14 The complete corresponding male & female rotor profiles of meshing line 3

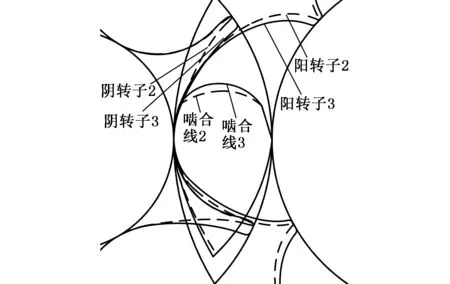
图15 啮合线2与啮合线3对比图Fig.15 Comparation of meshing line 2 with meshing line 3

图15是啮合线2与啮合线3对比图，其中虚线表示的是啮合线2及其对应的转子型线，实线表示的是啮合线3及其对应的转子型线，由于c点的位置不变，转子2和转子3的啮合区域不变，二者的阴转子齿根圆和阳转子的齿顶圆直径相等。啮合线3所对应的阴转子在后齿部分曲率变大，齿厚增大使得阴转子的几何特性得到强化，并且阴转子的几何特性也比较良好，阳转子齿厚减小，与最初相比，齿间面积总和也得到了增加，达到了最初的设计目的。

转子型线的设计是一个曲折的过程，需要进行不断的调整。啮合线法设计方法作为一种新的设计方法，可以预判型线性能，其中的关键控制点可以预判型线的大概走势，在进行型线设计时可以加快型线的设计速度，简化设计过程。在设计的过程中可以结合传统的正向设计方法， 二者之间相互结合共同完成型线设计，提高设计效率，缩短设计周期。

5 结论

(1)从双螺杆压缩机转子啮合线出发，利用齿廓法线法和坐标转换推导转子型线，详细阐述了从啮合线推导出阳转子型线的位置参数φ1与啮合线参数t之间的关系的过程。给出啮合线法中的连续性要求以及相应常数项的求解步骤，解决转子型线设计过程中连续性问题。

(2)分析讨论了啮合线的3个关键控制点对转子型线的影响。

(3)利用啮合线法设计一条新型线，并演示了利用移动啮合线的3个控制点快速地优化设计的型线，使得转子的齿间面积总和从107 978.10 mm2增加到108 274.59 mm2，而且阴阳转子的几何特性也比较良好，提高了设计效率。

[1] 邓定国,束鹏程. 回转压缩机[M]. 北京:机械工业出版社,1989：38-62. DENG Dingguo, SHU Pengcheng. Rotary Compressor[M]. Beijing: Machinery Industry Press,1989：38-62.

[2] 邢子文. 螺杆压缩机-理论、设计及应用[M]. 北京:机械工业出版社,2000:12-24. XING Ziwen. Screw Compressor-theory, Design and Application[M]. Beijing: Machinery Industry Press,2000:12-24.

[3] LITVIN F L, FENG Pinhao. Computerized Design, Generation, and Simulation of Meshing of Rotors of Screw Compressor [J]. Mechanism and Machine Theory,1997,32,(2):137-160.

[4] MENSSEN E. Screw Compressor with Involute Profile Teeth: US , 4028026[P].1977-06-07.

[5] RINDER L．Screw Rotor Profile and Method for Generating：US，4643654[P].1987-02-17.

[6] STOSIC N．Plural Screw Positive Displacement Machines：UK，9610289[P].2001-10-02.

[7] STOSIC N, HANJALIC K. Development and Optimization of Screw Machines with a Simulation Model-Part I: Profile Generation [J]. Journal of Fluids Engineering,1997,119:659-663.

[8] STOSIC N N. Profile Rotors [EB/OL].[2006-04-15]. http://www.staff.city.ac.uk/～sj376/nrot.html.

[9] STOSIC N，SMITH I K，KOVACEVIC A．Screw Compressors：Mathematical Modeling and Performance Calculation[M]．Berlin: Springer-Verlag，2005.

[10] 周志宏,李勇. 双螺杆压缩机转子圆弧及圆弧包络线型线的几何构造[J]. 机电产品开发与创新,2008,21(6):129-130. ZHOU Zhihong, LI Yong. Geometry of Arcs and Their Evolution Profile of Twin Screw Compressors[J]. Electromechanical Product Development & Innovation,2008,21(6):129-130.

[11] 陈碧楠,杨涛. 双螺杆压缩机转子型线构形及计算机辅助设计[J]. 重庆工学院学报(自然科学版),2008,22(9):36-39. CHEN Binan, YANG Tao. Design of Twin-screw Compressor Rotor Profile and Its Computer Aided Design[J]. Chongqing Institute of Technology (Natural Science),2008,22(9):36-39.

[12] ZAYTSEV D, INFANTE FERREIRA C A. Screw Compressor Rotors Profile Generation Method Based on Pre-defined Meshing Line [C]// 3rd International Compressor Technique Conference. Wuxi,2001:117-127.

[13] ZAYTSEV D, INFANTE FERREIRA C A. Profile Generation Method for Twin Screw Compressor Rotors Based on the Meshing Line [J]. International Journal of Refrigeration,2005,28(5):744-755.

[14] WU Yuren, FONG Zhanghua. Improved Rotor Profiling Based on the Arbitrary Sealing Line for Twinscrew Compressors [J]. Mechanism and Machine Theory,2008,43(6):695-711.

[15] WU Yuren, FONG Zhanghua. Rotor Profile Design for the Twin-screw Compressor Based on the Normal-rack Generation Method [J]. Journal of Mechanical Design,2008,130(4):0426011-0426018.

[16] WU Yuren, CHI Jenwei. A Numerical Method for the Evaluation of the Meshing Clearance for Twin Screw Rotors with Discrete Tooth Profile Points [J]. Mechanism and Machine Theory,2013,70:62-73.

[17] 徐健,余宾宴,余小玲,等. 螺杆压缩机转子型线设计方法[J]. 压缩机技术,2012(2):1-6. XU Jian, YU Binyan, YU Xiaoling, et al. Study on Rotor Profile Design of Screw Compressors[J]. Compressor Technology,2012(2):1-6.

[18] 徐健,许岭松,余小玲,等. 螺杆转子齿形中圆弧-圆弧包络线啮合副的研究 [J]. 压缩机技术,2012(3):1-6. XU Jian, XU Lingsong, YU Xiaoling, et al. Study on Meshing Pair of Circular-circular Envelope Curve in the Profile Design of Screw Rotors [J]. Compressor Technology,2012(3):1-6.

[19] 徐健,许岭松,余小玲,等. 一种基于齿条法的螺杆转子型线设计方法 [J]. 压缩机技术,2012(4):1-6. XU Jian, XU Lingsong, YU Xiaoling, et al. Study on Rotor Profile Design of Screw Compressors Based Upon Rack Generation Method [J]. Compressor Technology,2012(4):1-6.

[20] 徐健,周恩民,许岭松,等. 基于啮合线法的螺杆转子型线设计方法 [J]. 压缩机技术.2013(1):1-7. XU Jian, ZHOU Enmin, XU Lingsong, et al. Study on Rotor Profile Design of Screw Compressors Based Upon Meshing Line Method [J]. Compressor Technology,2013(1):1-7.

[21] 何雪明,童洁,戴进,等. 双螺杆转子型线的反向优化设计及应用[J]. 机械设计与研究,2015,31(4):151-157. HE Xueming, TONG Jie, DAI Jin, et al. Reverse Optimization Design and Application of Screw Rotor Profiles [J]. Machine Design and Research,2015,31(4):151-157.

(编辑 袁兴玲)

Research on Relationship between Rotor Profiles and Meshing Lines in Twin-screw Compressors

HE Xueming1JIANG Zhengang1WU Meiping1ZHANG Rong2JI Xiaogang1

1.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Jiangnan University,Wuxi,Jiangsu,214122 2.School of Science,Jiangnan University,Wuxi,Jiangsu,214122

From the twin-screw compressor rotor meshing line of view, the meshing line method was introduced in detail, the male and female rotor profiles were deduced from the meshing line by meshing and coordinate transformation relationship. The requirements of continuity were given in the meshing line method and the corresponding solving steps which solved the continuity problems in the meshing line method were carried out. Three critical control points on the meshing line were studied and the impacts of its changes of positions on the rotor profiles generated were summarized, including rotor angles, thicknesses and interdental areas. At last, a profile was designed by the meshing line method, and demonstrates the optimization of new profiles by changing the position of critical control points, the design efficiency is increased.

twin-screw compressor; rotor profile; meshing line method; critical control point

2016-05-24

国家自然科学基金资助项目(51275210，51105175)；江苏省产学研资助项目(BY2013015-30)；江苏省六大人才高峰资助项目(2013-ZBZZ-016)；江南大学自主科研计划资助重点项目(JUSRP51511-5)

TH455

10.3969/j.issn.1004-132X.2017.07.002

何雪明，男，1966年出生。江南大学机械工程学院先进制造中心教授，江苏省食品先进制造装备技术重点实验室副主任。主要研究方向为自由曲线、曲面CAD/CAE/CAM和逆向工程。发表论文50余篇。E-mail:hxuem2003@163.com。姜振钢，男，1991年生。江南大学机械工程学院硕士研究生。武美萍， 女，1970年生。江南大学机械工程学院副院长、 教授、 博士研究生导师。张 荣，女， 1962年生。江南大学理学院副教授。纪小刚，男，1977年生。江南大学机械工程学院副教授。