战术导弹内部分支结构动力学建模

王 亮，周剑波，李 璞，蔡毅鹏，南宫自军

(中国运载火箭技术研究院， 北京100076)

【装备理论与装备技术】

战术导弹内部分支结构动力学建模

王 亮，周剑波，李 璞，蔡毅鹏，南宫自军

(中国运载火箭技术研究院， 北京100076)

基于模型导弹的结构参数，通过有限元方法计算了6种建模方法对应模型的模态，研究了导弹内部分支结构动力学建模的6种方法对全弹模态计算结果的影响。研究发现：考虑分支结构对全弹刚度的影响时，模态计算结果与试验结果较接近；另外细化考虑导弹对分支结构的约束效果时，模态计算结果最接近试验结果。

振动；模态；分支结构

航天工程中，为了对姿态控制设计、动载荷计算、响应分析，以及惯性测量组合的安放位置提供参考，需要精确预示战术导弹的结构动力学特性，而这取决于其精确的动力学模型。设计时，一般采用梁-质量块模型进行导弹结构的动力学建模，而且建模时经常会遇到带内部分支弹性结构的情况，此时如何对内部分支结构进行简化建模，对结构的模态预示的准确度起着决定性的影响。

前人对梁模型做了相当多的研究，通常使用的梁模型包括欧拉梁模型和铁木辛克梁模型[1-3]。前人在使用铁木辛克梁进行精确计算及梁的剪切系数方面进行了较多的研究[4-8]。

另外，在精确分析梁模态方面也进行了大量的研究。王栋[9]研究了梁附带集中质量时系统的横向弯曲自由振动。研究发现集中质量的转动惯性对梁的频率、振型以及灵敏度都有很大的影响。当集中质量的转动惯性较大时，忽略其影响对梁的振动分析可能带来很大的误差。杨亚平[10]分析了集中质量矩阵取代一致质量矩阵后对系统自振频率造成的误差，指出集中质量矩阵应该有条件的使用，根据相对容许误差，给出了实际计算中采用集中质量矩阵时单元尺寸的选取方法。王亮[11]研究了不同梁模型对战术导弹结构动力学特性的影响，给出了3种梁模型，其中包括一种欧拉梁模型和两种铁木辛克梁模型，并与试验数据对比。研究发现，欧拉梁模型在预示导弹低阶模态时，精度较好，但在高阶时不如铁木辛克梁模型，且使用变剪切系数的铁木辛克梁的模型模态预示结果更加接近试验结果。对于类似于等截面悬臂梁的振动系统，刘相[12]分别运用一致质量法和集中质量法进行分析，说明在结构动力响应分析中，集中质量法最主要的优点是节省计算量和计算时间；而采用同样的单元数目时，一致质量法的计算精度相对较高。两种有限单元法分析的结果与精确解进行比较，一致质量法给出的自振频率高于实际值，而集中质量法给出的自振频率低于精确解。由于ANSYS在进行非线性材料的模态分析时并不能很好地处理材料的非线性特性，所以要用ANSYS进行非线性模态分析，必须对该软件自振的计算程序进行修正，张彬彬[13]利用程序先提取非线性静力计算结果中单元的应力大小，然后利用应力大小修正单元的弹性模量，通过这种方式使得材料的非线性特性能被ANSYS模态分析结果反映。

因此，在计算导弹模态时，掌握精确的刚度分布以及质量分布是必需的，若导弹结构内部带有分支梁结构，必须根据分支梁结构的特性以及与全弹之间的约束关系，对分支梁结构进行简化建模。本研究针对这一问题，提出了6种简化建模的方法，通过有限元方法计算对比了6种模型的模态，对比分析了分支结构对全弹模态计算的影响。

1 模型建立

1.1 模态计算理论

模型的振动特征方程为[14]

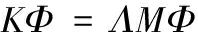
(1)

其中：K、M为结构的刚度、质量矩阵；Λ、Φ分别为结构的特征值与特征向量矩阵。

在计算结构模态时，首先要确定模型的刚度与质量矩阵，而导弹内部的分支梁结构直接影响了全弹的刚度和质量分布。以下通过具体模型研究这种差异。

1.2 模型分析

导弹建模时设计时，一般将弹体简化为梁-质量块模型，并将弹体分为若干个分站，这些分站一般为舱段连接点、仪器放置点，或者某些大型部件的重心，并给出弹体的各分站处的集中质量以及各分站之间梁的材料和截面尺寸。

如图1所示，某型导弹采用梁动力学模型。每个节点为一分站，从节点1到36为导弹主梁节点，在节点8～14区域内，导弹内部有一个分支梁结构，并以8、10和13为连接截面，其中10为主支撑结构，连接刚度较强，8和13为辅助支撑结构，8站支撑结构为一种托盘状的连接，13为径向支架连接，刚度均较弱。

图1 导弹分站模型

1) 质量单元

分站质量与转动惯量添加在对应的自由度方向，对应分站的转动惯量计算公式[14]为

(2)

其中：me为该站上的集中质量；R为该站处的弹体半径；h为处于端点时取它与相邻点间距之半；处于中间点时取它相邻的前后两点间距之半。

2) 刚度单元

由于弹身为连续气动外形，因此各节点处截面半径不相等，因此采用变截面梁单元技术，使用型函数导数与材料参数矩阵乘积在单元长度上积分的方法，得到各单元的刚度矩阵，具有变剪切系数k的铁木辛克梁模型。

考虑剪切后，单元上任意一点的转角为

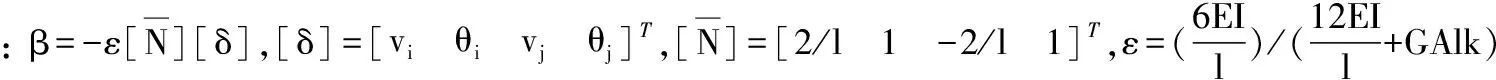
变截面梁单元的刚度计算公式[11]如式(3)所示。

单元的刚度矩阵为

(3)

根据弹性力学中的定义，截面的剪切系数与其面上的剪切应力的分布有关，剪切系数k的计算公式[8]为

(4)

其中：A为截面面积；Q为截面所受的剪力；τxy和τxz是剪力Q引起的截面分布剪应力。

要给定某一截面的剪切系数，必须先对剪应力的分布做一定假设。最简单的假定剪应力的分布与材料力学相同，但是这样导致剪应力与实际分布相差较大，求出的剪切系数与真实情况相差较大。本研究中，假设剪应力的分布与弹性力学中悬臂梁的剪应力分布相同，将公式(4)积分可以得到截面内外径比为m的薄壁圆管截面剪切系数计算公式[15]为

(5)

1.3 简化模型

针对导弹内部的分支梁结构，本文研究了6种简化模型:

模型一：集中质量模型。由于主支撑刚度较强，将分支梁结构的质量以给出的集中质量形式连接在梁主支撑分站位置；

模型二：分支梁刚度模型1。考虑分支梁的刚度，其以分支梁结构通过连接节点与主梁连接及分支梁与主梁在连接位置共用节点，共用平动和转动自由度。

模型三：分支梁刚度模型2。在模型二的基础上，考虑分支梁与主梁的连接关系，定义主支撑和前辅助支撑共用平动和转动自由度，而后辅助支撑仅为径向支架连接，因此仅共用平动自由度。

模型四：分支梁刚度模型3。考虑分支梁与主梁的连接关系，定义主支撑共用平动和转动自由度，而后辅助支撑仅共用平动自由度；

模型五：分支梁刚度模型4。考虑分支梁与主梁的连接关系，定义主支撑和后辅助支撑均共用平动和转动自由度。

模型六：分支梁刚度模型5。考虑分支梁与主梁的连接关系，定义主支撑和前辅助支撑均共用平动和转动自由度。

从以上6种模型可以发现，模型一为仅考虑分支结构的质量特性，未考虑其对全弹的刚度贡献，模型二考虑了分支结构的质量和刚度，但未细化考虑分支结构与全弹结构的刚度贡献，模型三在模型二的基础上，考虑了分支结构与全弹的约束作用，细化了其对全弹结构的刚度影响，模型四和模型五与模型二和三为未考虑前辅助支撑的刚度贡献，模型六为模型二和三未考虑后辅助支撑的刚度贡献。

以下针对提出的6种模型，进行算例分析，研究不同的建模方法对全弹模态的影响。

2 算例

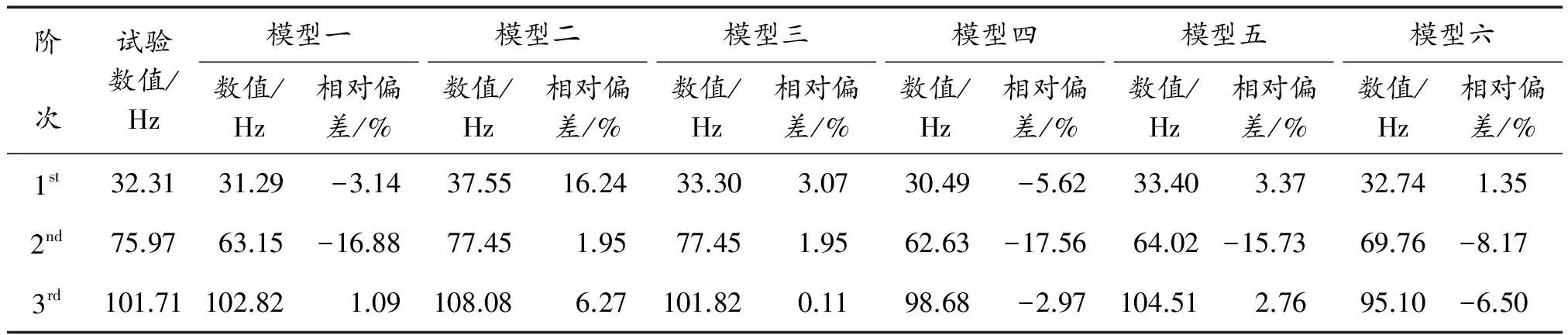
根据相关参数，分别使用上节给出的各种模型计算结构的模态。图2～图4分别比较了各种模型与试验结果的前三阶归一化的模态振型。表1给出了各种模型的前三阶模态频率和试验结果的对比。

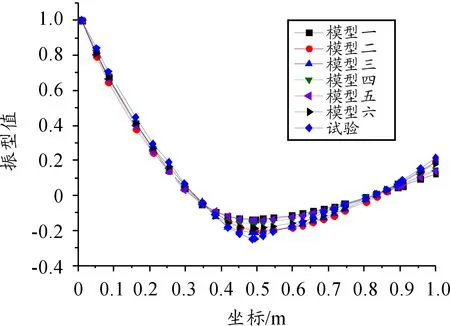
图2 各种模型的第一阶归一化的固有振型对比

图3 各种模型的第二阶归一化的固有振型对比

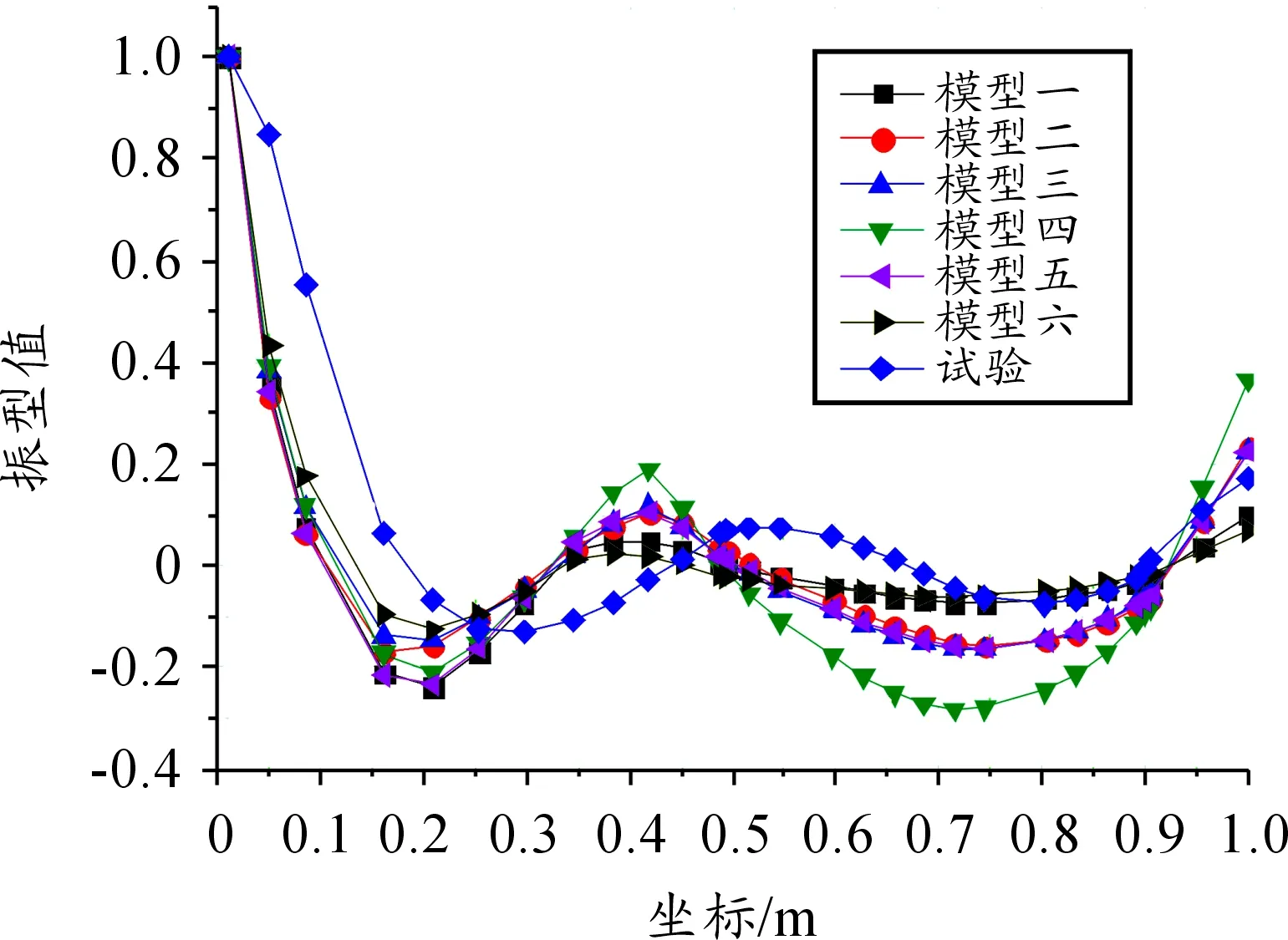
图4 各种模型的第三阶归一化的固有振型对比

阶次试验数值/Hz模型一数值/Hz相对偏差/%模型二数值/Hz相对偏差/%模型三数值/Hz相对偏差/%模型四数值/Hz相对偏差/%模型五数值/Hz相对偏差/%模型六数值/Hz相对偏差/%1st32．3131．29-3．1437．5516．2433．303．0730．49-5．6233．403．3732．741．352nd75．9763．15-16．8877．451．9577．451．9562．63-17．5664．02-15．7369．76-8．173rd101．71102．821．09108．086．27101．820．1198．68-2．97104．512．7695．10-6．50

从以上计算结果可以发现：

1) 从6种模型的前三阶振型图看出，模型二和模型三的模态振型与试验结果较为一致，尤其是前两阶，模型一、四、五和六的模态振型与试验结果差异较大，其中模型一差异最大；

2) 从6种模型计算的模态频率结果对比，发现模型三的前三阶模态频率结果与试验结果最接近，且最大偏差在3%左右，而模型一、四、五和六的第一和第三阶模态频率与试验结果较接近，第二阶偏差较大，其中模型六的偏差最小，模型二的第二阶模态频率与试验结果较接近，第一阶与第三阶偏差较大。

3) 从计算结果看出，分支结构的刚度对全弹模态的第三阶影响较小，而细化考虑分支结构与全弹的约束关系提高了全弹第一阶模态的预示精度，另外3个支撑的刚度均需要细化考虑，单独考虑单个辅助支撑的作用均会造成预示模态不准确。

比较计算结果发现，模型三的分支梁简化方法最接近实际情况，分支梁对各阶全弹模态的影响较大。

3 结论

1) 考虑分支结构对全弹刚度的影响时，模态计算结果与试验结果较接近；另外细化考虑导弹对分支结构的约束效果时，模态计算结果最接近试验结果。

2) 考虑分支梁刚度建模和分支梁与全弹约束关系时，即模型三的分支梁简化方法最接近实际情况，分支梁对各阶全弹模态的影响较大。

[1] CLEGHORN W L,TABARROK B.Finite element formulation of a tapered Timoshenko beam for free vibration analysis[J].Journal of Sound and Vibration,1992,152(3):461-470.

[2] AL-GAHTANI H J.Exact stiffness for tapered members[J].Journal of Structural Engineering,1996,122(10):1234-1239.

[3] 陆念力,张宏生.计及二阶效应的一种变截面梁精确单元刚度阵[J].工程力学,2008,25(12):60-64.

[4] 周世军，朱晞.一组新的Timoshenko梁单元一致矩阵公式[J].兰州铁道学院学报，1994,13(2):1-7.

[5] 李华,武兰河,黄 羚.一种新的考虑剪切变形影响的梁单元[J].石家庄铁道学院学报,1999,12(4):58-61.

[6] 刘文炼.一种新的Timoshenko梁单元[J].广东土木与建筑,2007(12):13-14.

[7] 胡海昌.弹性力学的变分原理及其应用[M].北京:科学出版社,1981:144-147.

[8] 王乐,王亮.一种新的计算Timoshenko梁截面剪切系数的方法[J].应用数学和力学,2013,34(7):756-763.

[9] 王栋,附带有考虑集中质量的转动惯性的梁固有振动分析[J].振动与冲击,2010,29(11):221-225.

[10]杨亚平,沈海宁.集中质量矩阵替代一致质量矩阵的合理性生与局限性[J].青海大学学报:自然科学版,2010,28(1):35-39.

[11]王亮,商霖,王乐.战术导弹结构动力学建模研究[J].战术导弹技术,2013(1):24-27.

[12]刘相.一致质量含参和集中质量含参的比较分析[J].辽东学院学报:自然科学版,2010,17(3):207-210.

[13]张彬彬,朱瑜林,王海城.考虑材料非线性的预应力梁模态分析[J].工程质量,2016,34(1):33-37.

[14]尹云玉.固体火箭载荷设计基础[M].北京:中国宇航出版社,2007.

[15]胡海昌.弹性力学的变分原理及其应用[M].北京:科学出版社,1981:144-147.

(责任编辑 周江川)

Study on the Structure Dynamic Modeling of Tactical Missile with Internal Branches

WANG Liang, ZHOU Jian-bo, LI Pu, CAI Yi-peng, NANGONG Zi-jun

(China Academy of Launch Vehicle Technology, Beijing 100076, China)

Based on the real parameter of the rocket, the modes for the six models were simulated by FEM method to analyze the influence of the six models on the rocket’s modes. It is found that the model are more closed to the experimental results when the branches are modeled, and the model are most close, considering the constraining relationship between the branches and the rocket.

vibration; mode; structures with branches

2016-10-08；

2016-12-25 基金项目：国家重点实验室2015年开放课题(MCMS-0115G01)；国防技术基础科研项目(JSZL2015203B002)

王亮(1985—)，男，博士，高级工程师，主要从事导弹载荷与环境设计研究。

10.11809/scbgxb2017.05.004

format:WANG Liang, ZHOU Jian-bo, LI Pu, et al.Study on the Structure Dynamic Modeling of Tactical Missile with Internal Branches[J].Journal of Ordnance Equipment Engineering,2017(5):18-21.

TJ761.1

A

2096-2304(2017)05-0018-04

本文引用格式：王亮，周剑波，李璞，等.战术导弹内部分支结构动力学建模[J].兵器装备工程学报，2017(5):18-21.