等弧厚七孔发射药抛放弹内弹道计算

李海军，游 坤，莫子烯

(海军航空工程学院 兵器科学与技术系， 山东 烟台 264001)

【装备理论与装备技术】

等弧厚七孔发射药抛放弹内弹道计算

李海军，游 坤，莫子烯

(海军航空工程学院 兵器科学与技术系， 山东 烟台 264001)

航空抛放弹内弹道计算通常使用的是形状函数法，具有严格的推导过程，但是当发射药分裂后，二项式函数不能完全体现发射药的形状特征。针对该问题，根据火药几何燃烧定律，通过计算七孔发射药瞬时燃烧面积，提出了等弧厚七孔发射药的内弹道新算法，可以满足当发射药完全燃烧时,相对燃烧面积是零,提高内弹道计算精度。

抛放弹；七孔发射药；瞬时燃烧面积；内弹道本文引用格式：李海军，游坤，莫子烯.等弧厚七孔发射药抛放弹内弹道计算[J].兵器装备工程学报，2017(5):14-17.

我国机载武器弹射装置主要是热弹射装置[1]，以航空抛放弹燃烧产生的高压高温气体作为动力源，将化学能转化为动能，发射药的燃烧过程是内弹道计算、分析的基础。现代战争中，为了能满足更多的运用领域和使用要求，发射药的形状已经变得纷繁多样，出现了管状药，多孔药，花边形火药等[2-4]。火药形状的改变，对于提高内弹道性能、点火可靠性等都有好处。而目前抛放弹内弹道计算主要使用的是形状函数法，七孔火药分为增面燃烧阶段和减面燃烧阶段，减面燃烧阶段使用形状函数法不能完全体现发射药分裂后的形状特点[5-6]。

本研究在经典内弹道学基础上，以等弧厚七孔发射药为例，通过计算发射药任意瞬时的燃烧面积和燃气生成速率，得出抛放弹燃烧内弹道特性[7-8]。

1 抛放弹内弹道方程组

本研究中的抛放弹模型内部发射药是等弧厚七孔黑火药，其燃烧过程复杂，涉及化学，气体动力学等因素[9]，经过前人大量实验，最终以火药燃气生成速率反映抛放弹内弹道特征。为简化实际工程计算过程，现作如下假设[10-11]：

1) 在额定点火压力下，发射药瞬时完全燃烧，其燃烧过程满足几何燃烧定律。

2) 燃烧室内的高压燃气压强大于20 MPa，但是为了简化计算，近似按理想气体处理[11]。

3) 发射药燃烧线速度取指数函数形式。

4) 燃烧室散热量计算复杂，采用修正系数修正。

5) 高温燃气的成分以及其物理、化学性质看作固定不变，发射药燃烧时，燃气温度瞬时达到峰值，视作常量[12]。

根据以上5点假设，由于燃烧过程满足几何燃烧定律，故可取一粒发射药进行计算，七孔发射药物理模型如图1。根据经典内弹道理论，可以得出以下方程组。

图1 七孔发射药物理模型

根据质量守恒方程，燃烧室剩余气体质量等于已经燃烧的火药质量减去流出燃烧室的燃气质量：

(1)

燃速定律方程：

(2)

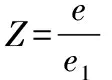
(3)

由喷口流出的燃气质量m1与燃烧室压强P有关，燃烧室压强绝大多数时间高于低压室压强，可分段进行计算。

(4)

当pd≤βp，

(5)

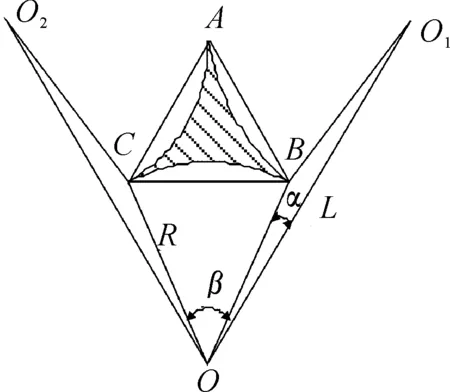
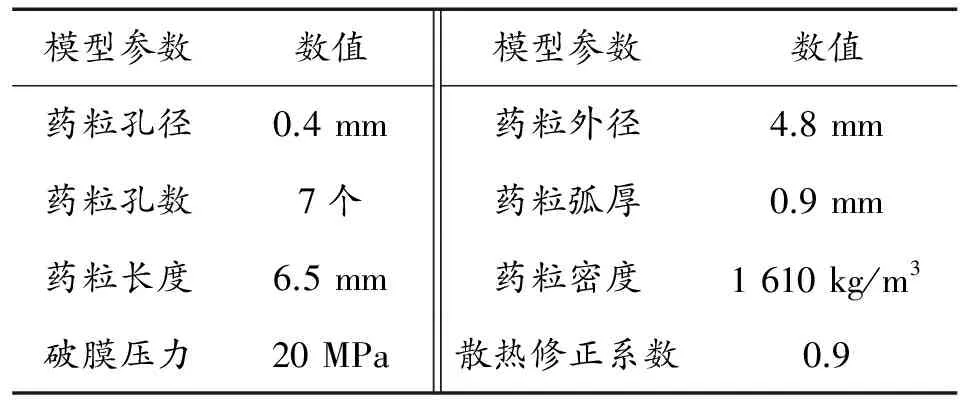
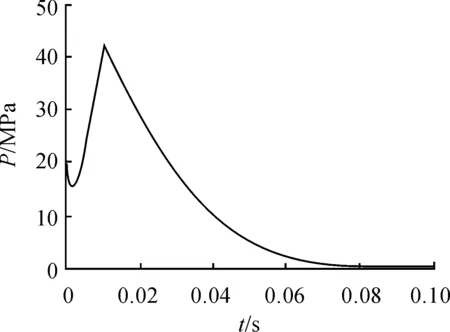
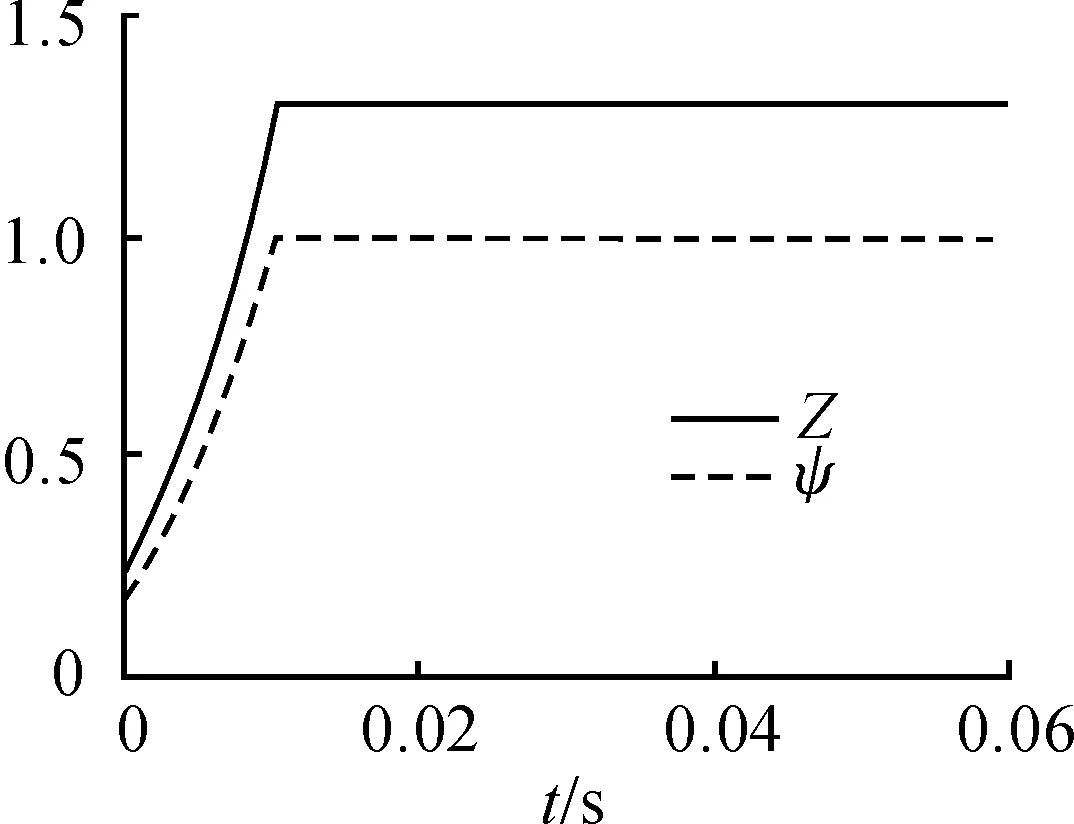
当βp

(6)

(7)

(8)

由气体状态方程P=ρRT以及火药气体比容ω的定义，可以推导P-t微分方程：

(9)

其中，燃烧室自由容积等于：

(10)

燃气生成速率公式：

(11)

式中：P是燃烧室压强；e是某瞬时已经燃烧的火药厚度；2e1是火药起始厚度；u是燃速系数；u1是燃烧室流量系数；n是燃速指数；Z是火药燃去的相对厚度；m是火药初始质量；m1是流出燃烧室气体质量；ψ是火药燃去百分比；Vt是燃烧室内自由容积；V0是燃烧室的初始容积；Gf是单位时间流出喷口的燃气质量；ρ是燃烧室燃气密度；ρ1是火药单体密度；χ1是散热修正系数；S是喷口截面积；s是发射药某瞬时的燃烧表面积；k是绝热指数。

在上述方程组中，由式(3)、式(9)、式(11)可得，3个方程有4个未知数Z、ψ、P、s，即需要表示出火药瞬时燃烧表面积s，就可以得出发射药燃烧时的P-t曲线。

2 七孔火药瞬时燃烧表面积

等弧厚七孔火药燃烧遵循几何燃烧定律，所有表面同时燃烧[2]，分裂前，属于增面燃烧，相对燃烧面积不断增加，分裂后形成6个体积较小的端面为曲边三角形的柱体和6个体积较大的端面也为曲边三角形的柱体，变为减面燃烧，相对燃烧面积不断减小。分裂后小柱体物理模型如图2，大柱体物理模型如图3所示。

图2 小三角柱体物理模型

图3 大三角柱体物理模型

2.1 分裂前瞬时燃烧表面积

发射药分裂的条件是Z=1，分裂前为增面燃烧，瞬时燃烧面积为火药单体外表面积加上7个孔表面积。

某瞬时t火药单体直径：

Dt=D-2e

(12)

某瞬时t小孔直径：

dt=d+2e

(13)

某瞬时t火药单体长度：

ct=c-2e

(14)

即，某瞬时t时燃烧表面积为：

(15)

2.2 分裂后瞬时燃烧表面积

2.2.1 小柱体燃烧表面积

对于中间6个小柱体，取其中一个计算，如图4所示，连接A、B、C，形成等边三角形，连接O、O1、B，形成等腰三角形，瞬时燃烧面积等于3个侧面积加上两个等曲边三角形面积，其中O和O1是小孔的圆心。

图4 小柱体横截面

对任意时刻t小孔半径R：

(16)

两小孔中心矩：

L=2e1+d

(17)

在等腰三角形OO1B中：

(18)

在等腰三角形OBC中：

(19)

曲边三角形ABC中，曲边长度：

(20)

AC边长度：

(21)

等边三角形ABC面积：

(22)

弓形AC面积：

(23)

即，小柱体任意时刻t燃烧面积为侧面面积加上两端面积：

s3=6(3l1(c-2e)+2(s1-3s2))

(24)

2.2.2 大柱体燃烧表面积

对于6个大柱体，横截面如图5，用直线连接各点，燃烧面积为三个侧面积加上两个截面积，而截面积等于等腰三角形ABC的面积加上弓形AB的面积，减去弓形AC，BC的面积，OO1O2构成等边三角形。

图5 大柱体横截面

同理，小孔瞬时半径：

(25)

两小孔中心矩：

L=2e1+d

(26)

在等腰三角形O1O2C中：

(27)

在三角形O1OB中，根据三角形余弦定律可得：

(28)

(29)

即：

(30)

内弧BC长度：

(31)

外弧AB长度：

(32)

大柱体侧面面积：

(33)

弓形AC面积：

(34)

弓形AB面积：

(35)

对于等腰三角形ABC面积：

(36)

柱体两横截面面积：

(37)

即，大柱体任意时刻t燃烧面积：

s9=s4+s8

(38)

综上所述，等弧厚七孔发射药燃气生成速率分段表达式如下，其中Z1是小柱体燃尽时的相对燃烧厚度。

当Z≤1

(39)

当1

(40)

当Z>Z1

(41)

上述主要对发射药燃气生成速率进行了数学建模，得到了七孔发射药不同燃烧阶段燃气生成速率算法。

3 仿真计算

使用本文推导的瞬时燃烧面积计算模型，计算发射药的燃气生成速率，计算航空抛放弹内弹道特性。本模型使用的发射药是某黑火药，此发射药的主要计算参数如表1所示。

表1 主要计算参数

根据微分方程式(3)、式(9)、式(11)，调用Matlab软件中“ODE45”解微分方程，其精度高，收敛迅速。得出燃烧室的压强变化曲线如图6，得出发射药的已燃相对厚度Z和已燃相对体积ψ随时间变化曲线如图7所示。

图6 燃烧室压强变化曲线

图7 已燃相对厚度、体积变化曲线

由图6可以看出，发射药的破膜压强是20 MPa，破膜瞬间，气体流出，燃烧室压强在短时间内略有降低，随着发射药继续燃烧，燃烧室内压强迅速升高，在12 ms时压强达到峰值42 MPa，小于此抛放弹设计的最大压强，仿真结果满足设计要求。压强曲线没有明显的平衡阶段，因为此发射药燃烧分为增面燃烧和减面燃烧，在增面燃烧时，它的平衡曲线是上升曲线，而减面燃烧的平衡曲线是下降曲线。

由图7可以看出，在12 ms时，发射药已燃相对厚度和已燃相对体积不再发生变化，此时火药完全燃烧，ψ是1，而此时Z是1.38，不再增加。保证了火药完全燃烧时，火药的瞬时燃烧面积是0。当Z为1时，发射药分裂，此时已燃相对体积是0.78。

4 结论

发射药燃气生成速率能直接反映其内弹道特性，可以通过控制燃气生成速率达到控制压强大小的目的。本文通过计算发射药任意时刻的燃烧面积，提出了计算燃气生成速率的新算法。结合质量守恒方程，气体状态方程，流量方程，燃速方程等，计算抛放弹燃烧内弹道特性，得出的内弹道仿真结果符合我国“军标”规定的要求，证明此算法可行。没有进行真实实验，理论仿真和实际结果必然会有偏差。

[1] 甄建斌，徐诚，王涛.某机载导弹弹射系统动态仿真及其性能分析[J].南京理工大学学报，2012，36(1)：142-146.

[2] 刘树花，曹锋.多孔火药燃烧分裂后药粒的形状函数计算研究[J].火炮发射与控制学报，2003，16(2)：33-36.

[3] 柴俊，马忠亮.七孔变燃速发射药挤出胀大的模拟[J].四川兵工学报，2015，36(4)：124-126.

[4] 王亮，许厚谦，薛锐.基于内弹道过程的膛内燃烧产物的计算[J].弹道学报，2014，26(1)：13-16.

[5] 魏志芳，陈国光.火药燃烧性能的矢量计算方法[J].弹箭与制导学报，2005，25(1)：164-167.

[6] 王颖泽,张小兵,袁亚雄,等.多孔火药温度场计算及热应力分析[J].南京理工大学学报(自然科学版)，2008，32(5)：531-535.

[7] 王泽山.控制发射装药燃气生成规律的一种方法[J].华北工学院学报，2001，22(4)：252-255.

[8] 杨敏涛，张向明.多孔火药内外弧厚不等对内弹道性能的影响[J].弹道学报，2004，16(2)：15-18.

[9] 马忠亮,王率宇,刘平.七孔变燃速发射药参数对燃烧性能影响的研究[J].化工新型材料，2016，44(9)：72-75.

[10]程山，马忠亮，代淑兰，等.七孔变燃速发射药内弹道性能的数值计算[J].火炸药学报，2014，37(2):78-81.

[11]袁曾凤.火箭导弹弹射内弹道学[M].北京：北京工业学院出版社，1987.

[12]鲍延玉.内弹道学[M].北京：北京理工大学出版社，1995.

(责任编辑 周江川)

Interior Ballistic Calculation of Cartridge with Equal Web Size Seven-Perforation Gun Propellant

LI Hai-jun， YOU Kun， MO Zi-xi

(Department of Armament Science and Technology, Naval Aeronautical University, Yantai 264001, China)

The shape function method is usually used in interior ballistic calculation of aviation cartridge. It has a strict derivation process, but when gun propellant splits, the binomial function cannot fully reflect the shape characteristics of gun propellant. According to the geometric combustion law of gunpowder, a new calculation method of interior ballistic for equal web size seven-perforation gun propellant is proposed by calculating seven-perforation gun propellant instantaneous combustion area, which can meet that when the gunpowder completely burned, the relative burning area is zero, and it can improve the accuracy of interior ballistic calculation.

cartridge; seven-perforation gun propellant; instantaneous combustion area; interior ballistic

2016-12-30；

2017-01-26 作者简介：李海军(1966—)，男，博士，教授，博士生导师，主要从事航空导弹测试与故障诊断研究。

10.11809/scbgxb2017.05.003

format:LI Hai-jun，YOU Kun，MO Zi-xi.Interior Ballistic Calculation of Cartridge with Equal Web Size Seven-Perforation Gun Propellant[J].Journal of Ordnance Equipment Engineering,2017(5):14-17.

TJ765.239

A

2096-2304(2017)05-0014-04