蒸汽发生器安全端焊接接头应力强度因子计算

朱保印，夏晓舟，何 铮，顾水涛，裴 磊

(1.河海大学力学与材料学院,江苏 南京 210000； 2.国核华清(北京)核电技术研发中心有限公司，北京 100084)

蒸汽发生器安全端焊接接头应力强度因子计算

朱保印1，夏晓舟1，何 铮2，顾水涛1，裴 磊1

(1.河海大学力学与材料学院,江苏 南京 210000； 2.国核华清(北京)核电技术研发中心有限公司，北京 100084)

推导含初始应力场的扩展有限元(XFEM)弱形式，并应用到焊接导致的残余应力场下裂纹问题数值模拟中。采用互作用积分策略以获得更精确的计算应力强度因子(SIF)。在此基础上，分析蒸汽发生器(SG)安全端异种金属接头在焊接残余应力场下SIF随裂纹深度的变化情况。研究发现，随着焊接接头内侧裂纹的不断深入，SIF先增大、后减小，这表明材料对裂纹扩展的抗力是先增大、后减小的过程。初始应力场施加方法利用了XFEM在模拟裂纹扩展上的优势，避免了网格更新导致的重复计算。

蒸汽发生器；XFEM；互作用积分；SIF；焊接残余应力场

图1 SG安全端示意图Fig.1 Sketch of steam generator (SG) safety side

焊接是核电站建造与安装的关键工艺。压水堆(PWR)蒸汽发生器(SG)安全端异种焊接接头这种特殊的焊接结构，是核电安全运行的关键部件。核电站现场运行经验表明，焊接接头以应力腐蚀开裂(SCC)为代表的环境致裂(EAC)是PWR一回路的主要环境损伤现象，已成为影响核电站长期安全运行的关键问题之一。焊接残余应力是引起应力腐蚀开裂的主要原因。准确模拟焊接残余应力场下裂尖应力状态并计算SIF是SG安全端结构的完整性评价和寿命预测中[1-3]的关键问题。目前，国内外学者已经提出了很多计算裂纹扩展的方法[4]，如边界元法[5]、无网格方法[6]、有限元网格更新法[7]等，这些方法在求解裂纹扩展问题时都有良好的表现。基于有限元的网格更新法虽然适应性强，但是针对焊接残余应力场下SG安全端(图1)内侧不同深度裂纹模拟这一问题，采用常规FEM处理，随着裂纹的扩展需要不断更新裂纹周围的网格，在处理焊接残余应力场下裂纹问题时工作量大，计算效率较低。扩展有限元(XFEM)[8-9]基于传统有限元方法，克服了网格更新方法的缺点，通过扩充位移项来描述不连续的位移场模拟裂纹问题，减少了工作量。SIF数值计算方法常用的方法有应力外推法、J积分法等，采用J积分法计算SIF精度较高[10]。

本文推导考虑初始应力的XFEM方法，分析J积分求解SIF的求解精度，并结合工程实例，分析了核电某安全端异种金属焊接接头在焊接残余应力场下裂尖SIF。

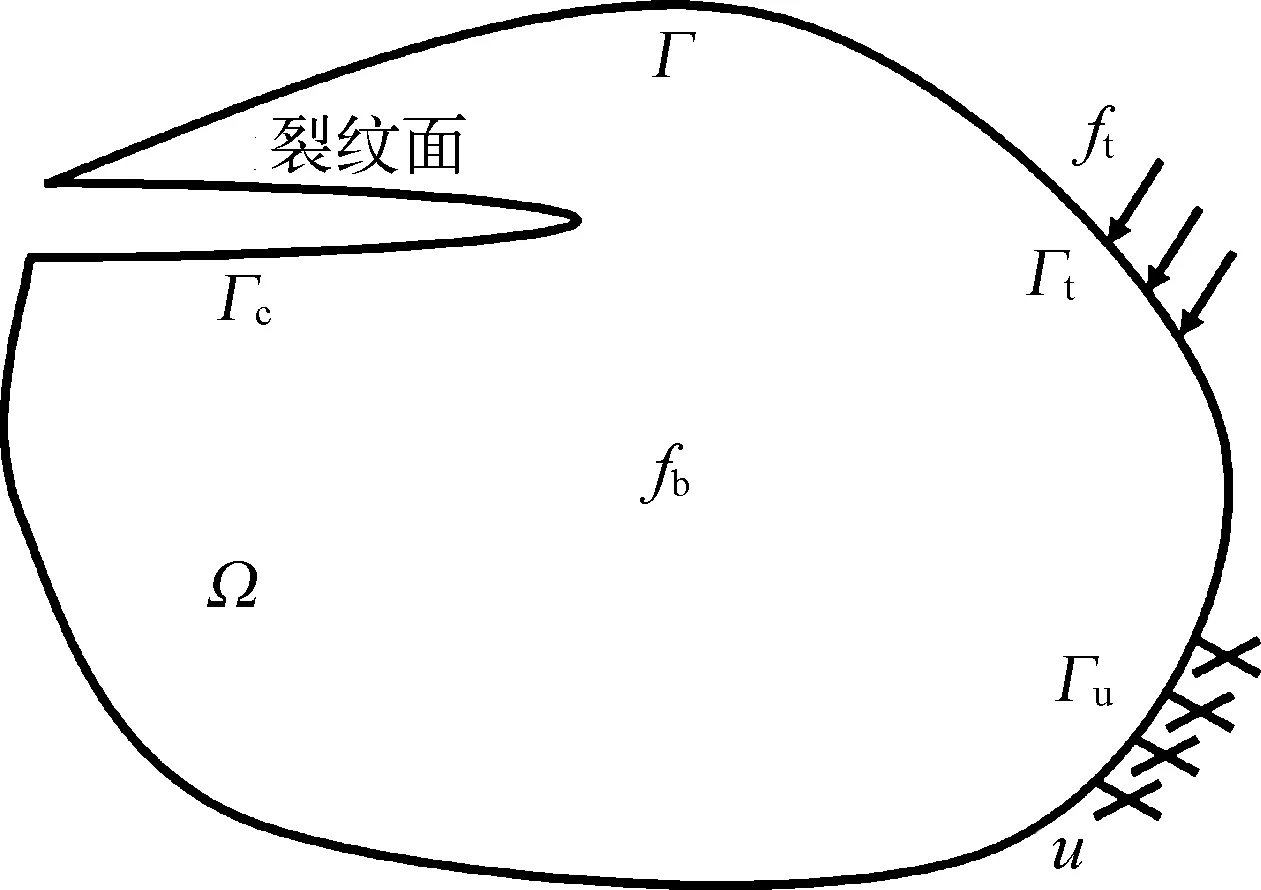
图2 各向同性弹性体受力情况Fig.2 Force diagram of isotropic elastostatic body

1 扩展有限元理论方法

1.1 控制方程

考察弹性静力平衡体Ω，受外力和体力作用的各向同性弹性体受力如图2所示，边界条件为Γ，其中，力边界为Γt、位移边界为Γu、裂纹面边界为Γc，变形体平衡方程弱形式可写为

(1)

考虑初始应力的平衡方程弱形式可离散为

(2)

式中：N——插值函数矩阵；B——应变矩阵；D——弹性矩阵；ue——单元位移向量；Ωe——积分单元；Γt,e——积分单元力边界。

1.2 XFEM位移逼近

SG安全端为异种金属焊接接头，XFEM位移逼近由4部分组成[11-12]： 常规有限元结点位移uN、裂纹切割结点加强位移uH、裂尖结点加强位移utip和弱不连续结点加强位移umat。

u(x)=uN(x)+uH(x)+utip(x)+umat(x)

(3)

2 应力强度因子求解

SIF是表征裂纹裂尖场的重要物理参数。张开型(Ⅰ型)裂纹的SIF为KⅠ，剪切型(Ⅱ型)裂纹的SIF为KⅡ。采用互作用积分方法计算SIF，互作用积分表达式为

(4)

式中，上标aux表示互作用积分中的辅助场。

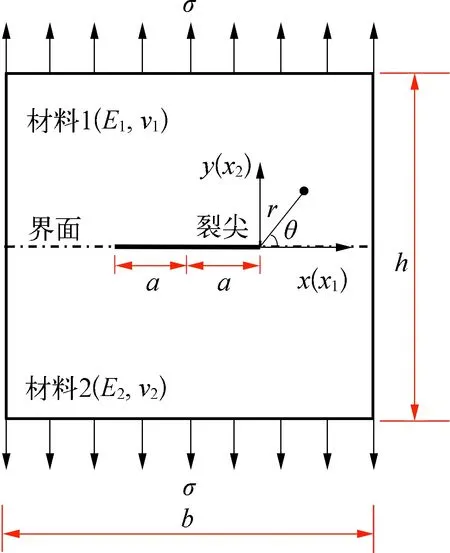
图3 双材料界面裂纹Fig.3 Bimaterial interface crack

对于各向同性材料裂纹，文献[11]给出了平面应力下SIF表达式为

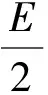
(5)

平面应变情况下为

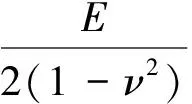
(6)

式中：ν——泊松比；E——杨氏模量。

文献[13]给出了各向同性材料辅助场表达式。

对于双材料界面裂纹(图3)，互作用积分计算SIF的表达式为

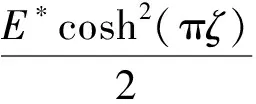
(7)

其中

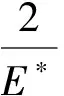
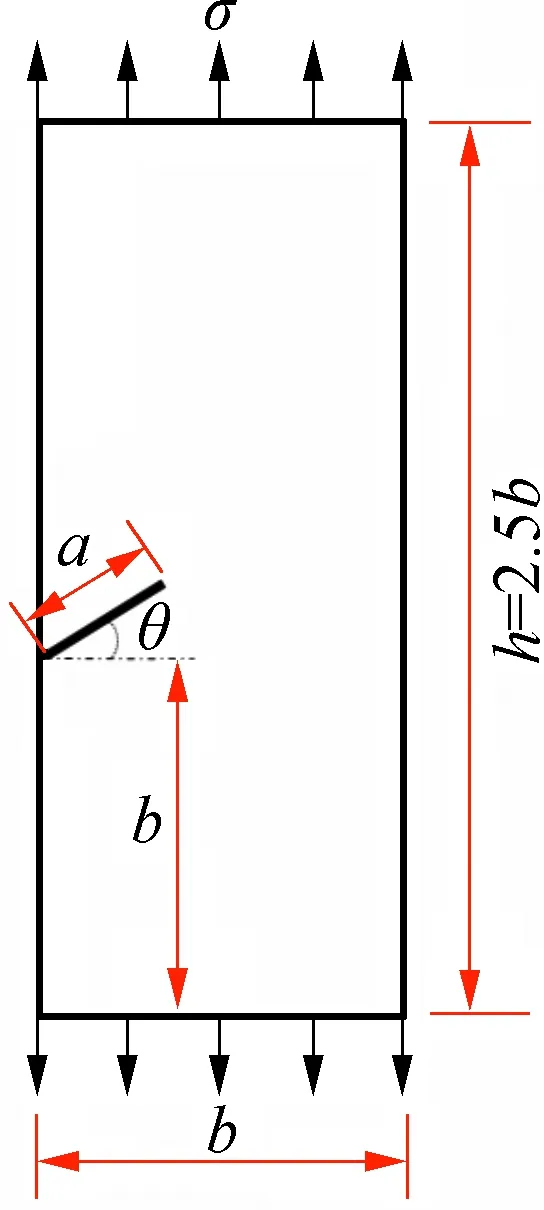
图4 单边斜裂纹Fig.4 Unilateral oblique crack

式中：νj——材料j的泊松比；Ej——材料j的杨氏模量；ζ——裂尖双材料常数[14]；β——第二Dundurs参数[13]。文献[14]给出了双材料界面裂纹的裂尖辅助场。

3 SIF数值验证算例

3.1 有限尺寸板单边裂纹

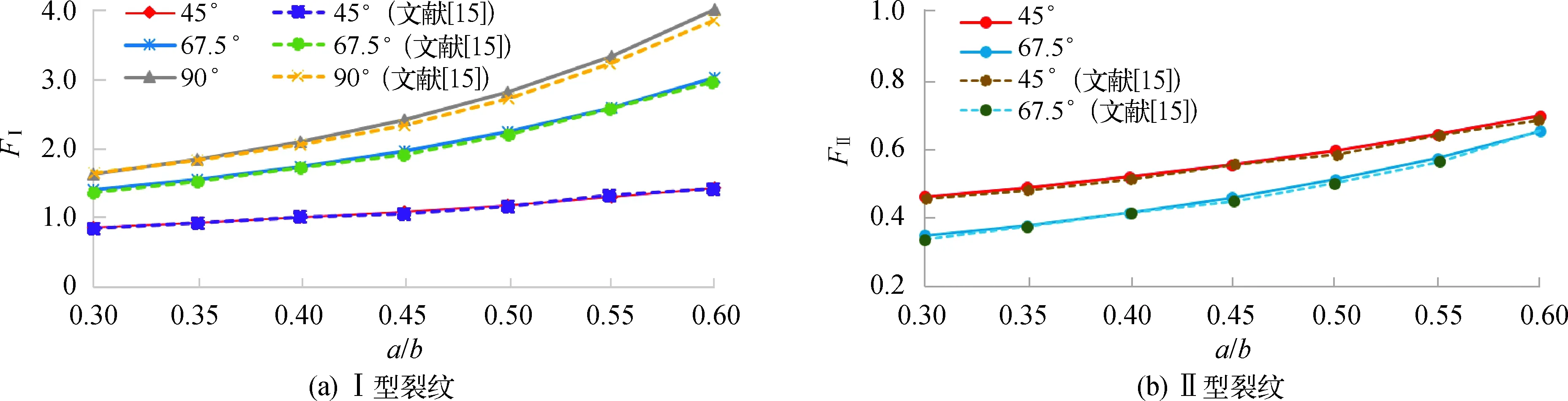
图5 SIF随a/b变化曲线Fig.5 Change of SIF with a/b

3.2 双材料中心界面裂纹

如图3双材料界面裂纹所示，矩形板长h=20 cm，宽b=20 cm，单元数为8 000，荷载为竖向均布荷载σ=1 MPa，裂纹长度为2a=2 cm，裂纹与水平夹角θ。Rice等[16]给出了双材料中心界面裂纹几种情况下的理论解，见表1。由表1可以看出，对于双材料界面裂纹互作用积分同样具有较好的求解精度。

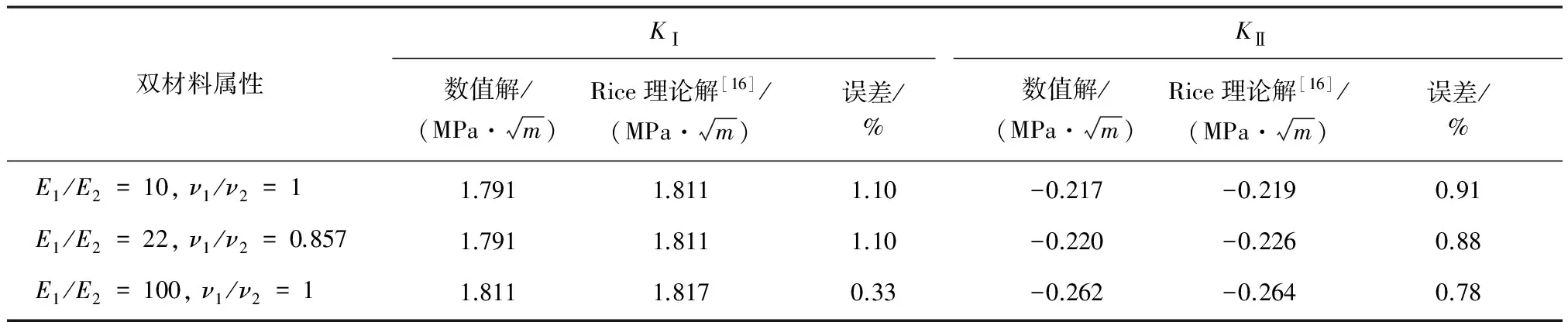
表1 双材料界面裂纹SIF计算与误差

4 焊接残余应力场下SG安全端裂尖应力场分析

SG安全端焊接接头如图1所示，几何构型上模型可简化为一个轴对称问题。采用二维轴对称模型，取管道的一个截面来研究，图1中安全端接管为镍基合金，进口接管为不锈钢，中间红色区域为双U形径向镍基合金堆焊层。正常服役期现场超声波损伤监测显示，安全端焊接接头初始裂纹多为内侧堆焊层区域管道径向裂纹，S22方向拉应力为其裂纹扩展主要影响因素。借助有限元数值模拟，获得复杂的焊接残余应力场如图6所示，从焊接残余应力场分布图可以得出以下几点： (a)应力集中主要位于镍基堆焊层及其热影响区。(b)从S22方向(轴向)应力云图可以看出，S22方向拉应力集中区位于管道内侧和外侧堆焊层区，最大拉应力为422 MPa；S22方向压应力集中区位于管道焊缝中心位置，最大压应力为-417.7 MPa。此外，沿S22方向拉应力有轻微对称，这是由于异种焊材焊接所导致的。

图6 焊接残余应力场应力云图Fig.6 Stress nephogram in welding residual stress field

除焊接残余应力场外，根据SG安全端正常服役环境，本次裂纹模拟考虑了管道内压(17.2 MPa)。

结合焊接残余应力场分布(S22方向)情况，采用XFEM进行裂纹模拟时考虑初始裂纹位于内侧堆焊层中心区(图1)，裂纹长度a考虑以下12组： 5 mm、10 mm、12 mm、20 mm、25 mm、30 mm、35 mm、40 mm、45 mm、50 mm、55 mm和60 mm。

基于XFEM模拟焊接残余应力场下含静态裂纹的SG安全端应力状态，数值模拟结果见图7。采用互作用积分计算SIF可得SIF随裂纹长度变化曲线(图8),其中红色曲线为焊接残余应力场和管道内压共同作用下的SIF随裂纹长度变化曲线，黑色曲线为单独管道内压单独作用下SIF随裂纹长度变化曲线。

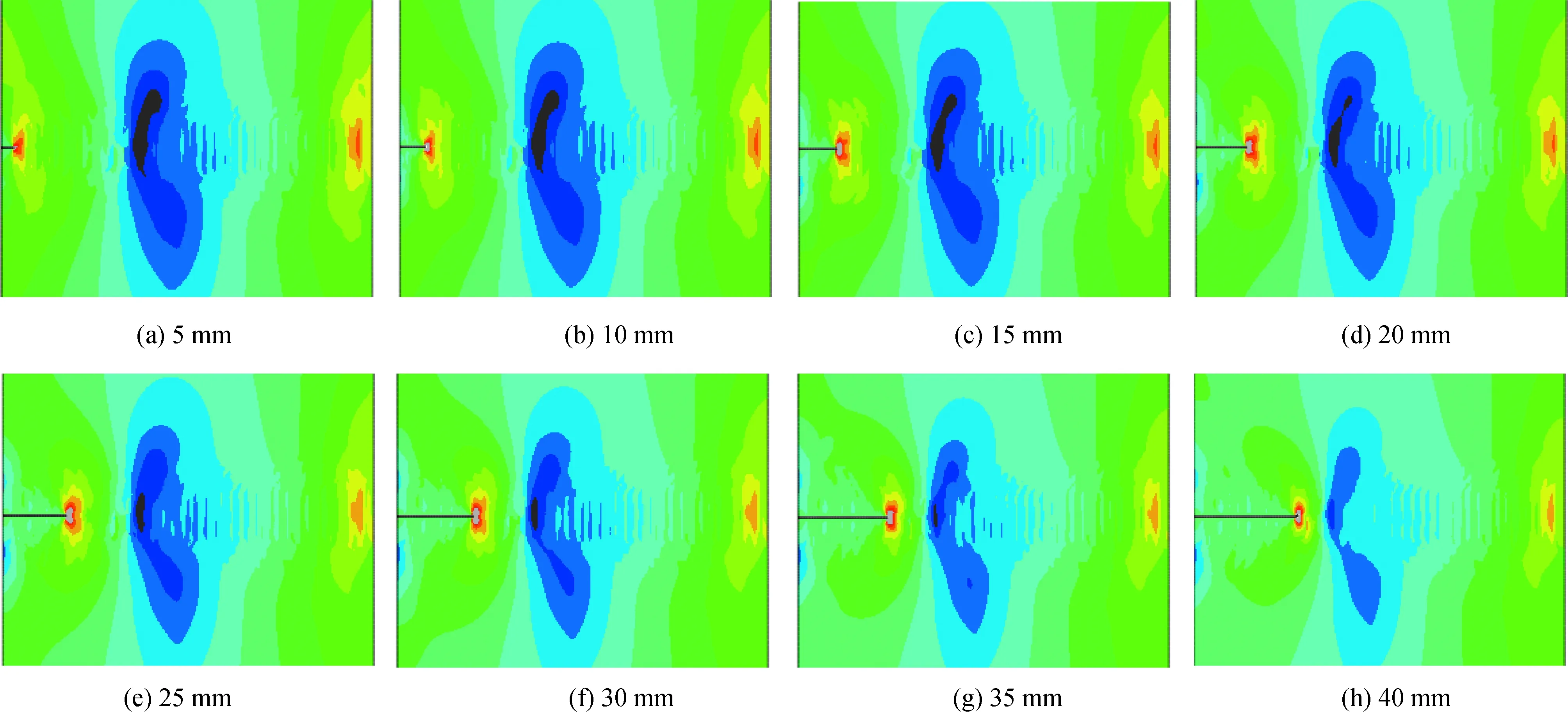
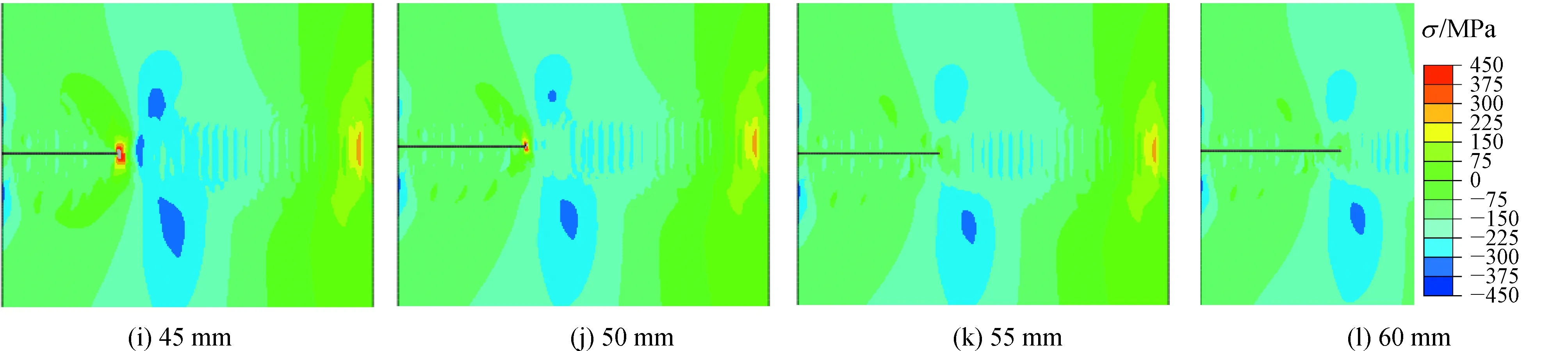
图7 焊接残余应力场下不同长度裂纹应力云图Fig.7 Stress nephogram of cracks with different lengths in welding residual stress field

图8 焊接残余应力场下SIF随裂纹长度变化曲线Fig.8 Change of SIF with crack length in welding residual stress field

从图8可以看出，对于堆焊层中心区裂纹，焊接残余应力场对SIF的影响远大于管道内压对其影响。随着裂纹从SG安全端内侧拉应力区向内部压应力区不断深入，裂尖SIF先增大、后减小，这表明材料对裂纹扩展的抗力是先增大、后减小。

准确获得安全端接头焊接残余应力场下裂纹尖端SIF是SG安全端接头结构完整性评价和寿命预测中的关键环节。借助XFEM模拟裂尖应力场并采用J积分求解裂尖SIF可以有效避免SG安全端焊接模拟和裂纹模拟间的网格不适应问题，并为后续采用基于改进F-A模型[1-3]的适用于核电焊接材料SCC扩展速率预测模型，预测SG安全端剩余服役寿命提供参考。

5 结 语

推导了基于XFEM的初始应力场施加方法。通过与解析解的对比分析，验证了互作用积分计算SIF对于各向同性材料裂纹和双材料界面裂纹具有良好的计算精度。

分析了压水堆SG安全端接头在焊接残余应力场作用下不同裂纹深度的裂尖SIF。研究发现在正常服役工况下，对于堆焊层中心裂纹，焊接残余应力对SG安全端裂尖SIF的影响占主导作用，随着裂纹从SG安全端内侧向内部压应力区不断深入，裂尖SIF是先增大后、减小的过程，即材料对裂纹扩展的抗力是先增大、后减小的过程。研究结果可为后期SG安全端剩余服役寿命评估提供参考。

[1] PETER L Andresen, F Peter Ford. Life prediction by mechanistic modeling and system monitoring of environmental cracking of iron and nickel alloys in aqueous systems[J]. Materials Science and Engineering, 1988, A103(1)： 167-184.

[2] YANG F Q, XUE H. A quantitative prediction model of SCC rate for nuclear structure materials in high temperature water based on crack tip creep strain rate[J]. Nuclear Engineering and Design, 2014, 278： 686-692.

[3] LI Yongkui, YOSHIYUKI K. Effects of thermal load and cooling condition on weld residual stress in a core shroud with numerical simulation[J]. Nuclear Engineering and Design, 2012, 242： 100-107.

[4] 余天堂. 含裂纹体的数值模拟[J]. 岩土力学与工程学报, 2005, 24(24)： 4434-4439. (YU Tiantang. Numerical simulation of a body with cracks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24)： 4434-4439. (in Chinese))

[5] PORTELA A, ALIABADI M H, ROOKE D P. The dual boundary element method： effective implementation for crack problems[J]. International Journal for Numerical Methods in Engineering, 1992, 33(6)： 1269-1287.

[6] BELYTSCHKO T, GU L, LU Y Y. Fracture and crack growth by element free galerkin methods[J]. Mdoelling and Simulation in Materials Science and Engineering, 1994, 2(3A)： 519-534.

[7] BOUCHARD P O, BAY F, CHASTEL Y. Numerical modelling of crack propagation： automatic remeshing and comparison of different criteria[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(35)： 3887-3908.

[8] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(4)： 601-620.

[9] 应宗权, 杜成斌, 程丽. 含夹杂非均质材料的扩展有限元数值模拟[J]. 河海大学学报(自然科学版)，2008, 36(4)： 546-549. (YING Zongquan, DU Chengbin, CHENG Li. Application of extended finite element method in heterogeneous materials with inclusions[J]. Journal of Hohai University(Natural Sciences), 2008, 36(4)： 546-549. (in Chinese))

[10] RU Zhongliang, ZHAO Hongbo, YIN Shunde. Evaluation of mixed-mode stress intensity factors by extended finite element method[J]. Journal of Central South University of Technology, 2013, 20(5)： 1420-1425.

[11] 江守燕, 杜成斌. 弱不连续问题扩展有限元法的数值精度研究[J]. 力学学报, 2012, 44(6)： 1005-1015. (JIANG Shouyan, DU Chengbin. Study on numerical precision of extended finite element method for modeling weak discontinuities[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6)： 1005-1015 (in Chinese)).

[12] CHEN D H. A crack normal to and terminating at a bimaterial interface[J]. Engineering Fracture Mechanics, 1994, 49(4)： 517-532.

[13] DUNDERS J. Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading [J]. Journal of Applied Mechanics, 1969, 36(3)： 650-652.

[14] SUKUMARL N, HUANG Z Y. Partition of unity enrichment for bimaterial interface cracks[J]. International Journal for Numerical Methods in Engineering, 2004, 59(8)： 1075-1102.

[15] 中国航空研究院.应力强度因子手册[M].北京： 科学出版社,1993.

[16] RICE J R, SIH G C. Plane problems of cracks in dissimilar media[J]. Journal of Applied Mechanics, 1965, 32(2)： 418-423.

Calculation of stress intensity factor of steam generator safety-end welded joint

ZHU Baoyin1，XIA Xiaozhou1，HE Zheng2，GU Shuitao1，PEI Lei1

(1.CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing210000,China;2.StateNuclearHuaqing(Beijing)NuclearPowerTechnologyR&DCenterCo.,Ltd.,Beijing100084,China)

The weak form of the extended finite element method (XFEM) with the initial stress field was derived, and was used to numerically simulate the crack in a weld-induced residual stress field. A more accurate stress intensity factor (SIF) was obtained with the interaction integral method. Based on this, the variation of SIF of steam generator safety-end dissimilar metal joints with the crack depth in the weld-induced residual stress field was analyzed. The results show that SIF increases first and then decreases with the continuous propagation of the crack inside the welded joint, indicating that the resistance of a material against crack propagation increases first and then decreases. The method of exerting an initial stress field utilizes the advantage of XFEM in simulation of crack propagation, and avoids the repetitive computation induced by grid updating.

stream generator; XFEM; interaction integral; SIF; welding residual stress field

10.3876/j.issn.1000-1980.2017.03.009

2016-11-25

国家科技重大专项(2012ZX06004-012)

朱保印(1992—)，男，江苏徐州人，硕士研究生，主要从事断裂和扩展有限元算法研究。E-mail： Jusure@outlook.com

顾水涛，副教授。E-mail： gutuozai@hotmail.com

TU122

A

1000-1980(2017)03-0243-06