惠州某区薄储层反演技术研究及应用

梁立锋，张宏兵，刘秀娟，曹呈浩，潘益鑫

(1.河海大学地球科学与工程学院，江苏 南京 210098; 2.中国海洋石油能源发展工程技术特普公司，广东 湛江 524000)

惠州某区薄储层反演技术研究及应用

梁立锋1,2，张宏兵1，刘秀娟2，曹呈浩1，潘益鑫1

(1.河海大学地球科学与工程学院，江苏 南京 210098; 2.中国海洋石油能源发展工程技术特普公司，广东 湛江 524000)

针对惠州某区滚动勘探阶段钻井较少、薄储层预测难度大的问题，采用基于正则化算子的叠前同步反演技术解决钻井偏态分布难以确定砂体横向边界的问题，从而确定更加合理的变程、变差函数等统计学参数，并作为地质统计学反演的关键参数输入；通过开展地质统计学反演，提高薄储层的纵向薄储层识别厚度问题。反演结果表明：预测设计井X3处储层发育，新钻井X3资料验证了此结果；目标区存在A2UP、A2LOW、A2共3套砂体，且互不连通。

惠州；薄储层；正则化；地质统计学反演；变差函数；概率密度函数

惠州某区为已探明含油构造区块，在构造最高点钻探了X1井并获得油气发现，其中A2储层发育且获得油气显示，但砂岩薄互层现象严重。构造高点附近钻探了X2评价井，钻遇砂岩储层A2LOW，储层物性很好，但厚度较薄仅8 m。由于地震资料主频较低，从地震成果剖面上很难分析2口测井A2储层是否连通，并且该区块处于海洋勘探阶段，钻井较少，常规的波阻抗地震反演难以解决薄储层的预测问题。

地质统计学反演是目前较常用的薄储层预测方法，有关地质统计学反演研究的热点之一是如何在地质建模中充分利用地震信息，并完善加入地震约束项的地质统计学建模方法[1-2]。针对开发初期的海上油气田，钻井数量较少，储层非均质性强，融入地震信息约束相比于仅应用测井资料约束的传统建模方法，其反演精度明显提高[3-4]。变差函数作为地质统计学的主要工具，在地质统计学中占有举足轻重的地位，有学者[5-6]深入分析了变异函数的各个参数(步长、容差角度、容差距离)对变异函数(变程、块金值、基台值)的影响；在实践上，地质统计学反演不仅应用于砂泥岩研究，也广泛用于碳酸盐岩等非均质性储层研究[7-8]，并取得了较好的应用效果。地质统计学反演实施前，一般需要进行确定性反演，其目的是调查砂体发育的规模，以便于确定变差变程等参数。目前主流的基于模型的叠前同步反演由于受初始模型影响及反演算法本身的局限性，反演的精度不高[9-10]。

为解决研究区薄储层预测问题，笔者提出了叠前同步反演联合地质统计学反演的策略，并通过实例应用对该方法进行验证。

1 薄储层反演方法

1.1 基于正则化算子的叠前同步反演方法

正则化方法是基于变分原理建立的，其基本思想为：构造正则算子和确定正则参数，并在解空间内使非负泛函(即目标函数)达到最小。正则化方法最重要的是如何构造正则算子和确定正则参数。由于常规正则化方法是在结果上强加一个粗略的惩罚，从而使图像(或模型)全局平滑。然而，一个现实的地质模型不仅假设为由平滑区域组成，而且还被明显的边界(如层界面、断层、不整合、尖灭等)所分隔。这些边界都是模型中非常重要的特征，如何保护这些特征，避免边界过于平滑，是如何有效地使用正则化方法的难点所在。为此，本文提出了正则化叠前同步反演方法，该方法要求势函数为非平方型，其目标函数可以表示为[11-17]

(1)

式(1)中，J1是关于测量模型与数据的某种一致性，当J1取最小值时，一致性或鲜明性变得很好，但解变得不稳定；J2是一个关于解“光滑性”的测量标准，当J2取最小值时，可以获得一个稳定(或光滑)的近似解，J2中势函数的具体形式见文献[2]。λ是用于平衡数据项和先验项之间的相互影响；δ是一种刻度参数，用于在检测的不连续处(或地层界面)调节梯度值。对于先验项，本文强加了一个k阶平滑(k=1,2,3)，当k=1时，先验项求和是在目标点最邻近的水平和垂直方向上所有区域进行；k=2,3分别对应于邻近点之间的梯度矢量(k=2)和Hessian矩阵差分(k=3)。反演时，通过模拟退火算法搜索目标函数J(Z)的全局极小值，以便反演纵波及横波速度、密度等3个参数，其中， R依据Zoeppritz方程求取，W依据测井数据和井旁地震数据由反褶积方法求取，在模拟退火过程中λ逐渐减小，而δ逐渐增大[12]。

1.2 地质统计学反演方法

地质统计学反演采用马尔科夫链蒙特卡洛积分方法(Markov Chain Monte Carlo，MCMC)。MCMC算法所用的思路非常明确：用贝叶斯推论方法构建一个后验概率密度函数(PDF)来表征在已知地质、地震、测井等信息的条件下储层的概率，记做P(储层|地质统计学参数，地震，测井)，然后利用马尔科夫链蒙特卡洛算法对P进行求解，求得近似解函数，从而获得各种所需的油藏属性体[8]。在地质统计学反演中比较关键的是变差函数及PDF。

变差函数一般由变程、块金值、基台值、拱高等参数共同描述，它指的是[5]：假设空间点u只在一维x轴上变化，将区域化变量P在u和u+h处的值之差的方差之半定义为区域化变量P(u)在x轴方向上的变差函数，记为γ=(u,h)，即

(2)

式中：h——距离滞后(或称步长)；E——数学期望；P(u)——在位置u处的变量值；P(u+h)——在位置u偏离h处的变量值。

PDF是利用贝叶斯推断将各种信息源(测井、地震、岩性)的 PDF 函数综合起来求解， PDF的实现过程，详见参考文献[6]，由于上述这些信息可以包含小到几毫秒的地质微层或几微米的岩芯取样，大到绵延几十千米的地质沉积模式，因此它是一个真正意义上的能够综合体现多个变量特征的 PDF。

2 靶区应用实例

靶区惠州某区薄储层发育，且工区内砂岩分布区只有3口钻井(X1～X3)，3口钻井呈不均匀分布，由井资料统计的试验变程不能反映工区的砂体分布。图1为目标靶区典型地震剖面，图中椭圆所示区域为主要目的层。从图1中可以看出，目的层信噪比略低，波形复杂，振幅能量偏弱，加大了反演的难度。

图1 靶区典型地震剖面Fig.1 Typical seismic section in target zone

分别对图1的叠前地震数据做基于模型的叠前同步反演(图2(a))及基于正则化算子的叠前同步反演(图2(b))，并提取了目标砂体的平面图。结合地质沉积规律，通过对比，2种反演方法刻划的砂体边界及砂体细节不同，由此带来了砂体横向变程参数的差异；图2(a)描述的大套砂岩精度较低，难以在地质上给出合理的解释。图2(b)对砂体边界描述的更加合理，由此测量的横向变程参数也更合理。

(a)模型反演 (b)正则化的叠前同步反演图2 基于模型反演和正则化的叠前同步反演的砂体平面图Fig.2 Sand distribution obtained from pre-stack simultaneous inversion based on model and regularization operator

在基于正则化算子反演的基础上进行地质统计学反演，建立了多个等概率的岩性实现数据体。在对多个等概率岩性数据体进行汇总、平均后，结合地震预测岩性概率模型与井点的匹配性分析结果，获得如图3所示的过反演工区3口井的地质统计学预测岩性概率剖面图。

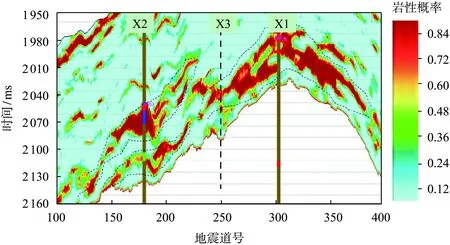
图3 地质统计学反演成果Fig.3 Geostatistical inversion results

从图3可以看出，X1井钻遇A2油藏的砂岩主体部位，该部位砂体纵向厚度大、构造形态处于高部位，砂体在纵向沉积过程中存在相变，实钻结果钻遇3套不同厚度的隔夹层；X2井钻遇的A2油藏砂体在沉积相态上具有岩性沉积特点，该井钻遇A2油藏砂体厚度大，无隔夹层分布，但该砂体向井点外方向呈快速相变(尖灭)特征。

前期的地质综合研究认为，A2砂体与A2UP连通或者A2砂体与A2LOW连通，通过反演研究，A2UP、A2LOW这2套砂体快速相变至尖灭，与A2砂体呈不连续分布，即呈现3套互不连通的砂体结构。新钻井X3井钻遇了A2储层，证实了钻前储层预测结果；由于X3井为含水油层，通过对区域的油气水系统分析，证实了反演所揭示的砂体连通关系，即A2UP、A2LOW、A2存在3套砂体，互不连通。

3 结 论

a.针对钻井数量少且偏态分布情况下的薄储层预测问题，采用基于正则化算子约束的叠前同步反演技术配合地质统计学反演的地震反演策略，提高了统计学反演的精度，储层反演成果获得了新钻井验证。

b.地震反演综合研究认为：目标区存在A2UP、A2LOW、A2共3套砂体，且互不连通，得到了新钻井X3井及区域油气水系统分析结果的支持。

[ 1 ] 王镜惠．地质统计学反演在油藏建模中应用的研究[D].西安:西安石油大学,2012．

[ 2 ] 杨锴，艾迪飞，耿建华．测井、井间地震与地面地震数据联合约束下的地质统计学随机建模方法研究[J]．地球物理学报，2012,55(8):2695-2704.(YANG Kai，AI Difei，GENG Jianhua.A new geostatistical inversion and reservoir modeling technique constrained by well-log，crosshole and surface seismic data [J]．Chinese Journal of Geophysics，2012,55(8):2695-2704.(in Chinese))

[ 3 ] 李绪宣，胡光义，范廷恩，等．基于地震驱动的海上油气田储层地质建模方法[J]．中国海上油气，2011,23(3):143-147.(LI Xuxuan，HU Guangyi，FAN Ting’en，et al．A method of geological reservoir modeling based on seismic drive for offshore fields[J]．China Offshore Oil and Gas,2011,23(3):143-147.(in Chinese)

[ 4 ] 刘振峰．致密砂岩油气藏储层建模技术方案及其应用[J]．地球物理学进展，2014,29(2):815-823.(LIU Zhenfeng．Reservoir modeling program for tight oil & gas sands and its applications[J]．Progress in Geophysics,2014,29(2):815-823.(in Chinese))

[ 5 ] 刘焕荣.实验变异函数及其理论模型的计算与拟合研究[D].云南:昆明理工大学,2014.

[ 6 ] 王海虹.地质统计学在石油勘探开发中的应用[D].黑龙江:东北石油大学,2013.

[ 7 ] 姜文龙，杨锴.岩石物理参数高分辨率地质统计学反演[J].石油物探,2012,51(6):638-648.(JIANG Wenlong,YANG Kai.Petrophysical parameters of high resolution geostatistical inversion [J].Journal of petroleum exploration,2012,51(6):638-648.(in Chinese))

[ 8 ] 韩东，胡向阳，邬兴威,等.基于地质统计学反演的缝洞储集体物性定量评价[J]．地球物理学进展，2016,31(2)：655-661.(HAN Dong，HU Xiangyang，WU Xingwei，et al．Quantitative evaluation for porosity of the fracture-cavity reservoir based on geostatistical inversion[J]．Progress in Geophysics,2016,31(2):655-661.(in Chinese))

[ 9 ] 梁立锋，但志伟，陈剑锋,等.叠前密度反演的误差对含气饱和度估算的影响[J].工程地球物理学报,2011,8(3):257-260.(LIANG Lifeng,DAN Zhiwei,CHEN Jianfeng,et al.The Influence of prestack density inversion error on gas saturation estimate [J].Journal of engineering geophysics,2011,8(3):257-260.(in Chinese))

[10] ARTURO C,CARLOS T V,TIM F.Sensitivity analysis of data-related factors controlling AVA simultaneous inversion of partially stacked seismic amplitude data:Application to deepwater hydrocarbon reservoirs in the central Gulf of Mexico[J].Geophysics,2007,72(1):C19-C29.

[11] ZHANG Hongbing,SHANG Zuoping,YANG Changchun.Estimation of regular parameters for the impedance inversion[J].Chinese Journal of Geophysics,2005,48(1):181-188.

[12] ZHANG Hongbing,SHANG Zuoping,YANG Changchun.A non-linear regularized constrained impedance inversion[J].Geophysical Prospecting,2007,55(6):819-833.

[13] ZHANGHongbing, SHANG Zuoping,YANG Changchun.Adaptive reconstruction method of impedance model with absolute and relative constraints[J].Journal of Applied Geophysics,2009,67(2):114-124.

[14] ZHANG Hongbing,YANG Changchun.A impedance constrained inversion method controlling by regular parameters[J].Chinese Journal of Geophysics,2003,46(6):827-834.

[15] ZHANGJiashu,LYU Songfeng,LIU Yang.AVO inversion based on generalized extreme value distribution with adaptive parameter estimation[J].Journal of Applied Geophysics,2013,98(11):11-20.

[16] ZHANGZhigang,HUANG Lianjie,LIN Youzuo.Double-difference elastic-waveform inversion with prior information for time-lapse monitoring[J].Geophysics,2013,78(6):R259-R273.

[17] YAN Zhe,GU Hanming.Non-linear prestack seismic inversion with global optimization using an edge- preserving smoothing filter[J].Geophysical Prospecting,2013,61(4):747-760.

Thin reservoir inversion technology in an area in Huizhou and its application

LIANG Lifeng1, 2, ZHANG Hongbing1, LIU Xiujuan2, CAO Chenghao1, PAN Yixin1

(1.SchoolofEarthScienceandEngineering,HohaiUniversity,Nanjing210098,China;2.CNOOCEnergyDevelopmentEngineeringGeophysicalProspectingInstituteofTechnology,Zhanjiang524000,China)

In view of fewer drilling wells and the difficulty of thin reservoir prediction in the rolling exploration stage in an area in Huizhou, the pre-stack simultaneous inversion technique based on the regularization operator was adopted to solve the problems of the difficulty of determining the lateral boundary of sand using the skewed distribution of drilling. More reasonable variation and variation functions were determined and treated as the key parameter input for geo-statistics inversion. The predicted thickness of the vertical thin reservoir was improved by geo-statistical inversion. The inversion results show that the reservoir in the design well X3 will develop, and data from the new drilling well X3 verify the result.There are three sets of sand bodies in the target zone: A2UP, A2LOW,and A2, which are mutually unconnected.

Huizhou; thin reservoir; regularization; geo-statistical inversion; variation function; probability density function

10.3876/j.issn.1000-1980.2017.03.007

2016-06-13

国家自然科学基金(41374116)；中国海洋石油总公司科技项目(CNOOC-KJ 125 ZDXM 07 LTD NFGC 2014-04)；中国海洋石油总公司能源发展科技项目(HFKJ-GJ2015001)

梁立锋(1978—)，男，吉林长春人，工程师，博士研究生，主要从事地震资料正反演工作。E-mail：lianglf@cnooc.com.cn

P618.13

A

1000-1980(2017)03-0230-05