基于Copula函数的暴雨潮位组合分析

万永静，刁秀媚，刘 俊，周 宏，栾 慕，李岱远

(1.河海大学水文水资源学院，江苏 南京 210098； 2.江阴市水资源管理办公室，江苏 江阴 214400；3.南京水利科学研究院水文水资源研究所，江苏 南京 210029)

基于Copula函数的暴雨潮位组合分析

万永静1，刁秀媚2，刘 俊1，周 宏1，栾 慕1，李岱远3

(1.河海大学水文水资源学院，江苏 南京 210098； 2.江阴市水资源管理办公室，江苏 江阴 214400；3.南京水利科学研究院水文水资源研究所，江苏 南京 210029)

基于1959—2010年滁河中下游暴雨资料及南京下关站潮位资料，采用Copula函数建立不同重现期下滁河中下游年最大1 d、3 d、7 d暴雨与其相应时间段长江最高潮位的联合分布函数，计算超过某一设计值的暴雨与各个量级潮位、超过某一设计值的潮位与各个量级雨量的遭遇概率。计算结果与南京市城市防洪规划中的结论相近，表明计算方法合理可行，可为暴雨潮位组合计算提供参考。

Copula函数；区间暴雨；长江潮位；组合概率；滁河中下游

近年来，受全球气候变暖影响，各地极端天气频繁出现，伴随着洪水内涝问题的频现，给人们生活带来巨大影响，造成了巨大的财产损失和人员伤亡[1],因此，在城市防洪规划中对水文计算提出了更高的要求。一般城市防洪规划中推求设计洪水的途径主要有两种，一是水位频率曲线直接法，二是由设计暴雨推求设计洪水位的间接法[2]。但在感潮河段，影响设计洪水的水文要素不仅仅是降雨，还需考虑长江潮位顶托影响，进行不同水文要素之间的遭遇组合分析。对于完全独立的水文事件，其联合分布可以简单地用单变量函数相乘得到，但暴雨潮位存在一定的相关性。传统的相关性分析法，当变量相关性不显著时，其使用受到限制。生产实践中常用定性分析法，根据研究区域历年同步观测数据进行简单分析，但不能给出其概率，工程应用中受人为经验影响。Copula函数可以给出水文要素间各种含义的遭遇概率，且其变量的边际分布不受限制。

现代Copula理论形成以来，Copula函数被广泛用来构建联合分布连接函数[3-6]。研究表明，Copula函数能够有效地描述水文事件的内在规律和特征属性之间的相互关系[7-10]。刘曾美等[11]采用Copula函数建立区间暴雨和外江洪水位的联合分布，用以分析排涝风险率和重现期；武传号等[12]基于Copula函数对广州市短历时暴雨与潮位组合分析，建立雨潮组合概率风险模型；郭财秀等[13]利用Copula函数对长江感潮河段上边界流量和下边界潮位进行组合，定量分析不同量级洪潮的组合概率。

本文采用Copula函数建立不同重现期下滁河中下游年最大1 d、3 d、7 d暴雨与其相应时间段长江最高潮位的联合分布，基于联合分布计算超过某一设计值的暴雨与各个量级潮位、超过某一设计值的潮位与各个量级雨量遭遇概率，并将分析结果与相关性分析法计算结果进行对比分析，为感潮河段防洪规划提供科学依据。

1 研究区概况

南京市江北新区位于滁河流域中下游，滁河流域位于江淮之间，系长江下游左岸一级支流。受地理位置、水文气象、地形地貌等因素的影响，滁河中下游区域是一个洪涝灾害多发的地区，特大洪水主要受本地1～7 d暴雨径流、上游暴雨洪水和长江洪潮顶托等影响。

设计暴雨历时应不小于流域汇流时间，根据滁河中下游流域地形地貌特性和水文水力分析，取1 d、3 d、7 d为滁河中下游设计暴雨计算的控制时段。以汊河集闸以下滁河中下游流域，1959—2010年的年最大1 d、3 d、7 d暴雨量与南京下关站相应时段的最高潮位资料为例，用Copula函数构建联合分布模型，分析流域暴雨和长江潮位的联合分布概率。

表1 Copula函数参数θ和τ的关系

2 联合分布函数

2.1 Copula函数

Copula函数是将多个随机变量的联合分布函数用他们各自的边际分布表示出来的函数，其边际分布可以采用任何形式。由于Archimedean Copula函数只含有一个参数θ，求解简便适应性强，被广泛应用于水文领域[14-15]，水文中常用的二维Archimedean Copula函数有Clayton Copula函数、Frank Copula函数和GH Copula函数[16-18]，Copula函数参数θ和Kendall秩相关系数的关系表达式见表1。设计暴雨降雨量Rp遭遇潮位区间(Z1,Z2)的概率作为设计暴雨和潮位遭遇的组合概率，计算公式为

P(R≥RP,Z1≤Z≤Z2)=F(Z2)-F(RP,Z2)-F(Z1)+F(RP,Z1)

(1)

式中：R——降雨量；Z——潮位；F(Z1)——潮位Z1的边际分布函数值；F(Z2)——潮位Z2的边际分布函数值；F(RP,Z1)——设计暴雨降雨量Rp与潮位Z1的联合分布概率；F(RP,Z2)——设计暴雨降雨量Rp与潮位Z2的联合分布概率。

设计潮位Zp遭遇雨量区间(R1,R2)的概率作为设计潮位和雨量遭遇的组合概率，计算公式为

P(Z≥ZP,R1≤R≤R2)=F(R2)-F(ZP,R2)-F(R1)+F(ZP,R1)

(2)

式中：F(R1)——雨量R1的边际分布函数值；F(R2)——雨量R2的边际分布函数值；F(ZP,R1)——设计潮位Zp与雨量R1的联合分布概率；F(ZP,R2)——设计潮位Zp与雨量R2的联合分布概率。

2.2 参数估计及拟合度检验

Copula模型选择主要包括离差平方和最小准则(OLS)法、BIC法和 AIC信息准则法[7]，本文选取常用的OLS法，其计算公式为

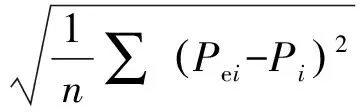
(3)

式中：DOLS——离差平方和；Pei——联合经验概率；Pi——联合理论概率；i——数据系列序号；n——系列长度。

降雨量R和潮位Z的观测样本序列组按降雨量从小到大排列依次为：(R1,Z1)，…，(Rj,Zj)，…，(Ri,Zi)，…，(RN,ZN)，经验联合分布概率计算公式如下：

(4)

式中：Nml——联合观测值样本中满足(Rj≤Ri，Zj≤Zi)的数据对个数；N——总的数据对个数。

3 联合分布函数的构建

3.1 参数估计

边际分布函数采用水利计算中规定的P-Ⅲ型分布函数[19]，矩法计算均值Ex、变差系数Cv和偏差系数Cs的初值，根据综合目估适线法调整不同时段曲线间的关系，分别绘制组合概率P与降雨量R、潮位Z的关系图，如图1所示，参数计算结果如表2所示。表2中R1d为年最大1 d降雨量；R3d为年最大3 d降雨量；R7d为年最大7 d降雨量；Z1d为R1d相应时段的最大潮位；Z3d为R3d相应时段的最大潮位；Z7d为R7d相应时段的最大潮位。

图1 边际分布曲线Fig.1 Marginal distribution curves

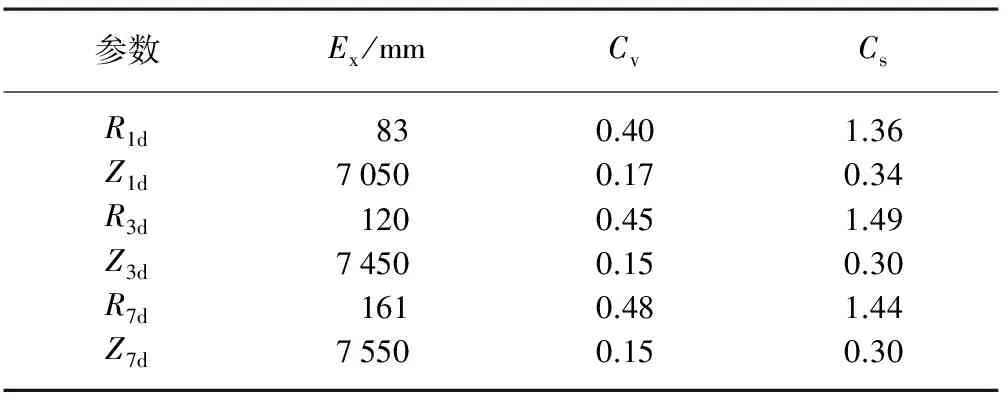
表2 边际分布函数统计参数

表3 Copula函数相关参数

根据实测值求得各个组合的秩相关系数τ，由τ和θ的关系(表1)可以求得参数θ(表3)，R1d与Z1d、R3d与Z3d、R7d与Z7d的秩相关系数分别为0.392、0.348和0.428，3种组合均成正相关，故可以用Archimedean Copula函数进行联合分布计算。采用最小准则法进行精度检验，相关计算参数见表3。

由表3可知，联合分布中，Frank Copula函数的DOLS值最小，表明其拟合效果最佳，故采用Frank Copula函数进行联合分布计算。将R1d与Z1d、R3d与Z3d、R7d与Z7d的经验累积概率和理论累积经验概率绘制在一张图上，如图2所示。

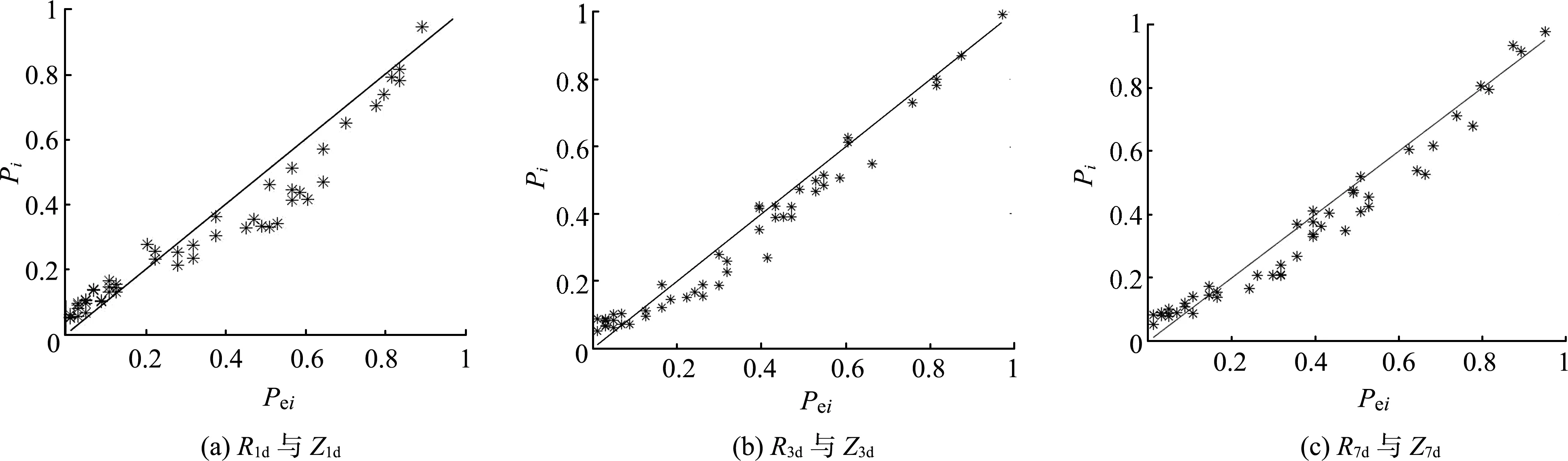
图2 经验累积概率和理论累积概率比较Fig.2 Comparison of empirical and theoretical cumulative probabilities

由图2可以看出，经验累积概率和理论累积概率的点距基本成一条45°的直线，说明所建联合分布模型合理。R1d与Z1d、R3d与Z3d、R7d与Z7d的DOLS值分别为0.108 3、0.086 7和0.088 7，经验概率和理论概率计算值拟合比较好，故可以采用Frank Copula函数进行流域暴雨和潮位的联合分布计算。

3.2 联合分布参数计算

由表2中的边际分布参数可以求得不同量级雨量、潮位所对应的边际分布函数。由表3可以得到Copula函数的统计参数，根据拟合结果选取Frank Copula函数为联合分布函数。由Frank Copula函数关系式及其对应的参数θ，绘制这3种组合的联合分布图(图3)，从图3可以查出任意量级的雨量、潮位组合的联合分布概率。

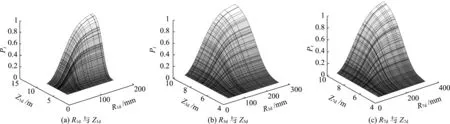
图3 联合分布Fig.3 Joint distribution

4 各量级降雨潮位遭遇组合分析

4.1 设计暴雨与各量级潮位遭遇组合分析

由表2中R1d与Z1d、R3d与Z3d、R7d与Z7d的边际分布参数，计算不同重现期的设计值。分别取重现期为100 a、50 a、20 a、10 a的暴雨作为设计值，由式(1)求得设计暴雨与各量级潮位的联合分布概率，分别绘制1 d、3 d、7 d不同重现期设计暴雨遭遇各量级潮位的组合概率图，如图4所示。

由图4可以看出：(a)同量级潮位，暴雨重现期越小遭遇概率越大；(b)以0.2 m划定不同的潮位区间，同一设计标准的暴雨与各潮位区间的遭遇概率不同；(c)由图4(a)可知，1 d设计暴雨与其相应各量级潮位组合时，100年一遇、50年一遇、20年一遇的设计暴雨遭遇概率最大的潮位区间为(8.2,8.4)，对应于约5年一遇的设计潮位，10年一遇设计暴雨遭遇概率最大的潮位区间为(8.0,8.2)，对应于约4年一遇的设计潮位；(d)由图4(b)可知，3 d设计暴雨与其相应各量级潮位组合时，100年一遇、50年一遇、20年一遇、10年一遇的设计暴雨遭遇概率最大的潮位区间为(8.4,8.6)，对应于约5年一遇的设计潮位；(e)由图4(c)可知，7 d 设计暴雨与其相应各量级潮位组合时，100年一遇设计暴雨遭遇概率最大的潮位区间为(8.8,9.0)，对应于约9 a一遇的设计潮位，50年一遇、20年一遇、10年一遇的设计暴雨遭遇概率最大的潮位区间为(8.6,8.8)，对应于约7年一遇的设计潮位。

4.2 设计潮位与各量级雨量遭遇组合分析

分别取重现期为100 a、50 a、20 a、10 a的潮位作为设计值，由式(2)求得设计潮位与各量级雨量的联合分布概率，分别绘制1 d、3 d、7 d不同重现期设计潮位遭遇各量级雨量的概率图，如图5所示。

由图5可以看出：(a)以15 mm划定不同的雨量区间，同一设计标准的潮位与各雨量区间的遭遇概率不同；(b)由图5(a)可知，1 d设计潮位与其相应各量级雨量组合时，100年一遇、50年一遇、20年一遇的设计潮位遭遇概率最大的雨量区间为(125,135)，对应于约5年一遇的设计降雨，10年一遇设计潮位遭遇概率最大的雨量区间为(105,120)，对应于约3年一遇的设计降雨；(c)由图5(b)可知，3 d设计潮位与其相应各量级雨量组合时，100年一遇设计潮位遭遇概率最大的雨量区间为(180,195)，对应于约5年一遇的设计降雨，50年一遇、20年一遇、10年一遇的设计潮位遭遇概率最大的雨量区间为(165,180)，对应于约3年一遇的设计降雨；(d)由图5(c)可知，7 d设计潮位与其相应各量级雨量组合时，100年一遇设计潮位遭遇概率最大的雨量区间为(255,270)，对应于约7年一遇的设计降雨，50年一遇、20年一遇、10年一遇的设计潮位遭遇概率最大的雨量区间为(240,255)，对应于约6年一遇的设计降雨。

4.3 暴雨潮位组合方法对比

常用线性相关分析法检验流域降雨量和潮位的相关程度，若相关关系较好，则可作为遭遇组合的基础，本次统计筛选出流域降雨量重现期大于5年一遇的暴雨及其对应潮位为研究对象。最大1 d、3 d、7 d流域暴雨重现期与相应长江潮位重现期之间的相关性系数分别为-0.24、0.28、0.91，1 d和3 d暴雨与长江相应潮位之间相关关系不显著，而7 d暴雨与长江相应潮位的相关系数为0.91，相关关系较好，这主要是因为流域及南京上游区域暴雨汇集到长江南京段具有滞时，因此流域7 d暴雨与相应长江潮位可以作为概率组合的基础。绘制7 d流域暴雨与长江潮位重现期相关图，如图6所示。

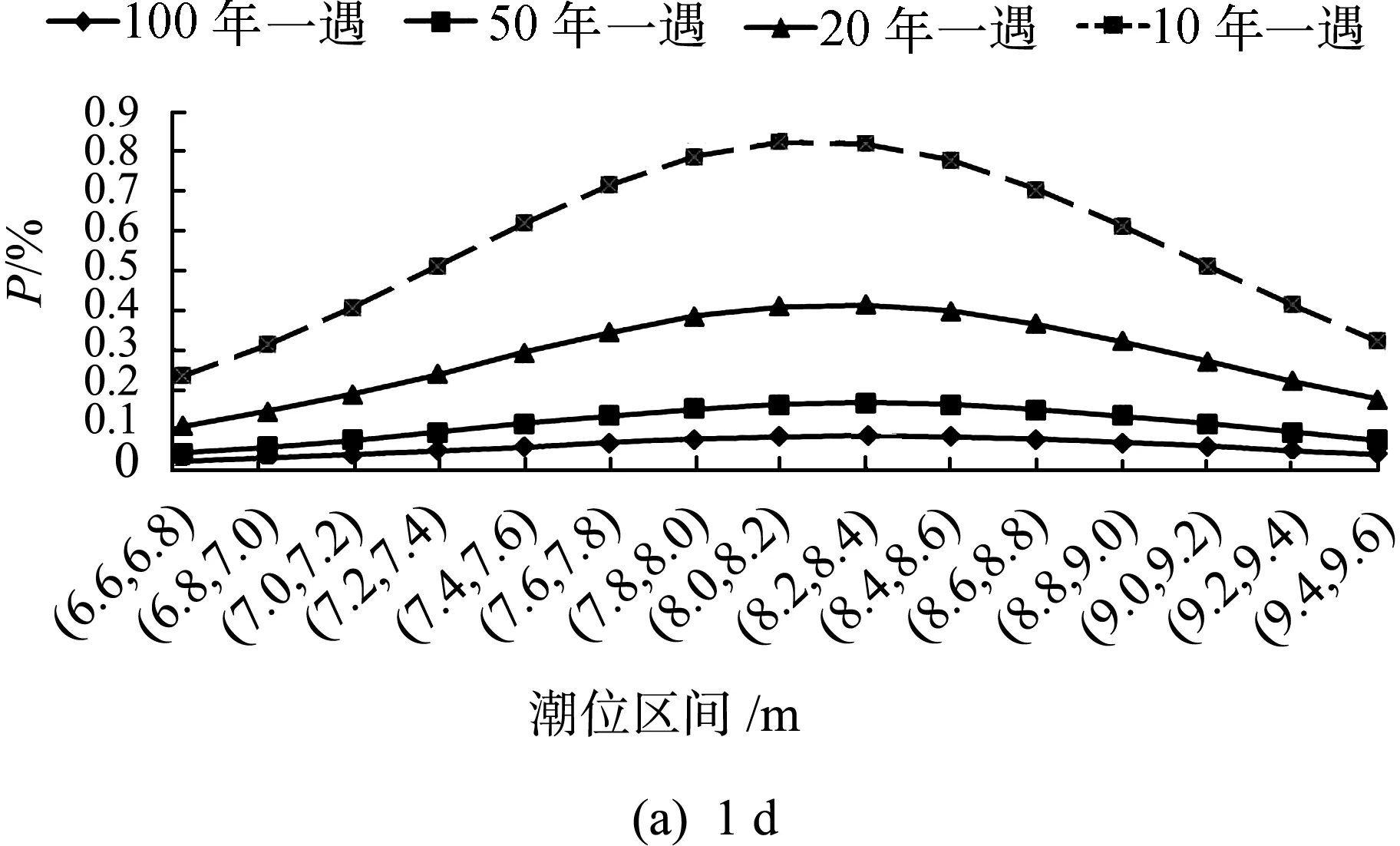
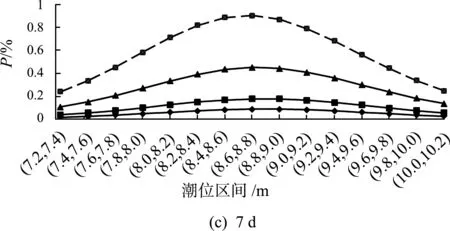
图4 设计暴雨量与各量级潮位组合概率Fig.4 Combined probabilities of design rainstorm and different tide level intervals

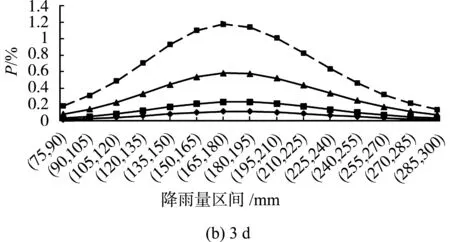
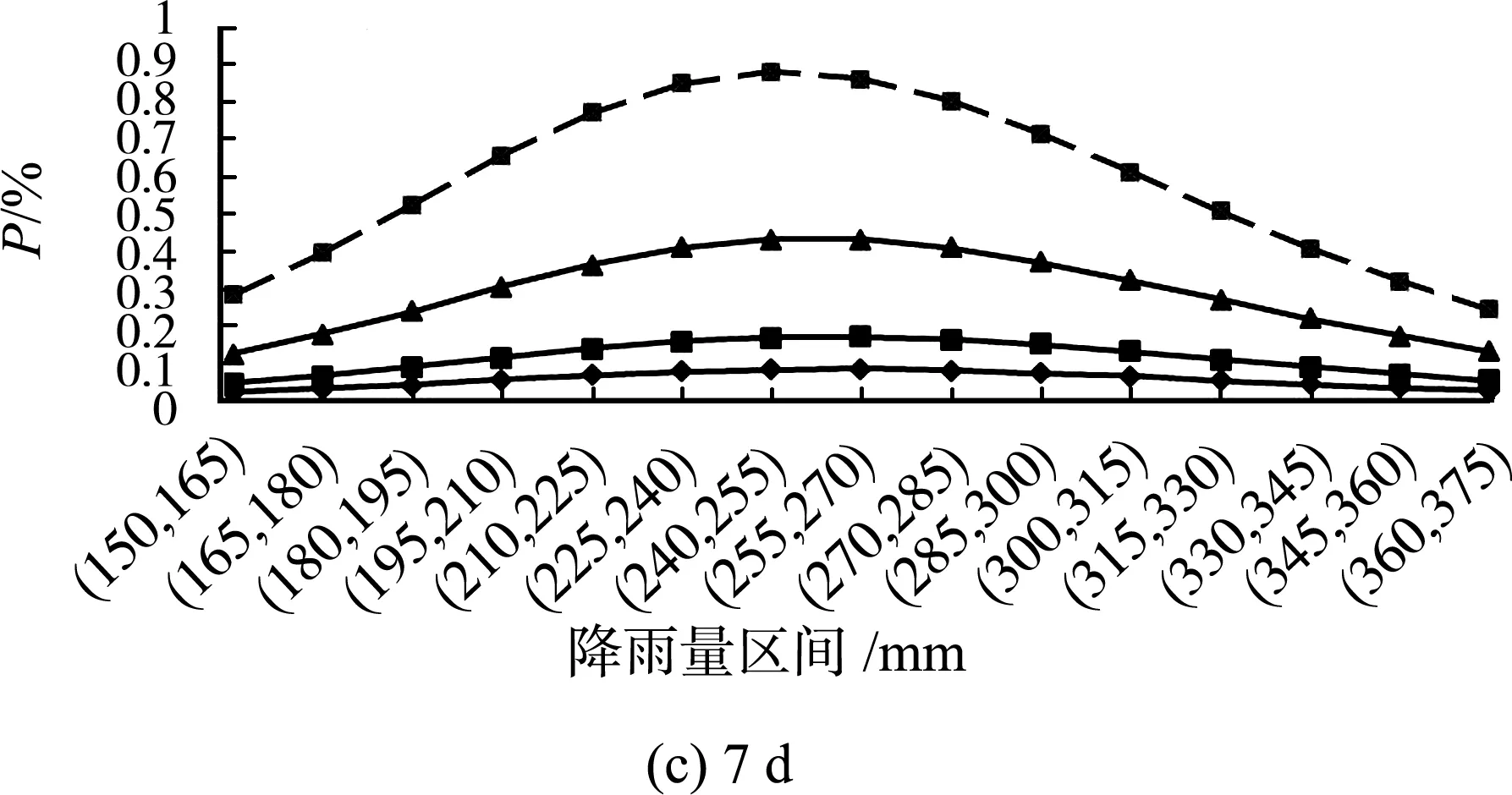
图5 设计潮位与各量级降雨量组合概率Fig.5 Combined probabilities of design tide level and different rainfall intervals

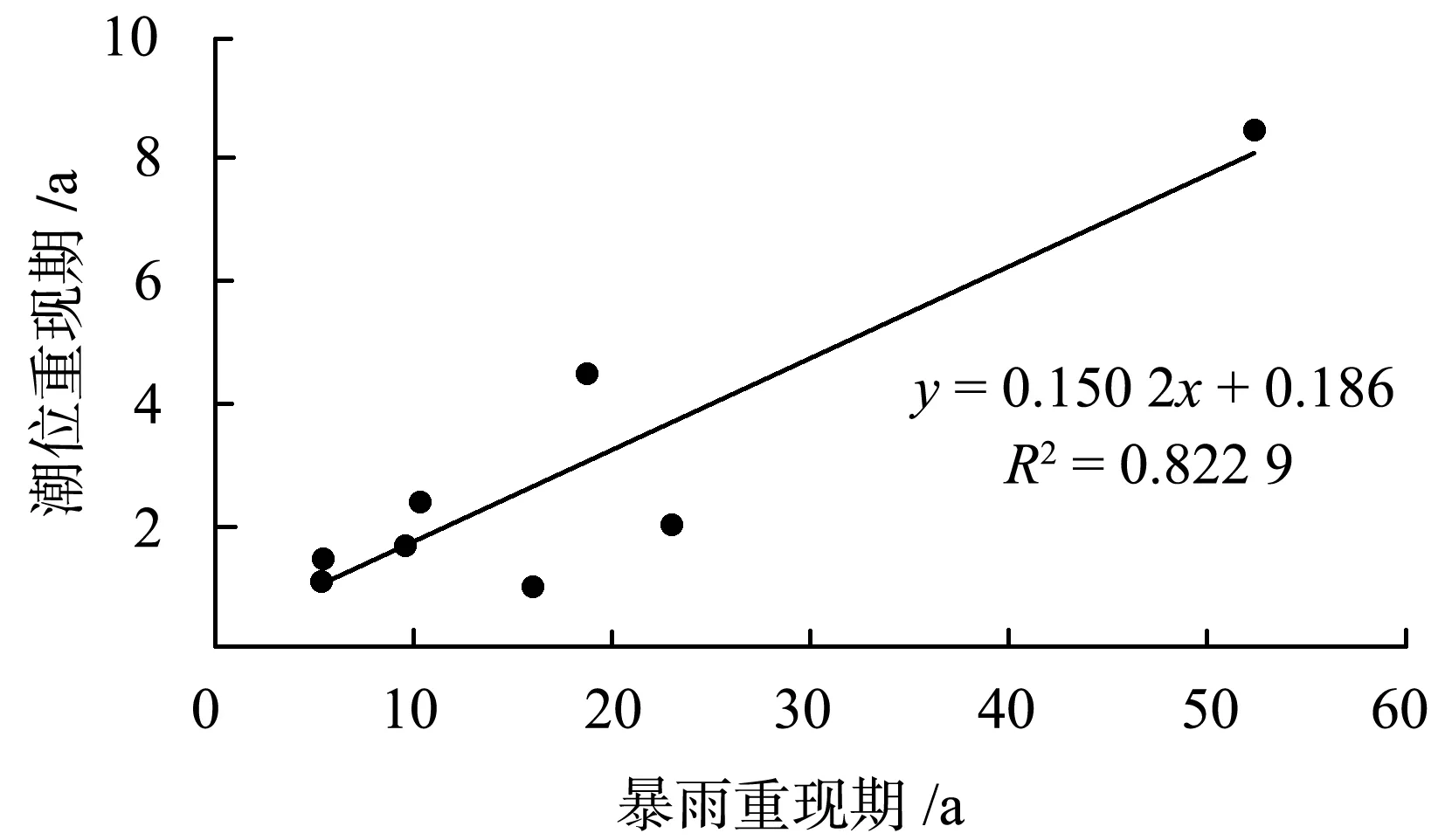
图6 7 d流域暴雨与长江潮位相关性分析Fig.6 Correlation between 7-day rainstorm and tide level of Yangtze River

根据拟合出的流域暴雨与长江潮位组合相关趋势线，分析重现期100年一遇、50年一遇、20年一遇、10年一遇暴雨对应的潮位重现期分别为15 a、8 a、3 a、2 a。

Frank Copula函数计算7 d重现期为100 a、50 a、20 a、10 a设计暴雨遭遇概率最大的潮位重现期为9 a、7 a、7 a、7 a。对比分析2种方法计算结果：设计暴雨重现期为100 a，用Frank Copula函数计算的最大概率遭遇潮位重现期为9 a，比用线性相关分析法计算的15 a小，Frank Copula函数能得到各个组合概率的大小，100年一遇设计暴雨遭遇15年一遇潮位的概率也很大；50年一遇的设计暴雨遭遇潮位重现期，两种方法计算结果一致；20年一遇、10年一遇设计暴雨遭遇潮位重现期均小于10 a。当暴雨潮位的相关性不显著时，相关性分析法的使用受到限制，采用Frank Copula函数可以得到各个组合的遭遇概率，可为感潮河段防洪规划提供科学依据。

5 结 论

a.基于Archimedean Copula函数构建R1d与Z1d、R3d与Z3d、R7d与Z7d的联合分布函数，经过拟合检验，可以采用拟合度最好的Frank Copula函数进行分析计算。

b.基于Frank Copula函数，对1 d、3 d、7 d设计暴雨与各量级潮位组合分析，得到不同设计标准暴雨最大概率遭遇的潮位区间，对1 d、3 d、7 d设计潮位与各量级雨量遭遇组合分析，得到不同设计标准潮位最大概率遭遇的雨量区间。分析结果与南京市城市防洪规划中结论相近，表明方法合理可行，可为其他地区暴雨潮位组合计算提供参考。

[1] 符锐,罗龙洪,刘俊，等. SWMM模型在城市排水防涝系统能力评估中的应用[J]. 中国农村水利水电,2015,389(3):103-105,109.(FU Rui, LUO Longhong, LIU Jun, et al. The application of the drains system capability assessment based on SWMM[J]. China Rural Water and Hydropower,2015, 389(3):103-105,109.(in Chinese))

[2] 芮孝芳,陈浩云. 感潮河段设计洪水位的推求[J]. 水利水电技术,1995(11):39-42. (RUI Xiaofang, CHEN Haoyun. The calculation of design flood level in tidal river[J]. Water Resources and Hydropower Engineering, 1995 (11):39-42. (in Chinese))

[3] AGHAKOUCHAK A, CIACH G, HABIB E. Estimation of tail dependence coefcient in rainfall accumulationelds[J]. Advances in Water Resources, 2010, 33(9): 1142-1149.

[4] GRIMALDI S, SERINALDI F. Asymmetric Copula in multi-variate flood frequency analysis[J]. Advances in Water Resources, 2006, 29(8): 1155-1167.

[5] ZHANG L, SINGH V P. Bivariate flood frequency analysis using the copula method[J]. Journal of Hydrologic Engineering, 2006, 11(2): 150-164.

[6] 郭生练,闫宝伟,肖义，等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文,2008,165(3):1-7. (GUO Shenglian, YAN Baowei, XIAO Yi, et al. Multivariate hydrological analysis and estimation[J].Journal of China Hydrology, 2008, 165(3):1-7. (in Chinese))

[7] 宋松柏, 蔡焕杰, 金菊良，等. Copula函数及其在水文中的应用[M]. 北京:科学出版社, 2012:87-89.

[8] 张翔,冉启香,夏军，等. 基于Copula函数的水量水质联合分布函数[J]. 水利学报,2011,415(4):483-489. (ZHANG Xiang，RAN Qixiang, XIA Jun, et al. Jointed distribution function of water quality and water quantity based on Copula[J]. Journal of Hydraulic Engineering, 2011, 415(4):483-489.((in Chinese))

[9] 侯芸芸,宋松柏,赵丽娜，等. 基于Copula函数的3变量洪水频率研究[J]. 西北农林科技大学学报(自然科学版), 2010,233(2):219-228. (HOU Yunyun, SONG Songbai, ZHAO Lina, et al. Research of trivariate flood frequency based on Copula function[J]. Journal of Northwest A&F University (Nature Sciences), 2010, 233(2): 219-228. (in Chinese))

[10] 张娜,郭生练,闫宝伟，等. Copula函数在分期设计洪水中的应用研究[J]. 水文,2008,167(5):28-32. (ZHANG Na, GOU Shenglian, YAN Baowei, et al. Seasonal design flood based on Copula function[J]. Journal of China Hydrology, 2008, 167(5):28-32. (in Chinese))

[11] 刘曾美,陈子燊. 区间暴雨和外江洪水位遭遇组合的风险[J]. 水科学进展,2009, 92(5):619-625. (LIU Zengmei, CHEN Zisheng. Risk study of the bivariate encounter of interzone rainstorm and flood level of the outer river[J]. Advances in Water Science, 2009, 92(5): 619-625. (in Chinese))

[12] 武传号,黄国如,吴思远. 基于Copula函数的广州市短历时暴雨与潮位组合风险分析[J]. 水力发电学报,2014,145(2):33-40. (WU Chuanhao, HUANG Guoru, WU Siyuan. Risk analysis of combinations of short duration rainstorm and tidal level in Guangzhou based on Copula function[J]. Journal of Hydroelectric Engineering, 2014, 145(2):33-40. (in Chinese))

[13] 郭财秀,李国芳,郑玲玉，等. 长江感潮河段洪潮遭遇组合概率分析[J]. 水电能源科学,2015,184(12):51-54. (GUO Xiucai, LI Guofang, ZHEN Lingyu, et al. Risk probability study on Encounter of flood and tide in tidal reach of the Yangtze River [J]. Water Resources and Power,2015, 184(12):51-54. (in Chinese))

[14] 陆桂华,张亚洲,肖恒，等. 气候变化背景下蚌埠市暴雨与淮河上游洪水遭遇概率分析[J]. 气候变化研究进展,2015,59(1):31-37. (LU Guihua, ZHANG Yazhou, Xiao Heng, et al. Coincidence probability of urban rainstorm in Bengbu and flood in the upper reaches of Huaihe River under climate change [J]. Advance in Climate Change Research, 2015, 59(1):31-37. (in Chinese))

[15] 冯平,李新. 基于Copula函数的非一致性洪水峰量联合分析[J]. 水利学报,2013,445(10):1137-1147. (FENG Ping, LI Xin. Bivariate frequency analysis of non-stationary flood time series based on Copula methods[J]. Journal of Hydraulic Engineering, 2013, 445(10):1137-1147. (in Chinese))

[16] 张冬冬,鲁帆,严登华，等. 基于Archimedean Copula函数的洪水多要素联合概率分布研究[J]. 中国农村水利水电,2015,387(1):68-74，79. (ZHANG Dongdong, LU Fan, YAN Denghua, et al. Research on multi-dimendional joint distribution of flood characteristics based on Archmedean Copula [J]. China Rural Water and Hydropower, 2015, 387(1):68-74+79. (in Chinese))

[17] 郭爱军,黄强,畅建霞，等. 基于Copula函数的泾河流域水沙关系演变特征分析[J]. 自然资源学报,2015,30(4):673-683. (GUO Aijun, HUANG Qiang, CHANG Jiangxia, et al. Variation of relationship between runoff and sediment based on Copula Function in the Jinghe River Basin [J]. Journal of Natural Resources, 2015, 30(4):673-683. (in Chinese))

[18] 闫宝伟,郭生练,郭靖，等. 基于Copula函数的设计洪水地区组成研究[J]. 水力发电学报,2010,125(6):60-65. (YAN Baowei, GUO Shenglian, GUO Jing, et al. Regional design flood composition based on Copula function [J]. Journal of Hydroelectric Engineering, 2010, 125(6):60-65. (in Chinese))

[19] 水利部长江水利委员会水文局.SL278—2002 水利水电工程水文计算规范[S].北京:水利水电出版社,2002.

Combined analysis of rainstorm and tide level based on Copula function

WAN Yongjing1, DIAO Xiumei2, LIU Jun1, ZHOU Hong1, LUAN Mu1, LI Daiyuan3

(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China;2.WaterManagementOfficeofJiangyin,Jiangyin214400,China;3.HydrologyandWaterResourcesDepartment,NanjingHydraulicResearchInstitute,Nanjing210029,China)

Based on the rainstorm data from the middle and lower reaches of the Chuhe River in the period from 1959 to 2010 and the tide level data at Xiaguan Station in Nanjing City, a joint distribution function of the annual maximum 1-day, 3-day, and 7-day rainstorms and the corresponding tide levels of the Yangtze River with different return periods was built based on the Copula function. The encounter probabilities of the design rainstorm and different tide level intervals and the encounter probabilities of the design tide level and different rainstorm intervals were calculated. The results are similar to conclusions in the Nanjing Urban Flood Control Planning, indicating that the calculation method is reasonable and feasible and can provide a reference for combined calculation of rainstorm and tide level.

Copula function; interval storm; tide level of Yangtze River; frequency combination; middle and lower reaches of Chuhe River

10.3876/j.issn.1000-1980.2017.03.004

2016-07-01

中国工程院重大咨询研究项目(2015-ZD-07)；国家自然科学基金(41471015)

万永静(1993—)，女，重庆人，硕士研究生，主要从事城市防洪与排水研究。E-mail：1043347075@qq.com

刘俊，教授。E-mail：ljhohai@163.com

TV122+3

A

1000-1980(2017)03-0211-07