特高压输电线路的大截面导线微风振动特性

张建国，刘建军，李成钢，张 研

(1.国网江苏省电力公司电力科学研究院，江苏 南京 211103；2.河海大学力学与材料学院，江苏 南京 210098)

特高压输电线路的大截面导线微风振动特性

张建国1，刘建军1，李成钢1，张 研2

(1.国网江苏省电力公司电力科学研究院，江苏 南京 211103；2.河海大学力学与材料学院，江苏 南京 210098)

为了掌握用于特高压输电的大截面导线JL1X1/G2A-1520/125-481的微风振动特性，对该型导线建立微风振动控制方程，编程计算了8～80 Hz频段中16个等间距频率点处导线的双振幅值、允许振幅、单位功耗等风振特性，并利用波腹处的最大振幅确定了导线悬挂点在各频率点的动弯应变与动弯应力。研究发现：在自阻尼振动情况下，该型号导线双振幅值随频率增加先增加后降低，在20 Hz附近达到最大值，当振动频率为20～40 Hz时，导线的振动幅值超过其允许幅值；导线的单位功耗随振动频率的增加先增大其后降低，在40 Hz附近达到峰值；在20～40 Hz频段，导线的动弯应变与动弯应力水平偏高，超出了容许值。与普通截面导线的10～20 Hz危险频段相比，大截面导线JL1X1/G2A-1520/125-481的危险频段后移至20～40 Hz，此型号导线的防振消振方案应该重点考虑20～40 Hz频段。

特高压输电线路；大截面导线；微风振动；危险频段；振动特性

电网建设是国家建设的重要方面，是国家经济持续快速发展的重要保障。为了应对我国能源资源和能源消费在空间逆向分布(即经济发达地区能源消耗高而能源资源相对较少，经济欠发达地区能源产出高而消耗量相对较少)的特点，国家电网公司从我国能源战略的高度出发，在“十二五”规划中确定了建设特高压电网的重大战略举措。根据国家电网公司发布的特高压发展规划，我国将逐步建成以特高压为骨干的国家同步电网，实现我国各大区域和主要负荷中心的联接。特高压输电具有远距离、大容量、低损耗、节能减排等方面的优势[1-2]，为了充分发挥其上述优势，在工程建设中会尽可能采用截面较大导线。

根据频率和振幅的不同，输电线的风致振动可分为3种，即高频微风振动、中频次档距振荡和低频舞动。3种振动都会给导线和输电线造成破坏，其中以输电线的高频微风振动发生最为频繁，危害也最大，造成导线和地线疲劳断股、断线，以及金具、杆塔构件的损坏，这些危害对输电线路的安全运行造成极大的威胁[3-6]。由于特高压输电工程导线悬挂点高度以及档距都较大，如采用自重大的大截面导线，导线在风作用下的振动危害将更加突出。目前，国内针对这种新型大截面导线开展的风致振动特性研究较少，亟待开展大截面导线的振动特性研究，为大截面导线的推广应用提供风振防治方面的理论支撑与指导，保障输电线路的安全运行。

国家电网公司新研发了JL1X1/G2A-1520/125-481型导线，其截面高达1 520 mm2，属国内首次，拟大规模推广应用。架空导线存在自然风作用下的振动问题，防振消振不易实现，对于新研发的大截面导线，面临同样的难题。为了解决工程建设中的实际问题，本文研究大截面导线微风振动特性，应用能量平衡原理，建立JL1X1/G2A-1520/125-481型大截面导线振动控制方程，应用动弯应力应变求解方法得到不同频率振动下单导线风振平衡点的单位功耗、振幅和动弯应变，明确该型大截面导线的微风振动特性，为输电线的微风振动控制、抗疲劳设计提供理论依据。

1 导线振动控制方程

当风以稳定风速0.5～10 m/s吹向导线时，在导线背风侧产生上下交替的漩涡，受到上下交变的激励力作用，从而使导线产生振动。这种较高频率(5～150 Hz)、小振幅(小于5 cm)的振动也称为风激振动。

当风速在一定范围内变化时，导线的振动频率和漩涡频率仍会保持不变，这种现象称为同步效应或者锁定效应。由于导线的自振频率均匀密集分布，只要稳定风速吹向导线，谐振便会持续发生。这时，导线的振动沿导线方向呈正弦波形，在振动过程中，同一频率振动波的波节和波腹位置保持不变[7-8]。

1.1 风输入功率

Slethei风输入功率曲线与Diana和Falco风输入功率曲线在工程上得到了广泛应用。由于在低频和振幅较大的情况下，Slethei风输入功率曲线无上限，因此得到的计算结果不符合实际情况。在导线的微风振动中，振动消耗功率随着振幅增加而增加，风输入功率和自阻尼功率总会达到一个平衡点。因此，采用Diana和Falco风输入功率曲线[11-13]。

当稳定的风速垂直吹向刚性圆柱体，圆柱体背风侧气流漩涡脱离时，在圆柱体上作用的升力F随时间成正弦变化，Diana和Falco根据风洞试验提出导线单位长度上的风输入功率Pw为

(1)

式中：y0——双振幅，y0=2A0；A0——单振幅；D——导线外径；f——振动频率；a1、a2、a4——模型参数，一般取a1=0.052 6、a2=1.407 4、a4=2.983 9。

1.2 导线自阻尼功率

导线在振动中自身消耗的功率称为自阻尼功率。从微观上看，导线振动时材料分子间的相对运动产生的热效应是不可逆的[14-16]。振动中导线各股间产生滑动摩擦，导线材料的不均匀性也将产生局部非弹性变形，这些都将导致导线在振动过程中耗散能量，通常将各种能量消耗的因素总称为阻尼。

在导线自阻尼测试中，采用的自阻尼功率Pc的表达式为[1,13]

(2)

式中：β、α——模型系数，由试验测定。

对于JL1X1/G2A-1520/125-481钢芯铝绞线，可以取α=2.259 423+0.013 762f，β=2.374 676+0.076 915 0f，D=48.12 mm。

1.3 导线风振平衡点振动控制方程

根据能量平衡原理，在导线发生谐振时，风输入功率等于导线自阻尼功率，Pw=Pc。应用式(1)和式(2)，则能量平衡方程可以表示为

(3)

式(3)为导线风振平衡点振动控制方程，该方程确定了f与y0之间的隐式关系。给定D，就可以得到f与y0之间的关系曲线。由式(3)可以看出，导线振动的控制方程为超越方程，为了高效、高精度地求解该超越方程，本文应用Fortran语言编制了计算机求解程序。

2 确定动弯应力与应变

由导线在风振平衡点的振动控制方程能够得到导线振动的频率-幅值关系，而利用动弯应变衡量导线的振动强度，以动弯应力分析导线的疲劳性能在工程中应用较为广泛。本节利用导线振幅确定其最大动弯应力和应变值。

当导线微风振动处于稳定状态时，表现为驻波振动，可视为两端固定弦的振动。振动过程中，由于振动波在悬挂点线夹出口处不能继续向前传播而形成波节点，该点因受悬挂装置的约束，不能像档中波节点那样自由转动，通常出现比档中更大的动弯应力和动弯应变。根据这一特点，可以利用波腹处的最大单振幅A0计算导线悬挂点处的动弯应变与应力。当悬挂点为水平夹固时，夹固点对导线弯曲的影响，可视为档距等于半波长的两端夹固情况，在夹固点附近因导线刚度而影响变形。若能求得振动波作用在悬挂点的垂向反力，利用弯曲应力公式便可求得悬挂点的动弯应力与应变。

导线微风振动的驻波谐振函数记为

(4)

式中：x——自振质点到导线悬挂点的距离；t——计算时间；λ——振动波长。在sin2πft=1时刻，导线振动幅值达到最大值。

根据D. Alembert原理，作用在半波长内导线上的振动力可由半波长内各微段导线的质量与其加速度乘积之总和求得。由式(4)可得导线振动的加速度最大值为

a(x)=0(x)=(2πf)2A0sin

(5)

设导线单位长度的质量为m，应用式(5)，则任一微段导线dx上的振动惯性力可以表示为

(6)

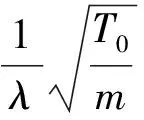
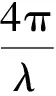
(7)

对于半波长λ/2两端水平夹固导线的情况，应用式(7)可得到悬挂点处动弯应力和应变分别为

(8)

(9)

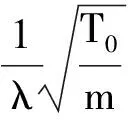
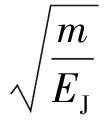
(10)

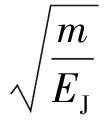
(11)

抗弯刚度EJ和C的取值影响计算的精度，可以根据试验找到适当的修正系数。若已知允许动弯应变εcp(铝股为100×10-6～150×10-6)，由式(11)可以求得允许振幅与频率的临界关系曲线，用于检查实际幅频特性是否超过允许范围。EJ也可取各单股EJ之和∑EJ，这样得到的应力σ和应变ε偏于安全。

3 计算结果与分析

利用Fortran语言编制了振动控制方程的求解程序得到了JL1X1/G2A-1520/125-481(D=48.12 mm)钢芯铝绞线单导线风振平衡点的双振幅y0、单位功耗；利用式(10)和式(11)得到该型导线的允许振幅和动弯应变、应力，如图1～4所示。

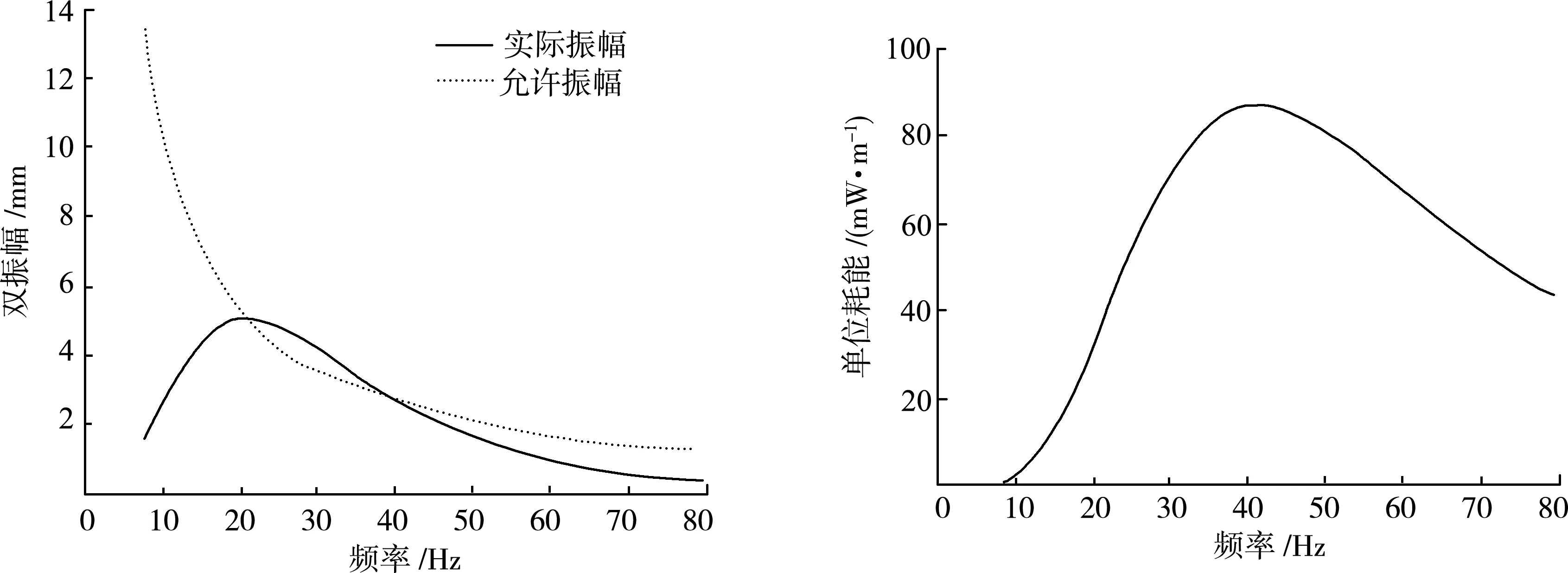
图1 双振幅-频率响应曲线 图2 单位功耗-频率曲线Fig.1 Double amplitude-frequency curve Fig.2 Power dissipation per unit length-frequency curve

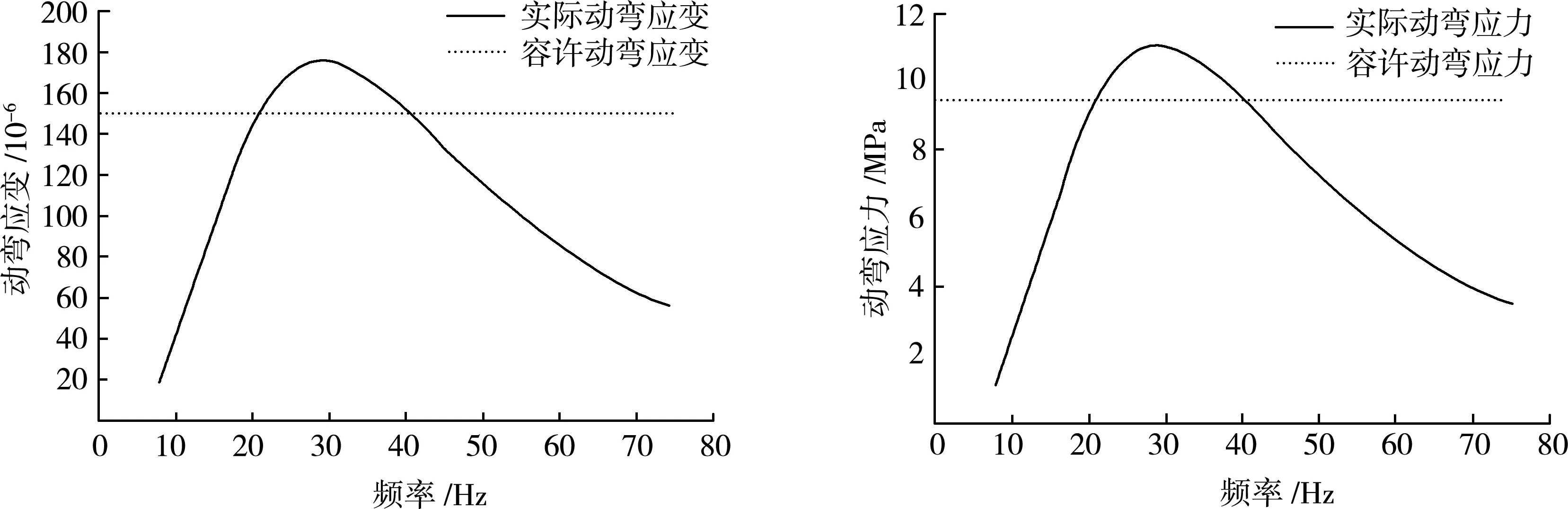
图3 动弯应变-频率曲线 图4 动弯应力-频率曲线Fig.3 Dynamic bending strain-frequency curve Fig.4 Dynamic bending stress-frequency curve

由图1可以看出，导线的双振幅(实线)在低频段较小，随频率的增加而迅速增加，在20 Hz附近达到最大值，约为导线直径的1/10，其后开始逐渐降低，降低速率低于其前期增加的速率，在50 Hz附近幅值降至8 Hz 的振幅。对比其允许幅值曲线，当振动频率低于20 Hz时，导线的振幅低于其允许幅值，当导线振动频率在20～40 Hz之间时，导线的振幅超过其允许幅值，当振动频率低于20 Hz或高于40 Hz时，导线的振幅低于其允许幅值。

由图2可见，导线的单位功耗先随振动频率的增加而提高，在40 Hz附近达到峰值，其后逐渐降低，这表明导线自阻尼功耗能力在20 Hz以下频段较差，在40 Hz附近频段耗能较好，但仍不能将振动幅值控制在允许幅值以下。

根据导线的振幅曲线(图1)，应该在20～40 Hz频段采取针对性的防振措施，降低导线在20～40 Hz频段的振幅，以弥补导线在该频段单位功耗的不足，这也是JL1X1/G2A-1520/125-481与普通截面导线的显著区别。普通截面单导线在低频段(小于20 Hz)幅值一般较高，耗能较低，是抗振设计的重点考虑频段。

导线铝股的动弯应变的允许值一般在100×10-6～150×10-6，这里取上限150×10-6讨论，由图3可见，在20～40 Hz频段，导线的动弯应变明显超出了容许动弯应变，与导线振动的幅频分析结果一致，因而防振方案应该重点考虑导线在20～40 Hz频段的这一振动特性。

动弯应力通常用来衡量导线抗疲劳能力，是架空输电导线抗振设计的重要依据之一，这里的动弯应力由导线容许动弯应变计算得到。由图4可以看出，与导线的容许动弯应变相似，其在20～40 Hz频段的动弯应力超出了容许动弯应力的要求，最高达11.0 MPa，而工程中铝股的疲劳极限通常为10～20 MPa，显然，为了提高导线的抗疲劳能力，必须针对这一频段设计防振方案，防止大截面钢芯铝绞线发生疲劳破坏。

由以上对于大截面导线的振幅、耗能水平、动弯应变应力在频域上分布的具体情况可知，大截面导线的重点抗振防护频段在20～40 Hz这一中频段，与普通截面导线具有显著的差异性，普通截面导线的重点抗振防护频段一般在低频段(小于20 Hz)。

4 结 论

针对JL1X1/G2A-1520/125-481大截面导线，利用能量平衡原理建立了该型导线在风振平衡点的振动控制方程，编制了求解该超越方程的Fortran程序。通过求解振动控制得到了该型大截面导线8～80 Hz频段中16个等间距频率点处导线的双振幅值、允许振幅、单位功耗等风振特性；利用波腹处的最大单振幅确定了导线悬挂点在以上16个频率点的动弯应变与应力。

a.JL1X1/G2A-1520/125-481大截面导线在自阻尼振动情况下，其双振幅值在小于20 Hz频段随频率增加而增加，在20 Hz附近达到峰值，约为导线直径的1/10，其后开始逐渐降低。当导线振动频率在20～40 Hz之间时，导线的振动幅值超过其允许幅值，主要原因为这一频段的导线能耗较低，未能将导线的振动幅值控制在许可范围以下。

b.在20～40 Hz频段，导线的动弯应变、应力明显超出各自的容许值，结合导线振动的幅频分析及单位能耗结果，JL1X1/G2A-1520/125-481型大截面导线防振方案应该重点考虑导线在20～40 Hz频段振动特性，需要采取可靠措施降低导线的振幅、动弯应力应变等指标。

c.普通截面单导线在低频段(小于20 Hz)幅值一般较高，耗能较低，是抗振设计的重点考虑频段，而JL1X1/G2A-1520/125-481型大截面导线在20～40 Hz频段，能耗偏低，其振幅、动弯应力应变偏大，甚至超出了许可值。可见，大截面导线的重点抗振防护频段在20～40 Hz这一频段，导线截面的大幅增加使得导线的危险频段发生漂移，由低频段漂移到了中频段。

[1] 张忠亭. 架空输电线路设计原理[M]. 北京：中国电力出版社, 2010.

[2] FEYZULLAHOGLU E, KARABAY S. Processing damages of material components of aerial conductors and their tribological behaviors under dry friction[J]. Archives of Civil and Mechanical Engineering, 2014, 14(4): 682-690.

[3] 邵天晓. 架空输电线路的电线力学计算[M]. 2版. 北京：中国电力出版社，2003.

[4] 孔德怡，李黎，龙晓鸿, 等.特高压架空输电线微风振动有限元分析[J]. 振动与冲击，2007，26(8) : 64-67.(KONG Deyi,LI Li, LONG Xiaohong,et al. Analysis of aeolian vibration of UHV transmission conductor by finite element method[J].Journal of Vibration And Shock, 2007, 26(8) : 64-67.(in Chinese))

[5] 叶志雄. 输电线微风振动及次档距振荡控制研究[D]. 武汉: 华中科技大学，2009.

[6] AZEVEDO C R F, HENRIQUES A M D, PULINO F A R, et al. Fretting fatigue in overhead conductors: rig design and failure analysis of a Grosbeak aluminium cable steel reinforced conductor[J].Engineering Failure Analysis, 2009, 16(1): 136-151.

[7] 陈元坤. 分裂导线的微风振动与次档距研究[D]. 武汉：华中科技大学, 2011.

[8] KARABAY S, FEYZULLAHOGLU E. Determination of early failure sources and mechanisms for Al 99.7% and Al-Mg-Si alloy bare conductors used in aerial transmission lines[J]. Engineering Failure Analysis, 2014, 38(1): 1-5.

[9] 张子明，周星德，姜冬菊. 结构动力学[M]. 北京：中国电力出版社, 2009.

[10] 王惠民, 赵振兴. 工程流体力学[M]. 南京: 河海大学出版社, 2005.

[11] 徐乃管, 王景朝，宗福琳. 导线自阻尼的测量及实用归算方法[J]. 中国电力,1995, 28(2): 17-20.(XU Naiguan,WANG Jingchao,ZONG Fulin. Conductor self-damping measurement and a practical calculating method[J]. Electric Power, 1995, 28(2): 17-20.(in Chinese))

[12] 徐乃管, 王景朝. 500 kV线路大跨越分裂导线防振试验研究[J]. 电力建设,1994, 15(11): 2-5.(XU Naiguan,WANG Jingchao. Experimental study on anti-vibration behavior of large crossing 500 kV line [J]. Electric Power Construction, 1994, 15(11): 2-5.(in Chinese))

[13] 刘子俊，孙健. 基于遗传算法和神经网络的分时段风速预测方法[J]. 江苏电机工程，2015,34(1): 6-8. (LIU Zijun,SUN Jian. The wind speed prediction based on genetic algorithm and neural network with different periods[J]. Jiangsu Electrical Engineering, 2015,34(1): 6-8.(in Chinese))

[14] AZEVEDO C R F, CESCON T. Failure analysis of aluminum cable steel reinforced (ACSR) conductor of the transmission line crossing the Parana River[J]. Engineering Failure Analysis, 2002, 9(6): 645-664.

[15] FADEL A A, ROSA D, MURÇA L B,et al. Effect of high mean tensile stress on the fretting fatigue life of an Ibis steel reinforced aluminum conductor[J]. International Journal of Fatigue, 2012, 42(8): 24-34.

[16] 刘建军，张廼龙，胡鹏，等. 一起复合横担绝缘子断裂原因的分析与探讨[J].江苏电机工程，2016, 35(6): 88-91. (LIU Jianjun, ZHANG Nailong, HU Peng, et al. Analysis and discussion on the fracture reason of composite cross-arm insulator[J]. Jiangsu Electrical Engineering, 2016, 35(6): 45-49．(in Chinese))

Aeolian vibration property of large cross-sectional conduct for UHV transmission line

ZHANG Jianguo1, LIU Jianjun1, LI Chenggang1, ZHANG Yan2

(1.StateGridJiangsuElectricPowerResearchInstitute,Nanjing211103,China;2.CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing210098,China)

In order to obtain the aeolian vibration property of large cross-sectional conducts JL1X1/G2A-1520/125-481 used for ultra-high voltage (UHV) power transmission, governing equations for aeolian vibration of this type of conduct were constructed. The double amplitude, allowable amplitude, and power dissipation per unit length at 16 equally spaced frequency points in a band of frequencies between 8 Hz and 80 Hz were calculated, and the dynamic bending strain and stress at the suspension point for each frequency point were determined by the maximum amplitude at the antinode. Study shows that, under the self-damping vibration condition, the double amplitude of the conduct increases first and then decreases with the increase of the frequency, with a maximum value at a frequency of near 20 Hz, and the vibration amplitude of the conduct exceeds the allowable value when the vibration frequency ranges from 20 to 40 Hz. The power dissipation per unit length increases first and then decreases with the increase of the frequency, and reaches the peak value at a frequency of 40 Hz. In the band of frequencies between 20 Hz and 40 Hz, the dynamic bending strain and stress of the conduct were greater than their allowable values. Compared with the weakest band of frequencies between10 Hz and 20 Hz of the common cross-sectional conduct, the weakest band of frequencies of large cross-sectional conduct JL1X1/G2A-1520/125-481 is between 20 Hz and 40 Hz, which should be paid more attention in vibration prevention and damping schemes.

UHV transmission line; large cross-sectional conductor; aeolian vibration; weakest band of frequenties; vibration property

10.3876/j.issn.1000-1980.2017.03.013

2016-06-22

国家自然科学基金(51579088)；江苏省自然科学基金(BK20161507)

张建国(1971—), 男, 江苏江阴人,高级工程师, 主要从事电网材料分析与评估研究。E-mail: zjg197108@sina.com

张研,副教授。E-mail:hhu.zhangyan@163.com

TM726.3

A

1000-1980(2017)03-0271-06