轻型飞机副翼操纵系统中改进的RSSR机构研究

谢习华，陈志伟，欧阳星，王小飞，王晓玲

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083)(2.山河智能装备股份有限公司 技术中心，长沙 410100)

轻型飞机副翼操纵系统中改进的RSSR机构研究

谢习华1,2，陈志伟1，欧阳星2，王小飞1，王晓玲1

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083)(2.山河智能装备股份有限公司 技术中心，长沙 410100)

精确控制副翼偏转角度对提高轻型飞机的操纵性能具有重要意义，将改进的空间四连杆机构——RSSR应用于轻型飞机副翼操纵系统的传动末端，采用方向余弦矩阵法建立RSSR机构运动的数学模型，并推导出该机构的位移方程，在ADAMS软件中对该机构进行参数化建模，确定目标函数、约束函数和驱动函数；优化算法选用广义简约梯度算法，对敏感程度较高的设计变量进行优化设计。结果表明：RSSR机构中各点的相对位置对副翼偏转角度影响较大，副翼上下偏转角度的相对误差分别从初始的2.35%与5%降低为0.100 5%与0.103 3%，采用RSSR机构可有效提高对飞机副翼偏转角度的控制精度。研究成果最终应用于某五座复合材料轻型飞机样机中。

轻型飞机；副翼操纵系统；RSSR；ADAMS；优化设计

0 引 言

由于轻型飞机轻便、安全、对起降场地要求低、易操作、物美价廉等优点，被广泛用于私人飞行、公务飞行、商业运输等用途，据统计，全世界目前共有40万架轻型飞机[1]。轻型飞机主机械操纵系统由升降舵操纵系统、副翼操纵系统和方向舵操纵系统组成，其中副翼操纵系统的功用是供飞行员操纵副翼以保持飞机的横向平衡或做横向滚转运动[2]。

近20年来，随着计算机技术的发展，在改进的空间四连杆机构——RSSR(Revolute Spherical Spherical Revolute)的研究方面涌现出多种研究方法，例如，矢量法、方向余弦矩阵法、复数法、图解法等[3-6]。张启先[7]采用一种较为通用的方法——方向余弦矩阵法对空间机构进行了研究；该方法首先应用于平面机构的设计分析，而后又被推广到空间机构，结合计算机辅助方法的方向余弦矩阵法更是被广泛应用于空间机构的研究[8-9]。

RSSR机构曾被应用于飞机辅助动力装置(APU)[8]、飞机舵机的四个舵翼[9]等机械结构中，其具有占用空间小、传动效率高等特点，对于空间尺寸有限、传动精度要求高的场合，例如飞机副翼操纵系统等，尤为适用。

本文在副翼操纵系统中采用推拉软轴与空间四连杆机构组合传动的方式，将改进的RSSR机构应用在轻型飞机副翼操纵系统的传动末端，当操纵手柄向左偏转到极限位置时，预期左副翼向上偏转角度为20°，右副翼向下偏转角度为15°；当操纵手柄向右偏转到极限位置时，预期左副翼向下偏转角度为15°，右副翼向上偏转角度为20°。为了达到该设计目标，运用ADAMS软件的优化设计模块对初始机构参数进行优化设计，得到满足设计要求的各运动参数，以期为未来进行轻型飞机操纵系统关键部件的设计提供参考。

1 RSSR机构的运动学建模

1.1 机构自由度计算

针对国内自主研制的首款五座复合材料轻型飞机副翼操纵系统中的RSSR机构进行研究。该五座轻型飞机样机如图1所示。

在CATIA软件中设计的RSSR机构的三维模型如图2所示。

RSSR机构简图如图3所示。该机构由三连杆1、2、3和机架4组成，机架4上的转轴O1与O4之间有一扭角α14，该机构实现了不在同一平面内的杆件转动的运动变换。

对空间机构的自由度计算普遍采用Grübler-Kutzbach(G-K)公式[10-11]：

(1)

式中：n为活动构件数；p为运动副的总数；fj为第j个运动副的自由度数。

由于只需考虑连杆1和连杆3之间的运动关系，连杆2绕自身轴线的转动对机构运动没有影响，在计算自由度时应去除连杆2绕自身轴线转动的局部自由度。则RSSR机构的自由度为

RSSR机构的自由度是1，则机构在运动过程中只需要一个驱动即可实现确定的运动。

1.2 机构数学模型建立

在输入杆3、输出杆1和机架4上分别固结坐标系O3x3y3z3、O1x1y1z1和O4x4y4z4[12]，其他参数定义如图3所示。直接采用方向余弦矩阵法对RSSR机构的位移进行求解较为困难，为了便于研究，采用拆分方法将图3中的RSSR机构在连杆2处进行拆分。该机构分解为两个不含球面副的机构系统，对拆分后的机构利用方向余弦矩阵进行坐标变换，可得到图3中A、B两点的绝对坐标值。由于连杆2的杆长d2为一定值，联立A、B两点绝对坐标值即可建立该机构的求解方程。具体求解过程如下：

(1) 确定A、B两点在坐标系O4x4y4z4中的坐标。从图3可以看出A点在O1x1y1z1中的坐标为

(2)

由方向余弦矩阵坐标变换公式可得A点在O4x4y4z4中的坐标为

(3)

同理可得B点在O4x4y4z4中的坐标为

(4)

(2)A、B两点的杆长约束方程为

(5)

(3) 将式(3)～式(4)代入式(5)，化简得到输出角θ1的三角方程式：

Xcosθ1+Ysinθ1+Z=0

(6)

其中，

(7)

(8)

(9)

求解式(6)可得θ1的表达式为

(10)

式(10)表明给定输入杆一个位置，则输出杆有两个可能位置，具体取值需要按照机构装配方案和运动连续性来确定。

2 RSSR机构在轻型飞机副翼操纵系统上的应用

轻型飞机的副翼操纵系统大多是借助推拉钢索或连杆直接操纵舵面的，驾驶杆通过机械链系与操纵面相连，操纵面的偏角和气动载荷、操纵位移成比例，飞机的气动特性直接转换为操纵特性[13]。飞行员通过驾驶杆的杆力和杆位移可以直接感受舵面气动力的变化和飞机的运动，驾驶杆的杆力和杆位移与舵面偏转一一对应，而在其操纵系统传动末端的RSSR机构对飞机的飞行品质具有至关重要的影响。

副翼操纵系统的功能是操纵副翼偏转以实现飞机的横向控制。通常副翼的运动为差动[14]，部分民用飞机通常设计成副翼上偏的角度远大于其下偏的角度，其原因是副翼上偏时需要较大的偏转角度才能满足气动效率。

某轻型飞机的操纵系统采用推拉软轴与空间四连杆机构组合操纵舵面，主要由操纵手柄、传动连杆、推拉软轴、双摇臂、RSSR机构和副翼等组成。RSSR机构的输入杆即为双摇臂中的从动摇臂，通过操纵手柄向左右偏转到极限位置时，左右副翼相应的偏角应能够达到设计目标，偏转角度精度要求为±0.1°。传动特性分析的重点在于输出角度能否满足设计要求，因此，本文主要对连杆机构的角位移进行研究，运动分析中的速度和加速度则不作分析。根据空间结构要求，对图3中的结构参数的初值拟定为：

3 RSSR机构的参数优化设计

RSSR机构中的各杆长度是影响输出轴角度的主要参数，在图3中b14的长度是固定不变的，其余各杆长度由O1、A、B、O3四点在O4x4y4z4中的坐标来确定，因此设定这四点在O4x4y4z4中的坐标值作为设计变量并对其进行参数化。在ADAMS软件中建立仿真模型，对设计变量的敏感度进行分析，并对敏感度较高的设计变量进行优化，最终得到符合设计目标的最优机构参数。

ADAMS可提供OPTDES-GRG(广义简约梯度算法)和OPTDES-SQP(序列二次规划算法)两种算法[15]。通过分析和比较，本文采用数学规划法中的广义简约梯度法作为优化算法，该方法是目前求解非线性约束优化问题最有效的手段之一。

3.1 参数化仿真模型建立

根据图3和初始杆长及参数，在ADAMS中建立RSSR机构的初始位置三维模型，对构件连接点在O4x4y4z4中的坐标值进行参数化，并将参数化点分别命名为Pt_O3、Pt_B、Pt_A和Pt_O1，不计重力，添加运动副和驱动后的模型如图4所示。

为了方便程序参数化，设定测量输入杆3输入角度名称为Inp_Ang，测量输出杆1输出角度名称为Outp_Ang，输入杆中与Pt_O3相关联的MARKER点名称为MARKER_O3，输出杆中与Pt_O1相关联的MARKER点名称为MARKER_O1。优化输出杆1输出角度的目标函数为

Minimum of：ABS(MAX(Outp_Ang)-15)+ABS(MIN(Outp_Ang)+20)

即副翼偏转角度满足上偏20°、下偏15°的要求。

定义约束函数为

Minimum of：ABS(DX(MARKER_O3,MARKER_O1)-185.6)

即在优化过程中，求解器在保证b14为185.6 mm时，目标函数达到最优。

定义驱动函数为

STEP(time,0,0d,5,25d)+STEP(time,5.1, 0d,15,-50d)+STEP(time,15.1,0d,20,25d)

即驱动输入杆运动一个周期。

为了研究各设计点对目标函数的影响程度，在ADAMS的Design Evaluation模块中选择设计研究选项Design Study，对设计点初始值进行设计，可得设计点初始值对目标函数的敏感程度，如表1所示。

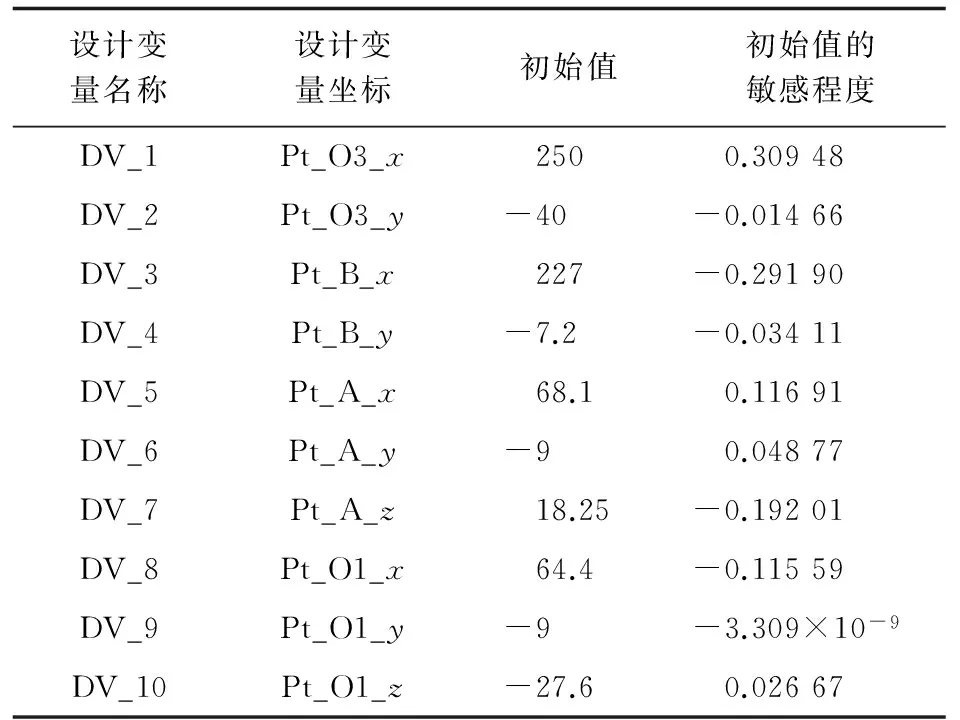
表1 设计点初始值对目标函数的敏感程度

从表1可以看出：O3、B、A、O1四点的初始位置的x坐标和A点的初始位置的z坐标(变量DV_1、DV_3、DV_5、DV_8和DV_7的初始值)对目标函数的敏感度最大，即对目标函数的影响最大，通过对上述五个参数进行优化可明显改善副翼的偏转角度。

3.2 优化设计

在ADAMS的Design Evaluation模块中设置相应的目标函数和约束函数，优化算法选择OPTDES-GRG，差分方式选择Centered(中心差分法)。优化前后的曲线如图5～图7所示，其中Inp_Ang的方向与图3中的方向相反。

从图5～图7可以看出：优化后副翼向上偏转角度为19.979 9°，向下偏转角度为15.015 5°，摆角误差分别为-0.020 1°和0.015 5°，在精度要求的±0.1°之内，相对误差分别为0.100 5%和0.103 3%。

敏感度较大的设计变量的优化值如表2所示，优化后各杆长度如表3所示。优化结果表明，通过优化初始位置和各杆长度后，可以得到高精度的上下差动角。

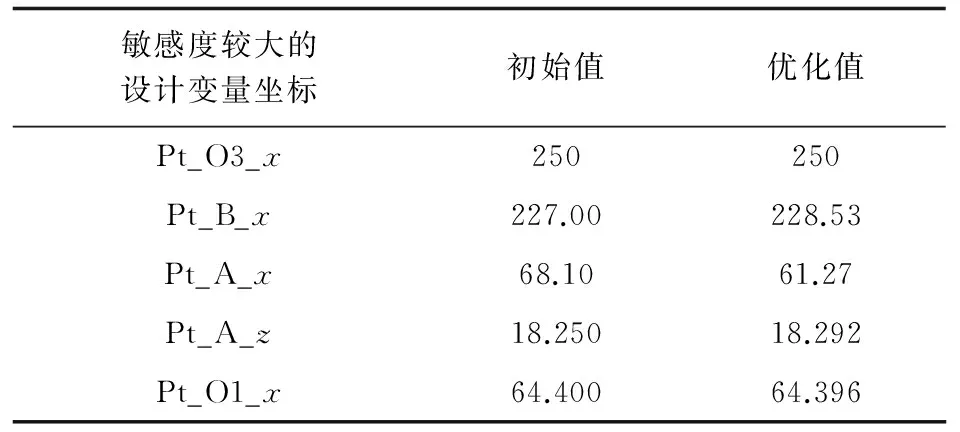
表2 敏感度较大的设计变量优化值

表3 优化后各杆长度参数

将优化后的RSSR机构在CATIA中进行三维建模，经验证，机构不存在干涉，很好地满足了设计要求。

4 结 论

(1) 副翼操纵系统传动末端的RSSR机构中各点的初始位置对副翼偏转角度影响显著，优化结果表明，RSSR机构中连杆的两端点位置对输出杆的输出角度影响最大；通过优化对输出杆输出角度有较高敏感度的设计变量，能够使副翼上下偏转角度达到较高的精度。

(2) 优化后的RSSR机构已成功应用于某五座轻型飞机样机中，本文的研究结果对未来指导轻型飞机操纵系统关键部件设计具有重要意义。

[1] 黄国龙, 张利国. 轻型飞机纵向操纵系统参数化设计与仿真研究[J]. 中国高新技术企业, 2014(33): 33-35. Huang Guolong, Zhang Liguo. Parametric design and simulation research of light aircraft longitudinal control system[J]. China High-Tech Enterprises, 2014(33): 33-35.(in Chinese)

[2] 黄汉军. 飞机机械操纵系统的传动性能计算分析与优化设计研究[D]. 西安: 西北工业大学, 2005. Huang Hanjun. Analysis and optimal design of transmission performance of aircraft mechanical control system[D]. Xi’an: Northwestern Polytechnical University, 2005.(in Chinese)

[3] 刘静. 空间四杆机构的解析综合及程序设计[J]. 江西有色金属, 1998(4): 41-44. Liu Jing. Analysis synthesis and program design of spatial four bar mechanism[J]. Jiangxi Nonferrous Metals, 1998(4): 41-44.(in Chinese)

[5] 苗鸿宾, 乔峰丽. 空间RSSR机构运动分析的研究[J]. 机械设计与制造, 2008(2): 11-13. Miao Hongbin, Qiao Fengli. Kinematics characteristics analysis research of spatial RSSR mechanisms[J]. Machinery Design & Manufacture, 2008(2): 11-13.(in Chinese)

[6] Ge Ming, Han Xuefeng, Jia Hongguang. The parameter optimization of missile actuator based on spatial RSSR linkage mechanism[C]//2011 International Conference on Electric Information and Control Engineering, 2011.

[7] 张启先. 空间机构的分析与综合[M]. 北京:机械工业出版社, 1984: 286-361. Zhang Qixian. Analysis and synthesis of spatial mechanism[M]. Beijing: China Machine Press, 1984: 286-361.(in Chinese)

[8] 刘建伟. 飞机APU进排气门机构设计及性能分析[D]. 南京: 南京航空航天大学, 2012. Liu Jianwei. Design and performance analysis of aircraft APU intake and exhaust valve mechanism[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2012.(in Chinese)

[9] 周啸, 宋梅利, 王晓鸣, 等. RSSR空间机构的运动分析和优化设计[J]. 机床与液压, 2015, 43(9): 1-4. Zhou Xiao, Song Meili, Wang Xiaoming, et al. Motion analysis and optimization design of RSSR spatial mechanism[J]. Machine Tool & Hydraulics, 2015, 43(9): 1-4.(in Chinese)

[10] 韩建友, 杨通, 于靖军. 高等机构学[M]. 2版. 北京: 机械工业出版社, 2015: 26-33. Han Jianyou, Yang Tong, Yu Jingjun. Advanced mechanisms[M]. 2nd ed. Beijing: China Machine Press, 2015: 26-33.(in Chinese)

[11] 卢本兴. 一种空间四杆机构的运动学分析及仿真[J]. 北华航天工业学院学报, 2013, 23(4): 1-3. Lu Benxing. Kinematics and simulation for a spatial four-bar likage[J]. Journal of North China Institute of Aerospace Engineering, 2013, 23(4): 1-3.(in Chinese)

[12] 何勇, 顾玉莲, 吴兴培. 空间RSSR机构向球面4R机构的转化[J]. 机械工程学报, 2009, 45(10): 30-35. He Yong, Gu Yulian, Wu Xingpei. Transformation from spatial RSSR mechanism to spherical 4R mechanism[J]. Journal of Mechanical Engineering, 2009, 45(10): 30-35.(in Chinese)

[13] 沈永奎. 飞机操纵系统建模与仿真研究[D]. 西安: 西北工业大学, 2005. Shen Yongkui. Modeling and simulation of aircraft control system[D]. Xi’an: Northwestern Polytechnical University, 2005.(in Chinese)

[14] 张伟, 李敬. 飞机副翼操纵系统非线性传动特性研究[J]. 计算机仿真, 2015, 32(3): 114-118. Zhang Wei, Li Jing. Research on nonlinear transmission of aileron flight control system[J]. Computer Simulation, 2015, 32(3): 114-118.(in Chinese)

[15] 李增刚. ADAMS入门详解与实例[M]. 北京: 国防工业出版社, 2014: 276-303. Li Zenggang. ADAMS detailed introduction and examples[M]. Beijing: National Defense Industry Press, 2014: 276-303.(in Chinese)

(编辑：马文静)

Research on Improved RSSR Mechanism of Light Aircraft Aileron Control System

Xie Xihua1,2, Chen Zhiwei1, Ouyang Xing2, Wang Xiaofei1, Wang Xiaoling1

(1.Key State Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)(2.Center of Technology, Sunward Intelligent Equipment Co., Ltd., Changsha 410100, China)

In order to make the angles of aircraft aileron deflection can be controlled more accurately, an improved spatial four-bar mechanism-RSSR is applied to the end of the transmission mechanism of the light aircraft aileron control system. The mathematical model of the mechanism is established by the method of direction cosine matrix, and the displacement formula of the mechanism is derived. In order to make an optimization design of RSSR mechanism, the parametric model of the mechanism is established in the software of ADAMS, the objective function, the constraint function and the driving function are determined, the optimal design of the design variables with high sensitivity is carried out by the generalized reduced gradient algorithm. The results show that the aileron deflection angle has great influence by the relative position of each point of the RSSR mechanism, the relative error of the deflection angle of the aileron upward and downward are reduced from the initial 2.35% and 5% to 0.100 5% and 0.103 3% respectively, which demonstrated the optimization design for the mechanism meet the requirements of precision exactly. This research has been used in a prototype of a 5-seat composite material light aircraft finally.

light aircraft; aileron control system; RSSR; ADAMS; optimization design

2017-01-24；

2017-02-25

湖南省科技计划项目(2016wk2032)

谢习华,xxh_zh@csu.edu.cn

1674-8190(2017)02-213-06

V271.9

A

10.16615/j.cnki.1674-8190.2017.02.014

谢习华(1969-)，男，博士，副教授。主要研究方向：特种机器人与飞行器设计。

陈志伟(1993-)，男，硕士研究生。主要研究方向：轻型飞机操纵系统设计。

欧阳星(1986-)，男，博士。主要研究方向：飞机总体设计。

王小飞(1990-)，男，硕士研究生。主要研究方向：轻型飞机操纵系统设计。

王晓玲(1993-)，女，硕士研究生。主要研究方向：精密运动及控制。