筋的截面形状对薄壁结构振动疲劳性能的影响

刘双燕，涂玉倩，苗应刚，李玉龙

(西北工业大学 航空学院，西安 710072)

筋的截面形状对薄壁结构振动疲劳性能的影响

刘双燕，涂玉倩，苗应刚，李玉龙

(西北工业大学 航空学院，西安 710072)

筋条的截面形状对薄壁结构的振动疲劳性能具有重要影响。对L型和T型加筋薄板进行振动试验，研究固支条件下L型筋和T型筋对薄板频率和振动疲劳寿命的影响，并从理论角度分析其原因；利用MSC有限元软件研究在正弦分布载荷下六种不同截面形状(矩形、L型、T型、I型、Z型、∏型)的筋条在给定边界条件(固支、简支)下，对薄板的频率、应力和振动疲劳寿命的影响，并对加筋板的寿命进行预测。结果表明：六种加筋构型中，Z型加筋板的第一阶固有频率最大，加筋板Von Mises应力最大点出现在同样的位置；固支条件下，加筋板的破坏位置在板的左右两侧，Z型加筋板寿命最长；简支条件下，破坏位置出现在板的中央，L型加筋板的寿命最长。

薄壁加筋结构；截面形状；固有频率；Von Mises；振动疲劳寿命

0 引 言

薄壁结构广泛应用于航空、航天、汽车、船舶等领域。由于该类结构刚度、强度、屈曲、振动等力学性能薄弱，在实际应用中一般都采用加筋构型，例如飞机机翼整体壁板、发动机机匣、导弹壳体、航天飞机的外部燃料箱等都属于典型的加筋结构。筋条的形状、尺寸与布局直接影响着结构的重量与性能。

国内外很多学者研究了筋条的布局、尺寸对结构强度的影响。Y.C.Lam等[1]采用变厚度法系统地研究了板结构的加筋布局问题。J.Luo等[2]提出了一种考虑筋条位置与方向的加筋设计方法,并用于静载和特征值问题。L.A.Krog等[3]研究了静载和自由振动下含加强肋板结构的拓扑优化问题。D.Bojczuk等[4]采用加筋板单元研究了平面内载荷和弯曲载荷下Kirchhof板的加筋布局和形状优化。A.Kallassy等[5]和J.Fatemi等[6]以筋条位置为变量、刚度为目标研究了平板结构的加筋布局。

S.H.Crandall等[7]首次提出振动疲劳的概念，并将其定义为结构在振动疲劳下产生的不可逆累积性损伤或破坏。H.Y.Liou等[8]基于随机振动理论提出了一个用于估计结构疲劳寿命的修正模型。王明珠等[9]提出了一种结构随机振动疲劳寿命估算的样本法,通过该样本法能够处理在频域内用谱密度描述的宽带随机振动载荷的情况。张积亭等[10]在飞机典型构件振动疲劳寿命估计中提出，利用随机响应功率谱密度求出的特征频率作为平均频率，在数据处理中是一种较方便的方法。郭建平等[11]针对机载电子设备随机振动问题，采用MSC.FATIGUE软件进行随机振动疲劳分析，计算了疲劳寿命大小及分布；通过对比计算结果与试验结果，证明了利用随机振动疲劳分析方法预测此类产品的疲劳寿命是可行的。陈安等[12]采用了一系列试验方法研究铝锂合金铆接结构疲劳性能。

加筋板和振动疲劳已有很多研究成果，但是将两者结合的研究仍鲜有报道。本文主要内容是将二者结合起来，研究在固支和简支条件下筋条的截面形状对加筋板振动疲劳性能的影响，为航空航天等领域的应用提供理论和试验依据。

1 振动疲劳试验

1.1 试验件设计

为了模拟航空结构中典型的加筋薄壁结构特征，试验件设计为双加筋板，平板厚度为1.6 mm，加筋板平面尺寸及筋条布局如图1所示。筋条的截面形状分别选用L型和T型，如图2所示(筋条长度均为200 mm)。

薄壁结构的平板和筋条分别为2024-T3和LY12CZ铝合金，两种材料的化学成分如表1所示，性能参数如下：弹性模量E分别为72和70 GPa，泊松比ν均为0.3，密度ρ为2 770和2 800 kg/m3，屈服极限σs为275和270 MPa。为了保证试验数据的可靠性，L型和T型试样各取6件，并采用6件不加筋的平板作为参照试样组。

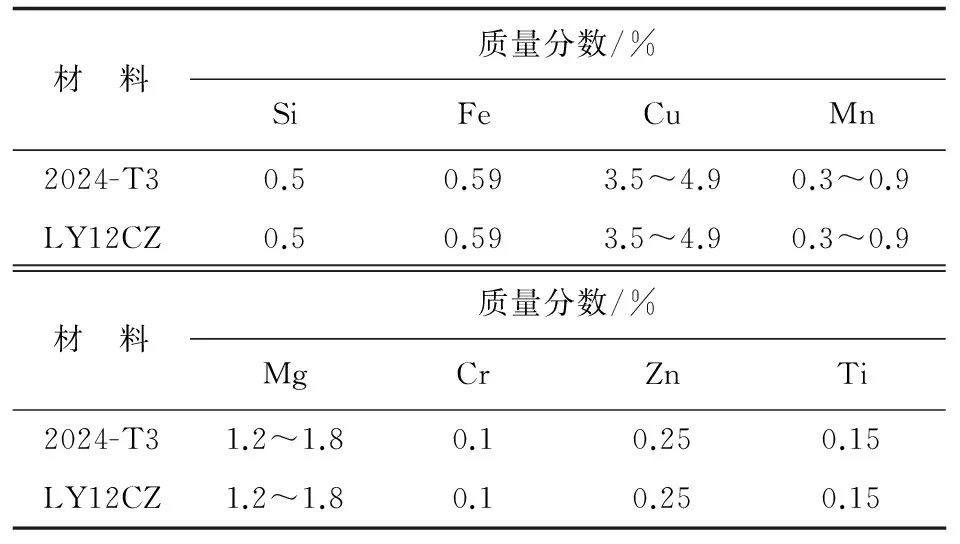
表1 铝合金成分表

试验中设计的夹具由45号钢制成，分为a、b两部分，如图3所示。a部分通过8枚M12螺栓安装固定在振动台台面上，将薄壁结构试样水平放置在夹具a部分的上表面，之后将夹具b部分置于试样上方，用20个M8沉头六角螺栓将夹具a部分、试样和夹具b部分连接，模拟四边固支的边界条件。

1.2 试验方案

试验所使用的设备包括m+p振动控制仪及配套的Vibcontrol控制软件、东菱电动振动台、BE120-3AA应变片(规格为120 Ω)、东华DH3841应变放大器和DEWE-801动态信号采集系统。

薄壁结构的振动疲劳试验原理如图4所示。贴有应变片的试样被夹具以四边固支的方式安装夹持在振动台上如图5所示，应变片位于图中数字标号附近。

振动疲劳激励系统由m+p Vibcontrol振动控制仪和东菱电动振动台组成。振动激励的加载谱等振动参数由振动控制仪传给振动台，从而驱动振动台以产生相应的振动，加速度计将采集到的振动信号反馈给控制仪，控制仪根据控制谱的要求对激励信号进行实时修正以保证振动疲劳加载的持续性。试验过程中试样的固有频率和应变均方根(Root Mean Square，简称RMS)值变化历程由应变片采集到的动态应变信号经动态应变放大器放大后输入DEWE-801动态信号采集系统进行存储和后续处理分析。

试验加载历程如下：首先对各试样施加1 g正弦扫频载荷，得到相应的频率响应曲线和第一阶固有频率；然后，对各试样加载频带范围在其固有频率0.8～1.2倍之间的幅值为10 g2/Hz的随机振动载荷谱，以固有频率降低5%[13]作为试样疲劳破坏的判据，对各试样进行足够长时间的振动，从而得到其振动疲劳寿命。对薄壁结构采用随机激励，而不是正弦或正弦驻留等激励方式，是因为薄壁结构比梁结构复杂，用正弦激励难以保证加载的稳定性，而且随机激励方式更接近薄壁结构服役时的真实载荷环境。

对三种板各进行六次重复试验，将每种板得到的寿命值进行统计分析，得到其寿命在置信度为95%时的上下置信区间和中值疲劳寿命，结果如表2所示。

表2 试样的振动疲劳试验结果

2 振动疲劳试验的模拟验证

2.1 有限元建模

利用有限元分析软件MSC.PATRAN 建立试验件的有限元模型。平板和筋条的尺寸与试验保持一致，平板的四边采用固支的边界条件，使得其有效平面尺寸为220 mm×220 mm，板结构为壳单元，网格细化到5 mm，筋条采用实体单元，筋条与平板之间为绑定连接，T型加筋板的有限元模型如图6所示。

在有限元模拟中，为了得到准确的振动疲劳寿命，需要输入结构的品质数Q[14]，

(1)

式中：f0为固有频率；Δf为半功率带宽，Δf=f2-f1。f0、f1和f2可以从试验所得对应加筋板的频率响应曲线得到。

利用MSC.PATRAN及MSC.NASTRAN，结合品质数模拟得到各板的频率响应关系，再利用MSC.FATIGUE有限元软件对各板施加试验过程中所加载的载荷谱，并进行振动疲劳寿命分析，得到平板、T型和L型加筋板的损伤图，从而得到其振动疲劳寿命。

2.2 模拟验证结果

通过试验和模拟得到平板、T型和L型加筋板的固有频率和振动疲劳寿命，结果如表3所示。

表3 薄壁结构的固有频率和振动疲劳寿命比较

从表3可以看出：

(1) 试验测得的频率比模拟的频率略高，主要原因是因为试验过程中板的第一阶固有频率是通过施加1 g的正弦扫频载荷得到频率响应曲线，并且试验中的结构较薄，在振动过程中板的中央位置的振幅大于板的厚度，从而使板的几何刚度不容忽视，而有限元模拟采用壳单元，忽略了该项，试验中刚度项需附加上几何刚度，所以试验结果偏高。

(2) 不管是试验结果还是数值结果，加筋板的第一阶固有频率均高于不加筋板，这主要是由于筋的引入增加了结构质量，同时也提高了结构的刚度，并且刚度的增加程度远大于结构质量的增加。因此工程中常使用加筋板代替不加筋板，以获得高固有频率，延迟达到共振的时间。

(3) 对于振动疲劳寿命，试验得到的结果比数值模拟的结果偏低，主要原因是板在加工过程中存在内部缺陷或表面微裂纹，导致试验结果比模拟结果提前破坏；试验中三种板的疲劳寿命相差不大，考虑到三种板的加载频率均是在其本身共振带内，而两种加筋板的第一阶固有频率远高于不加筋板，所以从振动疲劳循环次数上看，两种加筋板的振动疲劳寿命明显高于不加筋板。

综上所述，利用有限元软件模拟得到试样的固有频率和试验结果误差在5%以内，验证了数值模拟的可靠性。由于振动疲劳试样结果分散性较大，业内认为模拟结果和试验结果在一个数量级即认为具有很好的吻合性，本文振动疲劳寿命试验和模拟误差在50%以内，说明本文采用的边界条件、数值模型和材料参数是合理的。

对于试验和模拟中的加筋板而言，T型加筋板的固有频率和振动疲劳寿命均高于L型加筋板。因此，有必要深入研究筋的不同截面形状对薄板的振动疲劳性能的影响，本文从有限元模拟角度来探讨筋的截面形状对薄壁结构的频率、应力和寿命的影响。

3 筋的不同截面形状对薄板振动疲劳性能的影响

3.1 有限元模拟

为了研究筋条的截面形状对薄板的振动疲劳性能的影响，对焊接了不同截面形状筋条的加筋板施加单频正弦压强载荷，载荷幅值为8 500 Pa，加载频率为加筋板的第一阶固有频率，边界条件分为四边固支与四边简支两种。加筋结构的平板尺寸为220 mm×220 mm×1.6 mm，板和筋的材料性能与1.1小节一致。筋的截面形状分为六种：矩形、L型、T型、I型、Z型、∏型。焊接于板上的两条筋间距为150 mm，且在板上对称分布。为保证所焊筋条的重量相等，六种筋的横截面面积相等且筋与板的接触面积相等，具体形状和尺寸如图7所示。首先对含有六种截面形状的加筋板进行模态分析，得到其模态频率；然后对各试样加载频带范围在其第一阶固有频率的0.8～1.2倍之间的幅值为10 g2/Hz的随机振动载荷谱，计算其应力及寿命值。

3.2 结果与讨论

3.2.1 对固有频率的影响

对于具有n自由度的线性阻尼振动系统，其运动微分方程为[13]

(2)

若忽略系统阻尼的影响，自由振动的运动微分方程表达为

(3)

设该方程的解为x=Φejwt，其中Φ为n阶振幅列阵，将其带入式(3)得到

K-ω2M=0

(4)

当系统发生振动时，式(4)为齐次线性方程组，具有非零解的条件为其系数矩阵的行列式等于零，即

|K-ω2M|=0

(5)

式(5)称为系统的特征方程，将其展开可获得以ω2为未知量的n次代数方程，求解得到n个ω2值，即系统的n个固有频率，由小到大排列，最小的称之为第一阶固有频率(基本频率)，其余依次为第二阶固有频率、第三阶固有频率等。通过式(5)可以求出任意结构的固有频率,对于任意给定结构，其固有频率的平方值与其质量成反比，与其刚度成反比。

对于质量相同、筋条截面形状不同的加筋板来说，在给定的边界条件下，结构刚度不同，其固有频率必然不同。四边固支和简支条件下，六种不同截面形状的加筋板结构的前三阶固有频率值如图8所示。

从图8可以看出：在固支条件下加筋板的第一阶固有频率值普遍高于在简支条件下的值，其根本原因在于固支条件下相应结构的边界约束较大，使得其结构刚度显著提高；在任何同一边界条件下，其第一阶固有频率值的关系为Z型>L型>T型>I型>∏型>矩形，这是因为在一阶模态下，结构承受抗弯刚度，而抗弯刚度取决于其在挠度方向的惯性矩[15]，经过计算六种截面形状的筋的惯性矩，得到其大小关系为Z型>L型>T型>I型>∏型>矩形，这与加筋板第一阶固有频率的大小关系一致。

3.2.2 对结构VonMises应力分布的影响

随机振动条件下，筋条在薄板的布局相同，因此在同样的边界条件，其VonMises应力分布云图基本不变。固支边界条件作用下，I型加筋板的VonMises应力分布云图如图9(a)所示，位置1、位置2和位置3分别是第一阶固有频率作用下出现局部应力最大值的位置。简支条件下，在第一阶固有频率时，加筋板的VonMises应力分布云图如图9(b)所示，局部应力最大值的位置分布出现在位置1、位置2和位置4。

从图1和图9可以看出：位置1在加筋板的中心位置，由于所加载荷频带处于第一阶固有频率的0.8～1.2倍的共振区域，中心区域的应变最大，而所研究的结构在线弹性范围内，因而在加筋板的中心区域出现了局部应力最大值；位置2在筋条连接在薄板位置的区域，局部质量增加易出现应力集中；固支条件下，位置3出现局部应力集中，而在简支条件下，局部应力集中现象没有出现在相应位置，而是出现在位置4，原因在于简支条件下，加筋板结构四周边界处可以转动，而筋条增加了局部刚度，阻碍了板的转动，因而在筋条与边界最近处位置4的位置出现应力集中；在简支条件下应力集中的区域位置1和位置2的范围都比在固支条件下的大，究其原因在于简支条件加筋板的四周边界处可以转动，使得其在振动条件下相应区域内发生形变更容易，沿面外方向的应变方向更大；特别在中心区域的应力值也更大，在位置1处，简支条件下加筋板的最大VonMises应力为174MPa，而在固支条件下其最大值仅为142MPa。

事实上，同样的加筋构型下，简支条件下的局部VonMises应力峰值一般大于固支条件下的峰值，四边固支/四边简支条件下加筋板的局部VonMises应力峰值如表4所示。

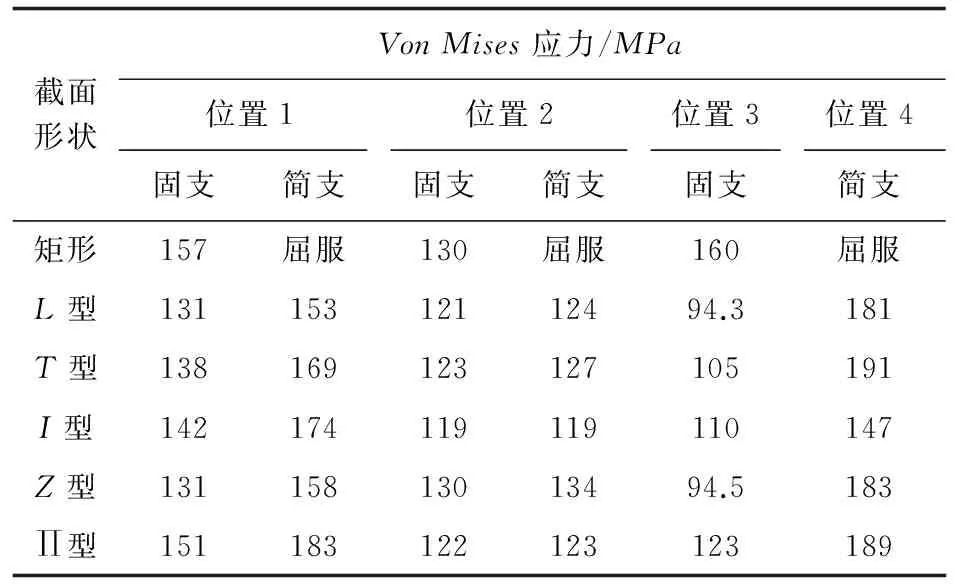
表4 四边固支和四边简支条件下加筋板的局部Von Mises应力

从表4可以看出：①在固支条件下，比较点焊不同截面形状筋条的加筋板局部应力峰值大小发现，位置1处的VonMises峰值最大，位置3处的VonMises峰值最小；②在简支条件下，位置4处的VonMises峰值最大，位置1处的VonMises峰值最小，这两种现象的出现，是由于边界约束条件和筋的耦合作用产生的；③在固支条件下，截面形状不同，其在中心区域位置1的局部VonMises值不同，其大小排序为矩形>∏型>I型>T型>Z型>L型，因为结构处于一阶共振频带内，其振动形式为沿着薄板法线方向上下振动，并且研究的结构是线弹性结构，其应力值与应变/位移成线性关系，故结构的抗弯刚度越大，其变形越小，其局部VonMises值越小，对于具有同样质量的加筋板来说，其固有频率越大，因而其中心区域的VonMises峰值大小排序正好与其第一阶固有频率大小关系相反；④含矩形截面筋条的加筋板结构在简支条件已达到屈服，这是因为其在简支条件下刚度太小。

3.2.3 对疲劳寿命的影响

大多数工程结构的振动疲劳失效往往是在一系列变幅循环载荷作用下产生疲劳损伤并累积而造成的。线性疲劳累积损伤理论是指材料或结构在循环载荷作用下，其疲劳损伤可线性累加，各个量级应力之间相互独立并且互不相关。当损伤累积到某一数值时，结构件就发生疲劳破坏。线性累积损伤理论中最经典和常用的是Palmgren-Miner理论，简称Miner理论[14]。

其表达式为

D=∑(ni/Ni)

(6)

式中：D为疲劳损伤；ni为某应力范围和平均应力下的循环次数；i为范围变量；Ni为该应力范围和平均应力下试样完全疲劳破坏所对应循环次数。

按照Miner线性疲劳损伤累积准则，当D=1时，试样完全疲劳失效破坏。根据Miner理论计算得到在不同边界和加筋构型条件下振动疲劳破坏区域和寿命值。四边简支的加筋板结构振动破坏位置在板的中央位置位置1，而四边简支的加筋板结构的振动疲劳破坏位置在板的左右两边位置，即位置3，如图9所示。具体不同构型加筋板的振动疲劳寿命如图10所示。

从图10可以看出：除了矩形筋外的五种筋条构型对板振动疲劳寿命的影响不随边界约束条件的不同而改变，其关系为L型>Z型>T型>I型>∏型，这与加筋板在破坏位置的应力大小关系相反，即破坏位置应力越大，寿命越短。

4 结 论

(1) 通过平板及加筋板的振动疲劳试验和有限元数值模拟结果的对比，验证了所采取模拟过程方法的准确性和可行性。

(2) 在筋条质量相等且与平板的接触面积相同的情况下，采用同样的边界条件，当筋条的截面挠度方向的惯性矩较大时，筋的抗弯刚度较大，则加筋结构的第一阶固有频率较大；相应地，若不同截面形状的加筋板结构在同样的外载荷作用下，筋条的截面惯性矩较大时，对应的加筋结构危险点处的应力会较小，则此种加筋结构的振动疲劳寿命会较长。

[1]LamYC,SanthikumarS.Automatedriblocationandoptimizationforplatestructures[J].Structural&MultidisciplinaryOptimization, 2003, 25(1): 35-45.

[2]LuoJ,GeaHC.Asystematictopologyoptimizationapproachforoptimalstiffenerdesign[J].StructuralOptimization, 1998, 16(4): 280-288.

[3]KrogLA,OlhoffN.Optimumtopologyandreinforcementdesignofdiskandplatestructureswithmultiplestiffnessandeigenfrequencyobjectives[J].Computers&Structures, 1999, 72(4-5): 535-563.

[4]BojczukD,SzteleblakW.Optimizationoflayoutandshapeofstiffenersin2Dstructures[J].Computers&Structures, 2008, 86(13-14): 1436-1446.

[5]KallassyA,MarcelinJL.Optimizationofstiffenedplatesbygeneticsearch[J].StructuralOptimization, 1997, 13(2): 134-141.

[6]FatemiJ,TrompetteP.Optimaldesignofstiffenedplatestructures[R].AIAA-2002-1672, 2002.

[7]CrandallSH,MarkWD.Randomvibrationinmechanicalsystems[M].NewYork:AcedemicPress,1963: 90-92.

[8]LiouHY,WuWF,ShinCS.Amodifiedmodelfortheestimationoffatiguelifederivedfromrandomvibrationtheory[J].ProbabilisticEngineeringMechanics, 1999, 14(3): 281-288.

[9] 王明珠, 姚卫星， 孙伟. 结构随机振动疲劳寿命估算的样本法[J]. 中国机械工程, 2008, 19(8): 972-975.WangMingzhu,YaoWeixing,SunWei.Sampleapproachforfatiguelifepredictionofstructuresunderrandomvibration[J].ChinaMechanicalEngineering, 2008, 19(8): 972-975.(inChinese)

[10] 张积亭, 周苏枫. 飞机典型构件振动疲劳寿命分析[J]. 机械科学与技术, 2002, 21(增刊): 3,16.ZhangJiting,ZhouSufeng.Analysisofvibrationfratiguelifeoftypicalaircraftcomponents[J].MechanicalScienceandTechnology, 2002, 21(S1): 3,16.(inChinese)

[11] 郭建平, 任康, 杨龙, 等. 基于MSC.Fatigue的电子设备随机振动疲劳分析[J]. 航空计算技术, 2008, 3(4): 48-50.GuoJianping,RenKang,YangLong,etal.FatigueanalysisonrandomvibrationofelectronicequipmentbasedonMSC.Fatiguesoftware[J].AeronauticalComputingTechnique, 2008, 3(4): 48-50.(inChinese)

[12] 陈安, 许飞, 闫文伟, 等. 基于DFR法的Al-Li-S4铝锂合金铆接结构[J]. 航空工程进展, 2016, 7(1): 101-105.ChenAn,XuFei,YanWenwei,et.al.FatiguereliabilityanalysisofAl-Li-S4rivetedjointsbasedondetailfatiguerating[J].AdvancesinAeronauticalScienceandEngineering, 2016, 7(1): 101-105.(inChinese)

[13] 方同, 薛璞. 振动理论及应用[M]. 西安： 西北工业大学出版社, 1998: 69-70.FangTong,XuePu.Theoryandapplicationofvibration[M].Xi’an:NorthwesternPolytechnicalUniversityPress, 1998: 69-70.(inChinese)

[14]MinerMA.Cumulativedamageinfatigue[J].AmericanSocietyofMechanicalEngineers-JournalofAppliedMechanics, 1945, 12(3): 159-164.

[15] 苟文选. 材料力学(Ⅱ)[M]. 北京： 科学出版社， 2010: 346-347.GouWenxuan.Strengthofmaterials(Ⅱ)[M].Beijing:SciencePress, 2010: 346-347.(inChinese)

(编辑：赵毓梅)

Effects of Stiffeners’ Cross Section Shape on Thin Walled Structures’Vibration Fatigue Property

Liu Shuangyan, Tu Yuqian, Miao Yinggang, Li Yulong

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Stiffeners’ cross section shape plays an important role on the vibration fatigue property of stiffened panels. The vibration tests of two kinds of stiffened panels are carried out. The stiffened panels with L-shaped stiffener and T-shaped stiffener are excited by base motion at the resonance frequency, respectively. The effects of different stiffeners’ shape on the frequency and vibration fatigue life of thin-walled structures are studied experimentally. The possible mechanism is analyzed theoretically and the test process is validated by MSC software. Based on the reasonable FEM simulation, the thin-walled stiffened panels are excited by a sinusoidal distributed load under two boundary conditions(fully clamped and simply supported) in MSC simulation. The effects of stiffeners with six shapes (rectangle, L-shape, T-shape, I-shape, Z-shape and ∏-shape) on the frequency, stress distribution and vibration fatigue life of thin walled structures are discussed. In addition, the predicted study on the life of stiffened panel are carried out. The results show that the first natural frequency of panel with Z-shaped stiffener is the maximum among all the configurations. The peak value of the stress occurred at the same position. When the edges of the panel are fully clamped, the damage position occurred at the two sides of the stiffener and the fatigue life of Z-shaped stiffened panels is the longest. When the edges of the panels are simply supported, the damage position occurred at the center region of the panels and the L-shaped stiffened panels had the longest life.

thin-walled stiffened structure; cross shape; natural frequency; Von Mises; vibration fatigue life

2016-12-12；

2016-12-23

陕西省科技研究发展攻关计划 (2009K01-39，2012GY2-26)

李玉龙,liyulong@nwpu.edu.cn

1674-8190(2017)02-190-09

V214.4+2; O346.2

A

10.16615/j.cnki.1674-8190.2017.02.011

刘双燕(1984-)，女，博士研究生。主要研究方向：金属薄壁结构抑振修补。

涂玉倩(1992-)，女，硕士研究生。主要研究方向：复合材料薄壁结构的屈曲分析。

苗应刚(1983-)，男，博士,讲师。主要研究方向：Hopkinson杆技术、聚合物力学行为及变形机理、本构方程。

李玉龙(1961-)，男，博士，教授。主要研究方向：飞行器结构抗坠毁设计、飞行器结构抗离散源撞击设计、极端环境下先进材料及结构的力学行为及其优化设计。