随机复合材料统计多尺度边界元算法研究
李义强,杨自豪,杨志强
(1.西北工业大学 理学院,西安 710072)(2.哈尔滨工业大学 航天学院,哈尔滨 150001)
随机复合材料统计多尺度边界元算法研究
李义强1,杨自豪1,杨志强2
(1.西北工业大学 理学院,西安 710072)(2.哈尔滨工业大学 航天学院,哈尔滨 150001)
热传输行为是空天飞行器热防护系统服役过程中的重要问题,研究随机复合材料的热传输机理,可为热防护系统材料与结构的一体化设计提供理论依据。针对随机复合材料的热传导问题,发展一种统计多尺度边界元算法,首先建立等效材料参数的统计多尺度分析模型,然后给出统计意义下等效参数的多尺度边界元预测算法,并通过与理论结果的对比来验证算法的有效性,最后研究微结构分布状态对陶瓷多孔材料等效导热系数的影响。结果表明:采用统计多尺度模型及多尺度边界元算法预测随机复合材料的热传导性能是有效的。
随机复合材料;热传导性能;统计多尺度边界元算法;等效导热系数
0 引 言
实际材料的微细观构造通常是模糊不清的,随机不确定性是很多天然/工程材料的固有属性。复合材料的增强相离散地分布于基体中,增强相的几何尺寸、空间方位等多具有随机分布的特征。随机复合材料是工程中常用的一类复合材料。面对不断增长的工程应用需求,如何有效表征随机复合材料的细观结构,如何定量描述复合材料的局部细观构造特征对材料宏观性能的影响,已成为材料科学与工程领域的重要课题。
针对随机复合材料的热传导性能预测问题,国内外已开展了诸多研究,例如,Eshelby等效夹杂方法[1]、Hashin-Shtrikman(HS)上下界法[2]、自洽场方法[3]和Mori-Tanaka理论[4]等,但上述平均意义下的方法都对真实的材料结构进行了较大程度的简化以减少计算量,并不能充分反映材料的真实微结构特征。随着计算机技术的发展,针对颗粒填充或多孔复合材料的热学性能模拟预测问题,以有限元分析为基础的数值方法采用了规则排布的单胞模型[5],但仍然存在较大程度的简化。然而,颗粒/多孔随机复合材料需要更加真实、复杂的微结构单胞模型以及快速有效的热学性能预测方法,以便能够更精确地描述材料的实际热学行为。
近年来,针对不同类型的复合材料及其结构,崔俊芝等[6-8]基于均匀化方法[9],发展了一系列高阶双尺度计算方法,成功地预测了复合材料结构的物理和力学性能。基于此,Guan Xiaofei等[10]、Cui Junzhi等[11-12]通过引入均匀随机样本单胞模型,提出了统计二阶双尺度分析方法及其有限元方法,用于预测颗粒或孔洞随机分布复合材料的物理和力学性能。由于随机样本单胞的分散性,为了获得更为准确的等效热学性能,需要大量取样计算等效导热系数并求均值。此外,在使用传统的有限元方法求解多尺度单胞模型时,由于颗粒或孔洞数量巨大、尺寸较小、结构复杂,极大地增加了有限元网格剖分的难度,并且为了更好地逼近单胞结构,需要数量巨大的有限元网格,导致极大的计算量。
与有限元方法不同,边界元算法只需要在边界和界面上进行网格剖分[13-14],单胞结构网格划分难度小、网格数目少,因此,边界元算法在求解随机复合材料单胞模型时具有明显优势。但是,边界元算法在直接求解复合材料物理力学问题时,存在诸多困难,特别是在求解三维问题时尚未有成熟的方法。本文针对多孔随机分布复合材料的热传导问题,发展一种统计多尺度边界元算法,并应用该方法计算复合材料结构的热学参数,分析其热学性能,以期为研究随机复合材料的热传输机理提供有益参考。
1 随机复合材料微结构表征
设随机复合材料结构Ω由颗粒和基体组成,将颗粒或孔洞的形状统一设为椭球或者嵌入椭球的多面体,并假设材料内部颗粒或孔洞的随机分布模型处处相同。在三维空间中,一个椭球可以由9个参数(椭球的中心点,长、中、短轴的长度和方向角)唯一确定。基于工程测量和统计方法,整个复合材料结构Ω可以逻辑地分为一系列具有相同尺寸ε的单胞体[15],如图1所示。
因此,只要确定一个单胞内椭球的概率分布模型,也就确定了整个复合材料结构的细观特征。按照上述表征方法,随机分布复合材料结构Ω可以看作是由具有相同颗粒或孔洞分布模型的单胞组合而成,即
(1)
式中:ε(Qs+zs)为区域Ω内的第s个单胞;P为复合材料的概率分布模型。
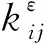
(2)
式中:ei为单胞εQs内的第i个椭球颗粒;A1和A2分别为颗粒和基体的材料参数。
2 统计多尺度分析模型
对于随机分布复合材料,考虑如下具有混合边界条件的稳态热传导问题:
(3)
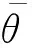
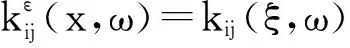
θε(x,ωs)= θ0(x,ξ,ωs)+εθ1(x,ξ,ωs)+
ε2θ2(x,ξ,ωs)+…
(4)
由于ξ=x/ε,存在如下链式法则:
(5)
将式(4)~式(5)带入式(3),并整理成ε幂级数形式,可得:
O(ε)=f
(6)
比较式(6)两端不同ε幂次的系数,通过偏微分方程理论可分别定义θ0,θ1和θ2,则温度场的多尺度渐进展开式可定义为

(7)
式中:θ0(x)为定义在Ω上的均匀化解;Hα1(ξ,ωs)和Hα1α2(ξ,ωs)为定义在单位化单胞Qs上的依赖于样本ωs的局部单胞解。
Hα1(ξ,ωs)是控制方程式(8)的解。
(8)
通过式(9)可得与样本ωs有关的均匀化热传导系数:
(9)
根据柯尔莫哥洛夫强大数定理,期望均匀化系数为
(10)

(11)
Hα1α2(ξ,ωs)是式(12)的解。
(12)
基于温度场的多尺度计算模型(式(7)),可以推导出热流密度的多尺度计算公式:
(13)
3 统计多尺度边界元算法
随机单胞结构十分复杂,为了有效求解单胞问题,采用有限元方法需要大量的体网格来逼近单胞结构,使得计算规模巨大。在统计多尺度分析模型中,计算期望均匀化系数时需要求解大量单胞问题,导致采用有限元方法时会产生巨大的计算量。与有限元方法不同,边界元算法只需要在单胞边界上进行离散,不需要体网格,有效地减小了计算规模,提高了计算效率。假设复合材料的基体和颗粒/孔洞的导热性质满足各向同性,本节将给出统计多尺度边界元算法及其计算流程。
3.1 单胞问题边界元算法
推导单胞函数Hα1(ξ,ωs)满足的式(8)的边界积分方程形式,该方程类似于Laplace方程,取其基本解为[13]
(14)
取kij(ξ,ωs)=k(ξ,ωs),并以基本解G(ξ,τ)为权函数,对式(8)进行加权积分,得:
(15)
利用高斯散度定理和基本解的性质[14],对式(15)的第一个积分项进行分部积分:
=-c(τ)k(τ,ωs)Hα1(τ,ωs)-
∫∂QsG(ξ,τ)q(ξ)dS-
(τ∈∂Qs)
(16)
因此,单胞函数Hα1(ξ,ωs)满足的积分方程为
-c(τ)k(τ,ωs)Hα1(τ,ωs)
∫QsG(ξ,τ)bα1(ξ)dξ-
(τ∈∂Qs)
(17)
其中,
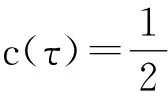
由于式(17)仍含有区域积分,需要做进一步处理。对于式(17)等号右端第三项,采用径向积分方法[14]可得:
(18)
式中:rα(p,ξ)为p点和ξ之间的距离,对于二维问题,α=2,对于三维问题,α=3。
再处理式(17)等号右端第四项,记:
(19)
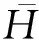
(20)
式中:Nj为全局插值函数;φi(ξ)为径向基函数;Φ为径向基函数插值矩阵。
再采用径向积分方法将上述区域积分转换为边界积分,即
(21)
综上所述,便可得到单胞函数所满足的边界积分方程。通过对单胞Qs的边界进行网格剖分,并进行边界单元插值,计算各项积分,得到线性代数方程组,求解可得单胞问题的数值解。
3.2 算法流程
基于统计多尺度边界元算法的随机复合材料热传导性能的算法流程为:
(1) 根据给定的概率分布模型P,生成一个随机样本单胞Q(ωs)(ωs∈P)[15],并对其进行网格剖分[16];
(2) 利用边界元算法求解单胞问题(式(8)和式(12));
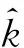
(4) 根据求解出的期望均匀化系数,求解均匀化问题(式(11)),得到宏观温度解θ0(x);
(5) 对应样本单胞Q(ωs),基于已求出的单胞函数解和宏观均匀化温度解,通过多尺度计算公式(式(7)和式(13)),可以分别确定单胞εQs内的温度场、热流密度场,还可以进一步计算出热流密度极值。
4 算例分析
为了研究随机复合材料的微观构造对材料宏观导热性能的影响,考虑三种微观孔洞分布状态:圆球孔洞中心均匀分布,圆球孔洞中心以单胞的形心点为中心正态分布,长椭球孔洞(长轴为中轴和短轴的2倍)的倾角沿x3方向正态分布,且中心在单胞内均匀分布,如图2所示。
由于孔洞分布的随机性,即使孔洞的分布模型完全相同,其数值计算结果也会因样本的不同而有所差别。为了得到较为准确的预测结果,必须进行大量样本计算,再计算出统计意义下的结果。本文的计算结果均为随机抽样50次统计所得。
当基体材料为陶瓷,导热系数为4.41 W/mK时,将采用统计多尺度边界元算法预测的期望均匀化导热系数与采用Hashin-Shtrikman(HS)上下界法的结果进行比较,结果如表1~表3所示。
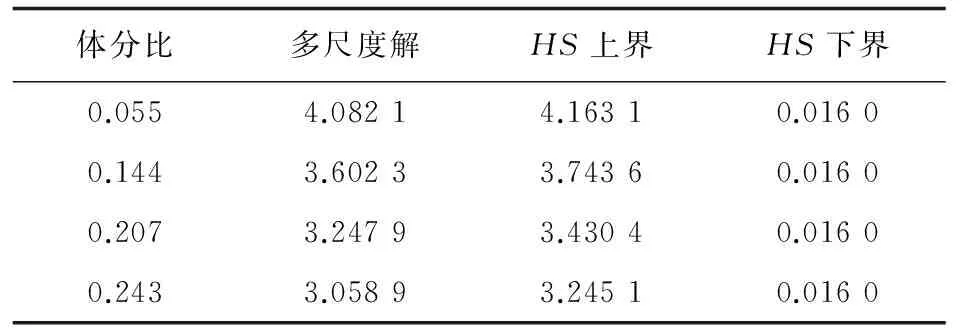
表1 圆球孔洞均匀分布不同体积分数时均匀化导热系数的多尺度解与HS界的比较
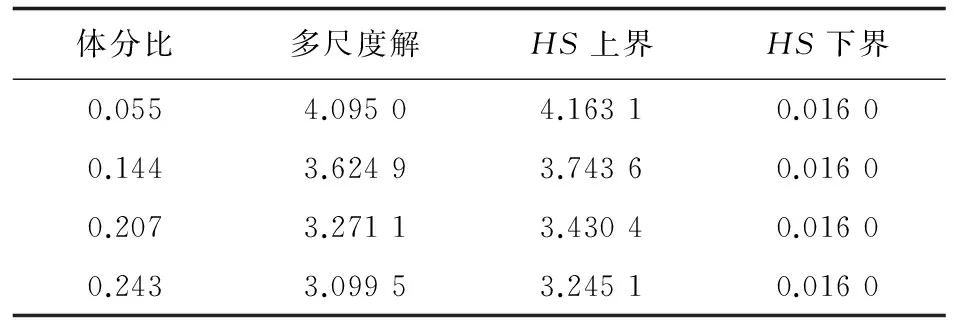
表2 圆球孔洞正态分布不同体积分数时均匀化导热系数的多尺度解与HS界的比较

表3 椭球孔洞倾角正态分布不同体积分数时均匀化导热系数的多尺度解与HS界的比较
从表1~表3可以看出:对于不同体积分数和分布状态的多孔随机分布复合材料,其多尺度数值解均在HS界内,且对于相同分布状态的复合材料结构,其宏观均匀化系数随孔洞体积分数的增大而发生较大变化,表明孔洞的体积分数、结构形态以及分布状态对复合材料的宏观等效导热性能具有重要影响。
多尺度有限元网格数目与多尺度边界元网格数目的比较如表4所示,可以看出:边界元网格的数目远少于有限元网格的数目,即采用多尺度边界元算法相比有限元方法可减少相当大的计算量,尤其是在大量取样计算过程中,采用边界元算法进行计算所节约的计算量是相当可观的。
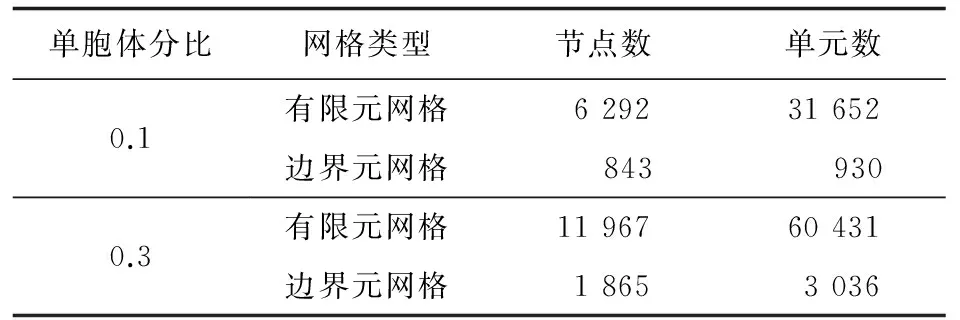
表4 有限元网格与边界元网格数比较
当选取陶瓷作为基体材料时,其导热系数为21.16W/mK时,取样一次,分别采用有限元方法和边界元算法计算出的均匀化系数如表5所示(两种算法的计算精度基本一致)。
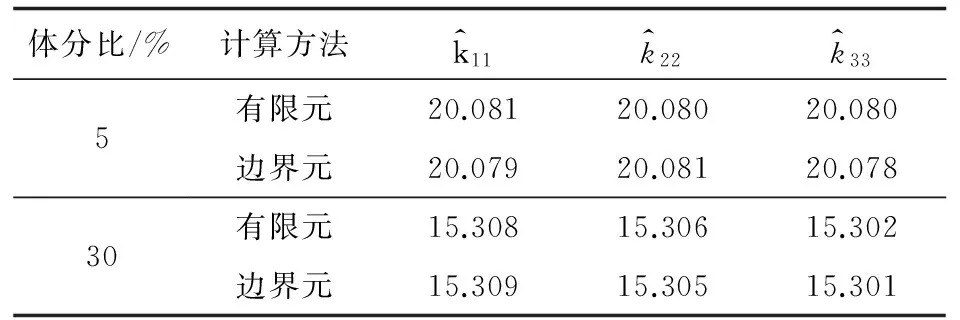
表5 圆球孔洞均匀分布时均匀化导热系数计算结果
从表4~表5可以看出:多尺度边界元算法仅用较少的时间就能得到满意的结果,是一种高效率、高精度的数值算法。
选取不同样本数量时的期望均匀化系数计算结果如图3所示,可以看出:计算结果的分散性随着样本数量的增加而减小。
5 结 论
(1) 本文采用多尺度边界元算法预测了多孔随机复合材料的等效导热系数,并将数值计算结果与理论值进行对比,表明多尺度边界元算法能够有效预测随机复合材料的宏观导热性能。
(2) 多孔随机复合材料的热传导性能不仅依赖于宏观条件,还与复合材料的细观结构有关,包括孔洞的体积分数、结构形态以及分布状态等,统计多尺度边界元算法能够较为准确地捕捉多孔随机复合材料的细观结构信息。
(3) 统计多尺度边界元算法在求解具有大量孔洞随机分布复合材料的热传导问题时,仅以较少的计算时间就能得到满意的结果,是一种高效率、高精度的数值算法。
[1]EshelbyJD.Thedeterminationoftheelasticfieldofanellipsoidalinclusion,andrelatedproblems[J].ProceedingsoftheRoyalSocietyofLondon, 1957, 241(2): 376-396.
[2]HashinZ,ShtrikmanS.Avariationalapproachtothetheoryoftheelasticbehaviourofmultiphasematerials[J].JournaloftheMechanicsandPhysicsofSolids, 1963, 11(2): 127-140.
[3]HillRW.Theelasticbehaviorofacrystallineaggregate[J].ProceedingsofthePhysicalSociety, 1952, 65(5): 349-354.
[4]MoriT,TanakaK.Averagestressinmatrixandaverageelasticenergyofmaterialswithmisfittinginclusions[J].ActaMetallurgica, 1973, 21(5): 571-574.
[5]KangGuozheng,ShaoXuejiao,GuoSujuan.EffectofinterfacialbondingonuniaxialratchettingofSiCP/6061Alcomposites:finiteelementanalysiswith2-Dand3-Dunitcells[J].MaterialsScienceandEngineering:A, 2008, 487(1/2): 431-444.
[6] 崔俊芝, 曹礼群. 基于双尺度渐进分析的有限元算法[J]. 计算数学, 1998, 20(1): 89-103.CuiJunzhi,CaoLiqun.Finiteelementmethodbasedontwo-scaleasymptoticanalysis[J].MathematicaNumericaSinica, 1998, 20(1): 89-103.(inChinese)
[7]YangZihao,CuiJunzhi,WuYatao,etal.Second-ordertwo-scaleanalysismethodfordynamicthermo-mechanicalproblemsinperiodicstructure[J].InternationalJournalofNumericalAnalysis&Modeling, 2015, 12(1): 144-161.
[8]CuiJunzhi,YuXingang.Atwo-scalemethodforidentifyingmechanicalparametersofcompositematerialswithperiodicconfiguration[J].ActaMechanicaSinica, 2006, 22(6): 581-594.
[9]BensoussanA,LionsJL,PapanicolaouG.Asymptoticanalysisforperiodicstructures[M].Amsterdam:North-HollandPublishingCompany, 1978.
[10]GuanXiaofei,LiuXian,JiaXin,etal.Astochasticmultiscalemodelforpredictingmechanicalpropertiesoffiberreinforcedconcrete[J].InternationalJournalofSolidsandStructures, 2015, 56/57: 280-289.
[11]YangZihao,CuiJunzhi.Thestatisticalsecond-ordertwo-scaleanalysisfordynamicthermo-mechanicalperformancesofthecompositestructurewithconsistentrandomdistributionofparticles[J].ComputationalMaterialsScience, 2013, 69: 359-373.
[12]LiYouyun,CuiJunzhi.Themulti-scalecomputationalme-thodforthemechanicsparametersofthematerialswithrandomdistributionofmulti-scalegrains[J].CompositesScienceandTechnology, 2005, 65(9): 1447-1458.
[13] 姚振汉, 王海涛. 边界元法[M]. 北京: 高等教育出版社, 2010.YaoZhenhan,WangHaitao.Boundaryelementmethod[M].Beijing:HigherEducationPress, 2010.(inChinese)
[14] 高效伟, 王静, 彭海峰, 等. 高等边界单元法——理论与程序[M]. 北京: 科学出版社, 2015.GaoXiaowei,WangJing,PengHaifeng,etal.Advancedboundaryelementmethod:theoryandprogramm[M].Beijing:SciencePress, 2015.(inChinese)
[15]YuYan,CuiJunzhi,HanFei.Aneffectivecomputergenerationmethodforthecompositeswithrandomdistributionoflargenumbersofheterogeneousgrains[J].CompositesScienceandTechnology, 2008, 68(12): 2543-2550.
[16] 韩非. 随机复合材料力学性能预测的二阶双尺度方法[D]. 西安: 西北工业大学, 2010.HanFei.Thesecond-ordertwo-scalemethodforpredictingmechanicalperformanceofrandomcompositematerials[D].Xi’an:NorthwesternPolytechnicalUniversity, 2010.(inChinese)
(编辑:马文静)
Research on Statistical Multiscale Boundary Element Algorithm for Random Composite Materials
Li Yiqiang1, Yang Zihao1, Yang Zhiqiang2
(1.School of Natural and Applied Sciences, Northwestern Polytechnical University, Xi’an 710072, China)(2.School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
Random uncertainty is the inherent attribute of natural and engineering materials; the heat conduction behavior is one of the most important problems in servicing process of thermal protection system, and the research on the heat conduction problem of random composite materials can provide theoretical basis for integrative design of material and structure in thermal protection system. A novel statistical multiscale analysis method based on two-scale asymptotic expansions is proposed to predict heat conduction performances of random porous materials. The statistical multiscale formulations and statistical multiscale boundary element algorithm are brought forward. Besides, the validity of the proposed method by comparison with theoretical results is verified. Finally, the effect of microstructures on the macroscopic thermal properties for the porous ceramic materials is investigated. Numerical results prove the accuracy and efficiency of our method for multiscale simulation of heat conduction problem in random porous materials.
random composite materials; heat conduction performance; statistical multiscale boundary element algorithm; effective conduction parameter
2017-02-24;
2017-03-29
国家自然科学基金(11471262,11501449)
李义强,liyiqiang@mail.nwpu.edu.cn
1674-8190(2017)02-199-07
TB33
A
10.16615/j.cnki.1674-8190.2017.02.012
李义强(1984-),男,博士研究生。主要研究方向:边界元方法、并行计算。
杨自豪(1987-),男,博士,讲师。主要研究方向:复合材料多尺度分析方法。
杨志强(1984-),男,博士,副教授。主要研究方向:复合材料多尺度分析方法。

