基于改进萤火虫算法的结构损伤识别*
胡磊, 吕中荣, 刘济科
(中山大学工学院,广东 广州 510006)
基于改进萤火虫算法的结构损伤识别*
胡磊, 吕中荣, 刘济科
(中山大学工学院,广东 广州 510006)
提出一种基于改进萤火虫算法的结构损伤识别方法。将结构损伤模拟成杨氏模量的减少。对于没有邻居的萤火虫,让它们在自身位置附近随机搜索,同时引入新的移动方式来提高算法的精度和收敛速度,避免算法过早的陷入局部最优,克服萤火虫算法在高维目标函数中寻优能力不足的问题。采取功能梯度梁(Axial functionally graded, AFG)作为研究对象,利用欧拉-伯努利梁单元建立力学模型。采用了简支梁作为算例,将结果和基本萤火虫算法、领导者萤火虫和自适应步长萤火虫算法作对比,说明改进的有效性。
损伤识别;萤火虫算法;功能梯度梁;高维目标函数
功能梯度梁有着出色的力学和热学性能,被广泛应用于各个领域,例如空间和平面桁架,航天器的热防护盾等[1-3]。由于功能梯度梁被应用于各种各样恶劣的环境中,对于它们的结构损伤识别显得尤为重要。
结构损伤识别主要分为时域和频域两种。频域法主要根据结构的固有频率、模态、柔度曲率、模态能量等数据去识别损伤[4-7]。而时域法直接利用结构的动力响应如加速度[8-9],Law等[10]利用时域法检测了移动车辆荷载下的混凝土桥梁损伤。具有一定的工程应用价值。
近年来,由于计算机技术的发展,出现了许多群智能算法,如粒子群算法,遗传算法,人工蜂群算法等。这些算法被用来解决各种复杂的优化问题。利用结构的频率或者动力响应,建立结构的目标函数,可以将结构损伤问题看成一个优化问题。萤火虫算法作为一种模拟萤火虫发光的群智能算法[11]。由于它优异的鲁棒性已被应用于各种各样的领域[12-14]。但涉及到结构损伤检测领域的研究很少,本文基于改进萤火虫算法,识别功能梯度梁的结构损伤。通过对没有邻居的萤火虫加入扰动,同时在萤火虫移动阶段引入新的移动方式来提高算法的收敛速度和精度。最终的结果说明改进策略极大的增强了萤火虫算法在高维目标函数中的寻优能力,数值算例表明在无噪声和有噪声的情况下均可以精确的识别损伤。
1 力学模型
1.1 完整和损伤的AFG梁有限元建模
设有一长为L,宽为b,高为h的功能梯度梁,杨氏模量E和密度ρ沿着梁的轴向连续变化,变化方程可表示为:
E(x)=(EL-ER)(1-x/L)ϑ+ER
(1)
ρ(x)=(ρL-ρR)(1-x/L)ϑ+ρR
(2)
其中EL和ER分别为梁左端和右端的杨氏模量,ρL和ρR为左端和右端的密度。ϑ为一个非负的常数。
梁离散化的振动方程为

(3)

当梁有损伤时,假定损伤只会影响梁的刚度参数(如杨氏模量)而不会影响质量, 用一组无量纲的常数α表示损伤程度,则损伤梁的杨氏模量如下:
E=E0(1+α), with-1≤α≤0
(4)
假设ith单元损伤,则它的单元刚度矩阵为
(5)
总体刚度矩阵可由单元刚度矩阵集成得到。
1.2 目标函数
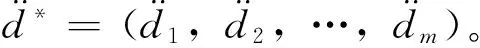
(6)
其中nt为测量时间点,m为测点个数。则识别问题转换为一个优化问题。找到一组α,使得计算出来的目标函数值最小。
2 识别算法
2.1 萤火虫算法
萤火虫算法(glowwormswarmoptimizationGSO)是一种根据萤火虫发光行为而提出的优化算法[14],每一只萤火虫代表一组可能的解,萤火虫的发光亮度取决它所处的位置,愈亮的萤火虫拥有愈高的吸引力,可以吸引它周围的萤火虫朝自身移动,从而得到最优解。萤火虫算法的具体算法在许多文献中都有提及[16-17],本文不再赘述。
2.2 改进萤火虫算法。
在基本GSO算法中,步长是固定的,这会导致收敛的效率低,结果精度差。
黄凯等[16]提出了一种自适应变步长的萤火虫算法(VSAGSO),步长公式为:
s=s0exp(-30(t/Tmax)p)+smin
(7)
其中s0为初始步长,smin为最小步长,Tmax为最大迭代次数,p为常数。
同时为了加快萤火虫的收敛速度,Zhou等[17]引入了领导机制(LeaderGSO),在算法每次迭代前找到位置最优的萤火虫设置为领导者,每次迭代结束后,所有萤火虫均向领导者所在位置移动。移动公式如下:
xi(t)=xt(t)+rand·(xleader(t)-xi(t))
(8)
但是这些改进并不能使得萤火虫算法能应用于损伤识别问题的优化中,因为损伤识别的优化问题是一个高维的优化问题。GSO算法在高维空间的目标函数优化能力上比较差,本文基于上述的改进,对算法进行深入研究,提出改进策略。发现GSO算法在移动阶段,没有邻居的萤火虫(这个萤火虫是最亮的,或者它的决策域内没有萤火虫)不会更新它的位置,这浪费了大量的资源,因此提出让没有邻居的萤火虫在自己周围随机扰动,扰动公式如下:
xi(t)=xi(t)(1+2exp(-30×(t/Tmax)P)·
(2rand-1)
(9)
同时为了更好的加快收敛速度,在所有萤火虫向领导者移动一步之后,我们只更新移动后位置优于移动之前的。
3 数值算例
3.1 测试函数
为了说明改进的有效性,本文采取4个标准测试函数对算法进行测试,如表1所示。
实验参数选取如下:萤火虫数量选取为100,迭代1 000次。算法参数选择为:ρ=0.4,γ=0.6,β=0.8,l0=5,nt=10,s=0.3,rs=5。对于每个测试函数独立运算10次,分别取最优值、最差值和均值进行对比,结果如表2所示。

表1 标准测试函数Table 1 Standard test functions

表2 标准测试函数试验结果对比Table 2 Comparison of standard test function results
从表2可以看出本文的改进算法无论是在单峰还是多峰的测试函数中均表现良好,对比另外两个改进策略,最差的Griewank函数也有3到5个数量级的提升,最好的Sphere函数有将近20个数量级的提升。同时可以看出,在多维函数的测试中,本文的改进算法均能寻找到最优解,而LSGO和VSAGSO除第一个测试函数外,都没能找的最优解。说明改进策略解决了萤火虫算法在高维目标函数中识别效果不佳的问题。
3.2 损伤识别
梁的长度L=2 m,宽d=0.05 m,高h=0.025 m。梁的左端为铁,杨氏模量El=206 GPa,密度ρl=7 800 kg/m3。右端为铝,杨氏模量Er=70 GPa,密度ρr=2 700 kg/m3。常数ϑ=0.5。假设梁上有两处损伤,算法参数除rs=0.88外,其余参数选择同工况一。Newmark法的时间步长选为0.002s,截取0~1.5s的数据。识别结果如图1、图2所示。
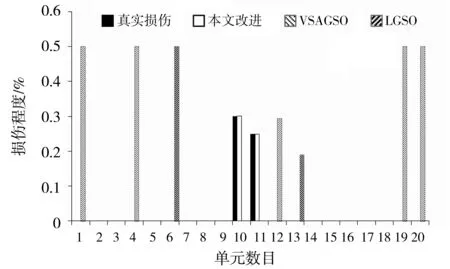
图1 双损伤、无噪声识别结果Fig.1 Damage identification results (double damage, noise free)

图2 双损伤、10%噪声识别结果Fig.2 Damage identification results (double damage, 10% noise level)
从图1和图2的识别结果可以看出,在没有噪声的情况下,本文的改进方法能准确的识别损伤参数。即使在10%噪声的情况下,改进方法依然能非常准确的识别出桥梁的损伤,两处损伤的最大误差也只有4.26%,同时出现的误判几乎可以忽略不计。而另外两种改进策略在两种情况下均未能成功识别损伤,陷入局部最优。
4 结 论
本文基于已有的改进策略,提出了一种新的萤火虫改进算法。克服了萤火虫算法在高维目标函数中寻优能力不足的问题。数值算例的结果表明,改进算法的寻优能力强、计算精度高,在实际工程中具有一定的应用价值。
[1]JHADK,KANTT,SINGHRK.Acriticalreviewofrecentresearchonfunctionallygradedplates[J].CompositeStructures, 2013,96:833-849.
[2]YINGJ,LUCF,CHENWQ.Two-dimensionalelasticitysolutionsforfunctionallygradedbeamsrestingonelasticfoundations[J].CompositeStructures, 2008,84(3):209-219.
[3]KAPURIAS,BHATTACHARYYAM,KUMARAN.Bendingandfreevibrationresponseoflayeredfunctionallygradedbeams:atheoreticalmodelanditsexperimentalvalidation[J].CompositeStructures, 2008,82(3):390-402.
[4]CHINCHALKARS.Determinationofcracklocationinbeamsusingnaturalfrequencies[J].JournalofSoundandVibration, 2001, 247(3):417-429.
[5]DILENAM,DELL’OSTEMF,MORASSIA.Detectingcracksinpipesfilledwithfluidfromchangesinnaturalfrequencies[J].MechanicalSystemsandSignalProcessing, 2011, 25(8):3186-3197.
[6]LUZR,LAWSS.Featuresofdynamicresponsesensitivityanditsapplicationindamagedetection[J].JournalofSoundandVibration, 2007,303(1/2):305-329.
[7] 杨秋伟,刘济科.结构损伤识别的柔度灵敏度方法[J].中山大学学报(自然科学版),2010,49(1):16-19.YANGQW,LIUJK.Damageidentificationbythesensitivityanalysisofstructuralflexibility[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2010,49(1):16-19.
[8]CHENJ,LIJ.Simultaneousidentificationofstructuralparametersandinputtimehistoryfromoutput-onlymeasurements[J].ComputationalMechanics,2004,33(5): 365-374.
[9]SHITH,JONESNP,ELLISJH.Simultaneousestimationofsystemandinputparametersfromoutputmeasurements[J].JournalofEngineeringMechanics, 2000,126 (7):746-753.
[10]LAWSS,ZHUXQ.Damagedetectioninconcretebridgestructuresundermovingvehicularloads[J].JournalofVibrationandAcoustics, 2007,129(1):58-65.
[11]KRISHNANANDKN,GHOSED.Detectionofmultiplesourcelocationsusingaglowwormmetaphorwithapplicationstocollectiverobotics[C].SwarmIntelligenceSymposium, 2005:84-91.
[12]WANGJ,CAOY,LIB,etal.Aglowwormswarmoptimizationbasedclusteringalgorithmwithmobilesinksupportforwirelesssensornetworks[J].JournalofInternetTechnology, 2015,16(5):825-832.
[13]ZHENOY,YINGL.Glowwormswarmoptimizationandmatchingpursuitsparsedecompositionforecologicalenvironmentalsoundsidentification[J].ComputerEngineeringandApplications, 2015,51(2):198-204.
[14]YEPESV,MARTIJV,GARCIA-SEGURAT.CostandCO2emissionoptimizationofprecast-prestressedconcreteU-beamroadbridgesbyahybridglowwormswarmalgorithm[J].AutomationinConstruction, 2015,49:123-134.
[15]ALSHORBAGYAE,ELTAHERMA,MAHMOUDFF.Freevibrationcharacteristicsofafunctionallygradedbeambyfiniteelementmethod[J].AppliedMathematicalModelling, 2011, 35(1):412-425.
[16] 黄凯,周永权.一种改进的变步长自适应GSO算法[J].计算机工程,2012,38(4):185-187.HUANGK,ZHOUYQ.ImprovedvariationstepadaptiveGSOalgorithm[J].ComputerEngineering, 2012,38(4):185-187.
[17]ZHOUY,LIUJ,ZHAOG.Leaderglowwormswarmoptimizationalgorithmforsolvingnonlinearequationssystems[J].PrzegladElektrotchniczny, 2012, 88(1):101-106.
Damage identification based on improved GSO algorithm
HULei,LÜZhongrong,LIUJike
(School of Engineering, Sun Yat-sen University,Guangzhou 510006,China)
An approach based on improved glowworm swarm optimization (GSO) for structure damage detection is presented. The local damage is simulated by a reduction in the elemental Young’s modulus of the beam .In order to enhance accuracy and convergence rate, the perturbation of the glowworm without neighbor is offered and a new search strategy is introduced in the movement phase of GSO to avoid local optima and enhance the GSO algorithm in high dimensions space target function optimization question solution ability. On the other hand, Axial functionally graded (AFG) beam with the assumptions of Euler-Bernoulli beam theory is adopted to establish the dynamic equation. The numerical experiments with a simply supported beam is carried to illustrate the efficiency of the proposed improvement GSO. The result reveals that the proposed method is more accurate compared to the original GSO, leader GSO (LGSO),and the variation step adaptive GSO.
damage identification; glowworm swarm optimization; axial functionally graded (AFG) beam; high dimensional objective function
2016-07-15 基金项目:国家自然科学基金(11572356);广东省自然科学基金(2015A030313126);广东省科技计划项目(2016A020223006)
胡磊(1992年生),男;研究方向:结构损伤识别;E-mail:hulei_mechanic@163.com
吕中荣(1975年生),男;研究方向:结构损伤识别;E-mail: lvzhr@mail.sysu.edu.cn
10.13471/j.cnki.acta.snus.2017.02.011
TP273
A
0529-6579(2017)02-0062-04

