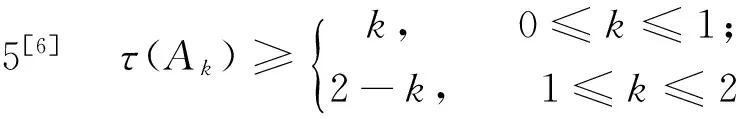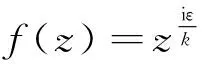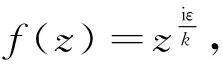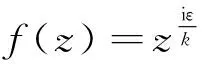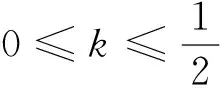平面区域的对数导数单叶性内径*
刘浔冰,刘雅萍,杨宗信
(江西师范大学数学与信息科学学院, 江西 南昌 330022)
平面区域的对数导数单叶性内径*
刘浔冰,刘雅萍,杨宗信
(江西师范大学数学与信息科学学院, 江西 南昌 330022)
研究了对数导数意义下平面区域的单叶性内径,讨论了对数导数意义下单叶性内径的相关性质,得到了角域的对数导数单叶性内径的上界估计。
对数导数;单叶性内径;万有Teichmüller空间
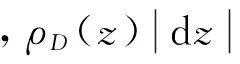
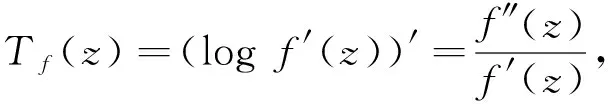
定义区域D的对数导数单叶性内径τ(D)为
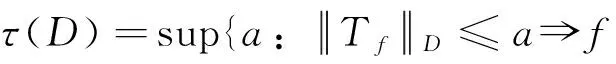
类似地,对于区域D内局部单叶的解析函f,可以定义f的Schwarz导数
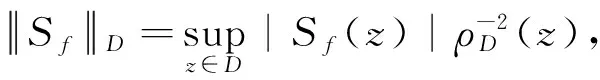
在D内单叶}
Becker[1]最早得到了对数导数与函数单叶性的关系,然后,Becker-Pommerenke[2]研究了单位圆内局部单叶的解析函数的对数导数与拟共形延拓的关系。1986年,Zhuravlev[3]及Astala-Gehring[4]建立了对数导数意义下的万有Teichmüller空间模型,激起了许多研究者的浓厚兴趣,人们首先想到的是与Schwarz导数意义下的Bers嵌入的万有Teichmüller空间模型进行对比研究。
可是,对数导数所涉及的条件远比Schwarz导数的条件弱,所以,两种万有Teichmüller空间模型之间虽有一些类似性质,但在某些性质上也有巨大差别。例如,Schwarz导数万有Teichmüller空间是连通的,而对数导数万有Teichmüller空间却有无穷多个分支;Schwarz导数单叶性内径取得最大值的区域只有圆域和半平面,而对数导数单叶性内径取得最大值的区域可以是除圆域和半平面以外的凸区域。
关于区域的Schwarz导数单叶性内径的精确值,已知的结果包括圆域(半平面)、角域、正多边形区域、菱形、某些矩形和某些等角六边形区域,所有这些结果都建立在与角域进行比较的基础上再根据Schwarz导数的范数在Möbius变换下的不变性而得到的。
对数导数的范数仅在仿射变换下保持不变,目前只知道任何边界多于两点的单连通区域D有τ(D)≤1。Astala-Gehring[4]证明了当且仅当D是拟圆时τ(D)>0。Stowe[5]证明了:当D为凸区域时,τ(D)≤1;当区域D非凸时,τ(D)<1。程涛等通过构造拟共形反射等方法给出了某些区域的对数导数单叶性内径的下界估计[4-12]。
由于得不到角域的对数导数单叶性内径的精确值,所以不能像研究Schwarz导数单叶性内径那样通过区域的核收敛来得到单叶性内径的上界和下界。我们研究对数导数范数的性质,并用于估计单叶性内径。
设f,g是区域D内局部单叶的解析函数,h是区域G到区域D上的共形映射,则ρG=(ρD∘h)|h′|,由
即
Tf∘h(z)=Tf(h(z))·h′(z)+Th(z)
(1)
Tf∘h-Tg∘h=(Tf∘h-Tg∘h)h′
从而有
‖Tf-Tg‖D=‖Tf∘h-Tg∘h‖G
特别地,若g=h-1是区域D上的共形映射,则由此可得
再令f为恒等映射,则有
当g=h-1是区域D上的仿射变换时,有
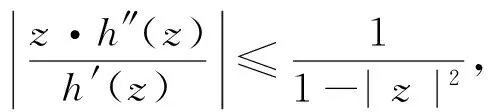
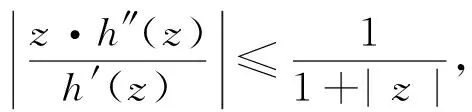
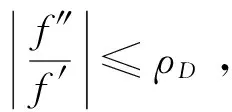
由引理1可知g在B内单叶,从而f在区域D=h(B)内单叶,即τ(D)=τ(h(B))≥1。
注1 当h满足h′(0)≠0,且有
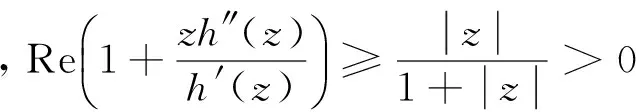
1 凸区域
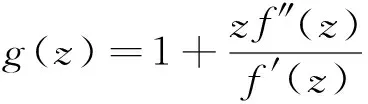
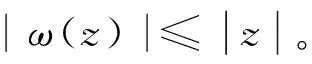
其中φ(z)在单位圆B内解析且|φ(z)|≤1。
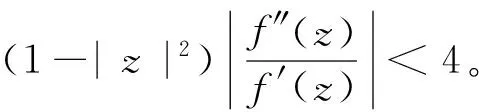
证明 对于z∈B,由于|ω(z)|≤|z|<1,有|1-ω(z)|≥1-|ω(z)|≥1-|z|>0,所以
从而
因此,

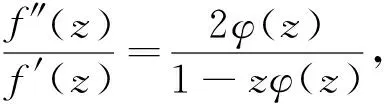
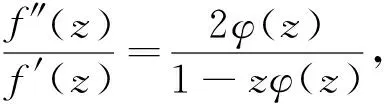
从而有
所以
是凸区域。
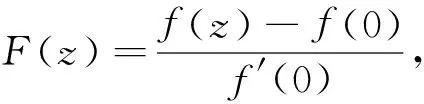
仍用f记规范化后的函数F。设f将圆周|z|=r<1映为曲线Cr,(见文[8],P43),由
可得
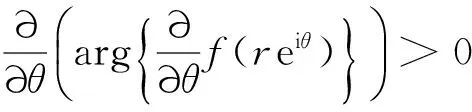
即曲线Cr上的切方向与正实轴的夹角是严格单调递增的。当一点z沿Cr正向绕行一周时,切方向与正实轴的夹角增量为
因此,Cr是包围凸区域的一条简单闭曲线。由|z|=r<1的任意性,f是单位圆B内的共形映照。
2 正n边形区域
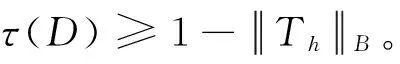
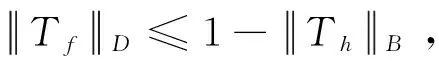
定理4 设Pn为正n边形区域,则τ(Pn)≥1-4/n。
证明 作单位圆盘B到正n边形区域Pn上的共形映射
通过计算得

首先,
其次,由
可知
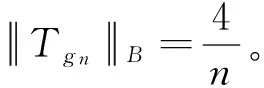
注3 当n=3,4时,结果是平凡的;当n→∞时,τ(Pn)→1。
3 角域Ak
引理3[5]若D是凸区域,则τ(D)≤1。
引理4[5]若D为非凸区域,则τ(D)<1。
利用复合函数对数导数的范数表达式,通过估计Riemann映射的对数导数的范数,我们给出单连通区域的对数导数单叶性内径的下界估计。
对于角域Ak={z:0 由此我们可以得到τ(Ak)的一个上界。 引理6τ(Ak)≤2k。 令z=reiθ,则容易算得(也可由文[7],P123),有 所以 由引理3-6,我们得到角域Ak的对数导数单叶性内径的一个估值。 [1]BECKERJ.LöwnerscheDifferentialgleichungandquasikonformfortsetzbareschlichteFunktionen[J].JReineAngewMath, 1972, 255: 23-43. [2]BECKERJ,POMMERENKEC.SchlichtheiskriterienandJordangebiete[J].JReineAngewMath, 1984, 354:74-94. [3]ZHURAVLEVIV.ModeloftheuniversalTeichmüllerspace[J].SibMathJ, 1986, 27: 691-697. [4]ASTALAK,GEHRINGFW.Injectivity,theBMOnormandtheuniversalTeichmüllerspace[J].JAnalyseMath, 1986, 46: 16-57. [5]STOWED.Injectivityandthepre-Schwarzianderivative[J].MichigenMathJ, 1998, 45: 537-546. [6] 程涛,程纪修. 区域的对数导数单叶性内径[J]. 中国科学(A辑),2007, 37(4): 504-512.CHENGT,CHENGJX.Theinnerradiusofunivalencybylogarithmicderivative[J].ScienceinChina(SeriesA), 2007, 37(4): 504-512. [7]LEHTOO.UnivalentfunctionsandTeichmüllerspaces[M].NewYork:Springer-Varlag, 1987. [8]DURENP.Univalentfunctions[M].NewYork:Springer-Varlag, 1983. [9] 郭辉,冯小高,崔泽建. 基于角域对数导数意义下的单叶性内径[J]. 深圳大学学报(理工版),2008, 25(4): 437-440.GUOH,FENGXG,CUIZJ.Theinnerradiusofunivalenceinthesenseofpre-Schwarzianderivativebasedonangulardomain[J].JournalofShenzhenUniversity(Science&Engineering), 2008, 25(4): 437-440. [10] 程涛,石艳. 基于任意拟圆的对数导数意义下区域的单叶性内径[J]. 南昌大学学报(理科版),2009, 33(3): 219-223.CHENGT,SHIY.TheInnerradiusofunivalenceinthesenseofpre-Schwarzianderivativebasedonanyquasidisk[J].JournalofNanchangUniversity(NaturalScience), 2009, 33(3): 219-223. [11] 张思汇,陈纪修. 以无穷远为内点的平面区域的单叶性内径(英文)[J]. 复旦学报(自然科学版),2011, 50(6): 689-695.ZHANGSH,CHENJX.Ontheinnerradiusofunivalencyofplanedomainscontainingthepoint∞ [J].JournalofFudanUniversity(NaturalScience), 2011, 50(6): 689-695. [12]PONNUSAMYS,SAHOOSK,SUGAWAT.Radiusproblemsassociatedwithpre-SchwarzianandSchwarzianderivatives[J].Mathematics, 2012, 34(2):163-172. On the inner radius of univalency by pre-Schwarzian derivative LIUXunbing,LIUYaping,YANGZongxin (School of Mathematics and Informatics, Jiangxi Normal University, Nanchang 330022, China) The inner radius of univalency of hyperbolic domains by pre-Schwazian derivative is studied, Some properties for the norm of pre-Schwarzian derivative and inner radius are established. As an application, the bounds of inner radius for angular domains are obtained. pre-Schwarzian derivative; inner radius of univalency; universal Teichmüller space 2016-06-15 基金项目:国家自然科学基金(11261022) 刘浔冰(1995年生),女;研究方向:函数论;E-mail:ashnilx@ 163.com 杨宗信(1966年生),男;研究方向:复分析;E-mail:yangzxn@ 163.com 10.13471/j.cnki.acta.snus.2017.02.009 O A 0529-6579(2017)02-0053-04