变量核奇异积分算子在加权(Lq,Lp)α(Rn)空间上的有界性
邵旭馗,王素萍
(陇东学院数学与统计学院,甘肃庆阳745000)
变量核奇异积分算子在加权(Lq,Lp)α(Rn)空间上的有界性
邵旭馗,王素萍
(陇东学院数学与统计学院,甘肃庆阳745000)
利用Ap权性质,研究了带变量核的奇异积分算子TΩ在加权共合空间(Lq,Lp)α(Rn)上的性质,证明了TΩ是(Lq,Lp)α(Rn)空间上的有界算子。
奇异积分算子; 加权(Lq,Lp)α(Rn)空间;变量核
1955 年,Calderon 和Zygmund[1]考虑了带变量核的奇异积分算子的Lp有界性,他们发现这类算子同带有变系数的二阶线性椭圆方程密切相关,有关此类算子的有界性可见文献[2-3]。 近年来,关于带变量核的奇异积分算子的有界性受到人们的广泛关注, 2002 年,Ding,Chen和Fan[4]考虑了带变量核的奇异积分算子的(Hp,Lp) 有界性,得到了当Ω在Sn-1上满足一类Lr-Dini(r≥1) 条件时,对某些p≤1,TΩ是Hp到Lp的有界算子,2006 年,Ding,Lu和Shao[5]研究了TΩ(f)在弱Hardy空间上的有界性, 有关变量核奇异积分算子及其交换子的结果可参见文[6-8]。最近,Wu,Cheng和Shu[9]又得到了粗糙核奇异积分算子TΩ在加权(Lq,Lp)α(Rn)空间上的估计。受以上研究的启发,本文考虑并证明了当带变量核的奇异积分算子TΩ(f)在加权(Lq,Lp)α(Rn)空间上的有界性,从而推广了以往非变量核的相关结果。
1 预备知识及主要结果
记Sn-1为Rn(n≥2)中的单位球面,其上装备了Lebesgue测度dσ=dσ(z′)。设定义在Rn×Rn上的函数Ω∈L∞(Rn)×Lr(Sn-1)(r≥1), 满足:
‖Ω‖L∞(Rn)×Lr(Sn-1)=
(1)

并设Ω满足条件Ω(x,λz)=Ω(x,z),∀x,z∈Rn,∀λ>0,与消失条件:
∀x∈Rn。
(2)
带变量核的奇异积分算子TΩ定义如下:
(3)
下面,先给出一些本文中所用的定义与记号。
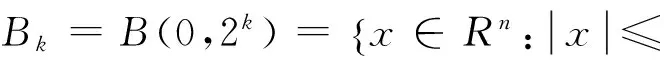

定义1[9]设α∈R,0 (5) 定义2[10]设1 (6) 则称ω(x)是一个Ap权,记作ω(x)∈Ap。 定义3[9]设s>1,若存在一个常数C>0,使得对每个球B∈Rn,有: (7) 则称ω(x)满足反向Hölder不等式,记作ω(x)∈RHs。 定义4[9]设1≤q,p,α≤∞,ω(x)是一个权函数,定义 (8) 本文的主要结果如下 ‖TΩ(f)‖qω,p,α≤C‖f‖qω,p,α。 为证明定理,需要以下引理 引理1[9]设ω∈RHs,且s>1,那么存在常数C>0,使得: 对于球体B的任意可测子集E都成立。 引理2的证明具体可参见文献[9]。 ‖TΩ(f)χB‖qω≤‖TΩ(f1)χB‖qω+ ‖TΩ(f2)χB‖qω=I1+I2。 由引理2可得 I1=‖TΩ(f1)χB‖qω≤C‖f1‖qω=C‖f1χ2B‖qω。 (10) 以下估计I2,由Hölder不等式 当x∈B,y∈2j+1B2jB时,有 因此 故有 (11) 根据引理1知,存在一个常数s>1,使得: ‖TΩ(f)‖qω,p,α≤C‖f‖qω,p,α。 至此,定理1证毕。 [1]A.P.CalderonandA.Zygmund,OnaproblemofMihlimTrans[J].Amer,Math.Soc.1995,78:209-224. [2]Calderon,AandZygmund,A.,Onsingularintegralwithvariablekernels[J].Appl.Anal.,1978,7:221-238. [3]邵旭馗,王素萍.齐次Herz空间上的奇变量核Marcinkiewicz积分算子[J].陇东学院学报(自然科学版),2010(2):4-7. [4]J.Chen,Y.DingandD.Fan.AclassofintegraloperatorswithvariablekernelsonHardyspaces[J].ChineseAnnalsofMath.(A),2002,23:289-296. [5]DINGYong,LUShan-zhen,SHAOShuang-lin.Integraloperatorswithvariablekernelsonweakhardyspaces[J].MathAnalAppl,2006,317(1):127-135. [6]闫彦宗,邵旭馗,王素萍.变量核的Marcinkiewicz高阶交换子在Hardy空间的有界性[J].山东大学学报(理学版),2013,48(2):67-71. [7]DINGYong,LINQin-cheng,SHAOShuang-lin.OntheMarcinkiewiczintegralwithvariablekernels[J].IndianaUnivMathJ,2004,53(3):805. [8]ZHANG P,LAN S H.Weak type estimates for commutators of the Marcinkiewicz integral on Herz-type spaces [J].AdvinMath,2007,36(1):108-114. [9]LU S Z,YANG D C.The weighted Herz-type Hardy spaces and its applications[J].ScienceinChina,1995,6A:662-673. 【责任编辑 朱世广】 Boundedness of the Singular integral Operators with variable kernels on Weighted (Lq,Lp)α(Rn) spaces SHAO Xu-kui,WANG Su-ping (SchoolofMathematicsandStatistics,LongDongUniversity,Qingyang745000,Gansu) The boundness of the Singular integral operators with variable kernelsTΩisdiscussed.ByusingthepropertiesofkernelfunctionΩ,theboundnessofTΩonweighted(Lq,Lp)α(Rn) space is proved. Singular integral operators; weighted (Lq,Lp)α(Rn) space; Variable kernel 2016-10-10 国家自然科学基金项目《变指数空间上Littlewood-Paley算子及相关算子的研究与应用》(11561062);甘肃省高等学校科研项目《一类变量核奇异积分算子及其交换子的有界性研究》(2015A-147) 邵旭馗(1979—),男,甘肃天水人,副教授,硕士,主要从事调和分析及其在偏微分方程中的应用研究。 1674-1730(2017)03-0001-03 O A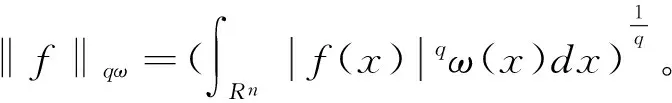


2 定理的证明