一类具有信息孤岛的时滞信息传播模型

王有刚， 闫洋龙， 齐子健， 虞成跃， 张子振

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

一类具有信息孤岛的时滞信息传播模型

王有刚， 闫洋龙， 齐子健， 虞成跃， 张子振

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

针对负面信息传播的危害性，并考虑到信息传播的非瞬时性，提出一类具有信息孤岛和传播延迟的信息传播模型。以信息传播延迟为分支参数，进一步研究了模型的Hopf分支的存在性。然后通过分析相应特征方程根的分布，得到信息传播模型的局部稳定和产生局部Hopf分支的充分性条件。最后，给出一个数值模拟例子，验证了所得理论分析结果的正确性。研究表明，尽量延迟Hopf分支的发生，可以有效控制负面信息在社会上的传播，减少社会危害性。所得结果为有效控制负面信息传播提供了理论参考依据。

信息传播；传播模型；时滞；稳定性；Hopf分支

信息化社会里，信息传播在现实世界中起着越来越重要的作用。然而信息传播是把双刃剑，对于社会的稳定和发展有着积极和消极两方面的影响，如何对信息传播的过程进行有效控制，以减少和削弱负面信息的危害，发挥信息传播的积极作用成为当前研究的一个热点问题。利用数学建模方法模拟信息传播过程已经成为信息科学领域中的一个重要课题[1]。基于SIS模型，文献[2]提出了一类级联信息模型，并研究了信息如何通过博客传播。文献[3]研究了一类信息在人际网络上传播的模型，并对所得理论结果进行了计算机模拟。文献[4]则提出了一个基于在线社交网络的信息传播模型，利用复杂网络和传染病动力学理论，模拟了在线社交网络中的信息传播过程，为深刻理解在线社交网络中的传播行为提供了理论基础。

但是，上述这些信息传播模型，并未考虑到信息传播过程中，对信息的传播控制问题。众所周知，信息可以分为多种类型。对于诸如先进文化和有用知识之类的有用信息，应该对其进行广泛的深度开发，为决策者提供有效的决策依据。然而，对于谣言之类的负面信息，应该采取积极的控制措施对其进行隔离。另外，目前所研究的信息传播模型，都假设信息从信源到信宿的传播是瞬时的。这显然与实际信息传播过程不相吻合，因为信息的传播肯定是需要一个时间周期的。即，目前所研究的信息传播模型忽略了信息从信源到信宿的传播周期。延迟因素对动力学模型的稳定性具有非常重要的影响，在一定条件下可能会引起Hopf分支的发生。关于具有延迟的动力系统Hopf分支的研究工作，已经取得了一定的成果[5-9]。文献[5-6]分别研究了一类具有延迟的经济增长模型的Hopf分支的存在性；文献[7-8]分别研究了一类具有消极负反馈延迟的捕食系统模型的Hopf分支的存在性，并对Hopf分支的性质进行了研究；文献[9]则研究了一类具有延迟的商业周期模型的Hopf分支问题；以上文献均以模型中的延迟为分支参数，对Hopf分支的存在性进行了分析，得到了一些有益的理论结果。

受以上研究工作的启发，并考虑到信息传播过程中负面信息的危害性，以及信息传播过程中的传播延迟，本文首先构建一个具有信息孤岛和信息传播延迟的信息传播模型，然后以信息传播延迟为分支参数，分析信息传播延迟对模型稳定性的影响。最后，给出一个仿真示例，对理论分析结果的正确性进行验证。

1 模型描述

文献[10]基于如下假设，提出了下列具有信息孤岛的信息传播模型（1）：

a）模型中具有三类个体：无知者x，即对信息一无所知的个体；传播者y，即获知信息并对信息继续散播的个体；被隔离者z，即为了防止负面信息继续传播而被隔离的个体。

b）模型中存在出生事件和死亡事件，并且所有的新出生人口均为无知者。

d）信息传播具有不同的阶段，因此，隔离项在信息传播不同的阶段也应该具有不同的形式。在模型中采取的信息隔离函数为

e）模型中个体与个体之间，采取相同的形式进行信息传播。即忽略个体的差异性。

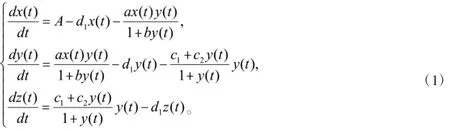
其中，x(t)、y(t)和z(t)分别表示无知者、传播者和被隔离者在时刻t的数量。A表示人口出生率，d1表示人口自然死亡率。为信息传播函数，用来描述信息传播率。为信息隔离函数，用来描述信息隔离程度。

考虑到信源到信宿的传播周期，本文在模型（1）中引入信息传播延迟，得到下列具有信息传播延迟的信息传播模型：

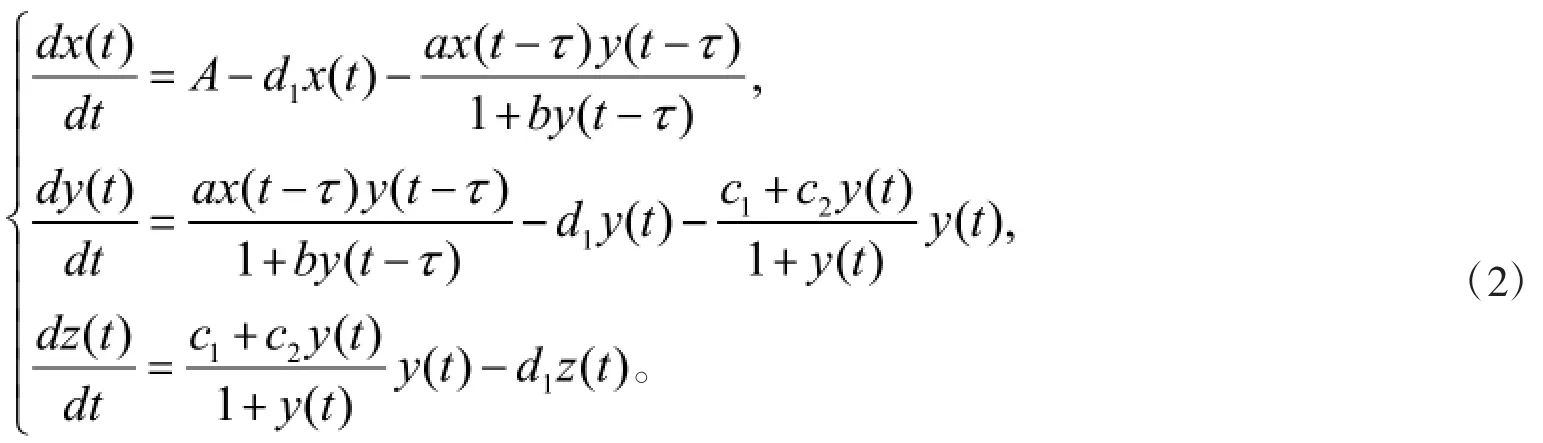
2 正平衡点的存在性

鉴于模型（2）的物理含义，本文只考虑模型（2）的正平衡点模型（2）的正平衡点可以通过求解下列方程组得到：

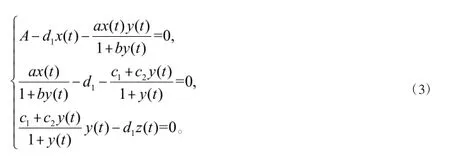
根据方程组 (3)中的第二个方程和第三个方程，可以分别得到把x*，z*的表达式代入方程组（3）中的第一个方程得到关于y*的一元二次方程：

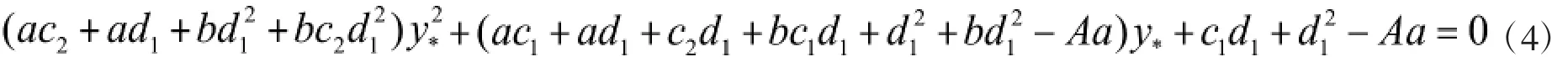
为了方便起见，令

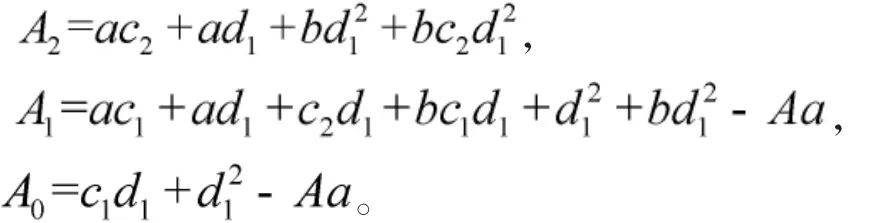
方程（4）可以变为下列形式：

根据文献[11]对方程（5）根的讨论结果，可以得到下列结论。

a）如果A2=0且A0/A1＜0，方程（5）存在唯一正根y*=-A0/A1；

b）如果△=A21-4A2A0＞0，那么当A1/A2＜0且A0/A2＞0时，方程（5）存在两个正根和；当A0/A2＜0且A2＞0（A2＜0），方程（5）存在唯一正根y+*（y-*）。当A0=0且A1/A2＜0时，方程（5）存在唯一正根y*=-A1/A2；

c）如果△=A21-4A2A0=0且A1/A2＜0时，方程（5）存在唯一正根y*=-A1/（2A2）。

经过以上分析可知，如果模型（2）中的参数满足以上a）-b）中的任何一个条件，则模型（2）至少存在一个正平衡点。

3 信息传播延迟对模型的影响分析

作平移变换u1(t)=x(t)-x*，u2(t)=y(t)-y*，u3(t)=z(t)-z*，仍然记u1(t)，u2(t)，u3(t)为x(t)，y(t)和z(t)。

模型（2）在正平衡点E(x*，y*，z*)处的线性化系统为：

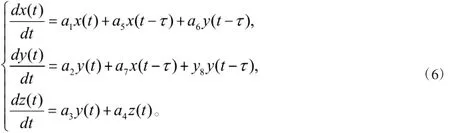
其中，

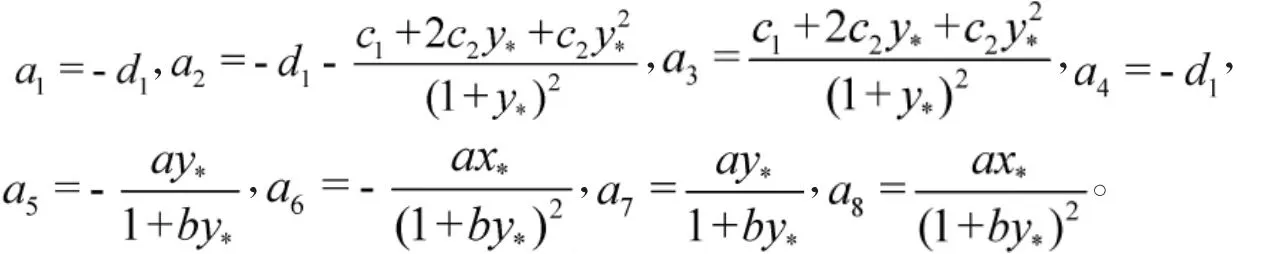
得到系统（6）的特征方程：

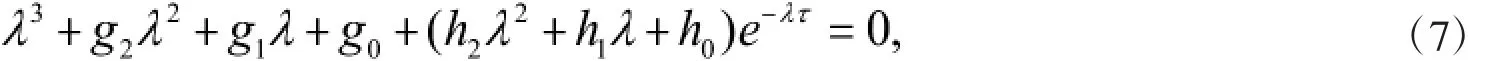
其中，

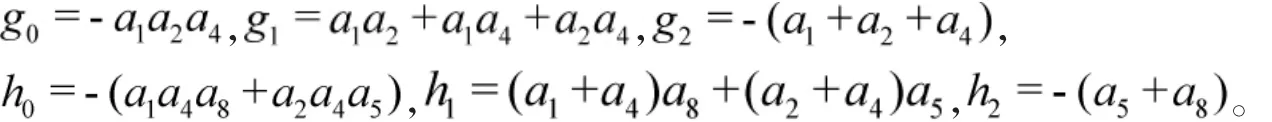
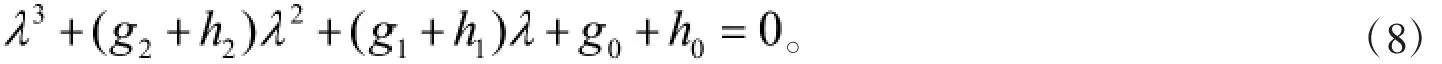
进而，得到

令w2=，方程（10）变为

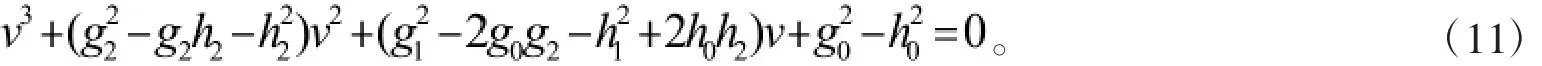
为了给出本文主要结果，我们给出如假设：（H2）∶方程(11)至少存在有一个正根。如果条件（H2）成立，那么方程（11）存在一个正根0使得方程（10）存在一对纯虚根所以，有

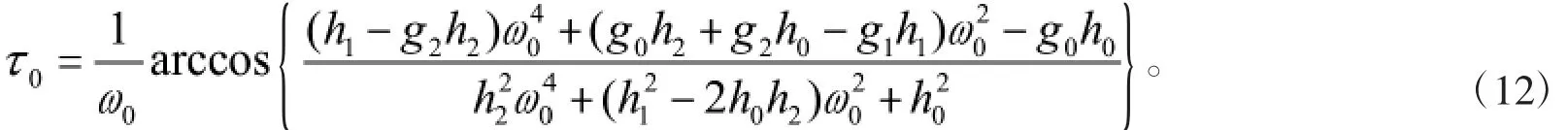
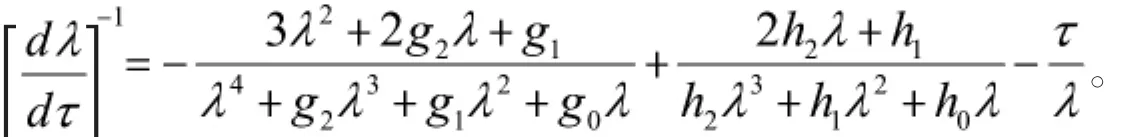
因此，

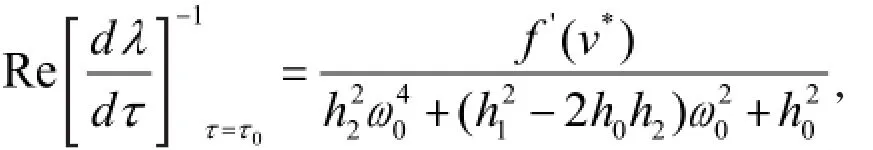
定理1 对于模型（2），如果（H1）-（H3）成立，则当∈[0，）时，模型（2）的正平衡点E*(x*，y*，z*)是局部渐近稳定的；当=时，模型（2）在正平衡点 E(x*，y*，v*)处产生 Hopf分支，其中

4 仿真示例

为了验证本文理论分析结果的正确性，我们给出一个仿真示例。需要强调的是本文只是对具有信息孤岛和传播延迟的信息传播模型动力学性质进行了理论分析，希望可以对现实生活中有害信息的传播控制提供理论指导依据。因此，所用到仿真示例系统参数并不是来自于现实生活中的实际实验。选取文献[10]中的部分系统参数值，并考虑到系统（2）产生Hopf分支的条件，我们对系统（2）选取下列一组参数值：A=10，d1=0.1，a=0.2，b=0.01，c1=1，c2=0.5。得到模型(2)的如下示例系统：

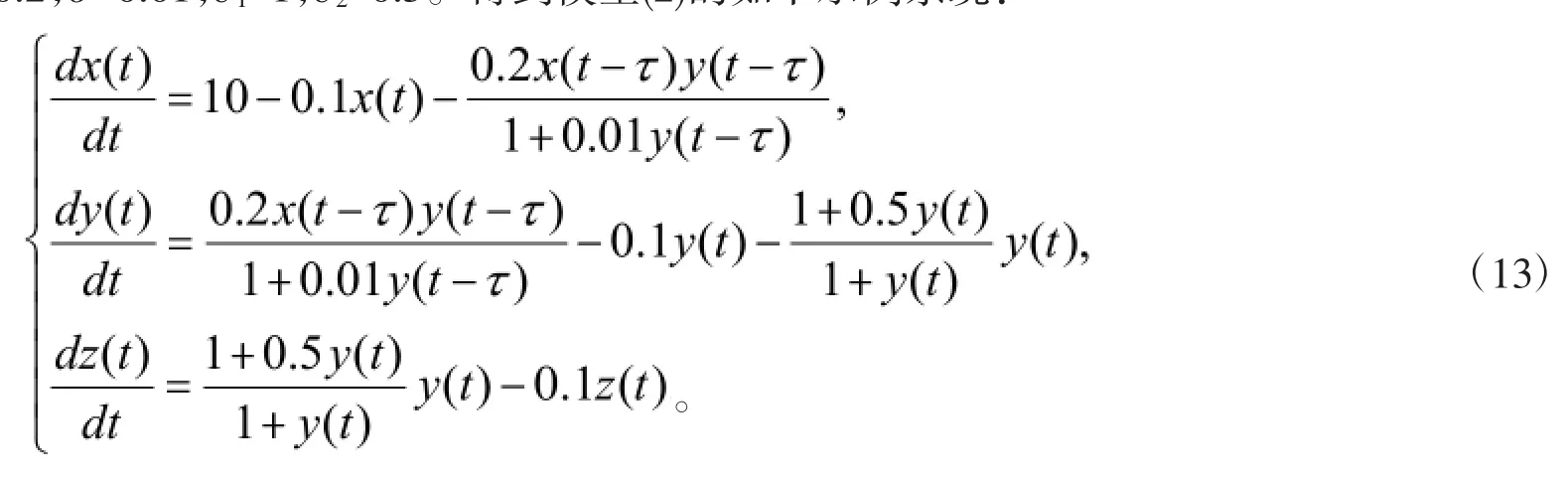
经过计算可以得知，此时方程（5）变为

显然，对于方程（13）有△=3.8633＞0，A2=0.1202＞0，A0/A2=-15.7238＜0。因此，根据第3部分的分析可知，方程（14）存在唯一正根。利用Matlab软件计算可以得到=15.3263。进而得到系统(13)的唯一正平衡E（*3.6364，15.3263，81.3252），并计算得到a1=-0.1，a2=-0.6019，a3=0.5019，a4=-0.1，a5=-2.6579，a6=-0.5468，a7=2.6579，a8=0.5468，g0=0.0060，g1=0.1304，g2=0.8019，h0=0.1545，h1=1.7562，h2=2.1111。因此，可以验证条件（H1）成立。进而，方程（11）变为：

利用 Matlab软件计算可以得到方程（15） 的唯一正根0=5.9170。从而得到 ω0=2.4325，，即，条件（H2）与（H3）成立。根据表达式（12）计算得到传播延迟时滞临界点0= 0.7014。当我们取=0.6350∈[0，0.7014）时，系统(12)是局部渐近稳定的，仿真效果如图1所示。而当我们取=0.7325＞0.7014时，系统（12）失去稳定性，在正平衡点处产生Hopf分支并分支处一簇分支周期解。仿真效果如图2所示。

图1 当=0.6350＜0.7014时的相图轨迹

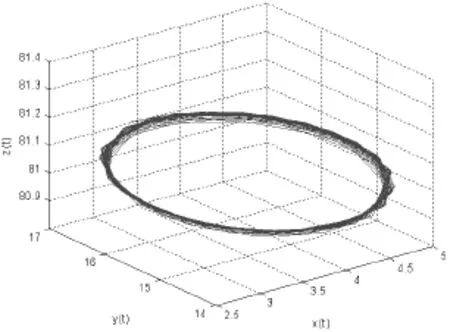
图2 当=0.7325＜=0.7014时的相图轨迹

5 结论

本文研究了一类具有信息孤岛的时滞信息传播模型。通过分析模型相应特征方程根的分布，给出了模型局部渐近稳定和局部Hopf分支存在的充分性条件。研究表明，当信息传播延迟所引起的时滞取值小于特定临界值（）时，模型局部渐近稳定。此时，对于信息的传播控制，可以采取合理的有效控制措施。而一旦时滞的取值超过临界值（），模型将失去稳定性并产生Hopf分支。此时，将不利于信息传播的控制。由此可以发现，信息传播延迟对信息传播模型的动力学性质具有重要的影响。最后，利用数值模拟对理论分析结果的有效性进行了验证。

另外，需要指出的是，我们只是从理论上分析了信息传播延迟所引起的时滞对模型（2）的影响，并利用数值模拟对所得结果进行了验证，并未将其应用到实际的信息传播过程中。我们希望本文所得结果能够对实际的信息传播过程进行适当控制提供理论指导依据。为了衡量模型在实际的信息传播过程中的应用效果，我们需要收集大量的相关数据，并通过统计分析相关数据，不断调整模型中的参数。如果实际的信息传播过程能和本文所研究的模型动力学性质相吻合，则说明模型在实际的信息传播过程中是有效的。否则，我们将需要修改完善本文所研究的模型。这也是我们下一步需要解决的研究问题。

参考文献：

[1]MORENO Y，NEKOVEE M，PACHECO A F.Dynamics of rumor spreading in complex networks[J].Physical Review E.Statistical，Nonlinear，and Soft Matter Physics，2004，69（6）：1-8.

[2]LESKOVEC J，McGlohon，FALOUTSOS C，et al.Patterns of cascading behavior in large blog ggraphs[C]//proceedings of the 7th SIAM International conference on Data Mining，2007：551-556.

[3]孙庆川，山石，兰田田.一个新的信息传播模型及其模拟[J].图书情报工作，2010，54（6）：52-56.

[4]张彦超，刘云，张海峰，等.基于在线社交网络的信息模型[J].物理学报，2011，60（5）：60-66.

[5]BIANCA C，FERRARA M，GUERRINI L.The cai model with time delay：Existence of periodic solutions and asymptotic analysis[J].Applied Mathematics and Information and Sciences，2013，7（1）：21-27.

[6]BIANCA C，FERRARA M，GUERRINI L.Hopf Bifurcations in a Delayed-energy-based Model of Capital Accumulation[J].Applied Mathematics&Information Sciences，2013，7（1）：139-143.

[7]KAR T K，GHORAI A.Dynamica behavior of a delayed predator-prey model with harvesting[J].Applied Mathematics and Computation，2011，217（22）：9085-9104.

[8]ZHANG J F.Bifurcation analysis of a modified holling-tanner predator-prey model with time delay[J].Applied Mathematical Modelling.2012，36（3）：1219-1231.

[9]于晋臣，彭名书，张彩艳.一类具有时滞的商业周期模型的Hopf分支[J].北京交通大学学报，2013，37（3）：139-142.

[10]ZHAO X X，WANG J Z.Dynamics of an information spreading model with isolation[J].Abstract and Applied Analysis，2014（5）：6.

[11]LI C D，HU W F，HUANG T W.Stability and bifurcation analysis of a modified epidemic model for computer viruses[J].Mathematical Problems in Engineering，2014，（1）：14.

[12]HASSARD B D，KAZARINOFF N D，WAN Y H.Theory and applications of hopf bifurcation[M].Cambridge University Press，Cambridge，1981.

An Information Spreading Model with Isolation and Delay

WANG Youɡɑnɡ，YAN Yɑnɡlonɡ，QI Zijiɑn，YU Chenɡyue，ZHANG Zizhen

（School of Management Science and Engineering，Anhui University of Finance and Economics，Bengbu Anhui 233030，China）

A delayed model for information spreading with isolation is investigated in this paper.Existence of Hopf bifurcation of the model is studied by regarding the time delay，using information spreading as a bifurcation parameter.The sufficient conditions for the local stability and existence of local Hopf bifurcation of the model are obtained by analyzing distribution of roots of the associated characteristic equation.Finally，a numerical example is presented to testify the effects of theoretical results，which provide theoretical reference to control information spreading.Studies have shown that delaying the occurrence of Hopf bifurcation can effectively control the spread of negative information on the society and to reduce harmfulness on the society.The results provide theoretical reference basis to effectively control the spread of the negative information.

Information Spreading；Spreading Model；Delay；Stability；Hopf Bifurcation

D175

A

1009-8666（2017）04-0047-06

10.16069/j.cnki.51-1610/g4.2017.04.010

［责任编辑、校对：王兴全］

2017-04-10

安徽省2016年自然科学基金资助项目“具有分级感染率的时滞网络病毒传播模型动力学性质研究”（1608085QF151）

王有刚(1967—)，男，山东烟台人。安徽财经大学副教授，硕士，研究方向：信息安全；闫洋龙（1997—），男，安徽阜阳人。安徽财经大学本科生。