Addition-Min合成模糊关系方程的解集

屈小兵， 孙 峰

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

Addition-Min合成模糊关系方程的解集

屈小兵， 孙 峰

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

文章主要讨论了Addition-min合成模糊关系方程的解集的性质，得到了方程存在最大解和最小解的一些条件，给出了极大解和极小解的结构。

Addition-min合成模糊关系方程；解集；极大解；极小解

0 引言

自1976年E.Sanchez[1]首先提出并研究了完备Brouwerian格上的max-min合成模糊关系方程后，很多学者对完备Brouwerian格上的不同合成算子的模糊关系方程进行了深入的研究[2-5]。现在模糊关系方程已被广泛应用于模糊逻辑推理和图像处理等很多领域[6-8]。最近，Li和Yang[9-10]等针对实验室点对点网络优化管理问题进行了研究，建立了一个以Addition-Min合成模糊关系不等式组为约束条件的优化模型，并通过研究Addition-Min合成模糊关系不等式的解集的性质得到了求解该模型最优解的一种方法。此后，Yang[11]等改进了这个模型，并得到了求解模型最优解的一种方法。从他们对模型最优解的研究可知最优解与模糊关系不等式的极小解紧密相关，而不等式的极小解又与对应的Addition-Min合成模糊关系方程的解有直接联系。所以为能更好地求解模型，本文将主要研究Addition-Min合成模糊关系方程的解集的性质。

设实验室有n个用户终端，每一个用户可以从其他任一终端下载数据，同时也对其他终端共享自己的数据，这是一个点对点的实验室网络系统。设A1，A2，…An为n个用户终端，aij表示终端Ai与Aj之间的带宽，xj表示第j个终端发送信息的质量水平。因为带宽有一定的限制，所以终端Ai从Aj下载数据的实际速度为，如果Ai从其他终端下载数据的最低速度需求为b（ibi＞0），那么包含n个终端的实验室点对点网络系统可以表示为：

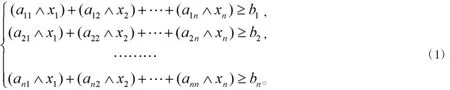
其中aii=0，i=1，2，……n。一般的Addition-Min合成模糊关系不等式如下：

为计算方便，规定aij，xj∈[0.1]，bi＞0，i∈I={1，2，…，m}，j∈J={1，2…，n}.系统(2)也可以记为Ax≥b，其中

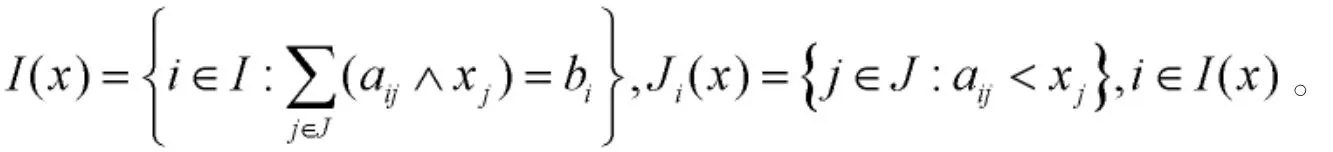
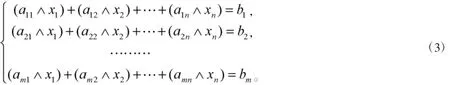
或者A◦x=b，其中“◦”表示Addition-Min合成。记方程(3)的解集为和X*分别表示方程(3)的极大解集和极小解集。

1 预备知识

为讨论方便，本节先给出一些预备知识。

证明：设a，b，c∈[0，1]，下面分两种情况讨论：

1）若b+c≤a，则b≤a，c≤a，从而

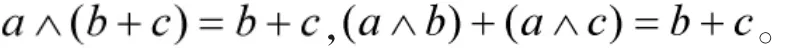
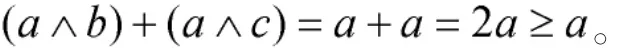
另外，如果a≥b+c，则由前面的证明可知

引理1.1说明Addition和Min这对算子不满足分配律，所以Addition-Min合成模糊关系方程与Max-Min等合成模糊关系方程的解集性质具有较大差异。

2 主要结论

下面主要讨论系统(3)的一种特殊情况，即|I|=1，方程为

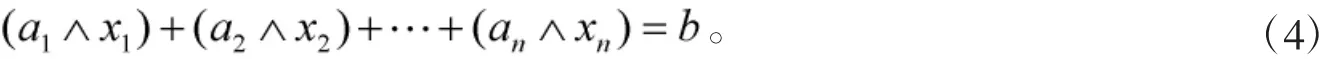
证明：结论显然成立。

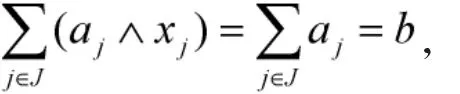
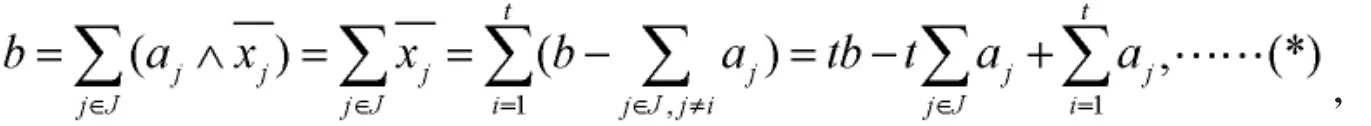
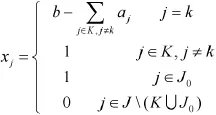
则x是方程(4)的一个极大解。

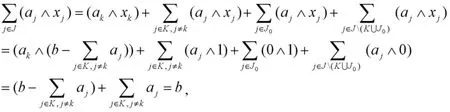
所以x∈X。

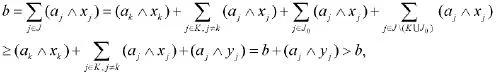
矛盾。所以∀i∈J，yj=xj.因此y=x，即x是一个极大解。

注2.2方程的极小解一般有无穷多个，如在例2.1中，

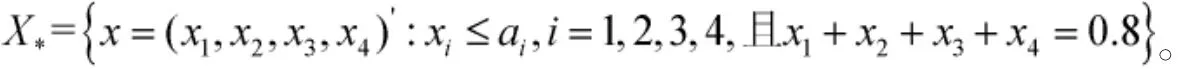
显然，｜X*｜=∞。另外，方程的极小解可能也是极大解，如在例2.1中，（0.8,0,0,0）′，（0.7,0.1,0,0）′∈X*。由此可知，Addition-min合成模糊关系方程的解集刻画比其他合成模糊关系方程要复杂。对一般的方程A◦x=b，有解的时候不一定有最大解或者最小解，所以有解的判定就比较困难。

例2.2 在方程组A◦x=b中，其中

[1]SANCHEZ E.Resolution of composite fuzzy relation equations[J].Information and Control，1976，30：38-48.

[2]DI NOLA A，SESSA S，PEDRYCZ W，ect.Fuzzy relational equations and their applications to knowledge engineering[M].Kluwer Academic Publishers，Dordrecht，Boston/London，1989.

[3]王学平.完备格上模糊关系方程的研究进展[J].四川师范大学学报(自然科学版)，2009，32（3）：365-376.

[4]MOLAI A A.Resolution of a system of the max-product fuzzy rrelation equations using L U-factorization[J].Information Sciences，2013，234：86-96.

[5]LOETAMONPHONG J，FANG S G.Optimization of fuzzy relational equations with max-product composition[J].Fuzzy Sets and Systems，2001，118：509-517.

[6]NOBUHARA H，BEDE B，HIROTA K.On various eigen fuzzy sets and their application to image reconstruction[J].Information Sciences，2006，176：2988-3010.

[7]DI NOLA A，RUSSO C.Lukasiewicz transform and its application to compression and reconstruction of digital images[J].Information Sciences，2007，177：1 481-1 498.

[8]杨晓鹏，杨晓斌.模糊关系方程在实验室点对点网络系统中的应用[J].辽宁工程技术大学学报（自然科学版），2016，35（1）：81-84.

[9]LI J X，YANG S J.Fuzzy relation equalities about the data transmission mechanism in bittorrent-like peer-to-peer file sharing systems[J].in Proc.9th Int.Conf.Fuzzy Syst.Knowl.Discovery，2012：452-456.

[10]YANG S J.An Algorithm for minimizing a linear objective function subject to the fuzzy relation inequalities with addition-min composition[J].Fuzzy Sets and Systems，2014，255：41-51.

[11]YANG X P，ZHOU X G，CAO B Y.Min-aax programming problem subject to addition-min fuzzy relation inequalities[J].IEEE Transactions on Fuzzy Systems，2016，24（1）：111-119.

Solution Sets of Fuzzy Relation Equations with Addition-Min Composition QU Xiɑobinɡ，SUN Fenɡ

（School of Mathematics and Information Science，Leshan Normal University，Leshan Sichuan 614000，China）

In this paper，some properties of solution sets of fuzzy relation equations with Addition-Min Composition are discussed，and some conditions for the existence of maximal solution and minimal solution are obtained.Furthermore，the structure of maximal solutions and minimal solutions are given.

Fuzzy Relation Equations with Addition-Min Composition；Solution Set；Maximal Solution；Minimal Solution

O159

A

1009-8666（2017）04-0006-05

10.16069/j.cnki.51-1610/g4.2017.04.002

［责任编辑、校对：李书华］

2017-04-10

四川省科技厅应用基础项目“完备格上Fuzzy关系方程的求解及其应用”（2016JY0235），“基于多目标和双层规划的个性化推荐系统模型和算法研究”（2017JY0208）；四川省教育厅项目“分数阶微积分理论及其应用研究”（16TD0029），“半线性空间及其应用研究”（16ZA0303）；乐山师范学院科研项目“半线性空间上模糊关系方程的求解”（Z1411）

屈小兵（1974—），男，湖南永州人。乐山师范学院副教授，博士，研究方向：格上方程；孙峰（1985—），男，四川西昌人。乐山师范学院副教授，硕士，研究方向：模糊算子。