梯度负泊松比蜂窝材料的冲击动力学性能分析*

尹冠生姚兆楠

（1.长安大学理学院，西安 710054）（2.葛洲坝勘测设计研究院有限公司，武汉 430000）

梯度负泊松比蜂窝材料的冲击动力学性能分析*

尹冠生1姚兆楠2†

（1.长安大学理学院，西安 710054）（2.葛洲坝勘测设计研究院有限公司，武汉 430000）

借助非线性有限元程序LS-DYNA，基于功能梯度材料的概念，改变蜂窝胞壁厚度，建立了具有密度梯度的内凹六边形负泊松比蜂窝材料模型.分析对比了均匀负泊松比蜂窝材料和梯度负泊松比蜂窝材料在不同面内冲击速度下的变形模式、动态响应和能量吸收特性.研究表明，梯度负泊松比蜂窝材料的动态响应和能量吸收能力受梯度、胞元内凹角度和冲击速度的影响.如果能适当选取各项参数，就可使材料在降低初始应力峰值的同时保持良好的能量吸收能力.因此，具有密度梯度的负泊松比蜂窝材料在结构防护方面具有良好的应用前景.

密度梯度，负泊松比蜂窝材料，功能梯度材料，动态冲击，力学性能

引言

由于质量轻、抗冲击和能量吸收性能良好，蜂窝（honeycombs）和泡沫（foams）等多孔材料被广泛应用在国防、化工、能源、微电子、交通、生物医学、航空航天［1］等各个领域中.随着对负泊松比材料研究的深入，具有负泊松比效应的蜂窝材料也相应出现.负泊松比（auxetic）材料［2］在受到单轴拉伸时会发生侧向膨胀，这种独特的“拉胀”行为使它表现出更强的力学和物理特性，包括剪切模量、断裂韧性、热冲击强度、压痕阻力等.1982年，Ashby［3］首先提出，由细胞结构组成的材料能够通过变形产生负泊松比效应，这一成果使负泊松比材料的研究与应用得到发展.1987年，Lakes［4］通过对普通聚氨酯泡沫进行三维压缩、加热、冷却和松弛处理，首次得到了内凹结构单元，成功制备出具有泊松比效应的聚氨酯泡沫；卢子兴等［5］建立了具有负泊松比效应的二维多孔材料力学模型，研究了单元细胞的几何尺寸对材料剪切模量和刚度的影响；卢文浩等［6］对六边形蜂窝材料单个胞体和多个胞体在动态冲击下的变形情况和能量吸收能力进行了研究；张新春等［7］数值模拟了具有内凹六边形单元的负泊松比蜂窝材料的面内冲击行为，分析了内凹角度对结构动态响应和能量吸收性能的影响.

一般来说，多孔材料的动态响应曲线会存在一个远大于平台应力（plateau stress）的初始应力峰值，这对于其实际工程应用十分不利.因此，初始应力峰值的控制和能量吸收性能的增强控制成为蜂窝材料设计中的关键问题.功能梯度材料［8］（FGM）在受到面内冲击作用时，其动态响应和变形模式会随着梯度的变化而在局部发生变化，这样可以减少局部应力集中，确保结构的整体性和可靠性.因此，与传统多孔材料相比，功能梯度多孔材料在抗冲击、能量吸收等方面具有一定的优越性.V.P.W Shim等［9］探讨了正方形和六边形排布的圆环蜂窝在面内动态荷载作用下的变形机制和力学性能；L.L.Hu［10］、D.Karagiozova［11］等研究了圆环蜂窝材料在动态冲击下的变形机制，并取得了可观的成果.刘颖等［12］提出了一种分层递变梯度多孔圆环蜂窝模型，发现通过适当选取不同冲击速度下的梯度系数和圆环排布方式，能够有效调整蜂窝材料的吸能特性.张新春等［13］根据功能梯度材料的概念，构造了具有密度梯度的蜂窝材料模型，根据蜂窝单元细胞的几何尺寸来调整蜂窝材料的密度梯度分布，从而控制材料的能量吸收能力.

本文研究了具有密度梯度的负泊松比蜂窝材料在不同冲击速度下的变形模式、动态响应和能量吸收特性，并与相应的均匀负泊松比蜂窝进行对比，分析梯度负泊松比蜂窝材料在冲击荷载作用下的力学性能.

1 计算模型

1.1 单个胞元的有限元分析

从整体蜂窝材料中取出一个胞单元，分析胞单元表现出来的力学行为.本文以具有内凹六边形单元的负泊松比蜂窝材料为研究对象，其胞元结构如图1所示.取α＝1，边长h＝l＝2.7mm，壁厚t＝0.27mm，斜肋与竖向的夹角θ＝25°.蜂窝试件的面内冲击载荷通过刚性板施加，冲击模型如图2所示，刚性板以速度v＝10 m／s沿y方向从上至下进行冲击.

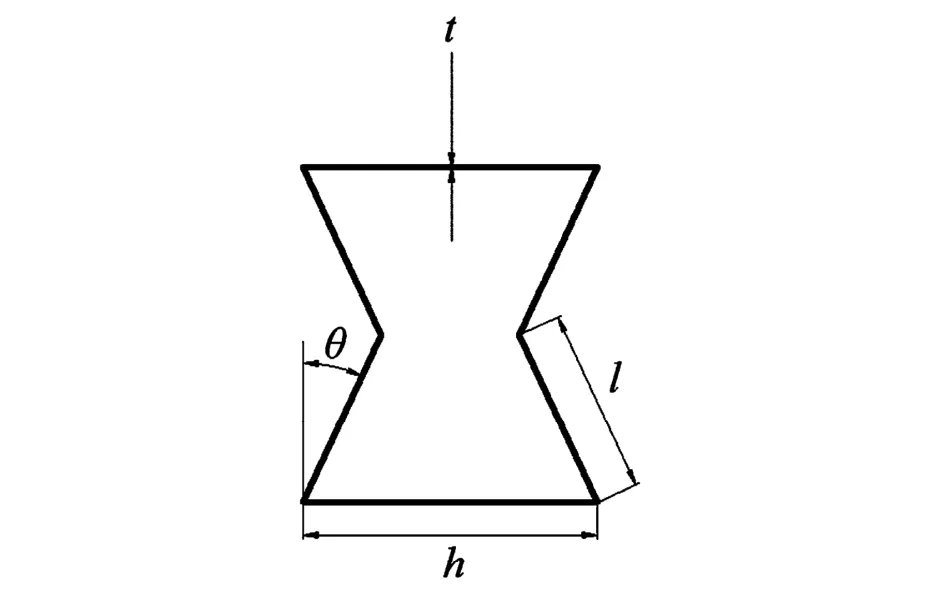
图1 负泊松比蜂窝的胞元结构Fig.1 Cell configuration of auxetic honeycombs

图2 蜂窝试件的面内冲击示意图Fig.2 Diagrammatic sketch of honeycombs under in-plane impact

本文采用ANSYS／LS-DYNA对负泊松比蜂窝材料的冲击力学行为进行数值模拟计算.蜂窝的基体材料为铝合金，采用理想弹塑性模型，选用壳单元SHELL163，沿厚度方向定义5个积分点；刚性板采用刚体来定义，选用SOLID64单元，具体材料参数见表1.将冲击过程中刚性板与蜂窝之间的接触定义为单面自动接触，即采用*CONTACT＿AUTOMATIC＿SINGLE＿SURFACE接触算法，不考虑摩擦作用.蜂窝试件底部采用全约束，左右两边无约束.为防止蜂窝试件在面外发生体积膨胀，所有节点的z向位移都被约束，z向的厚度c＝1mm.

表1 材料参数Table 1 Material parameters

经过ANSYS／LS-DYNA程序的计算，得到图3所示的分析后的变形图.单个胞体的应力应变关系曲线如图4所示，可以发现应力在初始时急剧增长并达到第一个峰值，然后剧烈下降，表明胞元材料在冲击中经过弹性阶段进入塑性阶段，且在胞元上产生了塑性铰，如图3（b）中所示.当应力再次急剧增长时，此时正是胞元的上下部分即将被完全压实的时候.

图3 单个胞元面内变形模式Fig.3 In-plane deformation modes of single cell

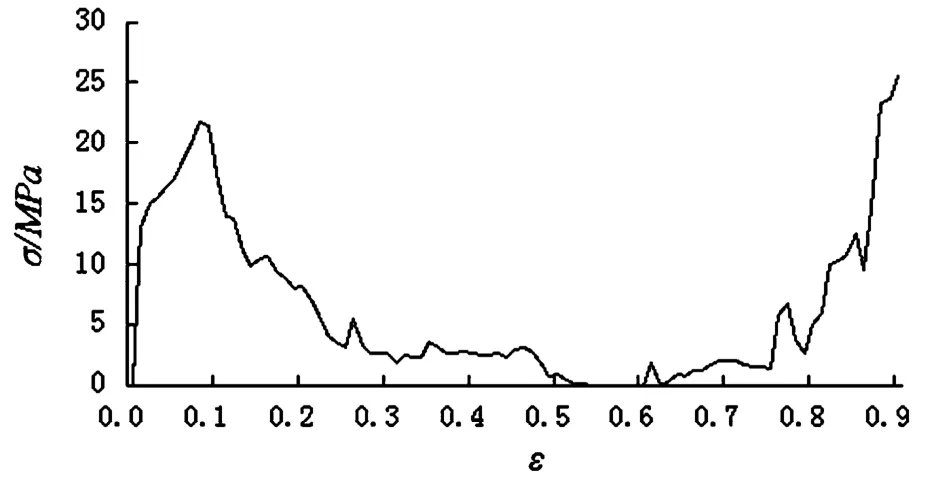
图4 单个胞元应力应变曲线Fig.4 Nominal stress-strain curves of single cell

1.2 蜂窝结构有限元模型

蜂窝结构试件的面内冲击载荷同样通过刚性板施加，冲击模型如图2所示，刚性板以三种初始速度（50、100和120m／s）沿y方向从上至下进行冲击.均匀负泊松比蜂窝试件的尺寸及相对密度见表2，试件分别由胞元边长和胞壁厚度（取 t＝0.27mm）相同、内凹角度不同（θ＝10°、15°、20°和25°）的蜂窝单元填充（如图5所示）.具有密度梯度的负泊松比蜂窝试件的尺寸及密度参数见表3，试件分别由具有相同胞元边长、不同内凹角度（分别取为θ＝10°、15°、20°和25°）的蜂窝单元填充.具有密度梯度的负泊松比蜂窝材料在压缩方向被分为五部分，每部分内蜂窝单元的胞壁厚度一样，相邻蜂窝胞壁厚度的改变量Δt＝±0.02mm.Δt＞0时是正梯度蜂窝，试件沿y轴正向密度增加；Δt＜0时是负梯度蜂窝，试件沿y轴正向密度减小.梯度负泊松比蜂窝试件的有限元模型如图6及图7所示（此处给出θ＝10°的模型作为说明），其中图6所示为正梯度蜂窝，胞壁厚度t从上向下依次为0.23mm、0.25mm、0.27mm、0.29mm、0.31mm；图7所示为负梯度蜂窝，胞壁厚度t从上向下依次为0.31mm、0.29mm、0.27mm、0.25mm、0.23mm.

表2 均匀负泊松比蜂窝试件的尺寸及相对密度Table 2 Size and relative density for homogeneous auxetic honeycombs

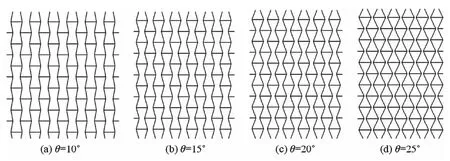
图5 具有不同凹角的均匀负泊松比蜂窝试件示意图Fig.5 Diagrammatic sketch of homogeneous auxetic honeycombs with various re-entrant angles

表3 梯度负泊松比蜂窝试件的尺寸及密度参数Table 3 Size and relative density for graded auxetic honeycombs

本文采用ANSYS／LS-DYNA对负泊松比蜂窝材料的冲击力学行为进行数值模拟计算.蜂窝的基体材料为铝合金，采用理想弹塑性模型，选用壳单元SHELL163，沿厚度方向定义5个积分点；刚性板采用刚体来定义，选用SOLID64单元，具体材料参数见表1.将冲击过程中刚性板与蜂窝、蜂窝内部之间的接触均定义为单面自动接触，即采用* CONTACT＿AUTOMATIC＿SINGLE＿SURFACE接触算法，不考虑摩擦作用.蜂窝试件底部采用全约束，左右两边无约束.为防止蜂窝试件在面外发生体积膨胀，所有节点的z向位移都被约束，z向的厚度c＝1mm.

图6 正梯度负泊松比蜂窝试件的有限元模型（θ＝10°）Fig.6 Finite element model of positive graded auxetic honeycombs

图7 负梯度负泊松比蜂窝试件的有限元模型（θ＝10°）Fig.7 Finite element model of negative graded auxetic honeycombs

1.3 模型的可靠性分析

为了验证有限元模型的可靠性，本文首先计算了一个均匀正六边形蜂窝材料模型（9×6）在准静态压缩（v＝1m／s）下的变形特征.将本文通过有限元模拟得到的蜂窝材料变形模式与文献［14］进行对比，如图8所示.由图可知，二者的变形特征基本吻合，从而有效证明了本文有限元模型的可靠性.

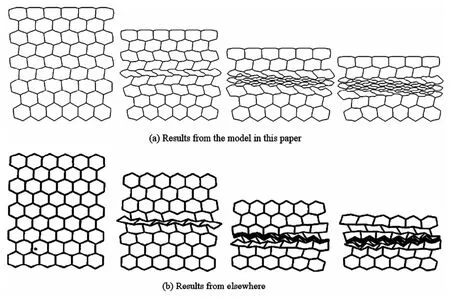
图8 正六边形蜂窝材料的面内变形模式（v＝1m／s）Fig.8 In-plane deformation modes of regular hexagon honeycombs（v＝1m／s）

2 计算结果与讨论

2.1 梯度负泊松比蜂窝材料的动态响应

图9和图10给出了三种初始冲击速度下具有不同胞元凹角的正负梯度负泊松比蜂窝试件在ε＝0.36时的面内变形模式.由图可知，当胞元凹角较小（θ＝10°和θ＝15°）时，在低速冲击（v＝50m／s）下，蜂窝试件两边自由端的胞元受拉，而纵向对称轴附近的中部胞元受压，因此容易出现局部变形带.随着胞元凹角的增大（θ＝20°和θ＝25°），由于塑性铰在节点处出现，更容易呈现整体收缩变形的模式，正梯度蜂窝（Δt＞0）从冲击端开始被压缩密实，而负梯度蜂窝（Δt＜0）的固定端先被压实.

当冲击速度增加到100m／s时，胞元凹角较小（θ＝10°和θ＝15°）的正梯度蜂窝试件的变形主要集中在冲极端，而胞元凹角较大（θ＝20°和θ＝25°）的蜂窝试件在冲击端表现为‘I’型剪切变形模式，同时试件发生整体收缩变形.对负梯度蜂窝来说，胞元凹角较小（θ＝10°和θ＝15°）的蜂窝试件在冲击端表现为‘I’型剪切变形模式，同时固定端附近由于相对密度小，也会发生局部变形，胞元凹角较大的蜂窝试件（θ＝20°和θ＝25°）首先在冲击端呈现型剪切变形模式，随后试件发生整体收缩变形.

当冲击速度达到120m／s时，惯性效应增强，正梯度蜂窝的变形主要集中在冲极端，而负梯度蜂窝在冲击端表现为‘I’型剪切变形模式，同时在固定端附近（低密度区）发生局部变形.由此可见，在动态冲击作用下，梯度、胞元内凹角度和冲击速度都是厚度梯度型负泊松比蜂窝材料变形模式的主要影响因素.

图9 正梯度负泊松比蜂窝材料在三种冲击速度下的变形模式Fig.9 Deformation modes of positive graded auxetic honeycombs under three impact velocities

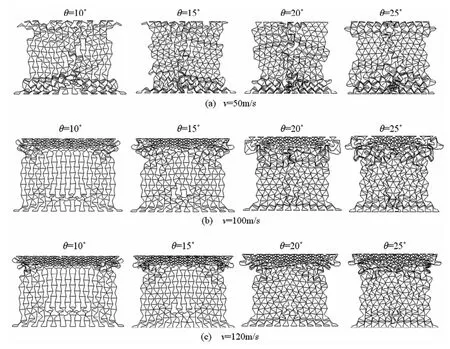
图10 负梯度负泊松比蜂窝材料在三种冲击速度下的变形模式Fig.10 Deformation modes of negative graded auxetic honeycombs under three impact velocities

具有不同胞元凹角的正负梯度负泊松比蜂窝材料在三种初始冲击速度下的动态响应曲线如图11所示，由于变形规律基本一致，这里只给出了θ＝10°的曲线作为说明.由图可见，梯度负泊松比蜂窝在冲击荷载作用下的动态响应规律为：最初响应接近线性，直到试件中蜂窝单元的局部应力超过胞壁的弹性屈曲极限，达到试件的初始应力峰值；随后进入稳定的平台区.在冲击速度较低（v＝50m／s）时，蜂窝试件不会发生致密化变形，即材料的应力值不会随着应变值的增加而迅速增大.这是由于负泊松比材料在受到压缩时会发生横向收缩变形，横向抗压面积减小，抗压强度增大，所以在初始冲击速度较小时，其冲击能量不足以使试件最终发生破坏.随着冲击速度的增加，试件最终会被压溃，进而发生致密化变形，材料在最后会再次达到初始应力峰值.

图11 梯度负泊松比蜂窝材料在三种冲击速度下的应力应变曲线（θ＝10°）Fig.11 Nominal stress-strain curves for graded auxetic honeycombs under three impact velocities（θ＝10°）

2.2 梯度负泊松比蜂窝材料的能量吸收性能

在冲击作用下，平台应力（plateau stress）和比吸收能量（specific absorbed energy）是与多孔材料能量吸收关系最大的两个指标［15］.平台应力可由应力-应变曲线平台阶段的应力取平均值得到：

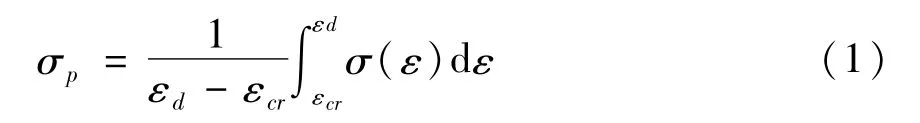
式中εcr为屈服应变，即初始应力峰值所对应的名义应变；εd为锁定应变（压实应变），是材料被压缩密实前的最大应变；σ（ε）为随名义应变而变化的名义应力.

比吸收能量（即质量能量吸收率）可定义为［16］：

表4给出了三种初始冲击速度下，具有不同胞元凹角的均匀和梯度负泊松比蜂窝材料在冲击端的平台应力.数据显示，冲击速度越大，梯度负泊松比蜂窝在冲击端的平台应力也越大.冲击速度较低（v＝50m／s）时，正负梯度蜂窝和对应的均匀负泊松比蜂窝的平台应力大小相差不大.高速冲击（v＝100m／s和v＝120m／s）下，正梯度蜂窝的平台应力小于负梯度蜂窝和均匀负泊松比蜂窝，这是由于梯度蜂窝结构在冲击压缩初期的初始峰值应力小于均匀蜂窝结构.对负梯度蜂窝来说：（1）在冲击速度为v＝100m／s时，其平台应力小于均匀负泊松比蜂窝；（2）在冲击速度达到v＝120m／s时，胞元扩张角较小（θ＝10°和θ＝15°）的负梯度蜂窝的平台应力略大于均匀蜂窝，而胞元扩张角较大（θ＝20°和θ＝25°）的负梯度蜂窝的平台应力小于均匀蜂窝.可见，梯度、胞元凹角和冲击速度均能影响梯度负泊松比蜂窝材料的平台应力.如果能正确选取梯度负泊松比蜂窝材料的各项参数，那么会有效地降低初始应力峰值，进而起到保护构件的作用.

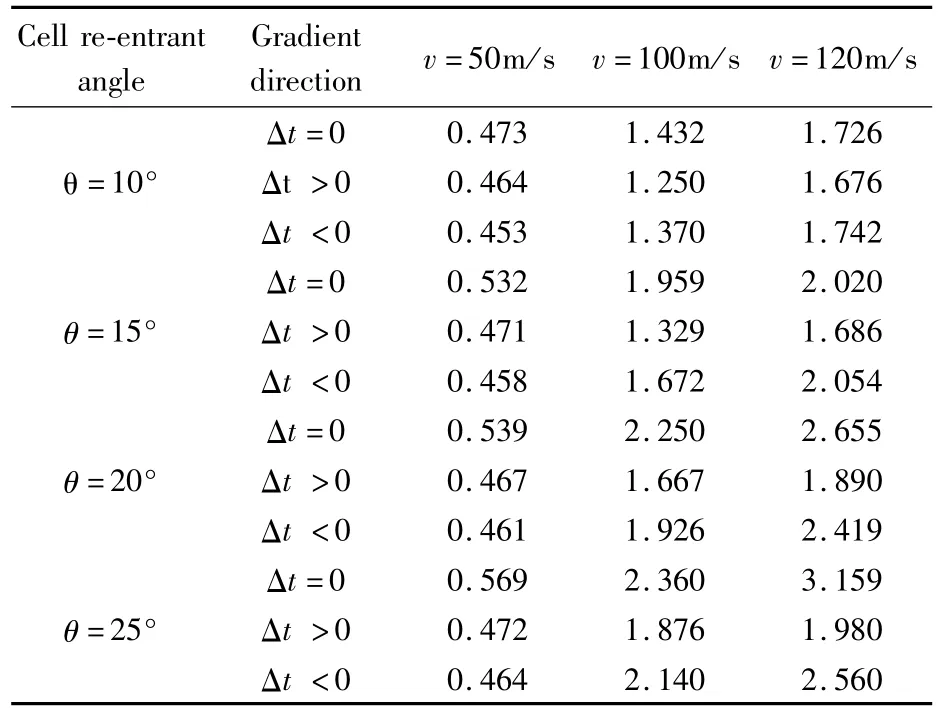
表4 负泊松比蜂窝材料在三种冲击速度下的平台应力（单位：MPa）Table 4 Plateau stress for auxetic honeycombs under three impact velocities（unit：MPa）

在三种初始冲击速度下，均匀负泊松比蜂窝和梯度负泊松比蜂窝的单位质量能量吸收率与名义应变之间的关系曲线如图12所示.由图可知，在胞元凹角和冲击速度相同的情况下，负梯度蜂窝的能量吸收能力在前期大于正梯度蜂窝和均匀负泊松比蜂窝，随着压缩量的增加，其能量吸收能力逐渐减弱，并且在后期小于正梯度蜂窝和均匀负泊松比蜂窝.正梯度蜂窝的能量吸收能力在前期小于负梯度蜂窝和均匀负泊松比蜂窝，但是随着冲击的持续，其能量吸收能力在后期大于负梯度蜂窝和均匀负泊松比蜂窝.这是由于正梯度蜂窝的变形模式是由低密度区向高密度区变形，因此初期吸能能力较差；而负梯度蜂窝的冲击压缩变形是从高密度区开始的，所以试件的初始能量吸收能力就很强，从而说明蜂窝材料的压缩变形模式影响其能量吸收效果.在梯度和冲击速度相同的情况下，胞元凹角越小，则其能量吸收能力越强.在胞元凹角和梯度一定时，冲击速度越大，厚度梯度型负泊松比蜂窝的能量吸收能力越强.可见，厚度梯度型负泊松比蜂窝材料的能量吸收能力与梯度、胞元凹角和冲击速度有关.

图12 梯度负泊松比蜂窝材料在三种冲击速度下的质量能量吸收率Fig.12 Energy absorption permass for graded auxetic honeycombs under three impact velocities

3 结论

本文研究了具有密度梯度的负泊松比蜂窝材料在不同初始冲击速度下的力学行为，从变形模式、动态响应曲线及能量吸收方面，探讨它们的面内冲击动力学性能.

厚度梯度型负泊松比蜂窝材料的平台应力和能量吸收能力的主要影响因素是梯度、胞元凹角和冲击速度：

（1）梯度和胞元凹角一定时，蜂窝在冲击端的平台应力随速度的增加而增大.

（2）在冲击速度相同时，正梯度蜂窝的平台应力始终小于具有相同胞元凹角的均匀负泊松比蜂窝.负梯度蜂窝的平台应力还与胞元内凹角度的大小有关：在冲击速度较低（v＝50m／s）时，其平台应力与对应的均匀负泊松比蜂窝大小相差不大；在冲击速度为v＝100m／s时，其平台应力小于均匀负泊松比蜂窝；在冲击速度达到v＝120m／s时，胞元凹角较小（θ＝10°和θ＝15°）的负梯度蜂窝的平台应力略大于均匀负泊松比蜂窝，而胞元凹角较大（θ＝20°和θ＝25°）的负梯度蜂窝的平台应力小于均匀负泊松比蜂窝.

（3）在胞元凹角和冲击速度一定的情况下，负梯度蜂窝的能量吸收能力在前期较强，但是会随着压缩量的增加逐渐减弱，并在后期小于正梯度蜂窝和均匀负泊松比蜂窝；正梯度蜂窝的能量吸收能力在前期小于负梯度蜂窝和均匀负泊松比蜂窝，但是随着冲击的进行，其后期能量吸收能力大于负梯度蜂窝和均匀负泊松比蜂窝.

（4）梯度和冲击速度相同时，胞元凹角越小，厚度梯度型负泊松比蜂窝的能量吸收能力越强.

（5）在梯度和胞元凹角一定的条件下，当冲击速度增大时，厚度梯度型负泊松比蜂窝的能量吸收能力也会随之增强.

如果能适当选取厚度梯度型蜂窝材料的各项参数，那么就能在工程应用中有效地实现降低初始应力峰值、保护构件和提高材料能量吸收能力的目的.可见，具有密度梯度的负泊松比蜂窝材料在结构防护方面具有良好的应用前景.

1 Banhart J.Manufacture，characterization and application of cellular metals and metal foams.Progress in Materials Science，2001，46（6）：559～632

2 Yang W，Li ZM，Shi W，Xie BH，Yang M B.Review on auxetic materials.Journal of Materials Science，2004，39（10）：3269～3279

3 Frost H J，Ashby M F.Deformation mechanism maps：the plasticity and creep of metals and ceramics.Pergamon press，1982

4 Lakes R S.Foam structures with a negative Poisson′s ratio.Science，1987，235（4792）：1038～1040

5 卢子兴，赵亚斌.一种有负泊松比效应的二维多胞材料力学模型.北京航空航天大学学报，2006，32（5）：594～597（Lu Z X，Zhao Y B.Mechanical model of two-dimensional cellular materials with negative Poisson′s ratio.Journal of Beijing University of Aeronautics and Astronautics，2006，32（5）：594～597（in Chinese））

6 卢文浩，鲍荣浩.动态冲击下蜂窝材料的力学行为.振动与冲击，2005，24（1）：49～53（Lu W H，Bao R H.Mechanical analysis of the impacted honeycombs.Journal of Vibration and Shock，2005，24（1）：49～53（in Chinese））

7 张新春，刘颖，李娜.具有负泊松比效应蜂窝材料的面内冲击动力学性能.爆炸与冲击，2012，32（5）：475～482（Zhang X C，Liu Y，Ni L.In-plane dynamic crushing of honeycombs with negative Poisson′s ratio effects.Journal of Explosion and Shock Waves，2012，32（5）：475～482

8 Koizumi M.FGM activities in Japan.Composites Part B：Engineering，1997，28（1-2）：1～4

9 Shim PW，Stronge W J.Lateral crushing in tightly packed arrays of thin-walled metal tubes.International Journal of Mechanical Science，1986，28（10）：709～728

10 Hu L L，Yu TX，Gao ZY，et al.The inhomogeneous deformation of polycarbonate circular honeycombs under inplane compression.International Journal of Mechanical Science，2008，50（7）：1224～1236

11 Karagiozova D，Yu T X.Post-collapse characteristics of ductile circular honeycombs under in-plane biaxial quasistatic and low-velocity impact loading.International Journal of Mechanics Science，2005，47（4／5）：570～602

12 刘颖，何章权，吴鹤翔，张新春.分层递变梯度蜂窝材料的面内冲击性能.爆炸与冲击，2011，31（3）：225～231（Liu Y，He ZQ，Wu H X，Zhang X C.In-plane dynamic crushing of functionally layered metal honeycombs.Journal of Explosion and Shock Waves，2011，31（3）：225～231（in Chinese））

13 张新春，刘颖.密度梯度蜂窝材料动力学性能研究.工程力学，2011，29（8）：372～377（Zhang X C，Liu Y.Research on the dynamic crushing of honeycombs with density gradient.Journal of Engineering Mechanics，2011，29（8）：372～377（in Chinese））

14 PaPka S D，Kyriakides S.In-plane compressive response and crushing of honeycombs.Journal of the Mechanics＆Physics Solids，1994，42（10）：1499～1532

15 Gibson L J，Ashby M F.Cellular solids：Structure and properties.2nd ed.Cambridge：Cambridge University Press，1997：87～148

16 Kooistra GW，Deshpande V S，Wadley HNG.Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminum.Acta Materialia，2004，52（14）：4229～4237

Received 5 October 2015，revised 29 June 2016.

*The project supported by the National Natural Science Foundation of China（11402035），Doctoral Fund of Ministry of Education（20130205110014）

†Corresponding author E-mail：lflanmeng＠163.com

DYNAMIC CRUSHING PERFORMANCE OF GRADED AUXETIC HONEYCOMBS WITH NEGATIVE POISSON′S RATIO*

Yin Guansheng1Yao Zhaonan2†
（1.School of Science，Chang’an University，Xi′an 710064，Shanxi，China）（2.China Gezhouba Group CO，LTD Survey and Design Institude，Wuhan 430000，China）

Based on the concept of functionally graded materials（FGM）and through changing the wall thickness of honeycombs cell，a model for density graded re-entrant auxetic honeycombs is established by using the nonlinear finite element program LS-DYNA.The deformation modes，dynamic response and energy absorption characteristics of both the homogeneous and graded auxetic honeycombs under different in-plane impact velocities are examined and compared.Results indicate that the dynamic responses and energy absorption ability of graded auxetic honeycombs change with the gradient，cell re-entrant angle and impact velocity.Given proper parameters，the initial peak stress can be decreased，but the energy absorption ability is still kept well.Therefore，auxetic honeycombs with density gradient and negative Poisson′s ratio can be widely applied in structural protection areas.

density gradient，auxetic honeycombs，functionally graded materials（FGM），dynamic crushing，mechanical properties

10.6052／1672-6553-2016-030

2015-10-05收到第1稿，2016-06-29收到修改稿.

*国家自然科学基金青年科学基金项目（11402035），教育部博士点基金（20130205110014）（博导类）

†通讯作者E-mail：lflanmeng＠163.com