几种随机相互作用势相关的交通流模型比较*
郑伟范邓绯江宝山殷中慧张继业†
(1.西南交通大学牵引动力国家重点实验室,成都 610031)
(2.西南交通大学信息化研究院,成都 610031)
(3.四川职业技术学院,遂宁 629000)
几种随机相互作用势相关的交通流模型比较*
郑伟范1,2邓绯3江宝山1殷中慧1张继业1†
(1.西南交通大学牵引动力国家重点实验室,成都 610031)
(2.西南交通大学信息化研究院,成都 610031)
(3.四川职业技术学院,遂宁 629000)
为了研究随机因素对交通流的影响,人们提出了几种考虑顾前相互作用势的交通流模型.它们均基于简单非对称排斥过程和微观动力学模型,对于描述交通流的随机演化行为具有优越性.本文对几种势相关的交通流模型进行比较,特别是比较不同模型的车辆状态迁移的概率计算机制;进而通过数值仿真,比较不同模型刻画的随机演化现象.通过本文的比较,得到几种随机相互作用势相关的交通流模型的流量-密度图、时空斑图以及三维演化结果.为进一步优化势函数结构,建立符合实际交通的随机交通流模型奠定基础.
交通流,相互作用势,随机,模型,比较
引言
随着交通基础设施建设与交通系统的不断发展,人们出行和道路交通需求不断增加,现有的交通管理、控制方法不能满足道路交通的发展需要,交通拥塞等问题日益严重[1-2].由于交通流受到多种随机因素,如气候、雨、雪等外部因素,以及道路交通环境、司机驾驶行为、车辆个体特性等内部因素的共同影响,交通流随机演化行为的研究对于掌握交通流的随机演化规律,并以此指导交通系统的整体控制、组织和管理具有重要作用.由于确定性的建模方法缺乏描述可能性的机制,使得该类方法对于管理和捕捉高于临界密度的多值的、时变的随机动态演化行为和规律存在困难.人们开始将随机噪声项引入到保守方程中而产生了基于随机过程序列的交通流模型[3-4].后来进一步将噪声项引入到动力学速度方程及速度-密度关系中[5-6].Chen总结了交通流随机性研究的四个主要方面[7]:(1)对一阶保守方程或高阶方程进行随机化的宏观交通流模型;(2)对驾驶行为或混合交通流进行随机化的微观交通流模型;(3)对流量、密度、速度相互关系图或相应相变进行随机化的研究;(4)对道路通行能力或通行时间分布进行随机化的交通可靠性研究.这些模型需要假设噪声项满足某种随机过程,而实际交通中,这种假设并不一定完全符合.
考虑随机慢化的元胞自动机模型是另一种研究交通流随机性的方法.该方法最早是由Cremer和Ludwig[8]将元胞自动机(Cellular Automata:CA)引入到交通流的研究中.然而,1992年Nagel和Schreckenberg提出的模型(简称为NS模型)[9],使得CA交通流模型受到广泛关注.该类模型本质上采用离散空间和时间的元胞自动机,通过一定的规则自动演化,对于描述实际的交通流现象具有独特的优势,近年来开始广泛应用于交通流问题的研究.贾斌等[10]总结了2007年以前基于元胞自动机模的交通流建模与模拟进展.
上述元胞自动机模型多采用常数值的随机慢化概率,实际上只是加入了随机噪声、可能性和偏好的确定性模型[11],对随机现象的描述能力有限.为了更好地描述高密度交通流中的随机现象,人们开始考虑车辆间、车辆与环境间的相互作用对司机决策的影响,建立了随机相互作用势相关的交通流模型.Sopakis和Katsoulakis[12]基于非对称排斥过程、Ising模型[13-14]、Arrhenius微观动力学方法[15],及动态计算车辆状态的迁移率,提出了一种势强度相关的随机交通流模型,简记为AM模型.这里的势能指司机能够感知到的自身车辆前面顾前长度内多个元胞中的车辆产生的影响,即顾前势.该模型通过蒙特卡洛仿真,再现了自由流、同步交通、运动波、“时走时停”现象以及多样的高密度交通行为.之后的2008年,Sopakis等进一步将该模型应用于多车道的情况[16].2012年,Hauck[17]在相互作用强度(势强度)为常数的情况下,研究了AM模型的统计特征.2013年,AM模型被扩展应用到无网格情况[18].基于AM模型,文献[19]提出了可变慢化概率的交通流模型,简记为VP模型,改进了现有CA模型中的随机慢化概率为常数值的计算过程.文献[20]进一步考虑司机受到前面越近的车辆影响越大的事实,提出了考虑加权系数的顾前势交通流模型,简记为WP模型.适当改善了AM模型中势强度为常数的不足.然而,上述势相关模型中,相互作用势函数采用了常数和离散函数的形式.实际交通中,司机感受到的前面车辆的相互作用是依据车辆间的距离等因素连续动态变化的.需要建立连续的势函数,更好地描述随机因素对交通流的连续动态影响.Ni Daiheng[21-22]提出的势场模型中虽然没有给出具体的表达式,但是指出了势函数可以采用类似Lennard-Jones势函数[23]的形式.将连续的Lennard-Jones势函数引入AM模型中,可以得到基于Lennard-Jones势的交通流模型,简记为LJ模型.
综上所述,基于相互作用势的模型对于描述交通流的随机演化行为具有优越性.本文对最近的几种模型进行比较,特别是比较不同模型的车辆状态迁移的概率计算机制;进而通过数值仿真,比较不同模型所刻画的随机演化现象.
1 交通流的随机相互作用势建模过程
交通流随机相互作用相关的模型,如AM、WP和LJ模型等,考虑司机能够感知到的前面车辆对自身的相互作用,可以很好地描述高密度交通流的复杂非线性现象.这类模型主要采用统计物理学中的Ising模型[13-14]的格子划分与描述方法,采用一定的边界条件和初始条件,对交通系统的物理对象进行描述.通过序参量的定义,基于非对称简单排斥过程等,建立交通系统道路占用状态的描述过程.并基于随机动力学的理论方法,来计算车辆运动状态的迁移概率和迁移率.建模过程主要包括交通系统的物理道路划分、车辆微观相互作用的状态描述,以及动力学系统的选择步骤.
1.1 交通系统的物理道路划分
考虑单类车辆在单车道公路上沿一个方向的运动,道路的物理划分主要依据Ising模型的格子划分方法,定义一维格子L={1,2,…,N},N>1空间元胞(N为格子总数);参考文献[11-12]的方法,定义二维格子,可以扩展到适合多车道的情况.
1.2 车辆微观相互作用的状态描述
系统的相互作用状态由序参量函数σ:L×R+→{0,1}N确定.对任意时间t∈R+和x∈L,σ(x)∈{0,1},表示有车在格点位置x为1,无车在格点位置为0.车辆配置的序参量是空间配置∑{0,1}N的一个元素.即:

与Ising系统的Arrhenius动力学模型相似,可以计算车辆间的相互作用势能.这个势能能够进一步扩展到包含外部势,其可以被解释为空间或时间的占用、外部影响和交通变化等.令相互作用势能U(x,σ)有如下形式:

其中,J表示车辆间的短程相互作用势,
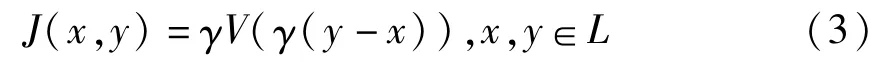
其中,γ=1/(2l+1)是描述微观交互范围的参数,l表示势半径.仿真中设定:

其中,J0为基于描述排斥、吸引或无相互作用的标记符号的参数,相当于相互作用强度.其余参数的意义及范围与AM模型相同.
假定车辆在交通中不能向后退,沿车辆前行方向移动,且相互作用只影响局部,只有一个车辆在同一时刻占据一个元胞.采用周期边界条件,使得对任意x∈L和整数m,σ(mN+x)=σ(x).
1.3 动力学系统选择
模型中序参量状态的改变是车辆运动机制的描述.物理上,AM模型的建模机制描述了车辆由一个占据格点到一个空格点的运动(扩散).由于一个格点不能被多于一个车辆同时占有(排斥原理),序参量的状态以速率c(x,y,σ)进行交换,这样细致平衡条件得到满足,如文献[12]所述.车辆的运动过程遵守排斥过程的规律[24]:每次迁移交换两个相邻格点的状态值,且车辆不允许运动到被占据的格点.格点只允许向运动方向前移到下一个格点,这样交换的仅有可能结构是如下形式:

根据文献[12]的描述,相邻两个格点的状态转换,以Arrhenius动力学的形式描述,其转换速率可计算如下:

相关参数为:c0=1/τ0,其中,τ0为弛豫时间.上式描述了在时间间隔[t,t+Δt]内,格点x与y之间的转子交换概率为:

基于该概率,即可描述司机对于车辆运动或不运动(或减速)的决策过程.通过上述过程,采用蒙特卡洛等随机过程模拟方法等,可以模拟交通流系统的复杂随机行为.
2 相互作用势相关模型比较
本节主要讨论基于相互作用势的AM模型、WP模型及LJ模型之间的不同,特别是其建模过程中的概率计算机制的不同.为了方便比较,也将NS模型的结果一并进行比较.
2.1 NS及其改进模型的概率计算机制
NS模型中,如果车辆的速度vi≥0,则在随机慢化过程中会以固定的概率p减速一个单位.这里的p是人为设定好的.实测数据显示,城市交通的随机慢化概率高于高速路交通[24].一般情况下,高速路交通中,慢化概率为p=0.2.该模型中,尽管概率p描述了交通流的随机行为,但实际交通中,司机的减速决策过程是受到车辆间相互作用而动态作出的.因此,用固定的概率值存在不足,需要进一步研究概率的计算方法.
2.2 AM模型的概率计算机制
基于非对称排斥过程、Arrhenius动力学,AM模型由一个粒子从一个状态变为另一个状态时不得不克服的能量障碍来驱动.该能量障碍由公式(2)计算每辆车的相互作用势能来得到.只有当该势能高于设定的阈值时才进行移动.在仿真过程中,由公式(4),J0>0是相互作用强度参数,由其不同的符号表示吸引、排斥或没有相互作用.因此,势函数可以改写如下:

这样,道路元胞格子的状态转换概率变为:
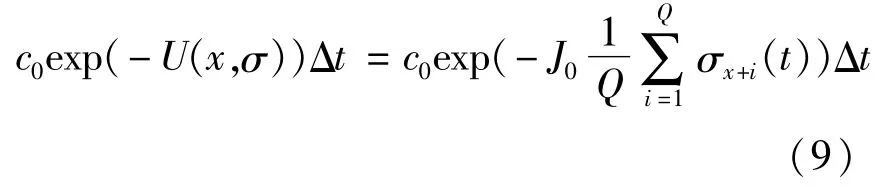
由(8)~(9)可知,势强度采用简单常数的形式,则在高密度情况下,元胞x前面顾前长度内的格子被车辆占据,不同远近位置格点上的车辆对势能的计算具有相同的贡献.换言之,远近不同位置格点上的车辆对元胞x点处的车辆的影响是一样的.这不符合实际交通中司机随机减速的决策过程中受到前面越近车辆的影响越大的事实.
2.3 WP模型的概率计算机制
WP模型通过引入加权系数,对越靠近司机的车辆的相互作用强度赋予越大的权重.势函数可表示如下:

这样,元胞格子的状态转换概率可由下式计算:

其中,wi是顾前长度内第i个元胞的权系数.在仿真中,权系数可取形如wi=2wi+1的形式.
WP模型引入了距离相关的势函数,建模过程更符合实际交通中司机基于前面车辆和道路环境情况进行随机决策的过程.然而,AM模型与WP模型中的势函数均为离散函数.实际交通中,司机感受到的前面车辆的相互作用势是随车辆间的距离连续变化的.因此,相互作用势函数应该采用连续函数的形式.
2.4 LJ模型的概率计算机制
与NS模型、AM模型及WP模型不同,Ni Daiheng提出的模型中,(4)式采用连续的势函数形式.但其表达式是没有具体给出,只说明可以采用如下类似Lennard-Jones势的形式[22].

其中,d表示两个粒子(即车辆)间的距离,ε为势阱深度,d0表示两个粒子间相互作用力为零的临界距离.
Lennard-Jones势反映了两个方面的相互作用关系,一是长程相互吸引作用,类似于司机按期望速度驾驶的动机;二是短程相互排斥作用,类似于车辆间的相互影响.
这里我们采用指数参数为12-6的形式,主要是因为该种形式应用广泛,且便于计算.这样,进一步将(12)式的势函数引入(8)和(9)中,得到LJ模型的车辆状态转移概率的计算式子如下:

3 数值仿真结果
本节介绍上述NS、AM、WP、LJ模型在Matlab下的仿真结果.实验采用一段长度固定的环形道路来对实际道路进行模拟,长度为n=500个元胞(即500*7.5=3750m).采用周期性边界条件,车辆假定在该格子路段上运行一定的时间步,时间间隔Δt取1s.密度和速度依据道路上车辆的初始分布进行统计平均.为了消除初始扰动的影响,实验运行2000s,并取后500s的数据结果.
3.1 交通流流量、密度、速度关系对比
相关实验参数条件为顾前长度Q=5;相互作用势强度J0=6;Vmax=5元胞/秒;NS模型下的慢化概率p=0.2;LJ模型的势井深度ε=0.01,临界距离d0=20m;WP模型中,比例加权系数为2,即wi=2wi+1.AM、WP、LJ及NS模型的流量、密度和速度关系如图1所示.

图1 四模型交通流流量、速度和密度相互关系图Fig.1 Relationships among flow,speed and density for four models
由于不同的随机慢化概率计算机制不同,导致司机加减速的决策结果不同,因而得到的不同模型的交通流量、密度和速度等有所不同.由图1(a)可知,对于临界密度和临界最大流量,趋势是AM模型<WP模型<LJ模型;在超过临界密度的高密度区域,对应同一交通密度下的交通流量趋势是AM模型<WP模型<LJ模型.由图1(b)可知,在高于临界密度后,同一速度下的交通流量趋势是AM模型<WP模型<LJ模型.由图1(c)可知,在高于临界密度后,同一速度下的交通密度趋势是AM模型<WP模型<LJ模型.由于NS模型没有考虑相互作用势,不同的慢化概率可以得到不同的临界密度、临界最大流量和高密度曲线.由此可见,相互作用势相关模型对高密度的交通流量有所改善,改善效果趋势为AM模型<WP模型<LJ模型.
并且,由图1(a)可知,在自由流阶段,NS、AM、WP和LJ四种模型的流量-密度曲线基本重合;由此可见,相互作用势对低密度的交通流影响不大.
3.2 四模型三维时空演化结果对比
实验参数条件如图1所示,且全部模型的车辆初始分布密度为0.16辆/元胞,得到的密度-空间-时间三维图如图2所示.

图2 四模型密度-空间-时间三维图Fig.2 3D plots of density-space-time for four models
由图2的四个图可知,NS模型的密度峰值无序出现,且出现较多,尚未形成密度波;AM模型的密度波趋于有序;WP模型的密度波有序性进一步增加,波峰数减少;LJ模型密度波最有序,且数量最少.四个模型的三维演化图中密度波峰值出现的有序性趋势为(a)<(b)<(c)<(d),即NS模型<AM模型<WP模型<LJ模型.由此可知,考虑相互作用势的模型对随机短时拥堵交通流有所改善,表现为三维图中的密度波峰趋于有序出现.
3.3 四模型斑图对比
进一步比较四个模型的二维时空斑图,实验参数条件如图1所示,车辆初始分布密度均取0.18辆/元胞,得到的结果如图3所示.

图3 四个模型的时空斑图Fig.3 Space-timepatterns of four models
由图3的时空斑图可知,短时堵塞(图中点聚集处)出现的有序性趋势为 (a)<(b)<(c)<(d),即NS模型<AM模型<WP模型<LJ模型.除了NS模型会出现较多的各种随机短时堵塞外,其它三种模型均不易出现随机短时堵塞状态.AM、WP和LJ模型中,LJ模型的短时堵塞持续时间最短,且短时堵塞区域相对最少,表现为斑图中的聚集黑色线条最少;而且LJ模型斑图中有三相状态的出现,在其他模型的斑图中则未出现.比较四种模型的斑图,进一步验证了图2的结论.
初步分析出现图2和图3中结果的原因,主要是由于考虑相互作用势的情况下,司机的慢化决策过程是依据司机前方顾前势范围内的车辆及道路状态动态做出的.这样就避免了固定概率情况下可能会出现前方道路有足够的空格时由于满足概率条件而产生的不必要的减速过程.由AM、WP和LJ模型的势函数结构可知,AM模型改善了NS模型中慢化概率为常数的情况.WP模型进一步刻画顾前势与距离的关系,改善势函数为常数的情况.LJ模型中前方车辆的距离参数直接作为势函数的参数,直观体现不同距离的车辆对司机的影响.因此,由于不同模型的势函数的结构不同,出现了图2的三维演化结果和图3的时空斑图的差异.由此可知,势函数的结构会敏感地影响交通流的行为.
4 结论
本文对目前研究中提出的几种相互作用势相关的交通流模型进行比较,特别是比较每种模型中描述交通流随机行为的车辆状态迁移的概率计算机制.包括势强度相关的AM模型、离散加权势相关的WP模型和连续加权势相关的LJ模型.分别对几种不同势函数的交通流模型进行仿真,得到几种随机相互作用势相关的交通流模型的流量-密度图,时空斑图、以及时间、空间和密度三维演化结果.
通过比较可以得到如下结论:相互作用势相关模型能够刻画高密度的交通流随机演化现象.势相关模型对高密度的随机短时拥堵交通流有所改善,交通流量改善效果趋势为AM模型<WP模型<LJ模型.势函数的结构会敏感地影响交通流的行为.相互作用势对低密度的交通流影响不大.
通过本文的比较,可以为进一步优化势函数,建立符合实际交通的随机交通流模型奠定基础.
1 Kittelson,Associates.Transit capacity and quality of service manual.Washington:Transportation Research Board Press,2003:7~22
2 Kerner B S,Rehborn H.Experimental properties of phase transitions in traffic flow.Physical Review Letters,1997,79(20):4030~4033
3 Gazis D C,Knapp CH.On-line estimation of traffic densities from time-series of flow and speed data.Transportation Science,1971,5(3):283~301
4 Szeto M W,Gazis D C.Application of Kalman filtering to the surveillance and control of traffic systems.Transportation Science,1972,6(4):419~439
5 Wang Y,Papageorgiou M.Real-time freeway traffic state estimation based on extended Kalman filter:a general approach.Transportation Research Part B:Methodological,2005,39(2):141~167
6 Wang Y,Papageorgiou M,Messmer A.Real-time freeway traffic state estimation based on extended kalman filter:A case study.Transportation Science,2007,41(2):167~181
7 Chen X Q,Li L,Shi Q.Stochastic Evolutions of Dynamic Traffic Flow:Modeling and Applications.Berlin:Springer,2014:1~25
8 Cremer M,Ludwig J.A fast simulation model for traffic flow on the basis of Boolean operations.Mathematics and Computers in Simulation,1986,28(4):297~303
9 Nagel K,Schreckenberg M.A cellular automaton model for freeway traffic.Journal de Physique I,1992,2(12):2221~2229
10 贾斌,高自友,李克平,李新刚.基于元胞自动机的交通系统建模与模拟.北京:科学出版社,2007:70~149(Jia B,Gao Z Y,Li K P,Li X G.Models and simulations of traffic system based on the theory of cellular automaton.Beijing:Science,2007:70~149(in Chinese))
11 Sopasakis A,Katsoulakis M A.Stochastic modeling and simulation of traffic flow:asymmetric single exclusion process with Arrhenius look-ahead dynamics.SIAM Journal on Applied Mathematics,2006,66(3):921~944
12 Sopasakis A.Stochastic noise approach to traffic flow modeling.Physica A:Statistical Mechanics and its Applications,2004,342(3):741~754
13 Kipnis C,Landim C.Scaling limits of interacting particlesystems.Springer Science&Business Media,Berlin Heidelberg,1999:257~346
14 Liggett T.Interacting particle systems.Springer Science&Business Media,Berlin Heidelberg,2005:122~224
15 Vlachos D G,Katsoulakis M A.Derivation and validation of mesoscopic theories for diffusion of interacting molecules.Physical Review Letters,2000,85(18):3898~3901
16 Alperovich T,Sopasakis A.Stochastic description of traffic flow.Journal of Statistical Physics,2008,133(6):1083~1105
17 Hauck C,SUN Y,Timofeyev I.On cellular automata models of traffic flow with look-ahead potential.Stochastics and Dynamics,2014,14(3):1350022
18 Sopasakis A.Traffic updating mechanisms for stochastic lattice-free dynamics.Procedia-Social and Behavioral Sciences,2013,80:837~845
19 Zheng W F,ZHENG JY.A cellular automata model of traffic flow with variable probability of randomization.Chinese Physics B,2015,24(5):058902
20 郑伟范,张继业,王明文,等.具有加权顾前势的交通流模型.物理学报,2014,63(22):228901-1~7(Zheng W F,Zhang JY,Wang MW,etal.On traffic flow model with weighted look-ahead potential.Acta Physica Sinica,2014,63(22):228901-1~7(in Chinese))
21 Ni D.Multiscale modeling of traffic flow.Mathematica Aeterna,2011,1(1):27~54
22 Ni D.A Unified Perspective on Traffic Flow Theory,Part I:The Field Theory.Applied Mathematical Sciences,2013,7(39):1929~1946
23 Jones J E.On the determination of molecular fields.II.From the equation of state of a gas.In:Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.London:The Royal Society,1924:463~477
24 Knospe W,Santen L,Schadschneider A,et al.Single-vehicle data of highway traffic:Microscopic description of traffic phases.Physical Review E,2002,65(5):634~634
Received 2 June 2016,revised 19 July 2016.
*The project supported by the National Natural Science Foundation of China(11572264,11402214,61373009)
†Corresponding author E-mail:jyzhang@home.swjtu.edu.cn
COMPARISON OF SEVERAL INTERACTIONAL POTENTIAL RELATED TRAFFIC FLOWMODELS*
Zheng Weifan1,2Deng Fei3Jiang Baoshan1Yin Zhonghui1Zhang Jiye1†
(1.Traction Power State Key Laboratory,Southwest Jiaotong University,Chengdu 610031,China)
(2.Information research Institute,Southwest Jiaotong University,Chengdu 610031,China)
(3.Sichuan Vocational and Technical College,Suining,629000,China)
In order to study the influence of random factors on traffic flow,several traffic flow models considering the interaction potential are proposed.They are developed based on the simple asymmetric exclusion process and the microscopic dynamic model,and show the advantage of describing the stochastic evolution of traffic flow.Several interaction potential related traffic flow models are also compared in this paper.Especially,the computing mechanism of the vehicle state transition probability in different models are compared.Moreover,the stochastic evolutionary phenomena described in different models are compared by means of numerical simulation.The flow density diagram,spatiotemporal patterns and three-dimensional evolution results of these models are then obtained by the comparison in this paper.These results provide the foundation on further potential function optimization and the establishment of stochastic traffic flow models in accordance with actual traffic.
traffic flow,interactional potential,stochastic,model,comparison
10.6052/1672-6553-2016-042
2016-06-02收到第1稿,2016-07-19收到修改稿.
*国家自然科学基金资助项目(11572264,11402214,61373009)
†通讯作者E-mail:jyzhang@home.swjtu.edu.cn

