优化设计在汽车操纵稳定性研究中的应用

谢美芝，蒋银静，韦超毅，应文倩

优化设计在汽车操纵稳定性研究中的应用

谢美芝1，蒋银静2，韦超毅3，应文倩3

（1.广西大学土木工程学院，广西大学工程防灾与结构安全教育部重点实验室，广西南宁530004；2.广西机电职业技术学院，广西南宁530000；3.广西大学机械工程学院，广西南宁530004）

汽车的操纵稳定性直接关系到汽车的行驶安全，通过建立线性两自由度汽车模型，以车辆固有圆频率为优化目标，车辆前、后轮侧偏刚度为设计变量，阻尼比、适度不足转向为约束条件，建立优化设计数学模型。利用MATLAB优化工具箱，对某车辆进行优化，并对优化前、后车辆的性能进行时域和频域对比分析。结果表明：优化后汽车的固有圆频率提高、反应速度加快，且超调量也控制在合理的范围，为汽车操纵稳定性的研究提供了一个简捷可行的方法。

操纵稳定性；优化设计；阻尼比；固有圆频率

操纵稳定性不仅影响到汽车驾驶的操纵方便程度，而且也是决定高速汽车安全行驶的一个主要性能，被称之为“高速汽车的生命线”。随着高速公路的飞速发展，对汽车高速行驶的操纵稳定性提出了更高的要求。在研究汽车操纵稳定性时，常把汽车本身看做一个控制系统，按照对控制系统的稳定性、稳态品质和瞬态响应特性的一般要求，来分析和研究汽车的动态特性[1]。超调量、反应时间是系统动态性能中最主要的指标，但这两者是相互矛盾的。如何兼顾反应时间和超调量，将其控制在合理的范围之内，是提高汽车操纵稳定性的有效方法。

通过选择合适的设计变量及目标函数，建立优化设计数学模型，利用MATLAB优化工具箱，对车辆系统进行优化，在保证其具有良好稳定性的基础上，尽可能地提高其快速响应能力，以及在反应过程中具有良好的平稳性。

1 优化设计数学模型的建立

1.1 目标函数和设计变量

对于一个车辆操纵系统，超调量反映系统响应过程的平稳性，表示执行上的误差，反应时间则体现了执行速度的快慢，这两个因素与阻尼比ζ和固有圆频率ω0的关系是：阻尼比ζ增大，超调量减小，反应时间增大；当阻尼比一定时，固有圆频率ω0越大，反应时间越短。系统的动态性能由固有圆频率ω0与阻尼比ζ共同决定。阻尼比ζ为0.5～0.8时，既兼顾了系统的反应时间，又使系统的超调量不至于过大[2]。综上所述，具有良好稳定性的车辆，其阻尼比应在0.5～0.8之间，且固有圆频率ω0应尽可能大些[2]。

由Riekert和Schunck提出的线性二自由度模型为汽车动力学理论提供了很好的技术基础。由线性二自由度的车辆模型[3]，可以求出固有圆频率ω0如下：

式中符号的意义见附表1.

表1 某小车优化前后参数

将固有圆频率作为优化目标，从式（1）可以看出，汽车的质量m、轴距L，转动惯量Iz，前、后轮的侧偏刚度k1、k2等对目标函数都有影响。从易于实现方面进行考虑，选取汽车前、后车轮的侧偏刚度作为设计变量，即设计变量为：X=[x1，x2]T＝[k1，k2]T.

优化目标是在满足0.5≤ζ≤0.8的前提下，使ω0获得极大值，故目标函数为：

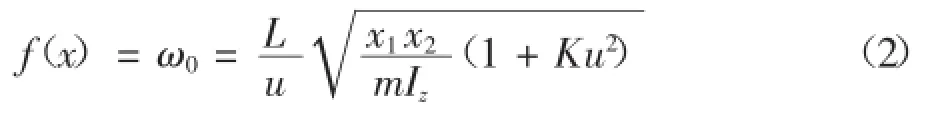
1.2约束条件的确定

约束条件可分为性能约束和边界约束两大类，由线性二自由度的车辆模型[3]，可以求出阻尼比的表达式为：

为保证0.5≤ζ≤0.8，可设约束条件为：

过多转向汽车达到临界车速时将失去稳定性，故汽车都应具有适度的不足转向，因此约束条件设为K＞0.由可得到性能约束条件为：

小型轿车轮胎的k值约为-28 000～-80 000 N/ rad范围内[3]，因此其边界约束为：

1.3优化设计数学模型

优化设计的数学模型可表示如下：

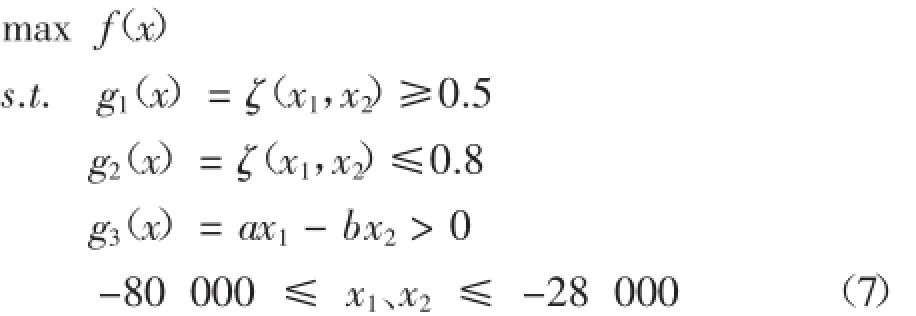
2 最优化问题的MATLAB求解

MATLAB中提供了各种各样的最优化问题求解函数，可以求解无约束最优化问题、有约束最优化问题及线性规划、二次规划问题等。式（7）为有约束非线性最优化问题，可利用MATLAB优化工具箱中的fmincon（）函数求解，该函数一般描述为：

该函数在MATLAB中的调用格式为

其中，fun为给M-函数写的目标函数，x0为初始搜索点，A、b满足线性不等式约A·x≤b，Aeq、beq满足等式约束Aeq·x＝beq，lb、ub分别为设计变量的上、下边界，各个矩阵约束如果不存在，则用空矩阵来占位。nonlcon为给非线性约束函数写的M-文件。options为控制选项。最优化运算完成后，结构将在变量x中返回，最优化的目标函数将在favl变量中返回。fmincon（x）函数常用于求多变量有约束非线性函数的最小值，因此对于求极大值的问题，需乘以-1将其转换为求极小值问题。

现利用fmincon（x）函数，根据优化设计数学模型式（7），对某小车（其参数见附表1）前、后轮的侧偏刚度进行优化。车速按被试汽车最高车速的70%并四舍五入为10的整数倍确定[4]，该车最高车速为200 km/h，故优化时的车速选为u=140 km/h.优化后车辆的前、后轮侧偏刚度分别为73 917、80 000 N/rad，优化后的阻尼比由原来的0.808降为0.66，可以看出侧偏刚度、阻尼比等均在约束范围之内，且固有圆频率也由原来的3.237 rad/s提高到3.959 rad/s，说明优化成功。

3 结果分析

3.1优化前、后转向盘角阶跃输入下的横摆角速度时域响应对比

在时域里有阶跃、单正弦两种操中输入。阶跃输入可涉及从线性区值非线性区的很广领域，是系统动力学中的重要测试函数，因此选择阶跃输入，即当车辆以恒定速度直线行驶时，驾驶员突然给转向盘一个很小的角阶跃输入。在MATLAB仿真中，根据已给的状态方程矩阵A、B、C、D和系统输入（即前轮转角）的时间序列信号，应用线性模拟函数语句lsim（A，B，C，D，delta，t）就可以方便地对汽车进行阶跃信号输入仿真，得到横摆角速度时域响应结果。

从图1中可以看出，优化前的横摆角速度超调量较小，但反应时间较长。优化后尽管超调量比优化前的要大，但没有超过120%，在合理范围之内，而反应时间却明显减小。经计算优化前的反应时间为0.39 s，优化后的反应时间为0.23 s，反应时间缩短了0.16 s，反应速度提高了41%.

图1 角阶跃输入下的时域响应对比

3.2优化前、后横摆角速度频率响应特性对比

频率响应特性完整地描述了车辆在小的扰动下的动态性能，而稳态响应则是频率响应的一个特例，因此频率响应分析在汽车操纵稳定性分析中尤为重要。在频域里进行评价时，主要评价指标有：不同频率下，横向加速度和横摆角速度对转向盘转角的增益；不同频率下，横向加速度和横摆角速度对转向盘转角的相位。一个系统传递函数G（s）的幅频和相频特性可用伯德（Bode）图来表达。在MATLAB环境下接采用bode（）命令便可得到伯德图，即

图2中，从幅频特性图可以看出，优化前的频响曲线没有明显的共振峰，即共振时增幅比较小，但也可以看出其共振频率较低只有1.81 rad/s，而优化后的尽管有了明显的共振峰，但峰值增幅只有约2 dB，在较理想的范围之内，且共振峰频率有了明显的提高，接近3.34 rad/s.从图2中的相频特性图可以看出，在0～10 rad/s的范围内，优化后的相位滞后角都有不同程度的减少。

图2 角阶跃输入下的时域响应对比

4 结束语

通过建立优化设计数学模型，利用MATLAB优化工具箱对某车辆进行优化，并对比优化前、后的性能，结果表明：优化后车辆系统的反应时间缩短了0.16 s，反应速度提高了41%，共振峰频率提高了1.53 rad/s，在0～10 rad/s的范围内，优化后的相位滞后角都有不同程度的减少，且超调量也控制在合理的范围内。在汽车操纵稳定性研究中，选择恰当的设计变量，合理设置优化目标函数和约束条件，利用MATLAB优化工具箱进行编程计算，可以获得较为满意的效果。

[1]宗长富，郭孔辉.汽车操纵稳定性的研究与评价[J].汽车技术，2000（6）：6-11.

[2]余志生.汽车理论[M].北京：机械工业出版社，2009.

[3]喻凡，林逸.汽车系统动力学[M].北京：机械工业出版社，2005.

[4]GB/T.6323.3-94.汽车操纵稳定性试验方法转向瞬态响应试验（转向盘转角脉冲输入）[S].

[5]王春香，冯慧忠.MATLAB软件在机械优化设计中的应用[J].机械设计，2004，21（7）：52-54.

[6]梁长飞，李玉光，王淑芬，等.基于Matlab汽车操纵稳定性仿真方法的研究[J].大连大学学报，2014（3）：14-18.

[7]白艳，贾鑫，宗长富，等.汽车操纵稳定性客观评价方法综述[J].科学技术与工程，2012，12（6）：1339-1347.

[8]韦超毅.根轨迹在汽车操纵稳定性研究中的应用[J].农业机械学报，2007（9）：20-25.

[9]王正林，王胜开.MATLA B/Simulink与控制系统仿真[M].北京：电子工业出版社，2012.

[10]高国燊.自动控制原理[M].广州：华南理工大学出版社，2003：62-68.

[11]Pfeffer P E，Harrer M，Johnston D N.Interaction of vehicle and steering system regarding on-centre handling[J].Vehicle System Dynam ics，2008（46）：413-428

[12]Ghoneim Y，Lin W，et al.Integrated chassis control system to enhance vehicle stability[J].International Journal of Vehicle Design，2000，23（1/2）：124-144.

The Application of Optimization Design in Vehicle Handling Stability Study

XIE Mei-zhi1，JIANG Yin-jing2，WEI Chao-yi3，YING Wen-qian3
（1.College of Civil Engineering and Architecture Guangxi University，Key Laboratory of Disaster Prevention and Structural Safety of the Ministry of Education Guangxi University，Nanning Guangxi 530004，China；2.School of Vehicle Engineering Guangxi Technological College，Nanning Guangxi 530000，China；3.School of Mechanical Engineering Guangxi University，Nanning Guangxi 530004，China）

Car’s steering stability is related to vehicle driving safety directly，the optimum design mathematical model of a car is set up through the two degrees of freedom linear model，while the inherent circular frequency of vehicle as the optimization goal，front and rear wheel cornering stiffness of vehicle as design variables，damping ratio and moderately understeer as constraint conditions.Optimization algorithm of vehicles performance is carried out by using MATLAB optimization toolbox，then compares the vehicles performances of before and after optimization in time domain and frequency domain analysis.Results show that the optimized car’s inherent circular frequency increased，reaction speed improved，and the overshoot of control in a reasonable scope，also provides a simple and feasible method for the research of vehicle handling stability.

steering stability；optimization design；damping ratio；inherent circular frequency

U461.6

A

1672-545X（2017）02-0006-03

2016-11-14

广西自然科学基金（项目编号：2014GXNSFAA118348），广西大学实验教改项目（20140118）

谢美芝（1967-），女，广西梧州人，副教授，主要研究方向：计算机仿真及CAD。