“沪港通”开通对两地股市融合的影响研究

◇潘文捷 王昕杰 陶逸清 任一平

“沪港通”开通对两地股市融合的影响研究

◇潘文捷 王昕杰 陶逸清 任一平

本文通过主成分分析和协整分析，对“沪港通”开通前后的2012年9月27日至2016年12月31日的“沪港通”成分股收盘价数据进行分析。根据本文的分析结论，“沪港通”的开通使沪、港两地股市之间的协整关系增加，且逐渐变为以同向变化为主，同向变化的趋势显著大于反向变化的趋势。

沪港通；主成分分析；协整分析

一、引言

2014年11月17日，“沪港通”正式开通；2016年12月5日，“深港通”正式开通。两种机制的实施，都是旨在更好地促进我国内地股市与国际市场的融合。本文通过时间序列模型对“沪港通”开通后沪、港两地的股市进行分析，以期对未来“深港通”以及其他类似机制的实行提出有效的建议。

二、文献综述

谷耀、陆丽娜（2006）[1]通过构建DCC-EGARCH-VAR模型，对1998年至2004年的数据进行分析，发现港股对沪、深两股都具有显著的溢出效应。石建勋、吴平（2008）[2]通过协整检验和Granger因果检验，对2003年至2007年香港的恒生指数、红筹指数、H股指数和内地的上证指数、深成指数进行分析，发现沪、深、港三地股市一体化愈加明显。胡坚、吕鹏博（2008）[3]通过协整分析，对2002年至2008年沪、港股市进行分析，发现两者未存在显著的协整关系。罗子光（2008）[4]通过协整分析和Granger因果关系检验对1998年至2007年沪、港股市指数进行分析，发现两地存在相互引导关系。丁勇锦（2008）[5]通过协整分析等模型，对2002年至2008年沪、港股市指数进行分析，发现两地股市的联动性在不断增强。鲁旭、赵迎迎（2012）[6]通过构建三元VAR-GJR-GARCH-DCC模型，对2005年至2009年香港恒生指数、上证综指和深证成指收益率进行分析，发现沪、深、港三地股市具有联动效应和趋同性。赵彦勇（2013）[7]通过非参的协整理论，对1998年至2011年沪、深、港三地股市指数数据进行分析，发现三地股市之间存在非线性关系。张仕洋（2015）[8]通过协整检验、Granger因果检验和DCC-GARCH模型，对2000年至2013年沪、深、港三地指数日收益率数据进行分析，发现三地不存在长期联动性，短期联动性正在不断加强，并且存在时变相关性。

WP Pui Han、HG Fung（2000）[9]等通过建立多元EGARCH-M模型，对沪、深、港三地股市指数进行分析，发现三地股市存在显著的波动率溢出效应。Mohamed、Fredj（2010）[10]通过非线性协整分析，对发展中国家和国际资本市场进行分析，发现发展中国家融入国际资本市场的过程是非线性、非对称并且是时变的。

从上述文献可以看出，已有不少学者对沪、深、港三地的股市进行分析，且绝大多数学者采用的数据均为上证综指、深证成指和恒生指数的收益率或收盘价。但是大多数的相关研究时间都集中在21世纪前后数年内，都在“沪港通”开通之前。本文认为，如能对“沪港通”包含的所有成分股数据进行分析，能够更好地捕捉“沪港通”带来的影响。因此，本文针对“沪港通”开通前后近四年内的数据进行时序分析，从而研究“沪港通”的开通对两地股市带来的深远影响。

三、数据选取与处理

1.数据选取

“沪港通”于2014年11月17日开通，至2016年12月31日的共同交易日共计555个交易日。为研究“沪港通”的开通给两地市场带来的影响，本文选取开通日前后各555个交易日，即2012年9月27日至2016年12月31日的股票数据，包括沪股通中全部567个成分股和港股通中全部271个成分股（已剔除已退市的中国北车），全部数据来源于雅虎财经数据库。

2.主成分分析法处理数据

本文希望能够通过分析“沪港通”中所有成分股，以更好挖掘其产生的影响，但由于股票个数过多，因此采用主成分分析法对其进行降维。

分别对“沪股通”成分股和“港股通”成分股进行主成分分析，得到前六个主成分方差贡献率如下：

表1 “沪股通”主成分贡献率

表2 “港股通”主成分贡献率

从主成分贡献率来看，两次主成分分析中，前六个主成分的累计贡献率均超过85%，说明使用前六个主成分已能较好地反映“沪股通”和“港股通”各成分股的信息。

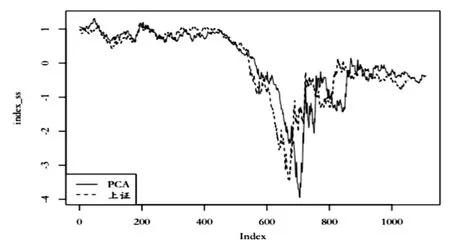
图1 标准化后PCA指数与上证指数

图2 标准化后PCA指数与恒生指数

从标准化后的主成分分析（PCA）指数分别与标准化后的上证指数、恒生指数的走势图比较来看，更进一步的说明了本文构建的主成分指数与市场指数的走势基本吻合。因此，在接下来的时序模型中，本文将对“沪股通”和“港股通”的前六个主成分指数进行分析。

四、实证分析

1.平稳性检验

为进行进一步的时序分析，需要对各主成分指数进行平稳性检验，本文主要采用ADF检验和PP检验。从以上检验结果来看，在1%显著性水平下，各主成分指数水平值的ADF检验和PP检验的p值均大于0.01，因此都是不平稳的；经过一阶差分后，各主成分指数一阶差分的ADF检验和PP检验的p值均接近于0，因此都是平稳的，即各主成分指数一阶同整，可以进行协整检验。

2.向量自回归模型最优滞后期数

为进行协整检验，我们先对向量自回归模型的最优滞后期数进行确定，该期数确定后减1即为协整检验的最优滞后期数。在Eviews中对向量自回归模型的最优滞后期数进行确定，得到结果如下：

表3 Eviews中向量自回归模型滞后期数判断结果

根据Eviews的判断结果，向量自回归模型的最优滞后期数应定为3阶，建立VAR（3）模型，根据输出的单位根表和单位根图可以看出，所有点均落在单位圆内，因此该VAR（3）模型是平稳的模型，而协整检验模型的最优滞后期数应定为2阶。

3.协整检验

对于多变量的协整检验，通常采用Johansen方法进行分析，在Eviews中包括迹（Trace）统计量和最大特征根（Maximal Eigenvalue）统计量两种方法。将数据分为“沪港通”开通前和开通后两部分，分别进行协整检验，得到结果如下：

表4 开通前协整检验结果

表5 开通后协整检验结果

由于篇幅限制，上文对Eviews的输出结果做了简化。从协整检验来看，在“沪港通”开通前，迹检验统计量显示“沪股通”和“港股通”之间存在4个协整关系，最大特征根统计量显示“沪港通”和“港股通”之间存在1个协整关系；在“沪港通”开通后，迹检验统计量显示“沪股通”和“港股通”之间存在5个协整关系，最大特征根统计量显示“沪港通”和“港股通”之间存在3个协整关系。总体来看，“沪港通”的开通使两地股市之间的协整关系变得更强。

4.协整方程

对“沪港通”开通前后的主成分指数估计长期协整方程，得到开通前的长期协整方程如下：

协整方程可以显示变量之间的长期均衡关系，对以上方程进行变换，计算得到“沪港通”开通前后两地股市之间的协整关系如下：

表6 开通前变量间长期均衡关系

表7 开通后变量间长期均衡关系

在表6、表7中，每个单元格表示“沪股通”主成分指数变动1个单位后，“港股通”主成分指数变动的方向和单位大小。

从表6、表7来看，在“沪港通”开通前，“沪股通”主成分指数变动1个单位后，“港股通”主成分指数同向变动共47.6576个单位，反向变动共53.8671个单位；而在“沪港通”开通后，“沪股通”主成分指数变动1个单位后，“港股通”主成分指数正向变动共98.6505个单位，反向变动8.1920个单位，因此，“沪港通”开通后，两地股市同向变动更为显著。

五、结论与建议

1.结论

本文通过主成分分析法对“沪港通”的所有成分股进行降维，得到“沪股通”和“港股通”各六个主成分指数，将2012年9月27日至2016年12月31日的股票收盘价数据分为两部分，进一步通过协整检验和协整方程进行分析。

根据本文分析的结果，在“沪港通”开通后，从协整检验的结果分析来看，“沪股通”和“港股通”主成分指数之间的协整个数有所增加，即“沪港通”的开通使两地股市的协整关系有所增强；从协整方程的结果分析来看，“港股通”成分股对于“沪股通”成分股变化的反应逐渐由反向反应略大于正向反应变为正向反应显著大于反向反应，即“沪港通”的开通使两地股市趋于同向变化。

2.建议

（1）从本文的分析结果来看，“沪港通”的开通对两地股市的融合有着显著的促进作用，这对于更好地促进内地股市与国际市场的融合有着重要的启示，我国可以尝试开通更多类似的机制，比如已经开通的“深港通”，将更全面和深入地促进我国股票市场融入到国际市场，更有助于我国金融市场的发展和成熟。

（2）在“十三五”时期，经济发展进入新常态，我国经济将从高速增长转为中高速增长，这说明我国经济发展增速将逐步放缓，但是同时也将更加平稳。这对于开通“沪港通”、“深港通”以及其他可能的类似机制也是一个很好的契机，政府应当把握好发展方向，做好全面的部署，使我国金融市场在这一时期内与国际金融市场稳步对接。

（3）从协整方程估计的结果来看，“沪股通”和“港股通”同向发展的趋势明显，这在股市良性走好的情况下固然是好事，但是也不得不提防金融危机带来的负面作用，应当尽早做好充分的应对准备。两地股市的融合对金融市场有利也有弊，政府应当充分发挥“沪港通”带来的正面作用，对可能的负面影响做好防范措施。

本论文受到上海立信会计金融学院大学生创新创业训练计划资助（项目编号：201611639002）。

[1]谷耀，陆丽娜.沪、深、港股市信息溢出效应与动态相关性——基于DCC-（BV）EGARCH-VAR的检验[J].数量经济技术经济研究，2006（08）.

[2]石建勋，吴平.沪深股市与香港股市一体化趋势的实证研究[J].财经问题研究，2008（09）.

[3]胡坚，吕鹏博.上海股市与香港股市的联动分析[J].山西财经大学学报，2008（12）.

[4]罗子光.香港股市与内地股市的联动性研究[J].南方金融，2008（12）.

[5]丁勇锦.中国内地股市与香港股市联动性研究[D].杭州：浙江大学，2008.

[6]鲁旭，赵迎迎.沪深港股市动态联动性研究——基于三元VAR-GJR-GARCH-DCC的新证据[J].经济评论，2012（01）.

[7]赵彦勇.非参数协整和误差修正模型及其在金融中的应用[D].重庆：重庆理工大学，2013.

[8]张仕洋.我国沪深港股市联动性分析 [J].商业经济研究，2015（01）.

[9]WP PuiHan，HG Fung.Red chips or H shares:which China-backed securities process information the fastest?[J].Journal of Multinational Financial Management，2000（10）.

[10]Mohamed EI Hedi，Fredj J.Nonlinear Stock Market Integration in Emerging Countries[J].International Journal of Economics and Finance，2010（05）.

（作者单位：上海立信会计金融学院）

10.13999/j.cnki.scyj.2017.05.012