一笔画出数学的美——“一笔画”教学实录与评析

◇执教/贠昳琳 评析/张红娜

一 、故事引入，激疑引趣

师：同学们，今天这节课我们要从一个数学故事开始。（结合图1介绍七桥问题，略）

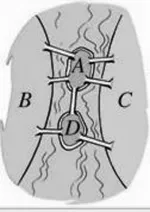
图1

师：你们知道欧拉是用什么方法解决这个问题的吗？又是怎样解决这个难题的吗？

（生答略）

师：欧拉用一笔画的知识解决了这个难题。今天我们就共同研究有趣的一笔画问题。

二、合作探究，发现规律

(一)问题导学。

师：看到一笔画你有什么问题要问？或者你想了解关于它的哪些知识?

生：什么是一笔画？

生：怎么画一笔画？

生：一笔画在生活中有什么用？

……

师：大家提的这些问题都很好。今天这节课我们就来重点研究这几个问题。

（简要板书：是什么？什么规律？有什么用）

（二）新知探学。

1.揭示一笔画的意义。

师：根据你的理解，说一说什么是一笔画。

生：一口气画出来的画，中间不能停顿，不能重复。

师：理解得很好。下笔后笔尖不能离开纸，且每条线只能画一次，不能重复，这样画出来的画就是一笔画了。

2.学生试画一笔画。

师：认识了一笔画，下面我们就来试着画一画。老师先来画一个。（示范画，如图2）

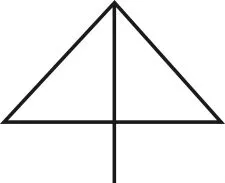
图2

师：你们能不能像老师这样也来画一个？

（要求学生先独立试画，然后选择一个“与众不同”的画在小组的作业纸上。接下来，通过实物投影组织全班同学共同欣赏各小组的作品）

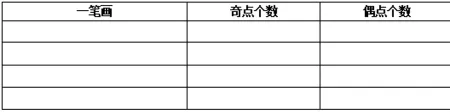
作业纸

3.认识“奇点”和“偶点”。

师:在这张作业纸上，除了让大家在左边画出的一笔画，你还看到了哪些信息？你有什么疑问吗？

生：什么是奇点？什么是偶点？

生：为什么要找奇点个数和偶点个数?

……

师：大家提出的问题真有价值。是啊，我们为什么要统计奇点个数、偶点个数呢？它们跟一笔画有什么联系？对我们学习一笔画的知识有什么帮助？

师：要想解决这些问题，我们先来了解什么是奇点，什么是偶点。如果从一个点引出的线有奇数条，这个点就叫奇点。（如图3）

图3

师：如果从一个点引出的线有偶数条，这个点就叫偶点。（图略）

4.探索并发现一笔画的规律。

师提出问题：同学们知道吗？在一笔画中蕴藏着重要的规律，而这个规律就藏在“奇点个数”或者“偶点个数”中。到底是谁的个数有规律？又是什么规律呢？这个结果是老师告诉你们，还是你们自己来研究？

生：我们自己研究。

师：真好，我特别欣赏大家这种勇于探索数学奥秘的精神！说说看，你们准备怎么研究？

生：先数一数一笔画中奇点和偶点的个数，然后看看谁的数量有规律。

师：从他的发言中，我发现这是一个非常会学习的同学，他解决问题有思路、有办法，真了不起。那我们就按照他的建议先数奇点和偶点的个数吧。咱们先共同来数黑板上这几个图形的奇点个数与偶点个数。

（教师示范数奇点与偶点的个数）

师：这几个图形的奇点个数和偶点个数数出来了，能发现规律吗？

生：不能发现规律，太少了。

师：学习数学，数据越多越有利于我们发现规律。接下来，请每个小组共同统计出你们所画的图形中奇点与偶点的个数。

（学生分小组统计）

师：请每个小组来汇报一下你们数的结果。

（学生边回答，教师边板书）

师：请同学们观察这些数据，你有什么发现？

生：奇点个数有规律。

生：奇点数要么是0，要么是2。

5.运用规律进行判断。

师：不用画，请你利用所学的知识直接判断，图4是一笔画吗?你是怎么知道的？

生：它是一笔画。

生：因为它有2个奇点，其余的都是偶点。符合一笔画的规律。

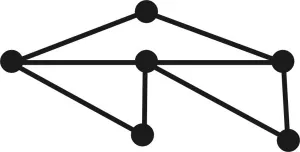
图4

三、联系生活，学以致用

师：一笔画在生活中有着广泛的应用，让我们一起来感受一下。

1.应用一。

师：这是一个游乐场的示意图（如图5），你能沿着一条路线游完每个游乐项目吗？

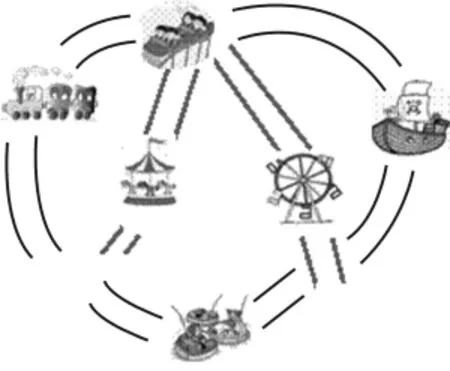
图5

生：能。因为入口和出口这两个点是奇点，其他的都是偶点。

生：这幅图是一笔画，所以能沿一条路线游完每个项目。

师：你准备怎么走？谁来设计一条游玩的路线？

（生在课件上演示不同的路线，略）

2.应用二。

师：有一辆洒水车要给下面的几条街道洒水，司机师傅能先设计出一条路线，然后沿这条路线既不重复也不遗漏地给每条街道洒完水吗？（如图6）

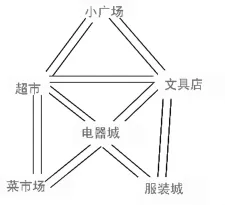
图6

（学生解决问题的过程略）

师小结：利用一笔画的规律，在面对生活中一些问题时，我们可以先做出正确的判断，然后合理灵活地设计解决问题的策略。

四、文化渗透，深刻理解

师：现在让我们回到课前的“七桥问题”。想想看，它和一笔画有什么关系？

师通过课件演示引导：欧拉通过研究认为，能否一次不重复、不遗漏地走完这七座桥，与桥的长短、岛的大小都无关。所以岛和岸都可以看作一个点，而七座桥则可以看作连接这些点的七条线，这样就转化成了一个图形。（如图7）

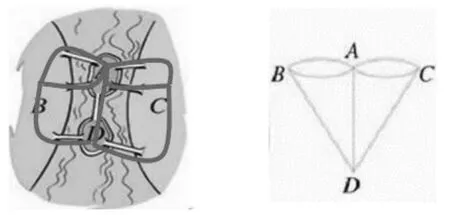
图7

师：你能猜一猜，欧拉是怎么用一笔画的知识来解决“七桥问题”的吗？

生：能否一次不重复、不遗漏地走完这七座桥，要看这个图形是不是一笔画。

生：这个图形中的4个点全是奇点，可以判断它不是一笔画，所以就不能一次不重复、不遗漏地走完这七座桥。

师：你们猜对了！欧拉就是这样判断的，他把“七桥问题”巧妙地转化成了一笔画问题，很智慧地做出了判断，解决了大家公认的难题。让我们一起来认识一下这位伟大的数学家吧。

（课件出示欧拉的照片和简介，略）

五、拓展延伸，提升思维

师：我们再来看“七桥问题”。如果在点B和点C之间再架一座桥，就变成了八座桥（如图8）。那么，一个步行者能不能不重复、不遗漏地一次走完这八座桥？跟“七桥问题”比，它会不会有不同的答案呢？

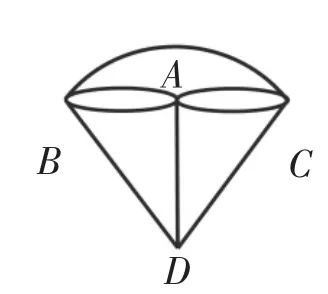
图8

生：能。因为只有A、D两个奇点了，它就变成了一笔画。

师追问：看来，“八桥问题”能解决岛上居民的问题。如果你是这个岛上的居民，你准备从哪儿开始走起？又打算怎么走呢？这是一笔画中又一些值得我们研究的新问题。有兴趣的同学可以带着这些问题课下进行思考、研究。相信大家对一笔画一定会有更深刻的认识！

评析：

本节课通过引导学生“疑中生问”—“探中追问”—“学中解问”—“拓中新问”，较好地培养了学生的问题意识和问题解决能力。

1.疑中生问。

课始，由“七桥问题”引出一笔画后，学生面对新知产生疑问，教师就及时给学生提供发问的机会：“看到一笔画你有什么问题要问？或者你想了解关于它的哪些知识？” “什么是一笔画？”“怎么画一笔画？”“一笔画在生活中有什么用？”……这些问题由学生自然发问，学习活动便在疑问中自然发生。

2.探中追问。

在教学的过程中，教师要引领学生学会“追问”。“奇点”和“偶点”对学生来讲是两个陌生的数学概念，因其数量的多少直接与一笔画蕴含的规律有重要关系，所以，教学时必须让学生知道它们的意义。设计教学时，教师有意把两个概念提前打印在了学生的作业纸上，让学生画一笔画时提前就能看得到，自然就会产生新的疑问：“什么是奇点和偶点？”“为什么要找奇点个数和偶点个数?”“奇点个数和偶点个数与一笔画有什么联系吗？”……这些真实的问题让学习再次发生。在认识“奇点”与“偶点”后，教师告诉学生：“在一笔画中蕴藏着重要的规律，而这个规律就藏在‘奇点个数’或者‘偶点个数’中。”“到底与谁的个数有规律？又是什么规律呢？”学生的疑问再次自然产生，学习也在不断的追问中走向了深刻。

3.学中解问。

发现并提出问题是学习的前提，而分析和解决问题则是学习的最终目的。学生认识了一笔画，知道了它蕴含的规律，这些只是学到的知识。而知识转化成能力，则需要通过具体的问题解决来实现。教学中，教师设计了几个有价值的问题让学生尝试来分析并解决：“你能沿着一条路线游完游乐场的每个游乐项目吗？”“司机师傅能沿着一条路线既不重复也不遗漏地给每条街道洒完水吗？”“欧拉是怎么用‘一笔画’的知识来解决‘七桥问题’的？”“‘八桥问题’跟‘七桥问题’比，会不会有不同的答案呢？”随着这些问题的逐一解决，学生的能力也在一步步地得到提升。

4.拓中新问。

一笔画中涵盖的知识点有许多，本节课只是对它初步的认识。所以，在课的结尾，教师有意进行拓展：“看来，‘八桥问题’能解决岛上居民的问题。如果你是这个岛上的居民，你准备从哪儿开始走起？又打算怎么走呢？”这两个问题涉及一笔画中“起点如何选择”的问题。本节课的教学虽然结束了，但对一笔画的探索并没有结束。我们相信，新的问题会让学生产生新的思考……