浅析MATLAB环境下分形图形的生成

马洪强

引言

19世纪末20世纪初，研究者在探究一些特殊曲线性质时，发现了处处连续但处处不可微曲线，1904年Koch根据这种性质构造出了Koch曲线，该曲线是分形理论初期的研究成果之一。1890年，意大利数学家皮亚诺（Peano G）发现了能填满一个正方形皮亚诺曲线。20世纪学者对分形理论进行了深入研究，Besicovitch等人研究了曲线的维数、分形集的结构、分形集的局部性质及在数论、测度论等方面的应用，特别是维数理论成果丰富。随着维数理论、投影理论、随机技巧等方法先后建立并趋于成熟[1]，使得分形集合的研究形成了自己的方法体系，这一时期分形理论初见雏形。1915年波兰著名数学家希尔宾斯基（Sierpinski）提出了Sierpinski 三角形及Sierpinski 地毯[2]，1919年法国数学家嘉斯顿·茹利亚（Gaston Julia）研究了迭代保角变换[3]，成为后来人们借助计算机展现一幅幅精彩的图画的理论基础。 20世纪70年代，美籍法裔犹太科学家曼德勃罗（Mandelbrot）在总结前人的基础上发表了《分形：形状、机遇和维数》，第一次系统阐述分形几何的思想、内容、意义和方法，标志着分形几何作为独立学科正式诞生。特别是1980年Mandelbrot借助计算机将Mandelbrot集（M-集）展示在荧屏上，标志着分形艺术初步形成，随着分形软件的开发应用，分形图形以其绚丽多彩的色彩感冲击着人们的视觉感受。现代艺术也渐渐将分形思想应用到创作中，甚至部分艺术家直接创作分形作品进行展览。

2004年2月3日，分形几何之父Gaston Julia诞辰111周年，Google网站logo结合Julia集分形图形做了创新设计，以纪念这位数学家。

本文分四个部分，第一部分介绍了什么是分形；第二部分介绍MATLAB软件.M文件运行步骤；第三部分在MATLAB（Matrix Laboratory）环境下，以Koch曲线为例介绍分形图形的产生过程；第四部分介绍Julia集和M集分形实例的MATLAB程序；第五部分阐述Sierpinski地毯的向量化编程技术及其变异，并将向量化编译程序随机化，拓宽了分形图形生成方法；第六部分对向量式随机分形程序的意义和不足做了说明，并阐述了随机分形意义所在。

一、 分形

1.1 分形定义

迄今为止，分形还没有严格意义上的定义。1982年，曼德勃罗定义“Hausdorff维数严格大于拓扑维数的几何称为分形”，四年后又提出“组成部分以某种方式与整体相似的形体叫分形”，但依然不够确切和严格。现阶段多数引用法尔内克（K.Falconer）对分形集合F的描述：

1）F具有精细的结构，即在任意小的尺度之下，它总有复杂的细节；

2）F是不规则的，以至它的整体和局部不能用传统的几何语言来描述；

3）F通常具有某种自相似性，这种自相似性可以是统计意义上的，也可以是近似的；

4）F在某种意义下的分形维数通常都大于它的拓扑维数；

5）在多数情况下，F以非常简单的方法定义，或以递归或迭代过程产生。

1.2 分形图形分类

分形可以分为规则分形和不规则分形。一些数学家提出过不少复杂和不光滑的集合，例如Cantor集、Koch曲线、Sierpinski三角、地毯和海绵等，都属于规则分形，它们具有严格的自相似性。但自然界许多事物的不光滑性和复杂性往往是随机的，像蜿蜒曲折的海岸线，随机布朗运动等，这类曲线的自相似性是近似的或统计意义上的。

下面以Koch曲线为例，阐述Matlab环境下，分形图形的生成过程。

二、 Matlab软件介绍

MATLAB软件是美国Mathworks公司开发的一款优秀的数学软件，MATLAB是Matrix Laboratory(矩阵实验室)的组合缩写。该款软件将数据分析、矩阵计算可视化，并集成了非线性动态系统的仿真。MATLAB软件不仅适用于学术研究，还在模拟仿真等现实工作中得到应用，其版本以其应用广泛，不断得到更新，目前已更新到MATLAB 15.0版本。本文以经典版本MATLAB 7.0为例，简单介绍在分形应用时MATLAB软件应用步骤。

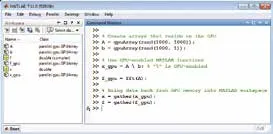
MATLAB软件界面主要包含工具栏、命令窗口(Command Windows)、命令历史窗口(Command History)、工作间管理窗口（Workspace）、当前路径窗口(Current Directory)、编译窗口、图形窗口等。

运行分形.M文件有多种方式，本文简单介绍打开.M文件运行方式。在Matlab界面中选择工具栏文件菜单中打开选项，按存储路径选中.M文件，打开.M文件后单击运行按钮即可得到分形图。

使用.M文件运行程序比较简单直接，便于保存、修改设计程序。[4]

三、 Matlab环境下的Koch曲线分形实现

本文以科赫曲线为例，在阐述分形的数学思想基础上来详细说明分形原理及在Matlab环境下分形图形的实现过程。

Koch曲线的构造是将单位为1的一条线段变成四条，且每条线段为1/3，因此变换n次后的Koch曲线总长度为（4/3）^n，当n→∞，则Koch曲线趋于无穷大，Koch曲线的分形维数：D=ln4/ln3=1.2618。

Koch曲线的递归过程如图3.1所示：

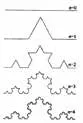
图3 .1

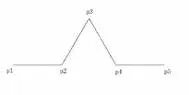
图3 .2

3.1 算法分析

如图3.2所示，考虑由直线段（2个点）产生第一个图形（5个点）的过程。图中，设p1和p2分别为原始直线段的两个端点，现需要在直线段的中间依次插入三个点P2，P3，P4；P2，P4分别位于线段三分之一处，线段三分之二处，P3点的位置可看成是由点P4以点P2为轴心，逆时针旋转60°而得。旋转由正交矩阵实现。

根据初始数据（P1和P5点的坐标），产生图中5个结点的坐标。结点的坐标数组形成一个矩阵，矩阵的第一行为P1的坐标，第二行为P2的坐标……，第五行为P5的坐标。矩阵的第一列元素分别为5个结点的x坐标，第二列元素分别为5个结点的y坐标。

进一步考虑Koch曲线形成过程中结点数目的变化规律。设第k次迭代产生的结点数为n(k)，第k+1次迭代产生的结点数为n(k+1)，则n(k)和n(k+1)中间的递推关系为n(k+1)=4n(k)-3。

3.2 Matlab程序实现

p=[0 0;10 0]; %P为初始两个点的坐标，第一列为x 坐标，第二列为y坐标

n=2; %n为结点数

A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %旋转矩阵

for k=1:9

d=diff(p)/3; %diff计算相邻两个点的坐标之差， 得到相邻两点确定的向量%则d就计算出每个向量长度的三分之一，与题中将线段三等分对应

m=4*n-3; %迭代公式

q=p(1:n-1，:); %以原点为起点，前n-1个点的坐标为终点形成向量

p(5:4:m，:)=p(2:n，:); %迭代后处于4k+1位置上的点的坐标为迭代前的相应坐标

p(2:4:m，:)=q+d; %用向量方法计算迭代后处于4k+2位置上的点的坐标

p(3:4:m，:)=q+d+d*A′; %用向量方法计算迭代后处于4k+3位置上的点的坐标

p(4:4:m，:)=q+2*d; %用向量方法计算迭代后处于4k位置上的点的坐标

n=m; %迭代后新的结点数目

end

plot(p(:，1)，p(:，2)) %绘出每相邻两个点的连线

axis([0 10 0 6]) %设置坐标显示

3.3 Matlab程序运行结果

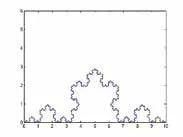
Koch曲线Matlab示例见参考文献[5]。

四、 Julia集和M-集分形MATLAB程序

Julia集和M-集分形MATLAB程序设计有很多种方法，为便于艺术工作者应用MATLAB程序实现分形，此处介绍了较方便的程序设计，在程序运行时间上也较省时。

4.1 Julia集MATLAB程序

a=-0.13;b=0.77;r=2;

for x0=-1:0.01:1

for y0=-1:0.01:1

x=x0;y=y0;

if x0^2+y0^2＜1

for n=1:80

x1=x*x-y*y+a;

y1=2*x*y+b;

x=x1;

y=y1;

end

if (x*x+y*y)＜r

plot(x0，y0);

end

hold on;

end

end

end

4.2 M-集 MATLA程序

r=1; %限界值

for a=-1:0.002:1

for b=-1:0.002:1 %参数a，b取到一个范围

x=a;y=b; %初始的复数c

for n=1:20

x1=x*x-y*y+a; %复数平方加一个c的运算

y1=2*x*y+b;

x=x1; %迭代

y=y1;

end

if(x*x+y*y)＜r %限界

plot(a，b);

end

hold on;

end

end

五、 Sierpinski地毯

5.1 矩阵法 Sierpinski地毯

图5 .1.1

Sierpinski地毯是具有代表性的经典分形，可有迭代算法产生。将一个正方形n^2个相等的边长为1/n的小正方形，依据一定规则挖去k^2个小正方形，得到Sierpinski地毯的生成元，重复上述过程就可得到Sierpinski地毯。

利用MATLAB的imagesc函数，将正方形用矩阵中的方阵模拟，构造迭代矩阵，对方阵进行填充，绘制Sierpinski地毯分形图，具体程序如下：

function M=Sierpinski(i)

tic

M=0

for j=1:i

M=[M， M， M;

M， ones(3^(j-1))*1， M;

M， M， M];

end

imagesc(M);

colormap(spring);

axis equal;

axis off;

toc

将上述程序保存为Sierpinski.m文件，在MATLAB的command Window中输入M=Sierpinski(4)得到图形5.1.1此例详见参考文献。[6]

在构造迭代矩阵时，将迭代矩阵构造成不完全对称矩阵，就得到变异Sierpinski地毯分形图，如图5.1.2所示，程序如下：

function M=Sierpinski(i)

tic

M=0

图5 .1.2

for j=1:i

M=[ones(3^(j-1))*9， M， M;

M， M， M;

M， M， ones(3^(j-1))*9];

end

imagesc(M);

colormap(autumn);

axis equal;

axis off;

toc

虽然利用imagesc函数，通过构造迭代矩阵的方法简单明了，便于计算，更易通过改变矩阵形式，产生新的分形图。但在实际运行过程中，受到一定因素的限制，只能进行有限的迭代，对于提高分形图形的精度及细腻程度存在不足。该方法仅为一般状态下的规则分形，没有考虑随机因素，因此图形呈现比较单一。

5.2 Sierpinski地毯向量式随机程序生成分形图

基于3.1Sierpinski地毯变异程序基础上，添加随机因素，使其影响分形生成结果，从而使得分形图形产生变化。本例应用matlab中rand函数产生随机数，并依概率采用有差别化向量法程序，程序如下

function M=SS (i)

tic

M=0

for j=1:i

r=rand

if r＜0.5;

N=M;

M=[ones(3^(j-1))*9， M， N;

M， N， M;

N， M， ones(3^(j-1))*9];

else，

N=ones(3^(j-1))*9;

M=[ones(3^(j-1))*9， M， N;

M， N， M;

N， M， ones(3^(j-1))*9];

end

end

imagesc(M);

colormap(autumn);

axis equal;

axis off;

toc

将程序存储为SS.m函数，在command window中输入M=SS(4)将得到不同图形，本例给出部分分形结果，如图5.2所示:

图5 .2

六、 展望

虽然向量式随机分形程序设计解决了向量式随机分形程序的随机问题，但是受制于矩阵法缺陷，有限迭代问题没有解决。此外，对于程序设计等也值得研究，以便得到改进，缩短运行时间。因此也为此类方法的前景及研究提出了新的问题。

从应用领域来说，向量式随机分形程序设计方法使得分形结果产生随机变化，为分形图形的不确定性提供了可能，并使MATLAB环境下分形图形与艺术设计领域相关学科相互交叉，从而在分形艺术应用方面提供了可能；同时，艺术设计的发展需求也对分形提取更高要求。