微电网三相负荷不平衡的量子遗传优化算法研究

程启明, 黄 山, 张 强, 褚思远, 杨小龙

(上海电力学院 自动化工程学院，上海 200090)

微电网三相负荷不平衡的量子遗传优化算法研究

程启明, 黄 山, 张 强, 褚思远, 杨小龙

(上海电力学院 自动化工程学院，上海 200090)

为了解决微电网中普遍存在的三相负荷不平衡问题，详细分析了微电网三相负荷不平衡特征，提出了一种新的微电网三相负荷计算方法，并采用了改进型量子遗传算法对模型进行优化求解。所用的量子优化算法中引入了双链式结构和动态旋转角调整策略，提出了一种新的改进型量子遗传算法，并求解得出合适的解，从而获得最优的三相负荷接入方案。最后通过算例仿真验证了所提模型、策略和算法的有效性和可行性。

微电网; 三相负荷不平衡; 量子遗传算法; 双链结构; 动态旋转角调整; 优化运行

0 引 言

近些年来在电改的大背景下，微电网能量优化管理越来越受到重视，微电网三相负荷不平衡一直是影响微电网电能质量的问题之一[1]。现在大多数的微电网是先经10 kV/400 V的降压变后再向用户供电，接线方式为三相四线制居多，少数为三相三线制。当地供电局在安接单相负荷时基本将负荷平均分配在A、B、C三相上，但在实际工作及运行中，用户用电量的短时间猛增以及大功率用电设备的持续运行，迫使配电侧的三相负荷不平衡问题日益严重。微电网三相负荷不对称是导致微电网出现三相负荷不平衡的主要原因，尤其是在微电网低压台区，低压配电线路不合理、单相接入负荷不可控、单相负荷不同时性以及三相负荷性质不同等因素，使得微电网三相负荷不平衡问题日益突出[2-4]。

目前对于微电网三相负荷不平衡问题，国内外学者都做过积极探索。文献[5]考虑了配电网的三相负荷不平衡问题，给出了配电网三相负荷不平衡模型，并采用了粒子群(Particle Swarm Optimization，PSO)算法求解，但PSO算法存在早熟等问题。文献[6]仅对配电网出现三相负荷不平衡的原因和常规解决方法进行了分析，并未举出案例和提出实际方案。文献[7]建立了微电网负荷优化分配模型，运用PSO算法对模型求解，模型的构建仍处于优化调度范畴，对三相负荷不平衡尚未考虑。文献[8]对于配电网三相负荷不平衡调整进行了讨论，以某供电所为例讨论了不平衡原因及调整方案，但其策略尚不智能，数据需为2天前所得，不能实时参考。

上述这些国内文献尚未对微电网中的三相负荷不平衡问题进行研究，且对于具体电网的网络构架考虑不够全面具体，电能质量问题考虑不够充分，有些解决方案存在经济成本较高等问题。此外，采用的PSO优化算法存在早熟、容易陷入局部最优、鲁棒性差等问题。

为了解决上面优化方法问题，本文引入了量子遗传算法(Quantum Genetic Algorithm，QGA)[9-11]，QGA是基于量子计算原理的一种遗传算法(Genetic Algorithm，GA)。其将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，实现了比常规GA或PSO更好的效果。但基本QGA算法存在编码随机性和频繁解码问题，因此，本文提出了一种双链式结构进行改进的方法，即采用动态调整旋转角调整策略和自适应的调整算法搜索角度。

在上述研究背景下，本文以三相负荷不平衡度和经济效益指标，建立微电网三相负荷不平衡模型，以选择用户的相序接入顺序为解决方案，引入了双链式结构和动态旋转角调整策略，提出一种改进型量子遗传算法(Improved Quantum Genetic Algorithm，IQGA)对微电网模型优化求解，得出最优的相序调整方案。最后通过仿真试验验证了所提模型、策略和算法的有效性。

1 微电网三相负荷不平衡数学模型

1. 1 微电网三相负荷不平衡

21世纪我国配电线路的接线方式大多为三相四线制，变压器的接线方式为Y/Y0，在380 V的线路中超过85%的负荷为单相负荷，此外单相负荷运行时间不一样，以及装接表考虑不全等原因，致使微电网三相负荷不平衡的现象广为存在。微电网的负荷多存在随机性和动态性，所以有序的接入单相负荷，降低微电网三相负荷不平衡度显得尤为重要。

(1) 微电网三相负荷不平衡优化模型。微电网用户共有N个，微电网用户接入相序可用如下矩阵表示：

(1)

式中：mxi∈(0，1)，其中，x=A、B、C,i=1、2、3…N。mxi=0、1时分别表示第i个负荷不接入、接入第x相序。

一般情况下微电网内居民用户负荷以单相负荷为主，则mAi+mBi+mCi=1。设用户的换相成本为H=[h1h2…hN]，用户表号为J=[j1j2…jN]，用户负荷为P=[p1p2…pN]。设G(mAi,mBi,mCi)表示用户i是否换相，G∈(0，1)，当G=0时表示用户不换相，当G=1时表示用户换相。

本文采用常规的微电网日内负荷模型，以三相负荷不平衡最低的情况下，经济成本最小为目标，建立的数学模型为

(2)

(3)

三相负荷不平衡度数学模型为

(4)

(2) 微电网三相负荷不平衡度分析。假设某微电网在一段时间T内，对用户负荷进行分相x，x(A,B,C)，用电负荷为Px，相平均电压为Ux，功率因数为cosθ，则平均分相电流Ix计算方法为[5]

(5)

设A、B、C三相的平均负荷电流为IAav、IBav、ICav，中性线平均负荷电流为Inav，这里用中性线平均负荷电流和三相负荷总电流的比值表示三相不平衡程度，其计算公式为

(6)

三相负荷电流和零线负荷电流的矢量关系为Inav=IAav+IBav+ICav，根据电力系统中正序、负序和零序之间的关系可得

(7)

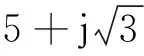
则Inav的幅值为

(8)

有中性线的配电线路电压波动变换较小，但是电流会出现不平衡的情况。简化分析，A、B、C三相平均电压大致相等，功率因数可近似为1，通过上述公式计算可得

(9)

1. 2 微电网三相负荷函数建立

微电网三相负荷平均值为

(10)

式中：PAi、PBi、PCi——微电网A、B、C三相中第i个负荷；

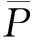
微电网三相负荷函数PABC为

(11)

式中：nA、nB、nC——A、B、C中的所有负荷。

2 IQGA算法

2. 1 基本的QGA算法

QGA建立在量子的态矢量表示的基础之上，将量子比特的几率幅表示应用于染色体的编码，使得一条染色体可以表达多个态的叠加，并利用量子逻辑门实现染色体的更新操作，从而实现目标的优化求解。

(1) 量子比特编码。在量子计算机中，充当信息存储单元的物理介质是一个双态量子系统，称为量子比特。量子比特与经典位不同就在于它可以同时处在两个量子态的叠加态中：

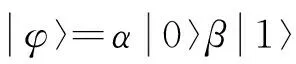
(12)

(13)

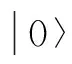
α、β——两个幅常数。

在QGA中，采用量子比特存储和表达一个基因。该基因可以为“0”态或“1”态，或其任意叠加态，即该基因所表达的不再是某一确定的信息，而是包含所有可能的信息，对该基因的任一操作也会同时作用于所有可能的信息。

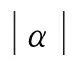
(2) 量子门更新。量子门作为演化操作的执行机构，可根据具体问题进行选择。目前已有的量子门有很多种，根据QGA的特点，选择量子旋转门较为合适。量子旋转门的调整操作为

(14)

其更新过程如下：

(15)

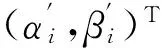
θi——旋转角，其大小和符号由事先设计的调整策略得出[9]。

2. 2 IQGA

本文基于典型GA和基本QGA[9-11]，提出了一种IQGA。 IQGA改进之处主要有：采用了一种双链式结构，克服编码存在的随机性及基础QGA在优化求解过程中存在的频繁解码的问题，并采用动态调整旋转角调整策略和自适应的调整算法搜索角度。

(1) 双链式结构操作。采用GA中的二进制编码，对存在多态的问题进行量子比特编码，采用4态用2个量子比特进行编码。采用多量子比特编码m个参数的基因如下：

(16)

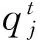
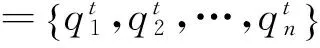
(17)

式中：tij=2πζ；ξ——(0,1)间的随机数；i=1,2,…,n；j=1,2,…,m。

每条染色体包含两个并列的基因链，每条基因链可代表一个优化解。因此，每条染色体代表搜索空间中的两个最优解：

(18)

(19)

式中：Pic——“余弦”解；Pis——“正弦”解。

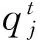
s(αi,βi)动态旋转角的选择策略如表1所示。表中，xi为当前染色体的第i位；besti为当前的最优染色体的第i位；f(x)为适应度函数；s(αi,βi)为旋转角方向；Δθi为旋转角度大小，其值由表1中所列的选择策略确定。

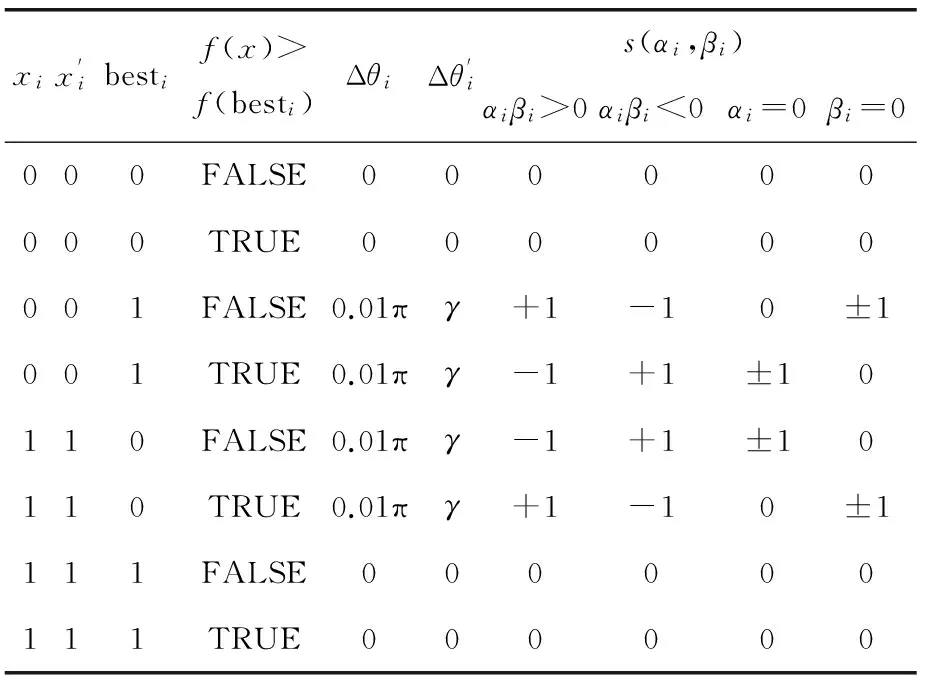
表1 动态旋转角选择策略

表1中γ的表达式为

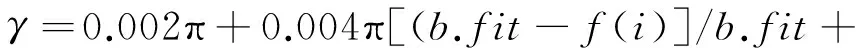
(20)

式中：b.fit——最优适应度值；fit(i)——当前适应度值；Mgen——最大进化代数；gen——当前进化代数。

2. 3 IQGA流程

图1为IQGA原理流程图。IQGA的具体过程描述如下：

(1) 初始化种群Q(t0)，随机生成多个以量子比特为编码的染色体；

(2) 对初始种群Q(t0)中的每个个体进行一次测量，得到对应的确定解P(t0)；

(3) 对各确定解进行适应度评估；

(4) 记录最优个体和对应的适应度；

(5) 判断计算过程是否可以结束，若满足结束条件则退出，否则继续计算；

(6) 判断是否采用新的量子门旋转角度，若不采用则继续计算,若采用则跳转到步骤(12)；

(7) 对种群Q(t)中的每个个体实施一次测量，得到相应的确定解；

(8) 对各确定解进行适应度评估；

(9) 利用量子旋转门U(t)对个体实施调整，得到新的种群Q(t+1)；

(10) 记录最优个体和对应的适应度；

(11) 将迭代次数t加1，返回步骤(5)；

(12) 计算新的量子门旋转角度；

(13) 对种群Q(t)中的每个个体实施一次测量，得到相应的确定解；

(14) 对各确定解进行适应度评估；

(15) 利用量子旋转门U(t)对个体实施调整，得到新的种群Q(t+1)；

(16) 记录最优个体和对应的适应度；

(17) 将迭代次数t加1，返回步骤(5)。

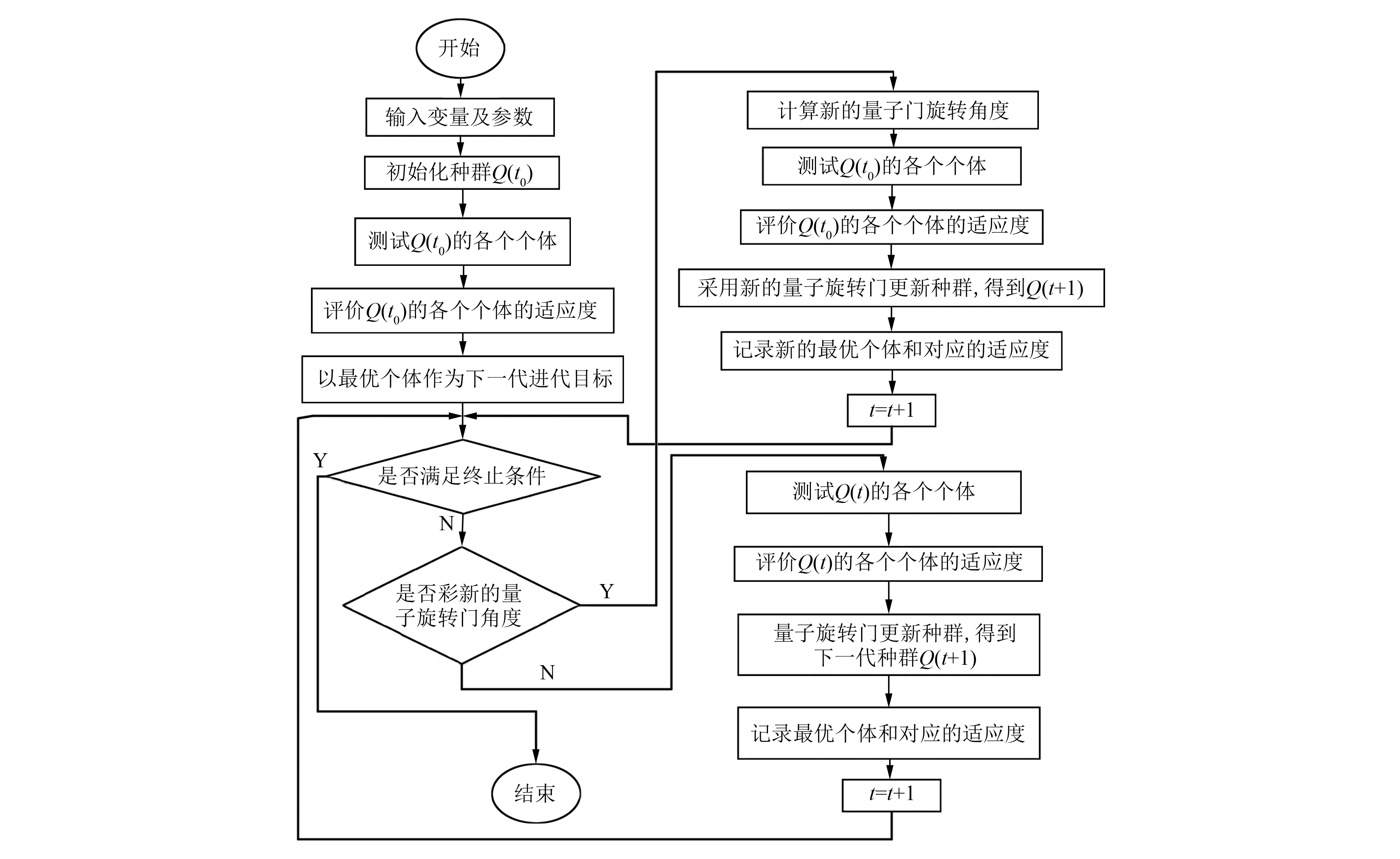
图1 IQGA流程图

3 算例分析

本文的算例采用微电网台区拓扑结构如图2所示。图2中，假设微电网用户负荷分为3个小区，且每个小区有3个主要负荷。微电网台区接线方式采用三相四线制与单相两线制组合接线方式。

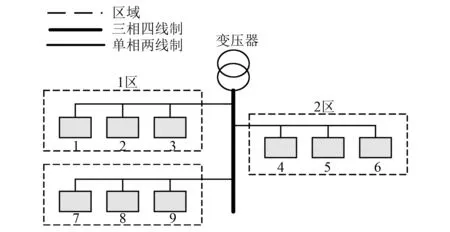
图2 微电网三相负荷拓扑图

3. 1 算例1

此时微电网内各相用户的月用电量如表2所示；微电网居民社区电气结构如图3所示。表2中的数据加上(前)表示未经优化时的负荷相序情况。根据表2中的数据可计算出式(9)的微电网三相负荷不平衡度=8.821%。由此可知，微电网的三相负荷不平衡度较为严重。

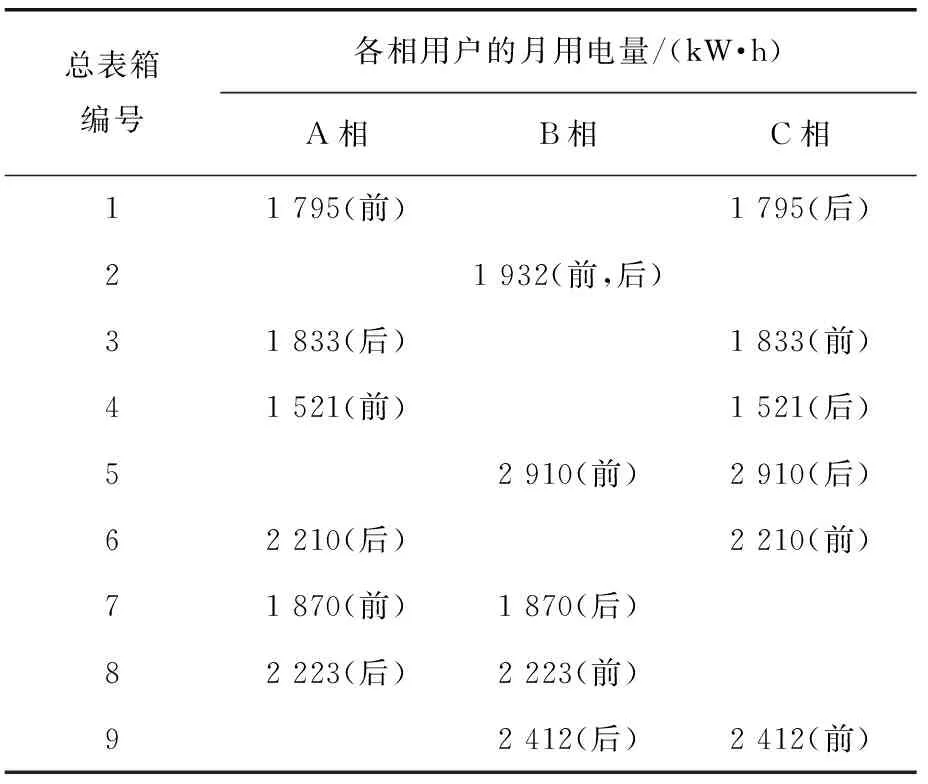
表2 调整前后微电网各相用户的月用电量

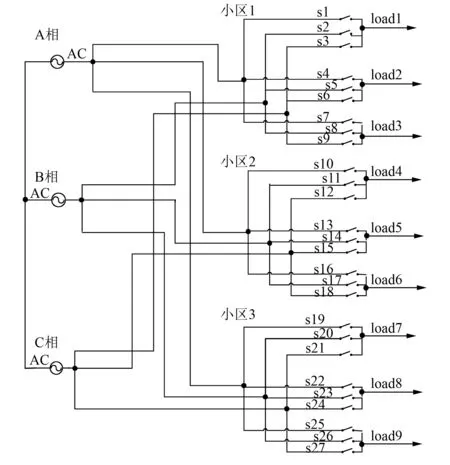
图3 微电网居民社区电气结构图

运用IQGA对微电网三相负荷不平衡模型进行求解。算法参数设置如下：IQGA的种群规模为100，最大遗传代数为200，每个变量的二进制长度为20，从而获得最优的三相负荷接入方案。经过计算后出新的相序方案,如表1所示。表2中的数据加上(后)表示经过本文所提优化后的负荷相序变化情况。

由表2可见，1号总表箱用户从A相调整到C相；3号总表箱用户的相序从C相调整到A相；4号总表箱用户从A相调整到C相；5号总表箱用户从B相调整到C相；6号总表箱用户的相序从C相调整到A相；7号总表箱用户的相序从A相调整到B相；8号总表箱用户的相序从B相调整到A相；9号总表箱用户的相序从C相调整到B相。

3. 2 算例2

此时微电网内用户负荷如表3所示。由此可计算出三相负荷不平衡度=4.395%，可见此时配变台区的三相负荷不平衡度较严重。

此时算法参数设置如下：IQGA种的群规模为100，最大遗传代数为200，每个变量的二进制长度为20。

经过优化计算后的新的相序方案见表3。由表3可见，1号总表箱用户从A相调整到B相；2号总表箱用户从B相调整到A相；3号总表箱用户的相序没有调整；4号总表箱用户从A相调整到B相；5号总表箱用户的相序没有调整；6号总表箱用户的相序从C相调整到A相；7号总表箱用户的相序从A相调整到B相；8号总表箱用户的相序从B相调整到A相；9号总表箱用户的相序从C相调整到B相；10号总表箱用户的相序没有调整；11号总表箱用户从B相调整到C相；12号总表箱用户从A相调整到B相；13号总表箱用户的相序没有调整；14号总表箱用户的相序从C相调整到A相；15号总表箱用户从B相调整到C相；16号总表箱用户从A相调整到C相；17号总表箱用户从B相调整到C相；18号总表箱用户的相序从C相调整到A相；19号总表箱用户的相序没有调整；20号总表箱用户从B相调整到C相；21号总表箱用户的相序没有调整；22号总表箱用户从A相调整到C相。

表3 调整前后微电网各相用户的月用电量

4 结 语

本文构建了微电网三相负荷不平衡模型，提出了一种计算微电网三相负荷新方法以及解决微网三相负荷不平衡的优化调度策略。在考虑平衡约束和不平衡约束的条件下，提出了采用IQGA对微电网三相负荷不平衡模型进行求解，得出一套相序调整方案，经过仿真验证了所提模型、策略和算法的有效性和可行性。本文所提的负荷调整方案对微电网三相负荷不平衡度的降低、线路损耗的减小、配电变压器损耗的减少、配变出力的合理分配以及用电设备安全运行效率的提高等方面都具有参考指导价值。

[1] 林海雪.电力系统的三相不平衡[M].北京: 中国电力出版社,1998.

[2] 米勒TJE.电力系统无功功率控制[M].胡国根，译.北京: 水利电力出版社,1990.

[3] 鲁中相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化,2007,31(19): 100-107．

[4] 王成山,肖朝霞,王守相.微网综合控制与分析[J].电力系统自动化,2008,32(7): 98-103.

[5] 张明,谢珊珊,罗云峰.低压配电网三相负荷不平衡优化模型的研究[J].武汉科技大学学报,2015,38(1): 59-63.

[6] 吴联梓,王磊,司远.浅谈低压配电网三相负荷不平衡问题[J].科技与展望,2014,12(23): 80-81.

[7] 陈达威,朱桂萍.微电网负荷优化分配[J].电力系统自动化,2010,10(20): 45-50.

[8] 侯剑波,乔晓东.配电网运行监测系统对三相负荷不平衡调整的探讨[J].农村电气化,2015,7(9): 20-22.

[9] 沙林秀,贺昱曜,陈延伟.一种变步长双链量子遗传算法[J].计算机工程与应用,2012,48(20): 59-63.

[10] 周建平,林韩,温步瀛,等.改进量子遗传算法在输电网规划中的应用[J].电力系统保护与控制,2012,40(19): 90-96.

[11] 刑焕来,潘炜,邹喜华,等.一种解决组合优化问题的改进型量子遗传算法[J].电子学报,2007,35(10): 1999-2004.

欢迎投稿 欢迎订阅 欢迎刊登广告

Study on Quantum Genetic Optimal Algorithm of Three Phase Unbalanced Load in Microgrid

CHENGQiming,HUANGShan,ZHANGQiang,ZHUSiyuan,YANGXiaolong

(College of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

In order to solve microgrid ubiquitous three-phase load imbalance, a detailed analysis of the microgrid three-phase unbalanced load characteristics, a new method for the calculation of three-phase load microgrid was proposed, and used an improved quantum genetic algorithm the model optimization solution. Quantum optimization algorithms used in the introduction of double chain structure and dynamics of the rotation angle adjustment strategy proposes a new improved quantum genetic algorithm, obtained the right solution and solve to obtain access to the best three-phase load program. Finally, an example demonstrated the effectiveness and feasibility of the proposed model, strategies and algorithms.

microgrid; three-phase unbalanced load; quantum genetic algorithm; double-stranded structure; dynamic rotation angle adjustment; optimal operation

国家自然科学基金(61304134)；上海市重点科技攻关计划(14110500700)；上海市电站自动化技术重点实验室(13DZ2273800)

程启明(1965—)，男，教授，硕士生导师，研究方向为电力系统自动化、发电过程控制、先进控制及应用等。 黄 山(1992—)，男，硕士研究生，研究方向为电力系统自动化、微电网优化与运行等。 张 强(1989—)，男，硕士研究生，研究方向为电力系统自动化、电力系统自动化、微电网优化与运行等。 褚思远(1990—)，男，硕士研究生，研究方向为电力系统自动化、电力系统自动化、微电网测量与控制等。 杨小龙(1988—)，男，硕士研究生，研究方向为电力系统自动化、电力系统自动化、微电网测量与控制等。

TM 734

A

1673-6540(2017)05- 0056- 07

2016 -10 -25