基于新型变速趋近律的永磁同步电机滑模控制
李中琴
(新乡学院 机电工程学院,河南 新乡 453003)
基于新型变速趋近律的永磁同步电机滑模控制
李中琴
(新乡学院 机电工程学院,河南 新乡 453003)
为了改善永磁同步电机(PMSM)调速系统的动态品质,提出了一种基于变速趋近律方法的PMSM滑模速度控制策略。为了提高传统指数趋近律的收敛速度和消除系统抖阵现象的影响,在传统指数趋近律的基础上提出了一种新型变速趋近律方法,并应用该方法设计了一种PMSM调速系统的滑模速度控制器。通过仿真和试验结果对比分析,证明该算法不仅改善了系统的鲁棒性能,同时改善了系统的动态响应速度。
永磁同步电机; PI控制; 变速趋近律; 滑模控制
0 引 言
目前,蓄电池电机车仍然是全国各煤矿使用的主要运输设备,且驱动装置多采用直流电机。但直流电机存在电刷损害率高、维护成本高等缺点,已成为制约煤矿现代化的重要因素。永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)由于具有结构简单、体积小、效率高和功率密度高等诸多优点,被广泛用于电力机车、空调压缩机及其他通用机电设备[1-2]。但是,PMSM是一个典型的复杂非线性系统,当速度控制器采用传统的PI控制式,虽然在一定程度上能满足控制性能的需要,当电机长时间运行或受到外界扰动的影响时,电机的参数都会发生一定的变化,传统的PI控制并不能获得较好的控制性能。
为了进一步提高PMSM调速系统的控制性能,随着现代控制技术的不断发展,一些先进的控制算法逐步被应用于矿用PMSM调速系统。特别是滑模控制作为一类特殊的非线性控制,由于其鲁棒性强和动态响应速度快等诸多优点,在一定程度上得到了广泛应用[3-6]。目前,滑模控制器的设计普遍采用指数趋近律方法,虽具有良好的控制性能,但对于一个指定的系统而言,指数趋近律的参数一般都是固定的,并不具有自调节功能。为了解决上述问题,本文首先设计了一种系统的状态变量可根据距离平衡点的远近而自适应调节参数的变速指数趋近律方法,并将此方法应用到PMSM调速系统的设计。最后仿真和试验结果验证了该算法的可行性和有效性,提高了系统的动态品质。
1 PMSM的数学模型
建立dq坐标系下表贴式PMSM的数学模型为[7-8]
(1)
式中:ud、uq、id、iq——定子电压和电流;Ls、R——定子电感和电阻;p——电机的极对数;ψf——永磁体的磁链;ω——机械角速度;TL——负载转矩;J——转动惯量。
当采用控制策略id=0时,表贴式PMSM矢量控制具有较好的控制效果。此时式(1)则可变为如下的数学模型:
(2)
定义系统的状态变量:
(3)
式中:ωref——电机的参考转速,并假定ωref存在二阶导数。
根据式(2)和式(3)可知:
(4)
由于电机在实际运行过程中会出现电机参数的变化。此时,式(4)可表示为
(5)
式中: Δa、Δb、Δc——对应项的参数不确定项。
假设g(t)为系统总的不确定项,表达式为
(6)
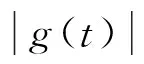
将式(6)和式(5)代入式(3),可得系统的数学模型:
(7)

2 基于趋近律方法的滑模控制器设计
2. 1 新型趋近律方法
目前,常用的指数趋近律方法为

(8)
在指数趋近律方法中,为保证快速趋近的同时削弱抖振,应在增大μ值的同时减小k值。该方法虽然可以通过减小k、增大μ加速趋近过程,并大大削弱了抖振,但等速项ksgn(s)的存在使系统并不能从理论上消除抖振。
为了进一步提高趋近律的趋近速度,本文提出一种变指数趋近律方法,即:
(9)

为了说明文中所提趋近律方法的优越性,在使用相同参数的条件下,得到了如图1所示的仿真结果。从图1可看出,系统的状态变量从初始值到达平衡点的过程中,相比其他两种算法,文中提出趋近律方法的收敛速度具有明显的优势,且系统的抖振现象也得到了抑制。

图1 两种趋近律方法的性能比较
2. 2 滑模变结构速度控制器设计
定义滑模面函数为
(10)
式中:c——设计参数,c>0。
对于滑模控制器,通常包括等效控制ueq和切换控制uvs,即
(11)
求解等效控制ueq,忽略总的不确定量的影响,令g(t)=0即可求得。切换控制uvs的主要作用就是抵消外界扰动的影响。采用文中的新型趋近律方法,即可得到滑模控制器的表达式,即
(12)
为了证明系统的稳定性,定义Lyapunov函数为
(13)
对Lyapunov函数求导,并将控制器代入,可得
(14)
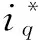
(15)
从式(15)可以看出,由于积分器的作用,一方面调高了系统的收敛速度,另一方面削弱了系统的抖振现象。
3 仿真和试验结果分析
采用如图2所示的PMSM矢量控制技术验证上述控制算法的可行性和有效性。其中,速度控制器采用上述滑模控制;dq轴的电流控制器采用传统的PI控制。

图2 PMSM调速系统控制框图
3. 1 仿真结果分析
在MATLAB/Simulink环境下搭建系统的仿真模型,电机参数设置如下:定子电阻为R=2.46 Ω,定子电感Ls=6.35 mH,永磁体磁链ψf=0.175 Wb,转动惯量J=1.02 kg·m2,摩擦因数B=0.000 1 N·m·s,极对数p=4。
为了便于比较分析,图3和图4分别给出了突加负载条件时PI控制和文中所提滑模控制作用下的仿真结果,仿真条件转速值设定为500 r/min。从图3、图4可以发现,在PI控制作用下能够进入稳态状态,且电机转速有超调;在文中所提控制算法作用下能够在更短的调节时间内进入稳态状态,且电机转速无超调。可见,相比PI控制,文中所提控制算法具有较快的动态性能。

图3 基于PI速度控制器的仿真结果

图5 基于PI速度控制器的试验结果
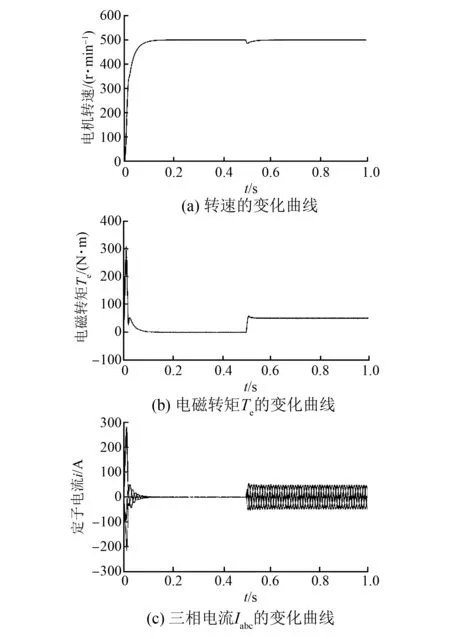
图4 基于滑模速度控制器的仿真结果图
3. 2 试验结果分析
为了进一步验证算法的可行性和有效性,图5和图6分别给出了同样采用图2所示的控制框图的试验结果,其中参考转速与仿真中的参数设定相同,并且是系统稳态运行后突加负载时的变化曲线。其中,图5(a)和图6(a)分别为两种控制策略下转速的变化曲线,而转矩的变化曲线如图5(b)和图6(b)所示。

图6 基于滑模速度控制器的试验结果
从以上试验结果可发现,相比采用PI速度控制器时,采用文中所提滑模速度控制策略时,系统转速、转矩具有较好的动态响应速度,且转速波动小,抗外界扰动能力强,从而验证了算法的可行性和有效性。
4 结 语
为了提高PMSM调速系统的动态调速性能,本文首先给出了包含参数不确定性的数学模型。为了提高传统指数趋近的控制性能,文中设计了一种具有自适应调节控制参数能力的变速率趋近律方法,并将此方法应用到PMSM速度控制器的设计中。通过与传统PI控制进行比较,仿真和试验结果验证了算法具有较好的动态性能,提高了系统的运动品质。
[1] 杨书生,钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计[J].中国电机工程学报,2009,29(3): 84-89.
[2] GHAFARI K A R, FAIZ J, YAZDANPANAH M J. Integration of non-linearH∞and sliding mode control techniques for motion control of a permanent magnet synchronous motor[J]. IET Electric Power Applications, 2010, 4(4): 267-280.
[3] 钱荣荣,骆敏舟,赵江海,等.永磁同步电动机新型自适应滑模控制[J].控制理论与应用,2013,30(13): 1414-1421.
[4] 常雪剑,刘凌,崔荣鑫.永磁同步电机非奇异快速终端可变边界层滑模控制[J].西安交通大学学报,2015,49(6): 53-59.
[5] 卢涛, 于海生,山炳强,等.永磁同步电机伺服系统的自适应滑模最大转矩/电流控制[J].控制理论与应用,2015,32(2): 251-255.
[6] 张晓光,赵克,孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报,2011,31(24): 77-82.
[7] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3): 431-437.
[8] 汪海波,周波,方斯琛.永磁同步电机调速系统的滑模控制[J].电工技术学报,2009,24(9): 71-77.
Sliding Mode Control for Permanent Magnet Synchronous Motor Based on Variable-Rate Reaching Law Method
LIZhongqin
(Mechanical and Electrical Engineering College, Xinxiang University, Xinxiang 453003, China)
In order to improve the control performance of permanent magnet synchronous motor (PMSM) drive system, a siding mode speed control strategy based on an improved reaching law method was proposed. To shorten the reaching time and weaken system chattering of the conventional exponential reaching law, a novel reaching law based on traditional reaching law was proposed, and the method was applied to PMSM drive system. Compared with traditional PI controller, simulation and experiment results showed that the proposed controller improve the system robustness and dynamic performance.
permanent magnet synchronous motor (PMSM); PI control; variable-rate reaching law; sliding mode control
河南省科技攻关项目(162102210068)
李中琴(1979—),女,硕士研究生,研究方向为自动控制技术与应用。
TM 351
A
1673-6540(2017)05- 0022- 05
2016 -10 -21

