三相电压型脉宽调制整流器定频模型预测控制

王 涛, 吴黎明, 张 晓

(中国矿业大学 信息与电气工程学院，江苏 徐州 221008)

三相电压型脉宽调制整流器定频模型预测控制

王 涛, 吴黎明, 张 晓

(中国矿业大学 信息与电气工程学院，江苏 徐州 221008)

针对三相电压型脉宽调制(PWM)整流器有限控制集模型预测控制采样频率高、开关频率不固定的缺点，提出了一种定频模型预测控制方法。通过求解价值函数得到PWM整流器交流侧下一采样时刻所要输出的电压值，利用空间矢量脉宽调制技术输出计算得到的电压值，实现定频模型预测控制。仿真与试验结果表明：所提出的控制算法开关频率恒定，稳态电流谐波含量低，实现了整流器高功率因数运行。

脉宽调制整流器； 定频； 预测控制； 空间矢量

0 引 言

随着电力电子技术的发展，人们对电能质量的要求越来越高。可四象限运行、交流侧电流谐波含量低、直流侧电压可控、可工作于单位功率因数的三相电压型PWM整流器，已经广泛应用于电网滤波、无功补偿、交流调速、风力发电等领域[1-4]。

近年来，一种新兴的控制策略逐步运用到PWM整流器的控制中，即模型预测控制[5-10](Model Predictive Control,MPC)。MPC基于控制对象数学模型的控制策略，其利用控制对象的数学模型和电路中的已知量，预测下一时刻电路中的可控量。采用循环寻优的方式，选择使得价值函数取得最小值的控制动作作为下一时刻功率管的开关动作，具有控制效果好、鲁棒性强的优点[11]。

三相电压型PWM整流器交流侧可以输出8个电压矢量，有限控制集模型预测控制(Finite-Control-Set Model Predictive Control,FCS-MPC)选择其中一个电压矢量作为下一采样时刻整流器的输出电压，瞬态响应速度快，控制算法简单。但是FCS-MPC算法开关频率不固定、稳态电流谐波含量较大，严重阻碍了FCS-MPC的应用。文献[12]根据各电压矢量作用时电流的变化规律，在不同的扇区选择相应的电压矢量作为输出矢量，通过对目标函数求取偏导数得到各矢量的作用时间，利用空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)算法来实现开关频率的恒定。但是，在相邻扇区进行切换时，该方法求取的矢量作用时间会出现负值，就导致在稳态时电流会发生畸变。文献[13]将整流器输出的最大电压幅值及整个圆周角进行N等分，通过将N个电压幅值和相角分别代入目标函数求取最小值的方法求出目标矢量的幅值和相位，然后使用SVPWM算法输出得到的电压矢量，实现开关频率恒定。但是该方法计算量太大，使用DSP等微控制器难以实现。

为了使预测控制开关频率固定，本文提出了一种定频MPC方法，与文献[12-13]所用方法相比，该方法电流谐波含量少、计算量小，具有实际的应用价值。

1 PWM整流器的数学模型

典型的两电平三相电压型PWM整流器主电路拓扑结构如图1所示。图1中，Uga、Ugb、Ugc为电网三相电压；Uca、Ucb、Ucc为整流桥交流输入侧三相电压；iga、igb、igc为网侧电流；L和R分别为进线电感及等效电阻；C为直流母线电容；RL为负载电阻；Udc为直流侧电压；O为电网中点。

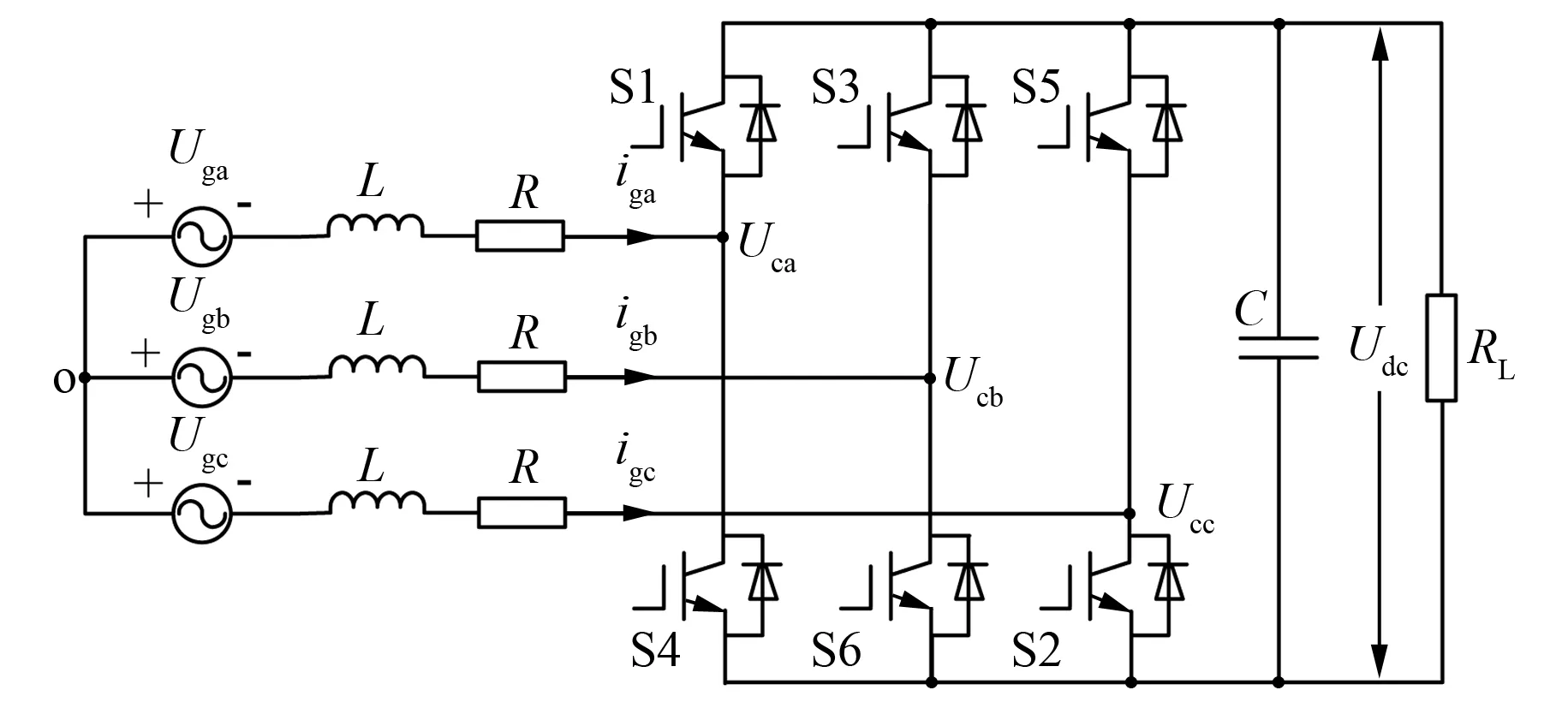
图1 三相电压型PWM整流器主电路拓扑

在三相静止坐标系下，PWM整流器数学模型如式(1)所示。

(1)

(2)

式中:Sa、Sb、Sc——各相桥臂上开关管的开关状态。Sk=1(k=a,b,c)说明k相上管开通，下管关断；Sk=0说明k相上管关断，下管开通。

将式(1)进行Clark变换，可得到两相静止坐标系下PWM整流器的数学模型,如式(3)所示，式(4)是Clark变换矩阵。

(3)

(4)

将式(3)进行Park变换可得到两相旋转坐标系下的数学模型如式(5)所示，式(6)是Park变换矩阵。

(5)

(6)

2 有限控制集MPC

取Ts为控制系统的采样周期，采用前向欧拉算法将式(5)进行离散化表述，可以得到如式(7)所示的离散PWM整流器电流环的预测模型：

(7)

式中:igd(k)、igq(k)——k时刻网侧电流的采样值；

Ugd、Ugq——k时刻网侧电压采样值；

Ucd、Ucq——k时刻整流器输出的控制电压值；

igd(k+1)、igq(k+1)——在k时刻对k+1时刻网侧电流的预测值。

式(7)表明，只要知道了k时刻整流器交流侧电流值、网侧电压值以及整流器输出的控制电压值，即可预测得到k+1时刻网侧电流值。给出性能函数：

(8)

三相电压型PWM整流器交流侧可以输出8个矢量，如图(2)所示。FCS-MPC选择这8个矢量中使目标函数J达到最小值的矢量为作用矢量，使得整流器交流侧电流值在下一采样时刻尽可能的接近给定值。在实际操作中将8个矢量分别代入式(7)中，将产生的预测电流值带入性能函数，选择使J达到最小值的矢量为下一采样周期的输出矢量作用于整流器的交流侧。

图2 电压矢量及扇区定义

3 定频MPC

令k+1时刻网侧电流的预测值和给定值相等：

(9)

设目标函数为

(10)

将式(7)代入式(10)可得

(11)

对式(11)求偏导数：

(12)

可以得到在k时刻输出的控制电压值如式(13)所示。

(13)

式(13)表示，在第k个采样周期内整流器交流侧控制电压为Ucd(k)′、Ucd(k)′时，在k+1时刻网侧电流值将会等于给定电流值。将得到的控制电压值运用SVPWM进行调制输出，便可以实现开关频率的恒定。在运用SVPWM进行调制时，为了保证不过调制，因此得到的Ucd(k)′、Ucq(k)′要满足：

(14)

如果不满足式(14)条件，则令

(15)

本文所提定频MPC算法流程图如图3所示。

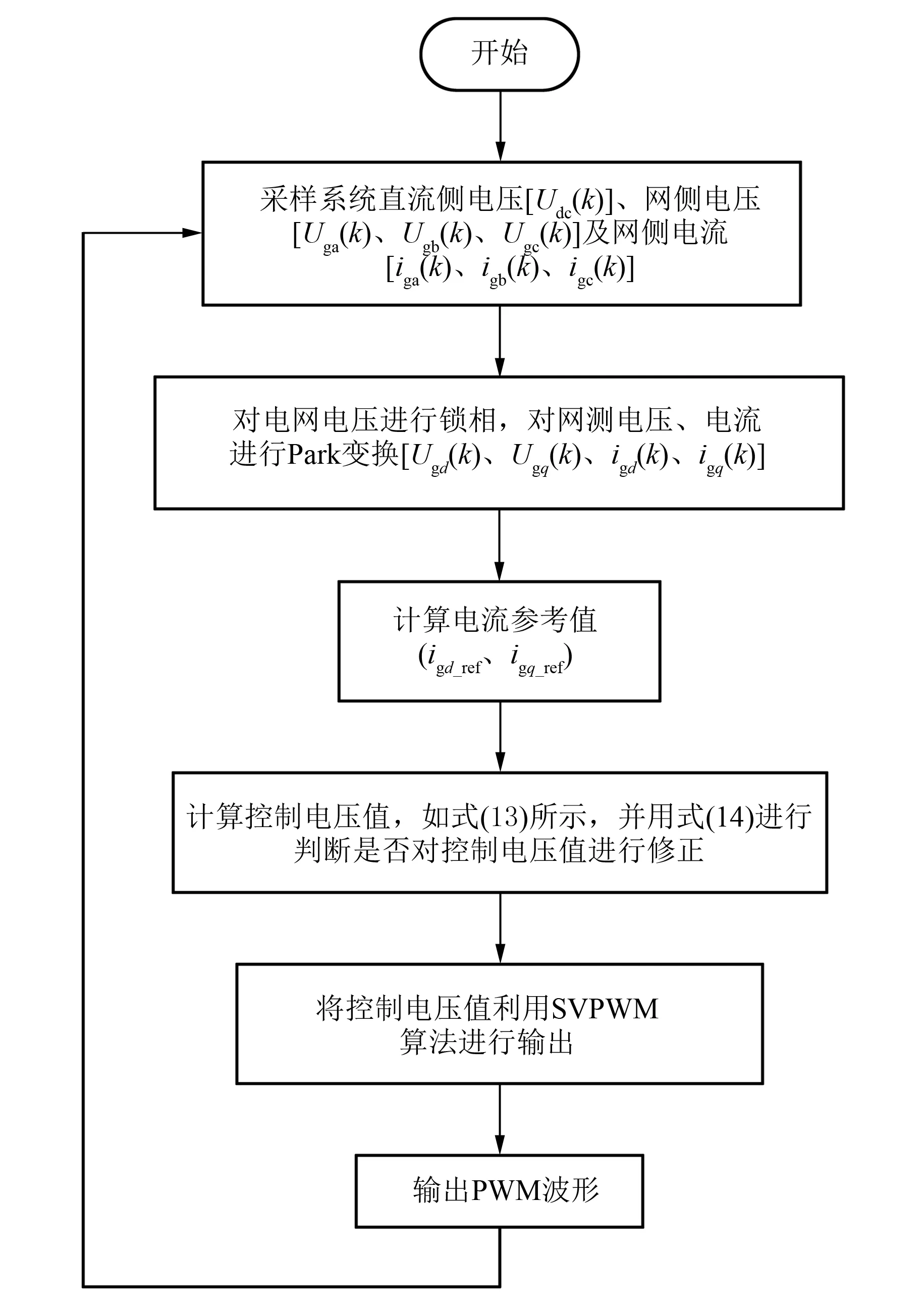
图3 算法流程图

4 仿真与试验

为验证所提定频MPC的正确性和可行性，使用MATLAB和PWM整流器试验平台对所提算法进行了验证。仿真和试验所用参数如表1所示。

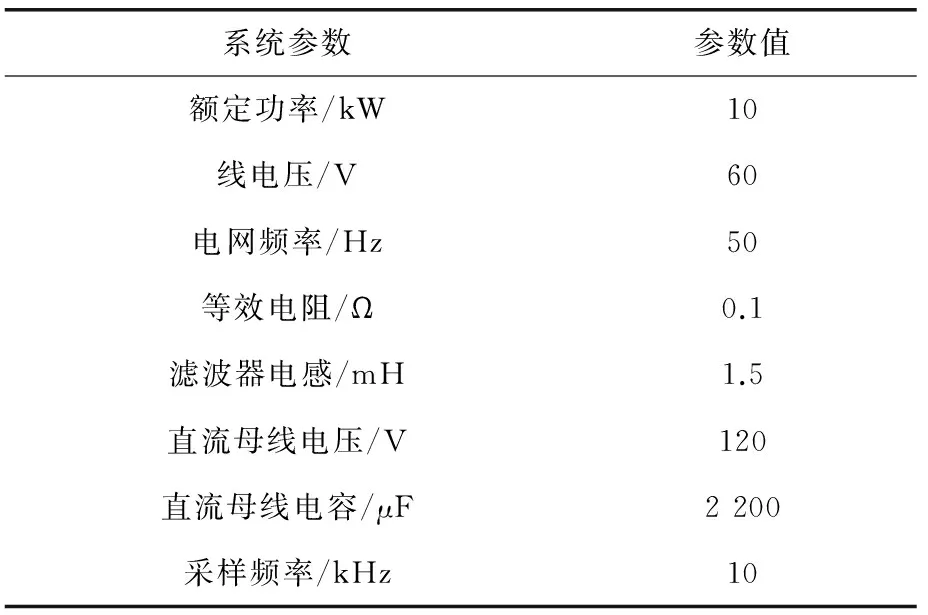
表1 系统参数

为了直观地看到整流器开关管开关频率的变化情况，本文使用Simulink搭建了频率测定模块。其原理类似于电机的M法测速，具体细节如图4所示。

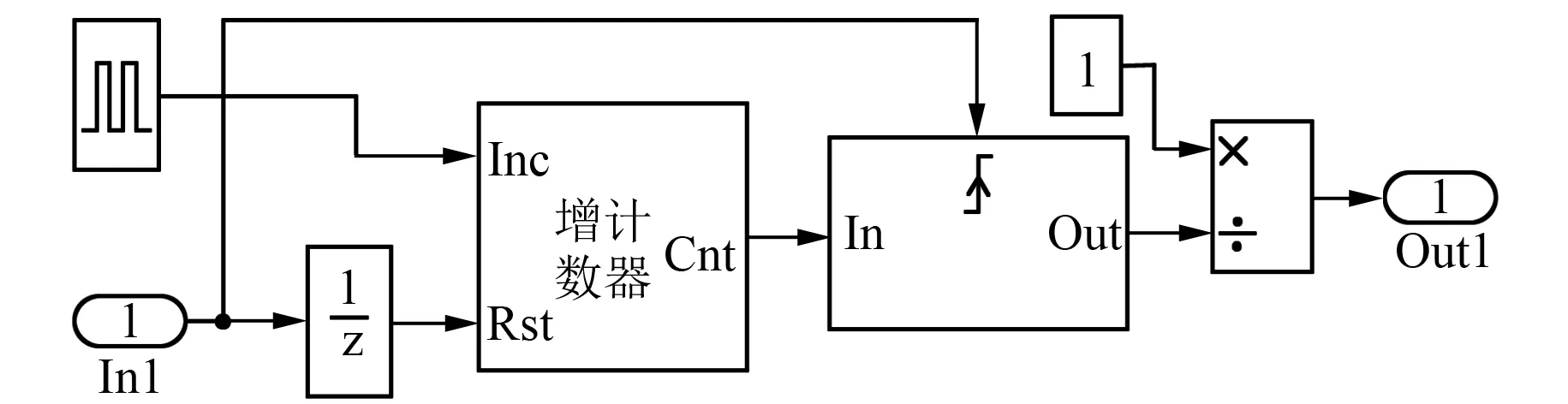
图4 频率测定模块

图4中，In1为待测开关频率信号输入端，Out1为频率输出端。开关管的开关信号通过In1端口输入，经过短暂的延时送入增计数器，计数器在开关信号相邻的两个上升沿之间计算高频信号的个数，将计数得到的高频信号的个数乘上高频信号的周期，再取反便可以得到开关管的开关频率。

由图5～图7可以看到，FCS-MPC算法稳态电流谐波严重，虽然采样频率较高，但是其最高开关频率只有采样频率的一半，平均开关频率小于采样周期的一半，与文献[14]描述的一致；文献[12]所提算法，在相邻扇区切换时，矢量的作用时间会出现负值，就导致稳态电流在扇区切换时发生畸变，而且开关频率也会发生跳变；本文所提算法，稳态电流纹波很小，开关频率恒定。

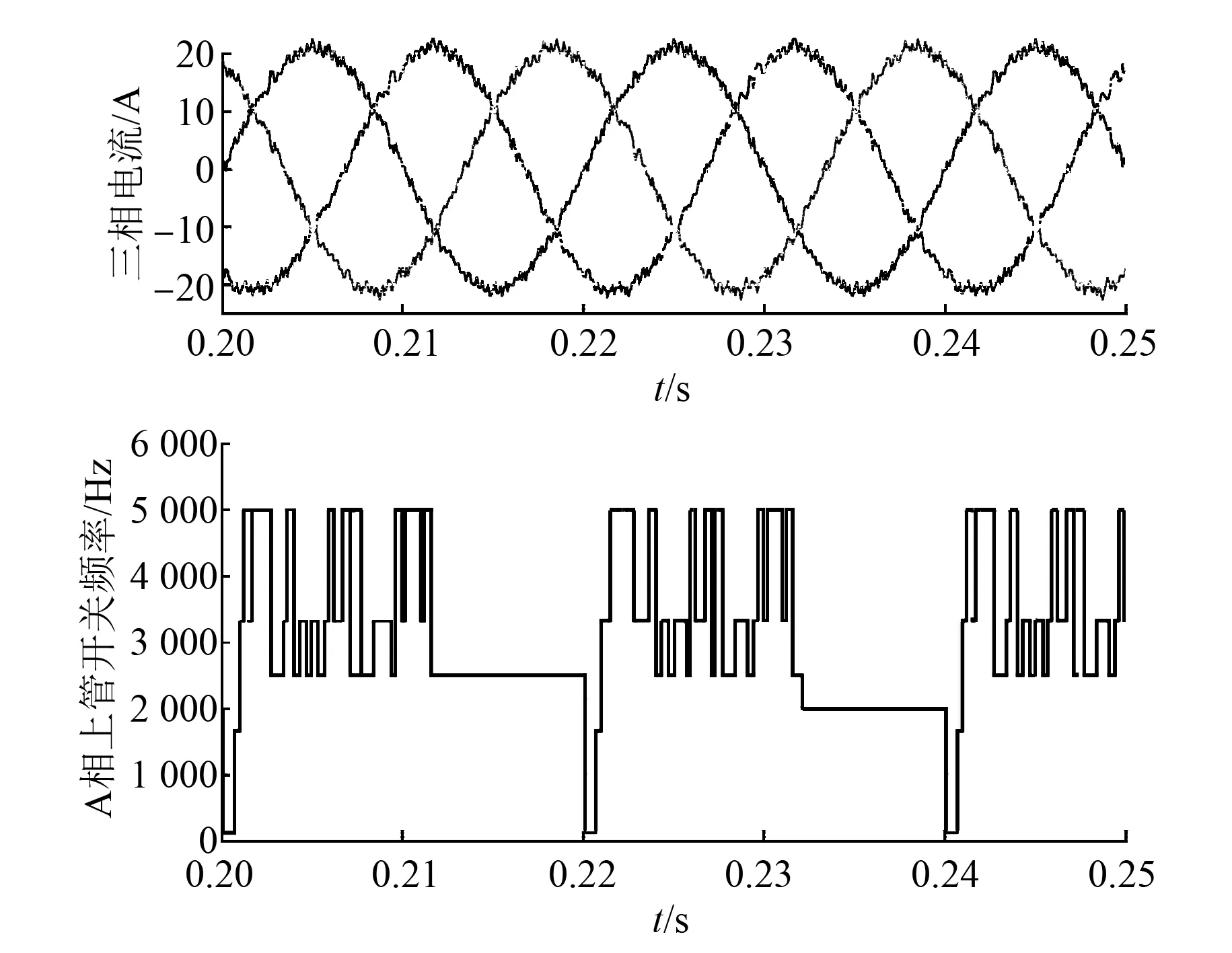
图5 FCS-MPC仿真结果

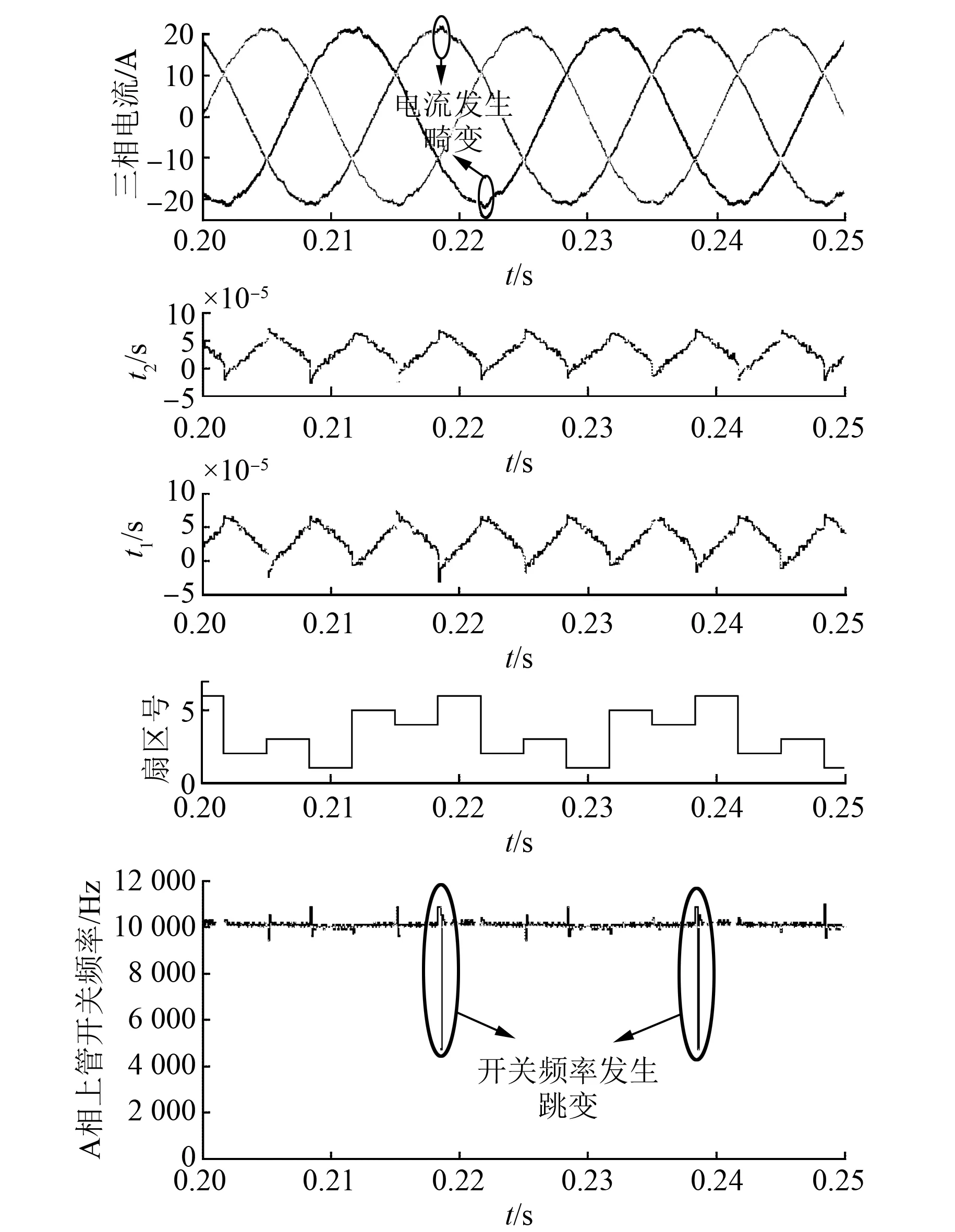
图6 文献[12]所提算法仿真结果

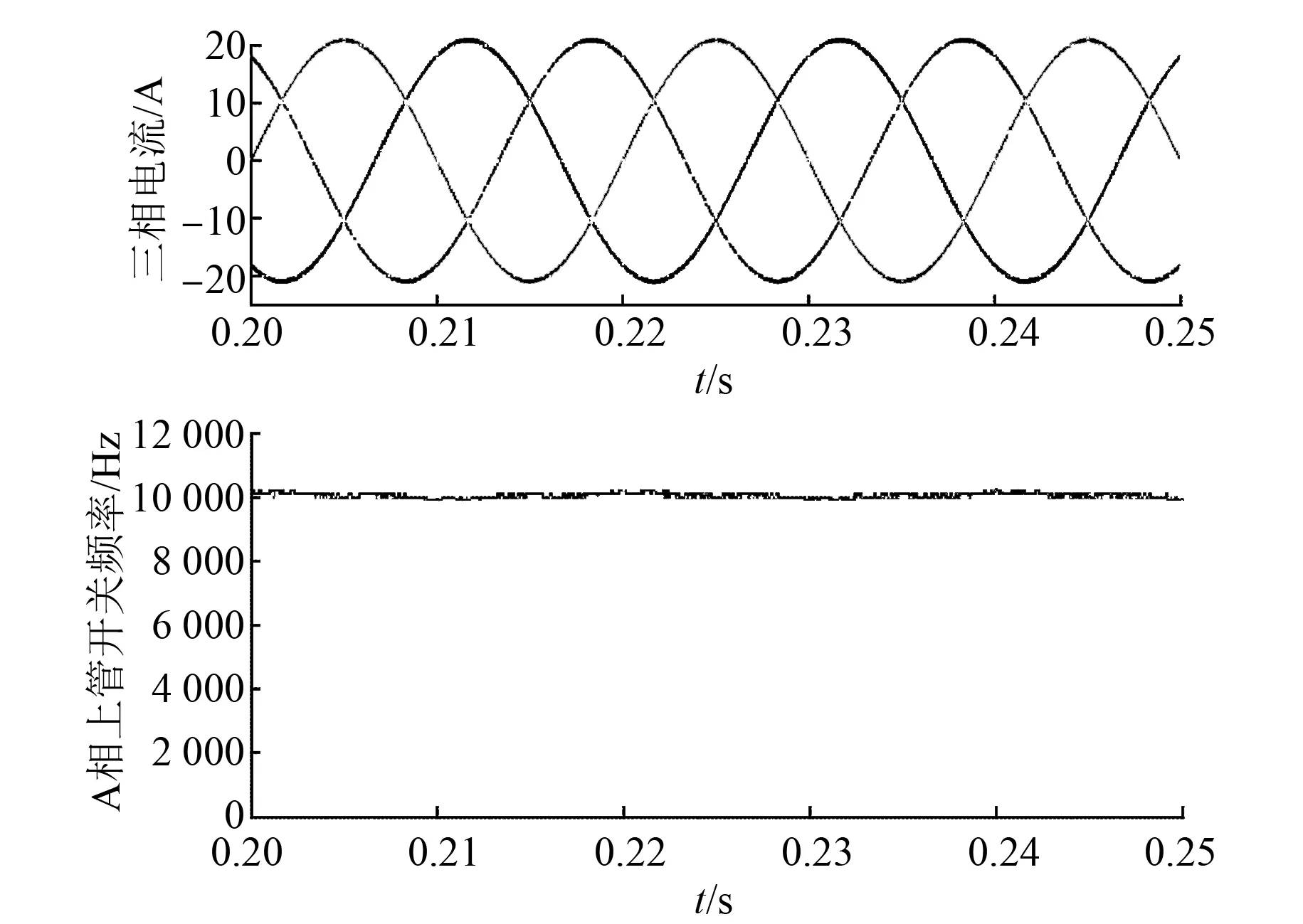
图7 定频MPC仿真结果

图8、图9为FCS-MPC和本文所提算法的试验结果。图8、图9中电流ia为50 A/格，id_ref为d轴给定电流值(用DA输出后进行观测，因此没有量纲)，id_ref从20 A突变到40 A。从图8、图9中可以看出，有限控制集MPC算法动态响应速度快，但是电流谐波比较大，稳态性能较差；定频MPC动态响应速度快，电流谐波含量低，稳态性能好。

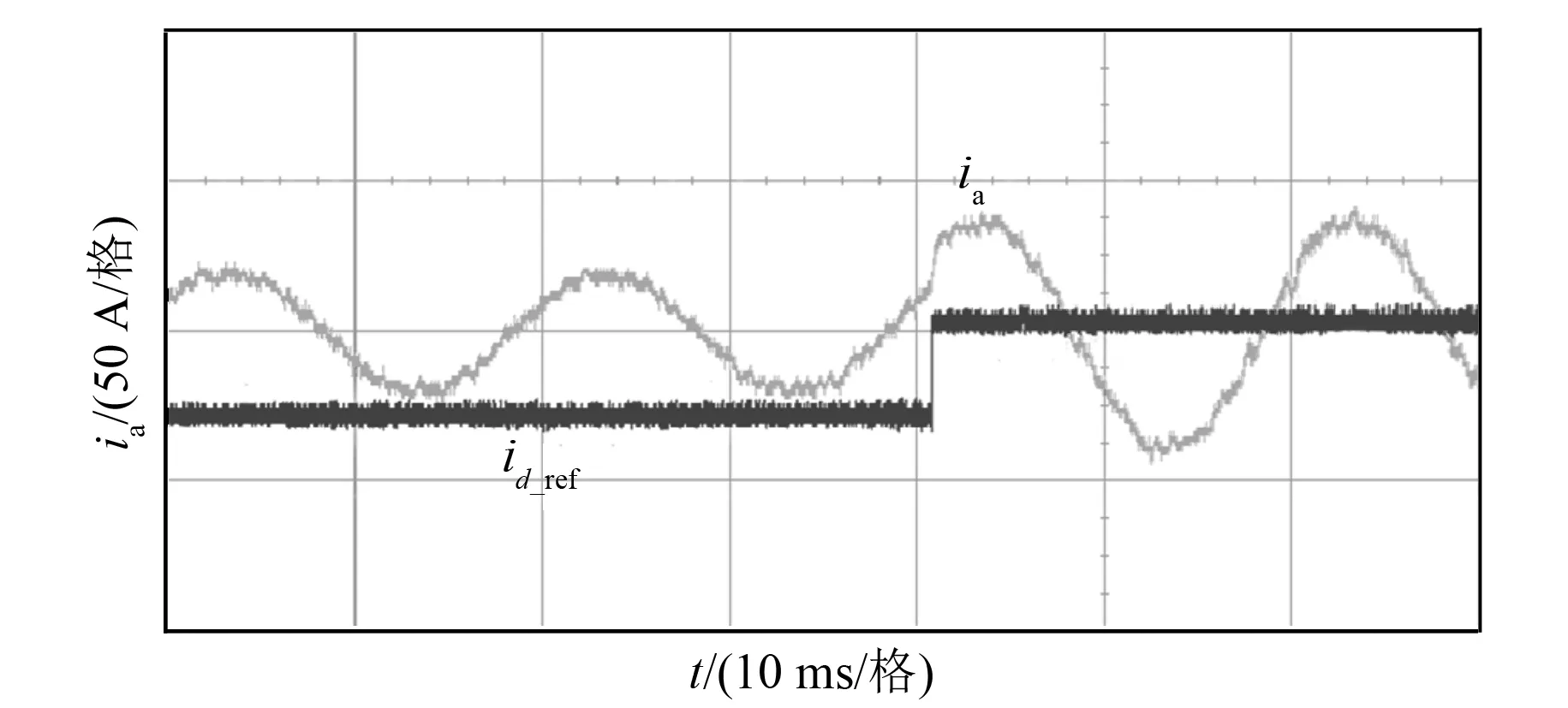
图8 FCS-MPC试验结果

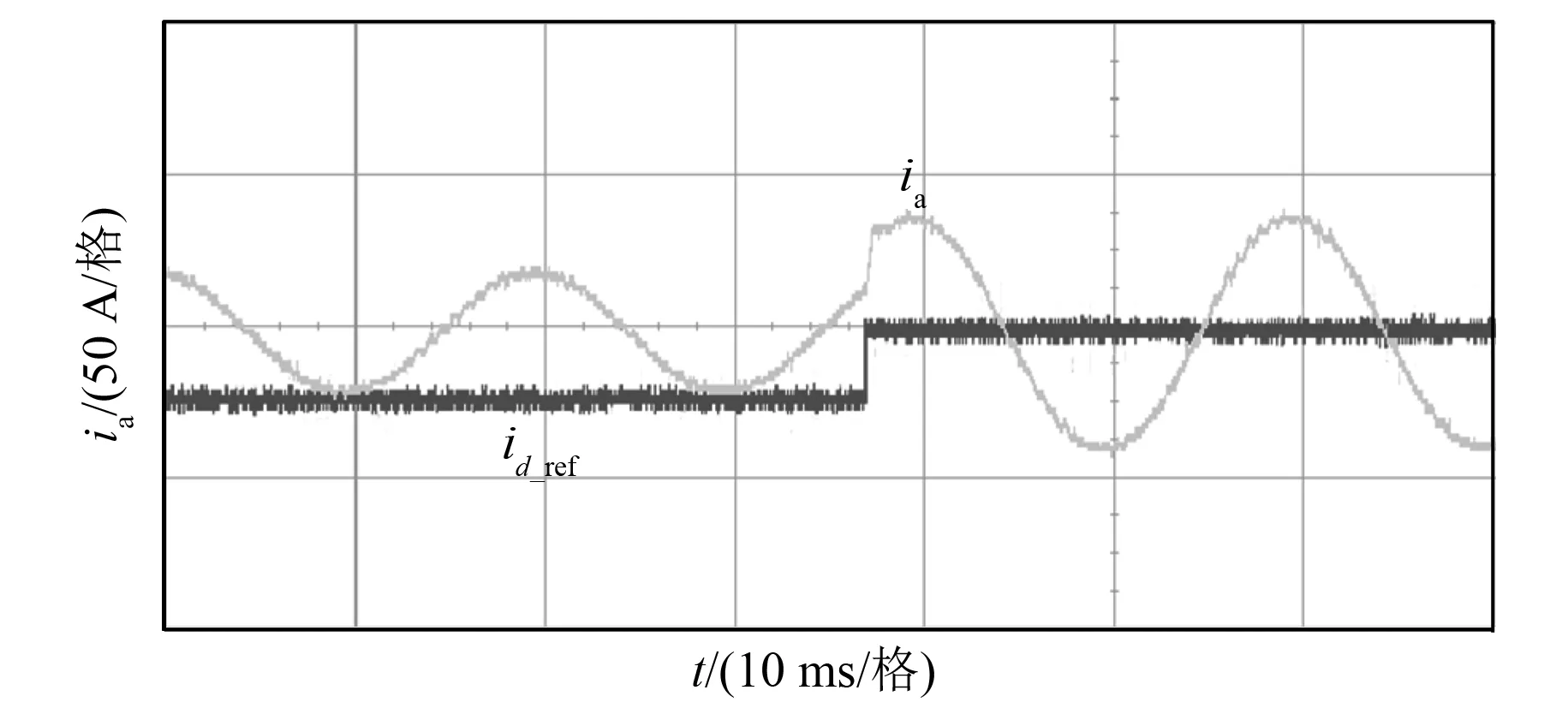
图9 定频MPC算法试验结果

5 结 语

FCS-MPC开关频率不固定，不仅使整流器稳态电流谐波含量增大，而且给进线电抗器的设计也带来困难。本文将预测控制算法和SVPWM算法相结合，实现了开关频率的稳定。通过仿真和试验可以看出，所提的定频MPC算法，开关频率固定，动态响应迅速，稳态电流谐波含量少，但是关于本算法的稳定性和对参数变化的鲁棒性本文并没有涉及，这将是下一步要进行的工作。

[1] 李国华,张影,汪玉凤,等.基于预测控制的有源电力滤波器选择性谐波补偿方法[J].电网技术,2014,38(10): 2938-2942.

[2] 朱彩虹,黄珊珊,高建森,等.SVG自适应无功检测方法及控制系统的研究[J].电工技术学报,2013,28(2): 309-314.

[3] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3): 431-437.

[4] SONG Z F, XIA C L, LIU T. Predictive current control of three-phase grid-connected converters with constant switching frequency for wind energy systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2451-2464.

[5] KWAK S, MUN S K. Model predictive control methods to reduce common-mode voltage for three-phase voltage source inverters[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5019-5035.

[6] 王萌,施艳艳,沈明辉,等.三相电压型PWM整流器模型自校正预测控制[J].电工技术学报,2014,29(8): 151-157.

[7] 宋战锋,夏长亮,谷鑫.静止坐标系下基于最优时间序列的电压型PWM整流器电流预测控制[J].电工技术学报,2013,28(3): 234-240.

[8] 曹晓冬,谭国俊,王从刚,等.三电平PWM整流器多模型预测控制方法[J].电工技术学报,2014,29(8): 142-150.

[9] 王从刚,何凤有,曹晓冬.三相电压型PWM整流器有限开关序列模型预测电流控制[J].电工技术学报,2013,28(12): 182-190.

[10] 杨兴武,姜建国.电压型PWM整流器预测直接功率控制[J].中国电机工程学报,2011,31(3): 34-39.

[11] 马宏伟,李永东,郑泽东,等.电流环模型预测控制在PWM整流器中的应用[J].电工技术学报,2014,29(8): 136-141.

[12] 王萌,施艳艳,沈明辉.三相电压型PWM整流器定频模型预测控制[J].电机与控制学报,2014,18(3): 46-53.

[13] MA Z X, KENNEL R. FPGA implementation of model predictive control with constant switching frequency for PMSM drives[J]. IEEE Transactions on Industrial Informatics, 2014, 10(4): 2055-2063.

[14] 曹晓冬,谭国俊,王从刚,等.三相PWM整流器模型预测虚拟电压矢量控制[J].中国电机工程学报,2014,34(18): 2926-2935.

Constant Switching Frequency Model Predictive Control of Three-Phase Voltage Type Pulse Width Modulation Rectifier

WANGTao,WULiming,ZHANGXiao

(School of Information and Electrical Engineering, China University of Mining and Technology,Xuzhou 221008, China)

To solve the problem of high sampling rate and uncertain switching frequency in finite-control-set, odel predictive control (FCS-MPC) of three-phase voltage type pulse width modulation (PWM) rectifier, a kind of constant switching frequency method was proposed. The voltage of AC side of rectifier which would be effected in the next sampling period was obtained by solving cost function, then the voltage would be produced by using space vector pulse width modulation method to achieve constant switching frequency. Simulation and experimental results showed that the proposed control algorithm had constant switching frequency, low harmonic content and the rectifier operates with high power factor.

pulse width modulation rectifier; constant switching frequency; model predictive control (MPC); space vector

国家自然科学基金项目(51407183)

王 涛(1991—)，男，硕士研究生，研究方向为整流器预测控制。

TM 461

A

1673-6540(2017)05- 0017- 05

2016 -10 -08