p-内平凡kG-模上的Green对应

黄文林

(中国人民大学 信息学院, 北京 100872)

p-内平凡kG-模上的Green对应

黄文林

(中国人民大学 信息学院, 北京 100872)

将内平凡kG-模扩充为p-内平凡kG-模，并证明了若H是群G的强p-嵌入子群，那么Green对应建立了一个从不可分解p-内平凡kH-模的同构类到不可分解p-内平凡kG-模同构类之间的一一对应.

p-可除模；p-内平凡模； Green对应

在有限群表示论中，p-可除kG-模被称为绝对p-可除kG-模，并被用于研究Green环中的幂零元素[1].文献[2]从可裂迹模的角度对p-可除kG-模也进行了细致地研究，得到将张量积分解为不可分解模直和的方法，还得到与有限群表示相关的几乎可裂序列的结论.

E. Dade[3]首次提出内平凡kG-模，内平凡kG-模在p-块代数的稳定范畴上的自等价和Dade群的结构方面扮演着关键角色，而且与源模和源代数有关的一些问题可以约化到内平凡kG-模上来处理[3-5].本文利用p-可除kG-模，将内平凡kG-模扩充为p-内平凡kG-模.一方面，p-内平凡kG-模是内平凡kG-模的广义化[3];另一方面，任何p-内平凡kG-模也是可裂迹模[2].由此，本文研究了一类特殊的可裂迹模——p-内平凡kG-模.

Green对应在有限群表示论中具有根本的重要性，沿着Green的工作思路，本文得到p-内平凡kG-模上诱导和限制的系列结论，特别地，证明了若H是群G的强p-嵌入子群，那么Green对应建立了一个从不可分解p-内平凡kH-模的同构类到不可分解p-内平凡kG-模的同构类之间的一一对应.

本文设定:p是素数，G是阶含有素因子p的有限群，k是特征为p的代数封闭域；本文中所有的模都是有限生成的，所有的群都是有限群；关于本文的记号和术语，请参考文献[6-7].

1 p-内平凡模及其Green对应

定义 1 对于kG-模V和素数p，若V的任意不可分解直因子的维数能被p整除，则称V为p-可除kG-模[1].

读者可证明下面的关于p-可除kG-模的基本结论.

引理 2 设U和V都是p-可除kG-模，W是kG-模，P是G的真p-子群,则:

1)P-投射kG-模是p-可除kG-模，特别地，投射kG-模是p-可除kG-模；

2)V*是p-可除kG-模；

3)U⊕V是p-可除kG-模，反之也成立；

4)U⊗W是p-可除kG-模；

5) Hom(U，V)是p-可除kG-模；

6)U的直因子是p-可除kG-模，特别地，k不是U的直因子，也不是End(U)的直因子.

2) 限制到代数封闭域k，任何不可分解kG-模是绝对不可分解的[1]，由此，本质上，p-可除kG-模是由素数p控制的，并且文献[1]中的绝对p-可除kG-模即是本文中的p-可除kG-模.

3)p-可除kG-模是一个较大的模类，它包含所有的P-投射kG-模(特别地，所有的投射kG-模)，然而，平凡kG-模k不是p-可除kG-模,从而给出下面的定义.

定义 4 设V是kG-模，若内同态(自同态)模End(V)在kG-模同构的意义下可以分解为平凡kG-模k和p-可除kG-模U的直和，也即End(V)≅k⊕U，则称V是p-内平凡kG-模.

p-内平凡kG-模推广了熟知的内平凡kG-模[3].平凡kG-模k是最简单的p-内平凡kG-模，p-内平凡kG-模的维数与p互素，并且，p-可除kG-模一定不是p-内平凡kG-模.

引理 5 设V是p-内平凡kG-模，W是p-可除kG-模，则：

1)V⊕W是p-内平凡kG-模；

2) 在kG-模同构的意义下，V有唯一一个p-内平凡kG-模直因子.

证明 1) 一方面，有下面典范的kG-模同构

End(V⊕W)≅End(V)⊕End(W)⊕
Hom(V，W)⊕Hom(W，V);

另一方面，由引理2得知End(W)、Hom(V，W)、Hom(W，V)都是p-可除kG-模.综上得知End(V⊕W)是平凡kG-模k和p-可除kG-模的直和，也即V⊕W是p-内平凡kG-模.

2) 相反，设U是V的不可分解非p-可除直因子，则End(U)|End(V)，由Krull-Schmidt定理，以及V是p-内平凡kG-模得知End(U)=k⊕M，这里M是p-可除kG-模，再由定义4得知U是p-内平凡kG-模.

进一步，若X是V的另一个不可分解p-内平凡直因子，且U⊕X|V，则k⊕k|End(V)，矛盾.因此，在kG-模同构的意义下，V有唯一一个p-内平凡kG-模直因子.

引理5表明对于任何p-内平凡kG-模V，在kG-模同构的意义下，V是它的唯一的不可分解p-内平凡kG-模直因子和p-可除kG-模的直和.

引理 6 设G≥H，P是G的p-子群，U是kP-模，以及V是kG-模.

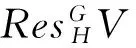
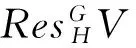
3) 若U不是p-可除kP-模，则IndGHU是p-可除kG-模当且仅当P是G的真p-子群.

证明 1) 由Krull-Schmidt定理可知结论成立.

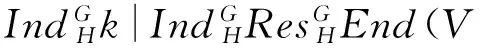
然而，由Frobenius互反律[7]得知

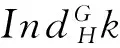
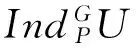
引理 7 设G≥H，V是kG-模,则:

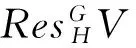
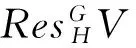
另一方面，

其中M是p-可除kH-模.

2) 设End(V)≅k⊕Y，其中Y是p-可除kG-模,则

性质 8 设U和V都是p-临界kG-模，则U*、U⊗V、Hom(U，V)也都是p-临界kG-模,而且任何p-临界kG-模都是p-内平凡kG-模.

证明 由引理2得知U*和U⊗V都是p-临界kG-模，而且Hom(U，V)也是p-临界kG-模；又因为k是p-内平凡的，结合引理5和7得知任何p-临界kG-模都是p-内平凡kG-模.

性质 9 设V是p-内平凡kG-模,若V是不可分解的，则V的顶是G的西罗p-子群，并且V属于G的满亏p-块；若V是H-投射的，则H包含G的某个西罗p-子群.

证明 反证法.若不可分解模V的顶P是G的真p-子群，则p|dim(V)，矛盾.所以P是G的西罗p-子群，并且V属于G的满亏p-块.若V是H-投射的，则V的不可分解直因子仍是H-投射的，从而H包含G的某个西罗p-子群.

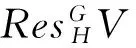
dim(V)=|G∶H|dim(U)，

所以p不能整除dim(V).与此同时，

(1)

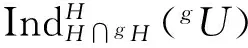
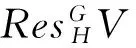
称H是群G的强p-嵌入子群，若p||H|且对于任意x∈G-H有p|H∩xH|；强p-嵌入子群在有限单群分类中有重要的应用；注意到群G的强p-嵌入子群H包含G的任何p-子群在G中的正规化子，以及若群G有平凡西罗交，则G一定有强p-嵌入子群.

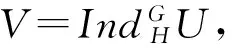
证明 由定理10和强p-嵌入子群定义即知本结论成立.

设H是群G的子群，P是G的p-子群，并且G≥H≥NG(P)，著名的Green对应定理建立了顶为P的不可分解kG-模的同构类和顶为P的不可分解kH-模的同构类之间的一一对应[7].特别地，若P是G的西罗p-子群，V是不可分解p-内平凡kG-模，以及U是不可分解p-内平凡kH-模，下面的结论表明V的Green对应仍是p-内平凡的；然而，一般地，U的Green对应可能是，也可能不是p-内平凡的.

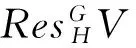
性质 13 设H是G的子群，P是G的西罗p-子群，并且G≥H≥NG(P)；又设U是不可分解p-内平凡kH-模，V是U的Green对应；若对于任何g∈G-H有p||G:H∩gH|，则V是不可分解p-内平凡kG-模.

定理 14 设H是G的子群，P是G的西罗p-子群，并且G≥H≥NG(P)；若H是G的强p-嵌入子群，那么Green对应建立了一个从不可分解p-内平凡kG-模的同构类到不可分解p-内平凡kH-模同构类之间的一一对应.

证明 当H是G的强p-嵌入子群时，推论11和性质12和13共同表明:不可分解p-内平凡kG-模V的Green对应是p-内平凡kH-模，以及不可分解p-内平凡kH-模U的Green对应是p-内平凡kG-模，而且它们有公共的顶P；既然U和V有公共的顶P，以及Green对应建立了具有公共顶的不可分解kG-模的同构类和不可分解kH-模同构类之间的一一对应，综上得知Green对应在不可分解p-内平凡模上封闭，并且也建立了一个从不可分解p-内平凡kG-模的同构类到不可分解p-内平凡kH-模同构类之间的一一对应.证毕.

定理14说明若H是G的强p-嵌入子群，则不可分解p-内平凡模作为顶为P的不可分解模的子类，它的同构类也在从顶为P的不可分解kG-模到顶为P的不可分解kH-模的Green对应下保持封闭.

[1] BENSON D, CARLSON J. Nilpotent elements in the Green ring[J]. J Algebra,1986,104(2):329-350.

[2] AUSLANDER M, CARLSON J. Almost-split sequences and group rings[J]. J Algebra,1986,103(1):122-140.

[3] DADE E. Endo-permutation modules overp-groups II[J]. Ann Math,1978,108(2):317-346.

[4] BOLTJE R, XU B. OnP-permutation equivalences: Between Rickard equivalences and isotypies[J]. Trans Am Math Soc,2008,360(10):5067-5087.

[5] PEREPELITSKY P.p-permutation equivalences between blocks of finite groups[D]. San Diego:University of California,2014.

[6] THEVENAZ J.G-algebras and Modular Representation Theory[M]. New York:Oxford University Press,1995.

[7] WEBB P. A Course in Finite Group Representation Theory[M]. New York:Cambridge University Press,2016.

[8] CARLSON J, MAZZA N, NAKANO D. Endo-trivial modules for the general linear group in a nondefining characteristic[J]. Mathematics,2014,278(3/4):901-925.

[9] CARLSON J, THEVENAZ J. The classification of torsion endo-trivial modules[J]. Ann Math,2005,162(2):823-883.

[10] CRAVEN D. The modular representation theory of finite groups[D]. Birmingham:University of Birmingham,2006.

2010 MSC:20C05; 20C20

(编辑 周 俊)

The Green Correspondence for thep-EndotrivialkG-Modules

HUANG Wenlin

(Schoolofinformation,RenminUniversityofChina,Beijing100872)

In this paper, we extend the ordinary endo-trivialkG-module to thep-endotrivialkG-module, and prove that Green correspondence sets up a bijection between the isomorphism classes of the indecomposablep-endotrivialkG-modules and that of the indecomposablep-endotrivialkH-modules, whenHis stronglyp-embedded inG.

p-divisible module;p-endotrivial module; Green correspondence

2016-11-08

国家自然科学基金(10826057)

黄文林(1977—)，男，博士，主要从事有限群表示论的研究,E-mail:wenlinhuang@163.com

O152.6

A

1001-8395(2017)03-0320-04

10.3969/j.issn.1001-8395.2017.03.008