关于Navier-Stokes-Voight方程精确解的相关探究
刘星辰,马韶光
(南京财经大学 应用数学学院,江苏 南京 210046)
关于Navier-Stokes-Voight方程精确解的相关探究
刘星辰,马韶光
(南京财经大学 应用数学学院,江苏 南京 210046)
研究Navier-Stokes-Voigh(t简称NSV)方程,介绍Navier-Stokes-Voight方程的研究背景,为论文的展开做一些准备工作.利用 Lie群的对称性质求解李方程,最终通过构造标准Lie算子的方法求解一维Navier-Stokes-Voight方程的一维精确解.
Navier-Stokes-Voight方程;Lie-Backlund算子;精确解
0 引言
精确解在偏微分方程理论中占据着重要的位置,通过求解精确解,人们可以给方程以参数得到其数值模拟解,对人们更好地了解流体的发展状态做重要的参考.在众多的求解精确解的方法中,群理论中用对称李群的方法是求解大量偏微分方程的通用工具.
近年来,随机扰动下的无穷维动力系统越来越多地引起人们的注意,其在力学、化学、生物学、地球物理学、大气海洋气候学等中得到广泛应用.本文主要研究随机扰动下的Navier-Stokes-Voigh(t简称NSV)方程.NSV方程描述Kelvin-Voight粘弹性不可压流体的动力学,确定情形下,NSV方程在数学物理各相关问题方面已有不少的结论,具体参见国内外研究现状[1-5].当流体动力学中湍流的影响不能用确定的函数来描述时,引入随机因素是合适而且是必然的.
1 预备知识
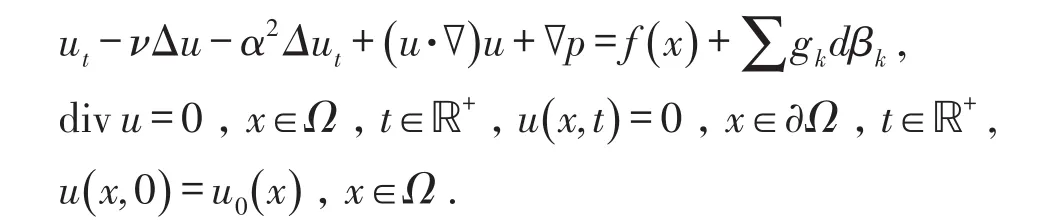
其中Ω是一个带有光滑边界的有界区域,表示给定的外部压力,与时间t相互独立.νΔu表示扩散项,ν>0是粘性系数,gk表示随机压力项.
定义1.1 Sobolev空间[6]
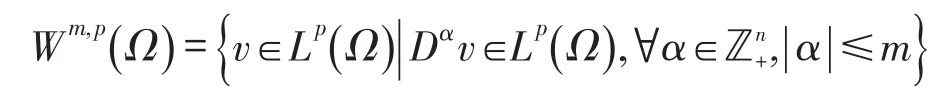
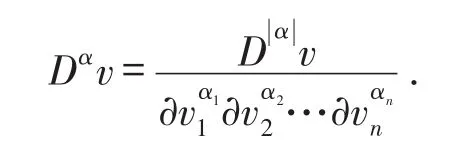
引理1.1 Burkholder-Davis-Gundy(BDG)不等式.
假设T>0,并且(Mt)0≤t≤T是一个连续的局部鞅,M0=0,对于每一个0 cp和Cp和(Mt)0≤t≤T,使得有如下不等式成立: 特殊情况下,取p=2则不等式可化为 引理1.5[7]Young′s不等式 其中q=p/(p-1),1 其中λ1是Stokes算子在齐次Dirichlet边界条件下的第一个特征值. 定义2.1 在此只考虑单个参数的群,设Ta是一个依赖于实参数a,并且作用在(x,y)坐标平面上的变换: 其中和满足边值条件: 定义2.2 如果G包含恒等变换及其逆变换,且它遵循上述群的性质,那么可逆变换的集合G在变量t,x,u的空间下称为单参数变换群. 把函数f,g在a=0的附近进行泰勒展开,把初值条件(2)考虑进去,就可以得到群G的无穷小变换: 式(3)提供群的生成元,即微分算子: 其中X为标准Lie算子. 引理2.1 若F(x,y)是群的不变函数当且仅当如下一阶线性偏微分方程成立 引理2.2 若对称变换有如下形式 对称变换可以写成如下形式 那么这意味着可以找到带有如下对称形式的不变算子 生成元(4)称为方程的一个无穷小对称容许算子. 定义2.4[9]若G是单参数的近似变换群,考虑如下函数 根据引理2.2,找到Navier-Stokes-Voight方程的延拓形式的Lie算子.其中NSV方程为: 可以得到延伸的Lie-Backlund算子 其中α2为正的无穷小量.计算出关于X0的决定方程和生成元,其中 对u,t,x进行变量替换,那么新变量满足方程(4),对进行Taylor级数展开,并且只保留关于a的线性项,那么可以得到下列展开式: 这里Dt和Dx分别表示关于t和x的全微分算子: 根据(4)式可知,原方程经过变换得: 因此,方程需要满足: 即建立的决定方程为 挑选出决定方程(13)中包含的uxx项,从延拓方程中看到只有根据uxx前面的系数可以得到 根据(15)式的信息ξu=0知 把(11)式(12)式带入到算子(7)式中,则可简化为如下形式: 在(16)式中,已经用uxx-uux替换掉ut-αutxx,使得方程更加简洁. 那么将方程(16)化简整理,可以分成如下3个方程: 根据方程ηuu=0可知,ξ关于u至多是线性的,又因为ξxx=2ηux,所以η可以设为如下形式: 又由(18)式可得: 所以得到 根据方程(22)可以得到: 综合上述信息,得到 关于X8有两个自变量,一个是x,另外一个是从特征方程得到的.因此得到积分不变量为因此,在或者中寻找不变解.那么偏微分方程 降至一阶常微分方程 [1]FLANDOLI F,GATAREK D.Martingale and stationary solutions for stochastic Navier-Stokes equations[J].Prob Theory Relat Fields,1995,102:367-391. [2]GAO H,SUN C.Random dynamics of the 3D stochastic Navier-Stokes-Voight equations[J].Nonlinear Analysis Series B:Real World Applications,2012,13:1197-1205. [3]OSKOLKOV A P.On the theory of Voight fluids[J].Zap Naûcn Sem Leningrad Otdel Mat Inst Steklov LOMI,1980,96:233-236. [4]KUBERRY P,LARIOS A.Numerical approximation of the Voigtregularization for incompressible Navie–Stokes and magne⁃tohydrodynamic flows[J].Computers&Mathematics with Applications,2013,354:2647-2662. [5]SUN C,GAO H.Hausdorff dimension of attractor for stochastic Navier-Stokes-Voight equations and primitive equations[J].Dynamics of PDE,2010,7:307-326. [6]CAPINSKI M,CUTLAND N J.Statistical solutions of stochastic Navier-Stokes equations[J].Indiana Univ Math J,1994,43 (3):927-940. [7]LIONS P L.Mathematical topics in fluid mechanics compressible models[M].Oxford:Oxford University Press,1998. [8]CAO C,TITI E S.Global well-posedness of the three-dimensional primitive equations of large scale ocean and atmosphere dynamics[J].Ann Math,2007,166:245-267. [9]LIONS J L,TEMAM R,WANG S.On the equations of the large-scale ocean[J].Nonlinearity,1992,5:1007-1053. [10]EWALD B,PETCU M,TEMAM R.Stochastic solutions of the two dimensional primitiveequations of the ocean and atmo⁃sphere with an additive noise[J].Anal Appl,2007,5:183-198. [11]OSKOLKOV A P.The uniqueness and solvability in the large of boundary value problems for the equations of motion of aqueous solutions of polymers[J].Zap Naucn Sem Leningrad Otdel Mat Inst Steklov(LOMI),1973,38:98-136. [12]GRIGORIEV Y N,IBRAGIMOV.Symmetries of integro-differential equations.With applications in mechanics and plasma physics[M].Berlin:Springer Press,2010. [13]GUILLÉN-GONZÁEZ F,MASMOUDI N,RODRGÍUEZ-BELLIDO M A.Anisotropic estimates and strong solutions of the primitive equations[J].Diff Integral Eqn,2001,14:381-408. Some Research on Navier-Stokes-Voight Equation LIU Xingchen,MA Shaoguang In this paper,the Navier-Stokes-Voight(NSV)equation has been studied.Firstly,we mainly intro⁃duce the research background of Navier-Stokes-Voight equation,at the same time,we do some preparation for the paper.Secondly,by the symmetry of Lie group,we solve the Lie operator.Finally we provide one of the exact solution of one dimensional Navier-Stokes-Voight equation by constructing standard Lie operator method. Navier-Stokes-Voight equation;Lie-Backlund operator;the exact solution O 175.2 A 2095-0691(2017)02-0019-06 2016-11-21 刘星辰(1992— ),男,江苏泗阳人,硕士生,研究方向为偏微分方程理论及应用.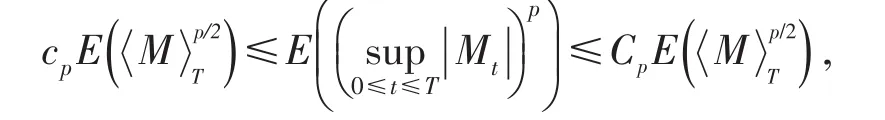
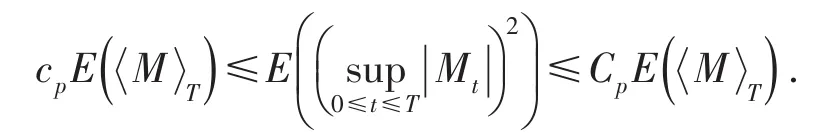
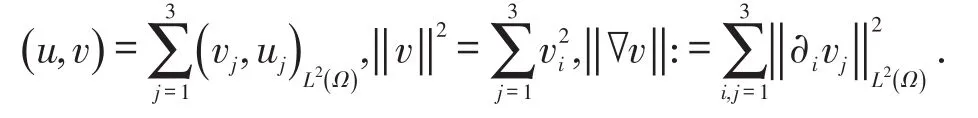
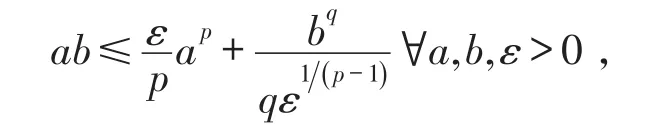
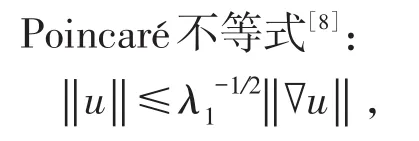
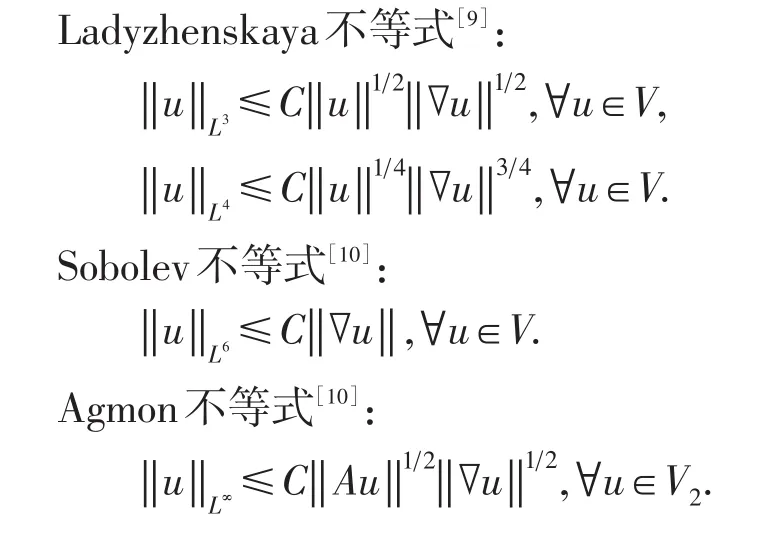
2 一维NSV方程的精确解


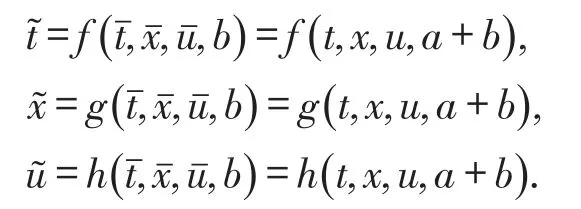
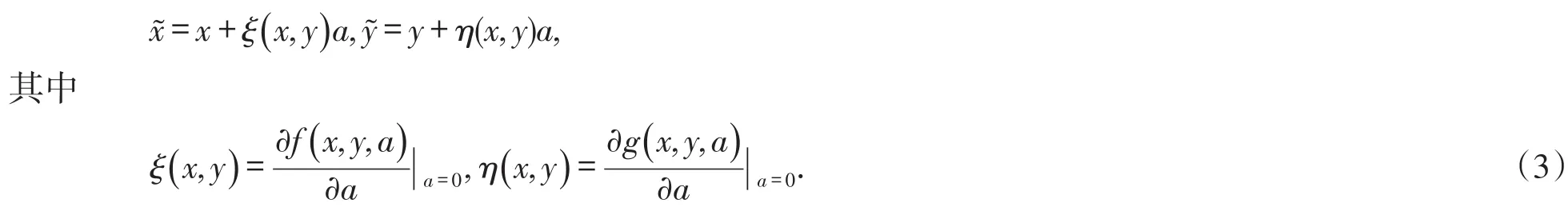
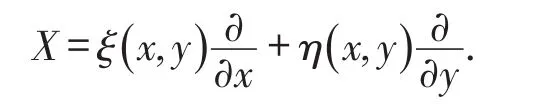
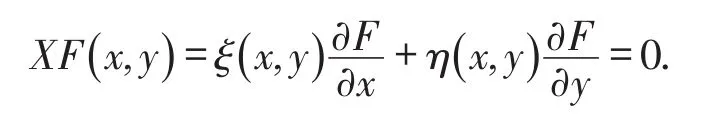
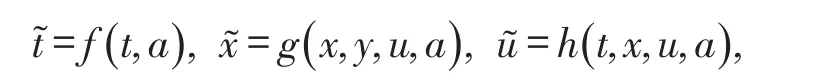


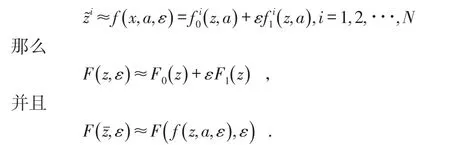


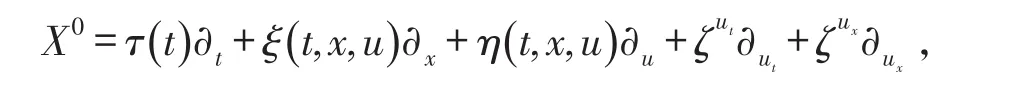
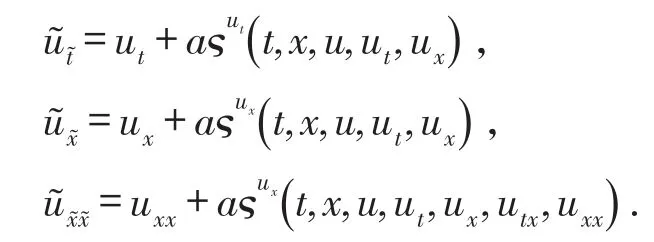
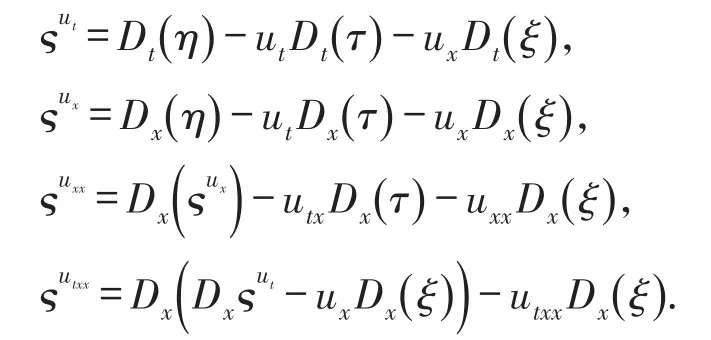
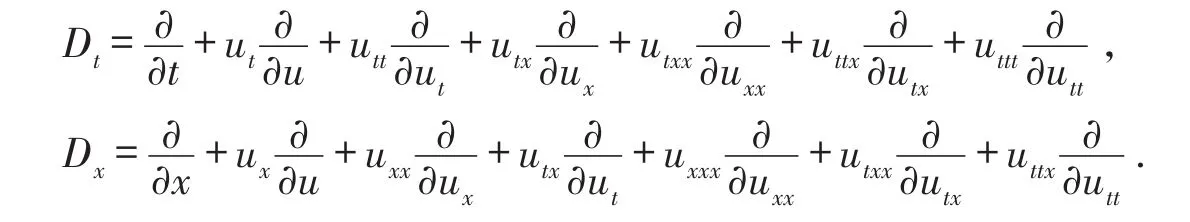
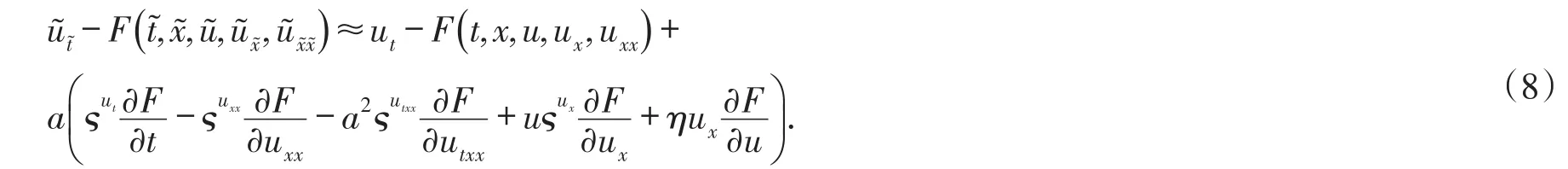
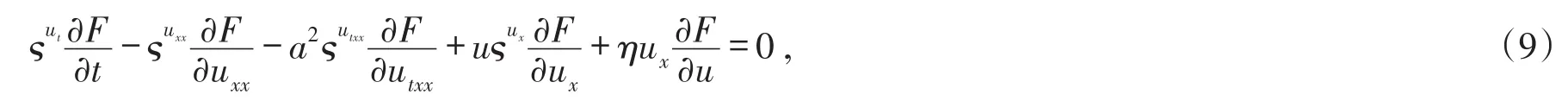

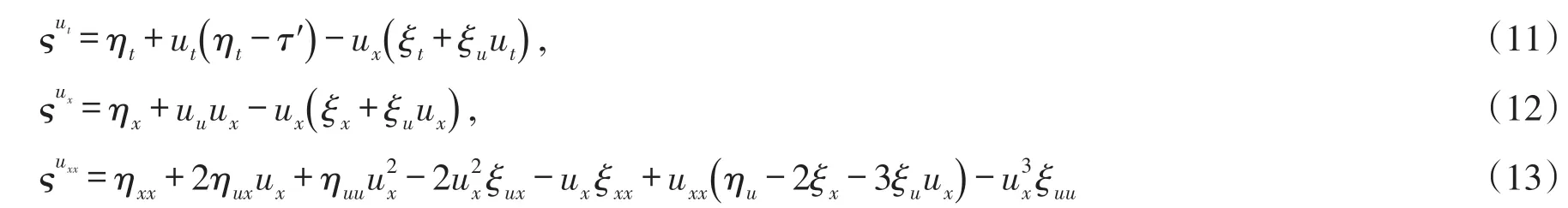

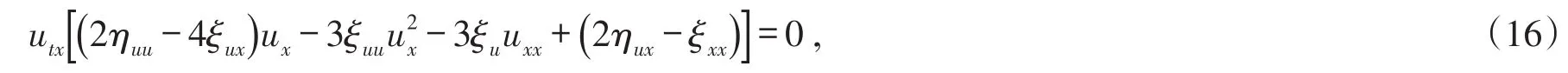

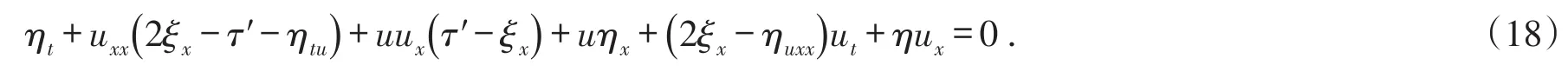

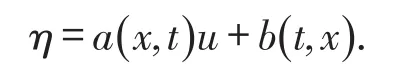
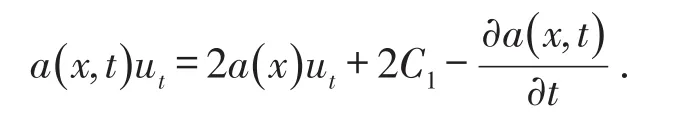


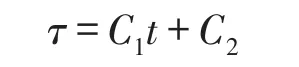
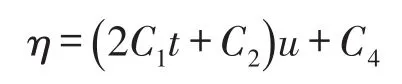
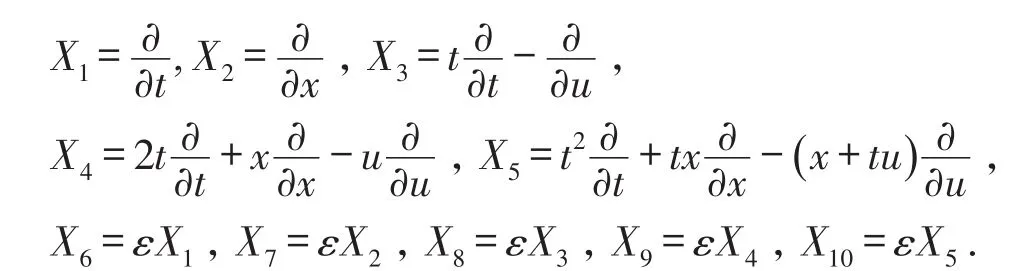
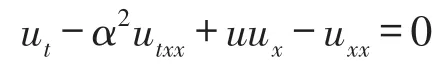
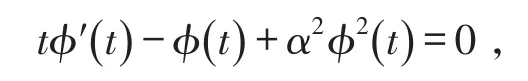
(School of Applied Mathematics,Nanjing University of Finance and Economics,210046,Nanjing,Jiangsu,China)

