基于混合分数布朗运动环境的Black-Scholes模型新解法
孙娇娇,芮绍平,张 杰
(淮北师范大学 数学科学学院,安徽 淮北 235000)
基于混合分数布朗运动环境的Black-Scholes模型新解法
孙娇娇,芮绍平,张 杰
(淮北师范大学 数学科学学院,安徽 淮北 235000)
文章研究不具有平稳增量的随机过程下的欧式期权定价问题.假设标的资产价格变化过程由混合分数布朗运动来刻画,在此环境下研究欧式看涨期权.利用复制策略得到欧式看涨期权价值所满足的偏微分方程.结合欧式看涨期权价值满足的终端条件,运用Mellin变换得到偏微分方程的解析解,即混合分数布朗运动环境下欧式看涨期权定价公式.
混合分数布朗运动;Mellin变换;复制策略;解析解
0 引言
期权定价是金融数学领域中极其重要且值得深入研究的一个问题.起初,人们常用布朗运动来描述金融资产价格的流动性,即得出资产的收益率服从对数正态分布.然而,近些年来,大量的实证研究表明,资产的回报具有长期依赖性、自相似性等特点.为了更好地描述金融资产所满足的这些特点,Cherid⁃ito等[1-2]提出混合分数布朗运动,并把它作为经典Black-Sholes模型的改进,并且混合分数布朗运动刻画的金融环境将不存在套利机会,而且在一定的限制条件下是半鞅.混合分数布朗运动是一族高斯过程,它是布朗运动与分数布朗运动的线性组合.当参数时,混合分数布朗运动是一个特殊的长记忆过程.因此,后来的一些学者对混合分数布朗运动下的期权定价问题展开深入的研究.Sun[3]研究混合分数布朗运动环境下的欧式汇率期权的定价问题,陈飞跃等[4]运用混合分数布朗运动Itô公式,通过热传导方程经典解的形式来求解偏微分方程,获得混合分数布朗运动环境下支付红利的欧式看涨期权的解析式.
近些年来,众多学者运用Mellin变换来求不同类型期权的价值.Panini等[5]首次运用Mellin变换推导出永久美式看跌期权价值所满足的表达式.Yoon[6]利用此方法得到Hull-White随机利率模型下欧式期权的解析解.接着,Yoon等[7]利用双重Mellin变换找到Hull-White随机利率环境下欧式障碍期权的定价公式.在我国利用Mellin变换来求解期权价值的文献还比较少,程凤林等[8-9]运用Mellin变换推出标准布朗运动环境下带交易费用的欧式期权价值满足的数学公式.本文主要运用Mellin变换得到混合分数布朗运动环境下欧式期权的定价公式,这为该模型下的期权定价提供新的研究方法,并且可将此方法用于奇异期权的定价研究.
1 预备知识
1.1 混合分数布朗运动的定义与性质
定义1设(Ω,F,P)是一完备的概率空间,混合分数布朗运动是指以α,β和H为参数的分数布朗运动和布朗运动的线性组合,其公式如下:

其中Bt是布朗运动,是以H∈(0,1)为Hurst指数的分数布朗运动,α和β是两个实常数,且α≠0,β≠0.
根据定义,混合分数布朗运动具有以下性质:
性质3 对任意的s,t∈ℝ+,的协方差函数为
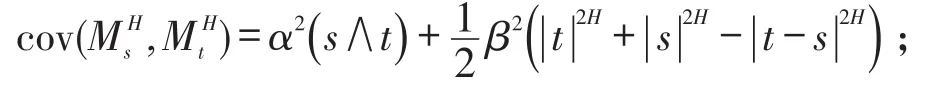
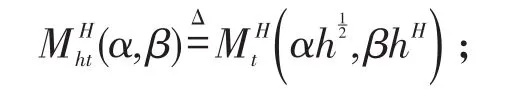
这些性质详细的说明,请参阅文献[10].
1.2 Mellin变换


其中a 引理1(Mellin变换的卷积公式) 假定Mellin变换存在,则对于可积函数x∈ℝ+,利用可给出f和g的卷积公式: 2.1 模型假设 1)买卖证券过程中不考虑交易费用,即市场是无摩擦的; 2)证券交易是连续进行的; 3)不存在无风险套利机会; 4)投资组合每隔δt时间段调整一次,其中δt表示较小的时间步长; 其中短期市场利率r是常数. 6)令St为标的资产在t时刻的价格,假定其满足如下随机微分方程: 其中股票的期望回报率μ,波动率σ1,σ2均为非负常数.布朗运动Bt和分数布朗运动是相互独立的,则股票价格St满足混合分数布朗运动过程,并在以下研究中假定 2.2混合分数布朗运动下的Black-Scholes模型 定理1 设Ct=C(St,t)为欧式看涨期权在t时刻的价格,则在股票价格满足混合分数布朗运动环境下欧式看涨期权所满足的偏微分方程为 且Ct满足以下终端条件 在[t,t+δt]时间段内,投资组合的价值Πt的变化量为 其中δSt,δDt分别表示股票价格和无风险债券价格的变化量. 由于时间步长δt很小,从而由Taylor公式得期权价格在时间区间[t,t+δt]内的变化量如下: 由假设3)知,为了降低套利机会,投资组合的价值必定等于期权的价值,即 由假设4),交易仅发生在t和t+δt处,故由公式(12)和(13)得 从而得到混合分数布朗运动环境下的Black-Scholes方程(8). 在这一部分主要是运用Mellin变换来求出偏微分方程(8)的解析解,由此得到以下定理2. 定理2 假定到期日为T,敲定价格为K,则混合分数布朗运动环境下欧式看涨期权在任意时刻的价格Ct为 其中 Φ(⋅)为标准正态分布累积函数. (16)式常微分方程的解为 根据Mellin逆变换的定义得 将k1,k2代入(22)式并整理即得混合分数布朗运动环境下欧式看涨期权的定价公式(15). 本文假设标的资产价格由混合分数布朗运动驱动,利用复制策略得到欧式看涨期权价值所满足的偏微分方程.结合欧式看涨期权价值满足的终端条件,运用Mellin变换得到混合分数布朗运动环境下欧式看涨期权价值的定价公式.采用混合分数布朗运动来刻画标的资产价格变化过程更符合现实的金融环境,在某种程度上对经典Black-Scholes模型有所改进. [1]CHERIDITO P.Regularizing fractional Brownian motion with a view toward stock pricing modeling[D].Swiss Zurich: Swiss Federal Institute of Technology Zurich,2001. [2]MISHURA Y S,VALKEILA E.The absence of arbitrage in a mixed Brownian–fractional Brownian model[J].Proceed⁃ings of the Steklov Institute of Mathematics,2002,237:224-233. [3]SUN Lin.Pricing currency options in the mixed fractional Brownian mode[lJ].Physica A,2013,392(16):3441-3458. [4]陈飞跃,杨蓉,龚海文.混合分数布朗运动环境下欧式期权定价[J].经济数学,2014,31(3):9-13. [5]PANINI R,SRIVASTAV R P.Option pricing with Mellin transforms[J].Math Comput Model,2004,40:43-56. [6]YOON J H.Mellin transform method for European option pricing with Hull-White stochastic interest rate[J].J Appl Math,2014:1-7. [7]YOON J H,KIM J H.The pricing of vulnerable options with double Mellin transforms[J].J Math Anal Appl,2015,422 (2):838-857. [8]程凤林,申红莲.Mellin变换在欧式期权定价中的应用[J].衡水学院学报,2009,11(4):18-20. [9]程凤林,李乐.Mellin变换在推广的欧式期权定价中的应用[J].衡水学院学报,2011,13(4):98-101. [10]ZILI M.On the mixed fractional Brownian motion[J].International Journal of Stochastic Analysisl,2006,2006:1-9. New Solution of Black-Scholes Model Under Mixed Fractional Brownian Motion SUN Jiaojiao,RUI Shaoping,ZHANG Jie European option pricing is studied under stochastic process with no stationary increment.Assuming that the underlying asset price change process is described by mixed fractional Brownian motion,we start the study of European call option.Replication strategies are used to get the partial differential equation of the Eu⁃ropean call option value.Combined with European call option value of terminal conditions,we use Mellin transform to derive the analytic solution of the partial differential equation.The pricing formula of European call option is obtained under mixed fractional Brownian motion. mixed fractional brownian motion;mellin transform;replication strategies;analytic solution O 211.6;F 830.9 A 2095-0691(2017)02-0001-05 2017-01-20 安徽省自然科学基金项目(1508085SMA204) 孙娇娇(1987— ),女,安徽怀宁人,助教,硕士,研究方向:金融数学.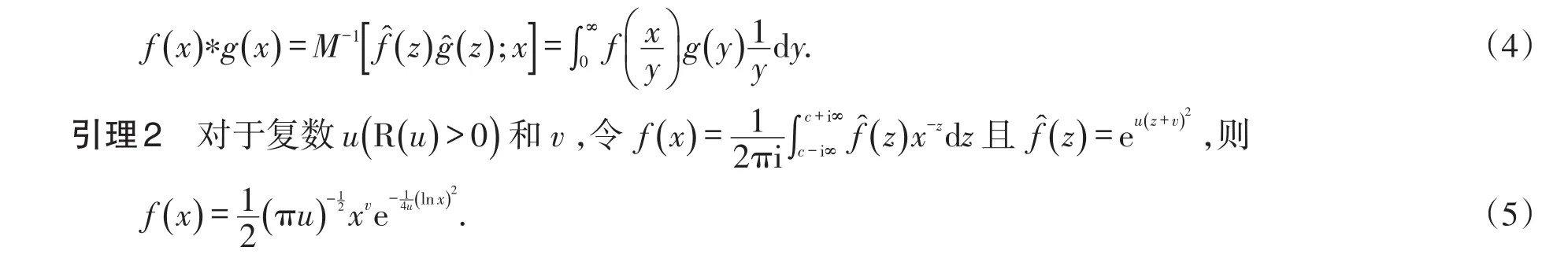
2 金融市场期权价格模型


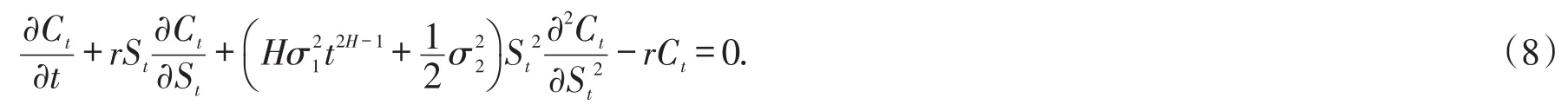





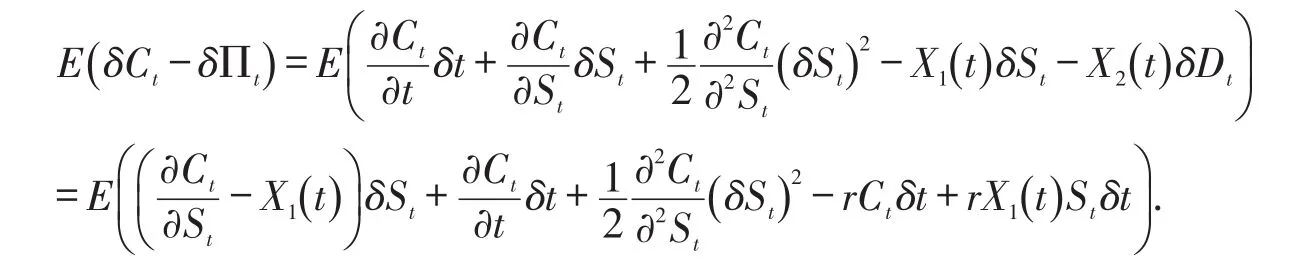
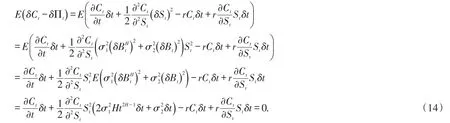
3 模型的求解

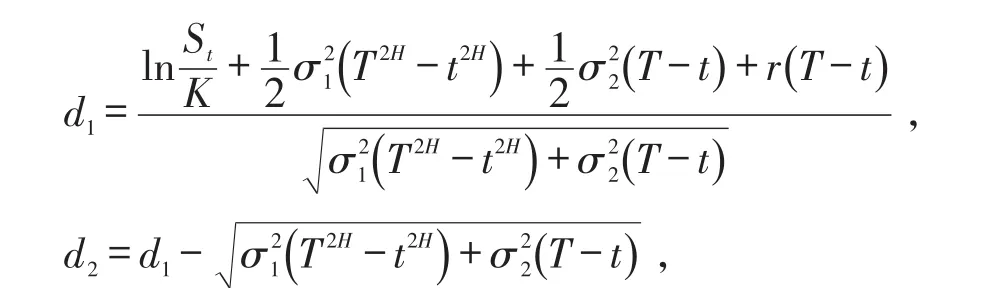

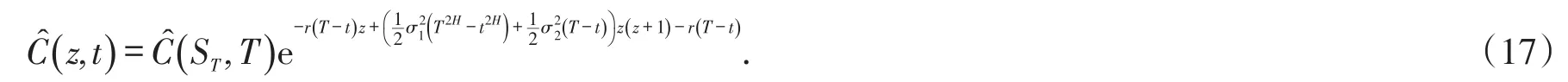

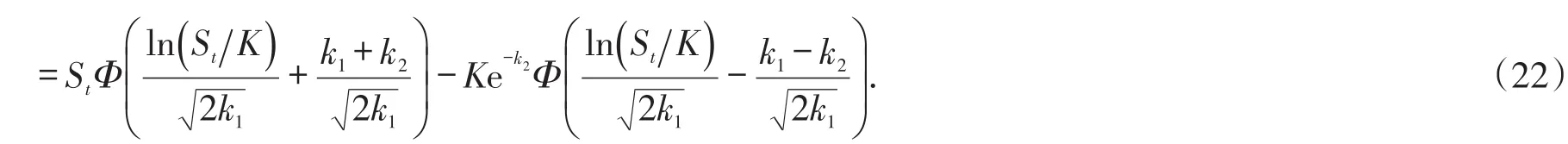
4 结论
(School of Mathematical Sciences,Huaibei Normal University,235000,Huaibei,Anhui,China)

