一道课本习题的改编与赏析

广东省惠州市惠阳区华南师范大学附属惠阳学校 林永珍

一道课本习题的改编与赏析

广东省惠州市惠阳区华南师范大学附属惠阳学校 林永珍

纵观近几年全国各地中考试题，其中很多题目都是课本例题习题改编而成，这类题不仅较好地体现了命题的原则，依据大纲，遵循教材，尊重学生，关注课堂，而且紧扣大纲和教材，体现了基础性和学好课本的重要性，有着非常重要的导向作用，不仅能引导师生重视基础，重视教材，研究教材，用好用活教材，而且能激发学生学习数学的兴趣，挖掘例题的功能，促进学生对知识本质的理解。教材是教学必不可少的重要资料，而教材例习题是数学教材的重要组成部分，同时又是检验学生掌握知识程度与能力高低的主要手段，一方面，教材例习题可以起到复习﹑巩固知识，加深学生对知识理解和记忆的作用，另一方面，教材例习题能够启发思维，是培养学生分析问题﹑解决问题能力的重要载体。

下面，我就对新人教版九年级上册第十三章旋转复习巩固习题第5题进行改编赏析。

原题：如图1，△ABC和△ECD都是等边三角形，△ECB可以看作是△DAC经过平移﹑轴对称或旋转得到的。说明得到△EBC的过程。

解：∵△ECD是等边三角形，∴CD=CE，∠DCE=60°，同理CA=CB，∠ACB=60°，

∴以点C为旋转中心，将△DAC逆时针旋转60°就可得到△EBC。

本题以等边三角形为载体，对于旋转问题，首先应明确旋转的性质，哪个是旋转中心，哪些线段是相等的，哪些角是相等的，要用旋转的眼光去观察和研究图形，把握图形旋转的性质。

改编（1）：如图2，连接P﹑Q，求证：△PCQ为等边三角形。

证 明 ∵ △BCE≌ △ACD， ∴ ∠CAD=∠CBE，∵∠BCA=∠DCE=60°，∴∠ACE=180°-60°-60°=60°。在△AQC和△BPC中，∠CAQ=∠CBP，∠ACQ=∠BCP ，AC=BC，∴△ACQ≌△BCP（AAS），∴CP=CQ，∴△CPQ是等边三角形。

改编二：如图3，已知△ABC和△ECD都是等边三角形。

（1）已知B﹑C﹑D三点在一条直线上，求证BE=AD；

（2）保持△ABC不动，将△ECD绕点C顺时针旋转，使∠ACE=90°（如图4），则BC与DE有怎样的位置关系？说明理由。

题目分析：（1）利用等边三角形的性质和已知条件证明△ACD≌△BCE即可；（2）BC垂直平分DE，延长BC交DE于M，证明∠ECM=∠DCM，利用三线合一证明即可。

证明：（1）∵△ABC和△ECD都是等边三角形，∴AC=BC，EC=DC，∠ACB=∠ECD=60°。

∴∠ACB+∠ACE=∠ECD+∠ACE，即∠ACD=∠BCE。∴△ACD≌△BCE。 ∴AD=BE。

（2）BC垂直平分DE，理由如下：

如图5，延长BC交DE于M，

∵ ∠ ACB=60 °， ∠ ACE=90 °，∴∠ECM=180°-∠ACB -∠ACE=30°。∵∠DCM=∠ECD-∠ECM= 30°，∴∠ECM=∠DCM。∵△ECD是等边三角形，∴CM垂直平分DE，即BC垂直平分DE。

试题赏析：本题以三角形为背景，以线段和角的关系为目标，整合三角形的性质﹑全等三角形的判断等知识，充分体现了中考数学考试说明中的以问题为载体，以知识为基础，以思维为主线，以能力为目标，全面考查学生的学习潜能，力求体现出重视基础，关注思想，加强应用，发展能力的试题特征，与学业考试的目标指向：有利于减负，有利于教育均衡相一致的指导思想，教与学立足于基础，注重创新思维的训练，注重学生解决问题能力的培养，力争做到发挥好一个问题背景的作用。

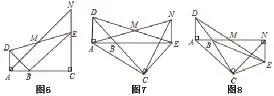
改编三：如图6，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N。

（1）当A，B，C三点在同一直线上时（如图6），求证：M为AN的中点；

（2）将图6中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图7），求证：△ACN为等腰直角三角形；

（3）将图6中的△BCE绕点B旋转到图8位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由。

（1）证明：如图6，∵EN∥AD，∴∠MAD=∠MNE，∠ADM=∠NEM。∵点M为DE的中点，∴DM=EM。

∴△ADM≌△NEM，∴AM=MN，∴M为AN的中点。

（2）证明：如图7，∵△BAD和△BCE均为等腰直角三角形，∴AB=AD，CB=CE，∠CBE=∠CEB=45°。

∵AD∥NE，∴∠DAE+∠NEA=180°，∵∠DAE=90°，∴∠NEA=90°，∴∠NEC=135°。∵A，B，E三点在同一直线上，∴∠ABC=180°-∠CBE=135°。∴∠ABC=∠NEC。∵ △ADM≌ △NEM（ 已 证）， ∴AD=NE。 ∵AD=AB，∴AB=NE。

∴ △ABC≌ △NEC。 ∴AC=NC， ∠ACB=∠NCE。∴∠ACN=∠BCE=90°。∴△ACN为等腰直角三角形。

（3）解：△ACN仍为等腰直角三角形。

证明：如图8，此时A﹑B﹑N三点在同一条直线上。

∵AD∥EN，∠DAB=90°，∴∠ENA=∠DAN=90°。∵∠BCE=90°，∴∠CBN+∠CEN=360°-90°-90°=180°。

∵A﹑B﹑N三点在同一条直线上，∴∠ABC+∠CBN=180°。∴∠ABC=∠NEC。∵△ADM≌△NEM（已证），∴AD=NE。∵AD=AB，∴AB=NE。

试题赏析：本题考查了全等三角形的判定与性质﹑平行线的性质﹑等腰直角三角形的判定与性质﹑多边形的内角与外角等知识，渗透了变中有不变的辩证思想，是一道好题。将课本原题中的等边三角形改为等腰直角三角形，通过类比联想引申拓展，可以达到解一题会一类的目的。

一个多次出现的问题背景，利用曾经证明的结果，稍加改编，就能将动态思想﹑方程思想等在此进行综合应用，通过双基整合﹑数学建模﹑实践操作﹑探究开放综合应用等途径，让学生经历做数学和用数学的过程，发展他们的数学符号感﹑空间感﹑应用意识和数学能力，合理评价学生掌握数学知识和形成数学能力的状况，评价学生的情感态度和价值观。将特殊三角形置于其中，不断更新，改编出一组综合性强，条件简洁直观的问题，关注学生的推理能力﹑探究能力，演绎了旋转的精彩变换。

book=69,ebook=71