学习迁移理论在高中数学教学中的实践应用

江苏省梁丰高级中学 施冬芳

学习迁移理论在高中数学教学中的实践应用

江苏省梁丰高级中学 施冬芳

学习迁移理论是指通过对一个问题的学习，将其思考方式和解决办法迁移到另一个问题的学习中，增加自己的学习效率。学习迁移也可以处在两种科目学习之中，比如通过语文句式的学习可以迁移到英语句式的掌握与应用。所以，学习迁移理论对于学生们来说是比较重要的，可以让学生们了解到知识之间的联系，通过学习迁移理论达到事半功倍的效果。本文将以学习迁移理论在高中数学教学中的实践应用为主题进行详细的分析。

一、提高掌握质量，增强迁移能力

学生们的迁移能力在高中数学教学中表现出来的是多方面思维的解决方法，但是，数学迁移能力首先需要学生们掌握牢固的知识结构。在高中数学教学中，教师要重视双基，强化对数学的基本概念和公式的应用条件的讲解，掌握重点和难点，强化学生们对数学问题的分析﹑思维和总结能力。这样，学生在解题时会迅速联想到相关数学概念和方法。例如：在等差数列{an}中，已知a8≤15，a9≤13，求a12的取值范围。如果有扎实的双基知识，学生很快会联想到线性规划问题，从而促进对问题的解决。同时，加强知识间的联系有利于增强知识的记忆，提高数学迁移能力。在教学中，教师们运用自己完善的知识结构帮助学生们进行知识的整理，构成自己独特的知识结构，让已学的知识系统化，掌握各个数学知识之间的数学联系。学生们应把平时所学的数学零碎知识根据数学问题的解决方法和规律进行联系﹑总结。例如三角函数中的九组诱导公式，学生觉得太难记了，但若能联系三角比的定义和各象限的符号，就很容易得到相应的角之间的关系。比如 与 的关系，根据 和 的终边互为反向延长线，得到终边上点 中 互为相反数，又所以

学生们在构建数学知识框架的时候可以通过以下几个方面进行考虑：第一，各章节知识可以通过一个知识点或者解题方法联系起来，章节与数学整体知识进行结合，形成有层次的数学知识结构框架。第二，教师应向学生们讲解数学知识的规律，总结解题的思路和方法，以此提高学生们对数学知识的分析和解决问题的能力。并根据数学知识在生活中的应用问题，进一步加强学生们的思维能力﹑想象能力和基础运算能力。第三，教师们可以根据教学情况进行章节复习，深化数学知识之间的内在联系，整体提高学生们对数学知识的掌握和应用能力。提高知识掌握质量，主要是使学生构成完整的数学知识结构体系，拥有夯实的数学基础，为培养学生多方法解决问题打下坚实的基础。

另外，教师们可以通过对数学习题的训练来进一步提高和完善学生们的知识掌握能力，不断提高数学迁移能力。数学作为理科中的标志性学科，它不同于其他文科性的学科，其具有较强的逻辑性，是拓宽学生们思维﹑培养学生们多方法解决问题的重要途径。数学的学习没有太多的捷径可走，量变成为质变，强化做题的数量和质量是必不可少的。但是，做题也是有学问的。在做数学题时，一定要避免做一道就直接对答案，因为这样会打断你的做题思路。遇到难题时可先不做，保证自己平稳的心态和做题速度。对付难题时自己一定不要急躁，要有一定的耐心。做一道题要有一道题的收获，掌握每道题所包含的知识点，根据多道相似的问题寻找一定的解决思路和方法。另外，对每道题还要发散思维，自己试试能不能改改题目，变成考查其他知识点的题目，根据多种思路方法寻找新的解决方法，进而形成一题多解的目的。面对错题是自我反思的过程。每个数学思维往往都不是独立的，都有其对立面，在解题受阻时可以换个思路解决问题。领悟数学思维，强化拓展思维，进一步提高学生们的数学素养，多方法解决问题的能力。教师们通过构建学生们的数学知识网络结构以及不断强化数学习题训练，促使学生逐渐熟练地掌握和运用数学基础知识，培养学生们的迁移能力。

二、引导数学方法，增强迁移能力

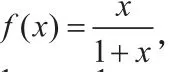
除此之外，教师们可以构建问题意境，发散学生们的思维，激励学生们不同的想法，根据他们不同的思路给出准确的建议。教师鼓励学生们展示自己的想法和思路，在其中找到多种方法解决问题的捷径。虽然在数学课本中给出的数学例题解决方法大多都是唯一的，但是实际情况中，解决问题的方式往往有很多种，根据这些例题对学生多方法解决问题能力进行培养。比如，已知的最大值。本题常规的解法是把看作一个开口向上的二次函数，然后利用数形结合的思想得到当时，取最大值。教师在讲解时还可鼓励学生们用不同的方法解题，如利用基本不等式，即，当且仅当，即时取等号。数学这一学科其本身存在整体性和复杂性,学生们在学习过程中应该有其独特的思维方法，教师应该让学生学会“一题多解”的方式方法, 激发学生们对数学学习的积极性，提高学习效率，增强数学迁移能力。

三、强化数学教学，增强迁移能力

教师们可以在教学中对相关代表性的题目进行详细的讲解，让学生们掌握问题分析的方法，增加学生们的数学迁移能力。对于高中数学，函数知识可以说是贯穿整个数学教学过程，任何一个数学知识都可以与函数相结合形成一道数学题目。所以，教师们要着重对函数知识的讲解，让学生们详细地掌握函数的定义以及相应的性质，并能够熟练地进行应用。构造函数就是从一道数学问题所特有的地方构造出一个相对应的函数作为解题的辅助工具，通过运用函数灵活的性质，比如单调性﹑奇偶性﹑对称性等来解决数学问题。

下面我们先对一个简单的构造函数法进行讲解：已知函数f(x)，g(x)在区间[a,b]上可导，并且f’(x)＞g’(x)，则当a＜x＜b时，两个函数之间会存在什么样的关系？这样的数学题往往会以选择题的形式来进行考查，学生们通常会赋予函数一个具体的解析式，然后再根据选项进行筛选，但是这样学生们不能了解这道题的意义所在，我们可以运用构造函数法来进行解决。我们可以根据相关的条件来构造出这样的一个函数：在定义域上是一个增函数。最终解决这道数学例题。学生们在构造函数的时候，要注意到定义域和相关等式的符号，然后再利用函数的相关性质进行解题。下面我们简单介绍一下在数学方程中运用函数思想：已知关于x的方程x2-2cosx+a=0只有一解，求a的值。对于这个数学方程，我们可以将等式的左边构造成一个函数，转变成求唯一解的问题，然后对函数进行求导，从而解答。然而由于这个方程中存在一个三角函数，所以求导也很难进行解答，经过思考我们会发现，这个函数是一个偶函数，其图象关于y轴对称，这样我们就能根据函数的相关性质快速得到方程的解。通过教师们对题目的详细分析，让学生们掌握问题分析的技巧和思维，将这种思维的方式迁移到其他问题的分析中，进一步提高学生们的迁移能力。

通过以上学习迁移理论在高中数学教学中的实践运用分析，让学生们掌握数学知识之间的本质关系，将数学解题思维迁移到其他题目中或者迁移到其他科目的学习中，进而帮助学生们高效学习高中知识。

book=13,ebook=15