五阶常微分方程的Petrov-Galerkin谱元法
王金平, 庄清渠
(华侨大学 数学科学学院, 福建 泉州 362021)

五阶常微分方程的Petrov-Galerkin谱元法
王金平, 庄清渠
(华侨大学 数学科学学院, 福建 泉州 362021)
通过区间剖分,降低数值逼近多项式的阶数,构造满足试探函数空间和检验函数空间的基函数,使得离散问题所对应的线性系统的系数矩阵是稀疏的,并可以进行有效地求解.数值算例验证了五阶常微分方程的Petrov-Galerkin谱元法的有效性和高精度.
五阶常微分方程; Petrov-Galerkin谱元法; 基函数; 数值实验
谱方法作为数值求解微分方程的方法之一,已被广泛应用于自然科学和工程技术问题的数值计算[1-7].近二十年来,奇数次高阶微分方程基于谱方法的数值模拟也受到不少科研工作者的关注[8-13].由于奇次高阶微分方程的高阶项缺少对称性,若使用配置点法求解奇次高阶微分方程边值问题,如果不能选取恰当的配置点或采用高阶多项式进行逼近,容易导致条件数比较高,造成计算不稳定[10].吴胜等[13]提出Legendre-Petrov-Galerkin谱元法对三阶微分方程进行求解.由于将计算区间进行剖分,在每个区间上不需要使用太高的多项式阶数,将问题分解成一系列子问题后再用Schur补过程进行求解,计算稳定,且具有高精度.本文研究五阶常微分方程的Petrov-Galerkin谱元逼近,主要考虑方程的数值计算.
1 Petrov-Galerkin谱元法
记Λ=(-1,1),设α和β为正常数.考虑五阶常微分齐次边值问题,即
首先,将区间Λ剖分成K(K≥2)个子区间
Λk=(ak-1,ak),k=1,2,…,K.
上式中:-1=a0 定义区间Λk到参考区间Λ的坐标变换为 ∀x∈Λk. 定义分片多项式空间为 PN;K(Λ)∶={u;u|Λk∈PN(Λk),k=1,2,…,K}, 上式中:PN为Λk上次数不超过N的全体多项式组成的空间. 用N表示离散参数(N,K).定义试探函数空间和检验函数空间为 VN={u;u|Λ∈PN,K(Λ);u∈C1(Λ),u(±1)=ux(±1)=ux,x(1)=0}, WN={u;u|Λ∈PN+1,K(Λ);u∈C2(Λ),u(±1)=ux(±1)=ux,x(±1)=0}. 则问题(1)的Petrov-Galerkin谱元逼近形式为找uN∈VN, 使得 ∀vN∈WN. (2) 为了方便表达,将式(2)记为α(uN,vN)=(f,vN),记 定义 则可以验证 当k=1,2,…,K-1时,令 而且有 }. 将文献[13]求解三阶微分方程的Petrov-Galerkin谱元方法的逼近过程推广到式(2)的计算中,详细计算过程包括如下4个步骤. ∀ ∀ 步骤4 由式(7),(8)可得 ∀vN∈WN. (9) 问题(2)被分解成两套子区间问题(6),(7)及Schur补问题(8).因此,可以大大提高计算效率. (αAk-βBk+Ck)Uk=Fk,k=1,2,…,K. 上式中: 由Legendre多项式的正交性可知 j=i+5, j=i+4, j=i+3, j=i+2, j=i+1, j=i, j=i-1, j=i-2, j=i-3, j=i-4, j=i-5, j=i-6, 其他. j=i+1, j=i, j=i-1, j=i-2, j=i-3, 其他. j=i-1, 其他. 例1 问题(1)在x∈(-1,1)上的解析解为 u(x)=(x-1)2sin2mπx. 取计算参数α=β=m=1.在半log尺度下,h=1/2时,L2-误差ε及H1-误差随多项式阶数N的变化情况,如图1(a)所示.由图1(a)可知:误差随N呈指数收敛,这说明对于解析解,数值解具有谱收敛性质.在log-log尺度下,N=8时,L2-误差及H1-误差随h的变化情况,如图1(b)所示.由图1(b)可知:误差关于h呈代数衰减. (a) 误差随N的变化情况 (b) 误差随h的变化情况图1 误差分别随N和h的变化图Fig.1 Errors as a function of N and h respectively 例2 考虑变系数五阶齐次边值问题,即 此时,问题的Petrov-Galerkin谱元逼近形式为找uN∈VN, 使得 ∀vN∈WN. (10) 该问题同样可采用第1节提出的计算过程进行快速计算.但由于α(x),β(x)的存在,弱形式中前两个积分项一般不可精确计算,因此,采用Gauss-Lobatto数值积分公式替代. 取α(x)=x,β(x)=sin 10x,γ=1,u(x)=sin3πx进行计算.在半log尺度下,h=1/2时,误差随多项式阶数N的变化情况,如图2(a)所示.在log-log尺度下,N=8时,误差随h的变化情况,如图2(b)所示.由图2可知:误差随N呈指数收敛,误差随h呈代数收敛,收敛性质跟常系数方程的计算结果类似.从而说明Petrov-Galerkin谱元逼近法对求解一些变系数五阶常微分方程也是有效的. (a) 误差随N的变化情况 (b) 误差随h的变化情况图2 依赖于N和h的误差变化Fig.2 Errors as a function corresponding to N and h respectively 利用Petrov-Galerkin谱元法对五阶常微分方程进行求解.首先,通过区间剖分,将变分问题转化为一系列子问题;然后,构造恰当的试探函数和检验函数,由此得到稀疏的线性系统再进行求解.数值算例说明Petrov-Galerkin谱元逼近法对一些常系数、变系数的五阶常微分方程都是有效的,且具有高精度. [1] GOTTLIEB D,ORSZAG S A.Numerical analysis of spectral methods: Theory and applications[M].Philadelphia:SIAM,1977:1-179. [2] BERNARDI C,MADAY Y.Approximations spectrales de probl`emes aux limites elliptiques[M].Berlin:Springer-Verlag,1992:1-248. [3] GUO Benyu.Spectral methods and their applications[M].Singapore:World Scientific,1998:100-358. [4] KARNIADAKIS G,SHERWIN S J.Spectral/hp element methods for computational fluid dynamics[M].London:Oxford University Press,2005:187-348. [5] SHEN Jie,TANG Tao.Spectral and high-order methods with applications[M].Beijing:Science Press of China,2006:183-298. [6] CANUTO C,HUSSAINI M Y,QUARTERONI A,etal.Spectral methods: Fundamentals in single domains[M].Berlin:Springer-Verlag,2006:401-470. [7] CANUTO C,HUSSAINI M Y,QUARTERONI A,etal.Spectral methods: Evolution to complex geometries and applications to fluid dynamics[M].Berlin:Springer Verlag,2007:237-357. [8] MA Heping,SUN Weiwei.A Legendre-Petrov-Galerkin and chebyshev collocation method for third-order differential equations[J].SIAM J NUMER ANAL,2000,38(5):1425-1438. [9] MA Heping,SUN Weiwei.Optimal error estiamtes of the Legendre-Petrov-Galerkin method for the Korteweg-De Vries equation[J].SIAM J NUMER ANAL,2001,39(4):1380-1394. [10] SHEN Jie.A new dual-Petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation[J].SIAM J NUMER ANAL,2003,41(5):1595-1619. [11] SHEN Jie,WANG Lilian.Laguerre and composite Legendre-Laguerre dual-Petrov-Galerkin methods for third-order equations[J].Discrete and Continuous Dynamical Systems Series B,2006,6(6):1381-1402. [12] ZHENG Chunxiong,WEN Xin,HAN Houde.Numerical solution to a linearized KDV equation on unbounded domain[J].Numerical Methods for Partial Differential Equations,2008,24(2):383-399. [13] 吴胜,庄清渠.三阶微分方程的Legendre-Petrov-Galerkin谱元方法[J].华侨大学学报(自然科学版),2013,34(3):344-348. (责任编辑: 陈志贤 英文审校: 黄心中) Petrov-Galerkin Spectral-Element Method for Solving Fifth-Order Ordinary Differential Equations WANG Jinping, ZHUANG Qingqu (School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China) The polynomial order in the numerical approximation is reduced by partitioning the interval into several subintervals, and appropriate basis functions of the trial and test spaces are constructed. Which leads to a linear system with sparse coefficient matrix. Then, an efficient computational process is introduced to solve the linear system.Numerical experiment results demonstrate the high accuracy and effectiveness to the Petrov-Galerkin spectral-element method. Keywords:fifth-order ordinary differential equation; Petrov-Galerkin spectral-element method; basis functions; numerical experiments 10.11830/ISSN.1000-5013.201703027 2016-01-17 庄清渠(1980-),男,副教授,博士,主要从事微分方程数值解法的研究.E-mail:qqzhuang@hqu.edu.cn. 国家自然科学基金资助项目(11501224); 华侨大学中青年教师科研提升资助计划(ZQN-PY201); 华侨大学研究生科研创新能力培育计划项目(1400213008) O 241.8 A 1000-5013(2017)03-0435-06


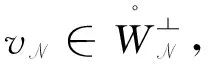

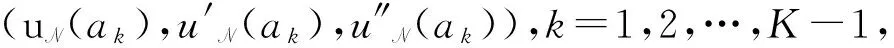
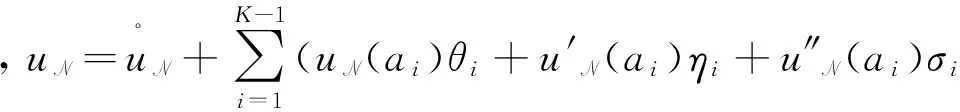

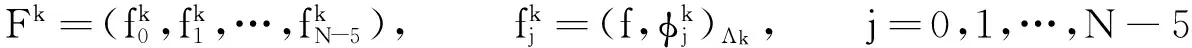


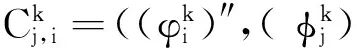
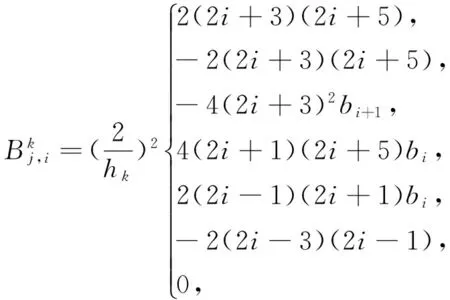


2 数值实验


3 结束语

